Analytische Geometrie

Die analytische Geometrie (auch Vektorgeometrie) ist ein Teilgebiet der Geometrie, das algebraische Hilfsmittel (vor allem aus der linearen Algebra) zur Lösung geometrischer Probleme bereitstellt. Sie ermöglicht es in vielen Fällen, geometrische Aufgabenstellungen rein rechnerisch zu lösen, ohne die Anschauung zu Hilfe zu nehmen.

Demgegenüber wird Geometrie, die ihre Sätze ohne Bezug zu einem Zahlensystem auf einer axiomatischen Grundlage begründet, als synthetische Geometrie bezeichnet.

Die Verfahren der analytischen Geometrie werden in allen Naturwissenschaften angewendet, vor allem aber in der Physik, wie zum Beispiel bei der Beschreibung von Planetenbahnen. Ursprünglich befasste sich die analytische Geometrie nur mit Fragestellungen der ebenen und der räumlichen (euklidischen) Geometrie. Im allgemeinen Sinn jedoch beschreibt die analytische Geometrie affine Räume beliebiger Dimension über beliebigen Körpern.

Das Koordinatensystem

Punkte und ihre Koordinaten in einem kartesischen Koordinatensystem der Ebene

Entscheidendes Hilfsmittel der analytischen Geometrie ist ein Koordinatensystem. In der Praxis verwendet man meist ein kartesisches Koordinatensystem. Für manche einfache Fragestellungen, etwa die Bestimmung von Geradenschnittpunkten, die Untersuchung von Geraden auf Parallelität oder die Berechnung von Teilverhältnissen, würde allerdings schon ein schiefwinkliges Koordinatensystem ausreichen. Unverzichtbar ist ein kartesisches Koordinatensystem, wenn Abstände oder Winkel berechnet werden sollen.

Vektoren

Viele Rechnungen der analytischen Geometrie werden durch die Methoden der Vektorrechnung vereinheitlicht und vereinfacht. Obwohl die gesamte analytische Geometrie ohne Vektoren erfunden wurde und natürlich immer noch ohne Vektoren praktiziert werden kann und umgekehrt der Vektorraum als ein abstrakt-algebraisches Konstrukt ohne geometrischen Bezug definiert werden kann, erscheint die Verwendung von Vektoren in kartesischen Koordinatensystemen so natürlich, dass „Lineare Algebra und Analytische Geometrie“ in der Sekundarstufe II und im mathematisch-physikalisch-technischen Grundstudium allgemein als ein Kurs unterrichtet werden.

Koordinaten- und Parametergleichungen

Kompliziertere geometrische Gebilde wie Geraden, Ebenen, Kreise, Kugeln werden als Punktmengen aufgefasst und durch Gleichungen beschrieben. Dabei kann es sich um Koordinatengleichungen oder um Parametergleichungen handeln.

Implizite Koordinatengleichung: Ein von den Koordinaten $(x,y,\dotsc )$ abhängiger Rechenausdruck wird gleich 0 gesetzt.; Beispiel (Gerade der Zeichenebene); $2x-3y+7=0$
Explizite Koordinatengleichung: Eine der Koordinaten wird durch die anderen ausgedrückt.; Beispiel (Ebene im Raum); $z=2x-5y+3$; Explizite Koordinatengleichungen haben den Nachteil, dass oft Fallunterscheidungen durchzuführen sind; so ist es beispielsweise; in der Ebene unmöglich, eine Parallele zur $y$ -Achse in der Form $y=mx+t$ darzustellen.
Parametergleichung: Der Ortsvektor ${\vec {x}}={\overrightarrow {OX}}$ eines beliebigen Punktes $X$ des Gebildes ist durch einen vektoriellen Rechenausdruck gegeben, der einen oder mehrere Parameter enthält.; Beispiel (Gerade im Raum): ${\vec {x}}={\begin{pmatrix}2\\-4\\-3\end{pmatrix}}+\lambda {\begin{pmatrix}-2\\0\\5\end{pmatrix}}$

Analytische Geometrie der Ebene

Punkte in der Ebene

Jeder Punkt $P$ der Ebene wird durch zwei Koordinaten beschrieben, z. B. $P(2\mid -1{,}5)$ . Die Koordinaten nennt man üblicherweise (in dieser Reihenfolge) die $x$ -Koordinate (auch: Abszisse) und die $y$ -Koordinate (auch: Ordinate). Gebräuchlich sind auch die Bezeichnungen $x_{1}$ und $x_{2}$ .

Die zusammengefassten Koordinaten von Punkten bilden im ebenen Fall geordnete Paare.

Geraden in der Ebene

Koordinatengleichung (implizit): $n_{x}x+n_{y}y+n_{0}=\,\!0$; Man spricht auch von der Normal(en)form der Geradengleichung, da der Vektor ${\begin{pmatrix}n_{x}\\n_{y}\end{pmatrix}}$ senkrecht (normal) zur Geraden steht.
Parametergleichung: ${\overrightarrow {OX}}={\overrightarrow {OA}}+\lambda {\vec {u}}$; Dabei ist ${\overrightarrow {OA}}={\vec {A}}$ der Ortsvektor eines beliebigen, aber fest gewählten Punktes der Geraden (Stützpunkt); ${\vec {u}}$ ist ein so genannter Richtungsvektor, also ein Vektor, dessen Richtung parallel zur Geraden ist.

Kurven zweiter Ordnung in der Ebene

Durch eine (implizite Koordinaten-)Gleichung zweiten Grades

Ax^{2}+By^{2}+Cxy+Dx+Ey+F=0

ist im Allgemeinen ein Kegelschnitt gegeben. Je nach den Werten der Koeffizienten kann es sich dabei um eine Ellipse (Spezialfall: Kreis), eine Parabel oder eine Hyperbel handeln.

Analytische Geometrie des euklidischen Raumes

Punkte im Raum

Jeder Punkt $P$ des Raumes ist durch drei Koordinaten bestimmt, z. B. $P=P(4\mid -0{,}5\mid -3)$ . Jedem Punkt $P$ ordnet man seinen Ortsvektor ${\overrightarrow {OP}}$ zu, das ist der Verbindungsvektor des Ursprungs des Koordinatensystems mit dem gegebenen Punkt. Seine Koordinaten entsprechen denen des Punktes $P$ , werden aber als Spaltenvektor geschrieben:

{\overrightarrow {OP}}={\begin{pmatrix}4\\-0{,}5\\-3\end{pmatrix}}

Die Koordinaten werden (in dieser Reihenfolge) als $x$ -, $y$ - und $z$ -Koordinate oder als $x_{1}$ -, $x_{2}$ - und $x_{3}$ -Koordinate bezeichnet.

Die zusammengefassten Koordinaten von Punkten bilden im räumlichen Fall 3-Tupel.

Geraden im Raum

Koordinatengleichungen: Geraden im Raum können nicht durch eine einzige Koordinatengleichung beschrieben werden. Man kann eine Gerade aber stets als Durchschnitt (Schnittmenge) zweier Ebenen auffassen und Koordinatengleichungen dieser beiden Ebenen (siehe unten) verwenden, um die Gerade eindeutig festzulegen.
Parametergleichung: ${\overrightarrow {OX}}={\overrightarrow {OA}}+\lambda {\vec {u}}$

Die Gleichung hat also dieselbe Form wie im zweidimensionalen Fall.

Ebenen im Raum

Koordinatengleichung (implizit): $n_{x}x+n_{y}y+n_{z}z+n_{0}=\,\!0$; Diesen Typ der Ebenengleichung bezeichnet man als Normal(en)form, da der Vektor ${\vec {n}}={\begin{pmatrix}n_{x}\\n_{y}\\n_{z}\end{pmatrix}}$ senkrecht (normal) zur Ebene steht.
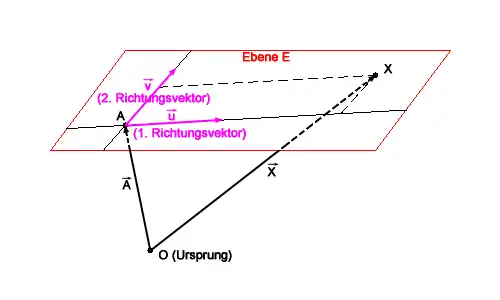
Parametergleichung: ${\overrightarrow {OX}}={\overrightarrow {OA}}+\lambda {\vec {u}}+\mu {\vec {v}}$; ${\overrightarrow {OA}}={\vec {A}}$ ist der Ortsvektor eines beliebigen, aber fest gewählten Punktes der Ebene (Stützpunkt); ${\vec {u}}$ und ${\vec {v}}$ sind linear unabhängige Richtungsvektoren (oder Spannvektoren), also Vektoren parallel zur Ebene, die die Ebene „aufspannen“.

Flächen zweiter Ordnung im Raum

Die allgemeine Koordinatengleichung zweiten Grades

Ax^{2}+By^{2}+Cz^{2}+Dxy+Exz+Fyz+Gx+Hy+Iz+J=0

beschreibt eine Fläche zweiter Ordnung. Die wichtigsten Spezialfälle sind:

Ellipsoid, elliptisches Paraboloid, hyperbolisches Paraboloid, einschaliges Hyperboloid, zweischaliges Hyperboloid, Kegel, elliptischer Zylinder, parabolischer Zylinder, hyperbolischer Zylinder.

Verallgemeinerung: Analytische Geometrie eines beliebigen affinen Raumes

Die Konzepte der analytischen Geometrie lassen sich dadurch verallgemeinern, dass man Koordinaten aus einem beliebigen Körper sowie beliebige Dimensionen zulässt.

Ist $V$ ein Vektorraum über einem Körper $K$ und $R$ ein zu $V$ gehöriger affiner Raum, so lässt sich ein $k$ -dimensionaler Unterraum von $R$ beschreiben durch die Parametergleichung

{\overrightarrow {OX}}={\overrightarrow {OA}}+\lambda _{1}{\vec {v_{1}}}+\dotsb +\lambda _{k}{\vec {v_{k}}}

.

Dabei ist ${\overrightarrow {OA}}={\vec {A}}$ der Ortsvektor eines beliebigen, aber festgewählten Punktes des Unterraumes (Stützpunkt); die Vektoren ${\vec {v_{1}}},\dotsc ,{\vec {v_{k}}}$ sind linear unabhängige Vektoren, also eine Basis des Untervektorraums von $V$ , der zum betrachteten Unterraum von $R$ gehört.

Für $k=1$ handelt es sich um die Gleichung einer Geraden, für $k=2$ um die Gleichung einer Ebene. Ist $k$ um 1 kleiner als die Dimension von $R$ bzw. $V$ , so spricht man von einer Hyperebene.

In Analogie zu den Kurven zweiter Ordnung (Kegelschnitten) der ebenen Geometrie und zu den Flächen zweiter Ordnung der räumlichen Geometrie betrachtet man im $n$ -dimensionalen affinen Raum auch so genannte Quadriken, das sind Hyperflächen zweiter Ordnung (mit der Dimension $n-1$ ), die durch Koordinatengleichungen zweiten Grades definiert sind:

\sum _{i=1}^{n}\sum _{j=1}^{n}A_{ij}x_{i}x_{j}+\sum _{i=1}^{n}B_{i}x_{i}+C=0

Typische Aufgabenstellungen der analytischen Geometrie

Inzidenz-Überprüfung

Hier geht es darum festzustellen, ob ein gegebener Punkt zu einer gegebenen Punktmenge (etwa zu einer Geraden) gehört.

Im zweidimensionalen Raum

Als Beispiel soll die Gerade mit der expliziten Koordinatengleichung

y=2\cdot x-3

betrachtet werden.

Der Punkt $P(2|1)$ liegt auf dieser Geraden, wie man durch Einsetzen der Koordinaten $x=2$ und $y=1$ (Punktprobe) erkennt:

1=2\cdot 2-3

Der Punkt $S(4|2)$ hingegen liegt nicht auf der Geraden. Für $x=4$ und $y=2$ gilt nämlich

2\neq 2\cdot 4-3

.

Im dreidimensionalen Raum

Es soll geprüft werden, ob der Punkt $Q(-1\mid 9\mid -2)$ auf der Geraden mit folgender Parameterform liegt:

{\vec {x}}={\begin{pmatrix}-7\\7\\-6\end{pmatrix}}+t{\begin{pmatrix}3\\1\\2\end{pmatrix}}

.

Wird für ${\vec {x}}$ der Ortsvektor ${\overrightarrow {OQ}}$ von $Q$ eingesetzt, so führt das zu folgenden 3 Gleichungen:

{\begin{matrix}-1&=&-7&+&t\cdot 3&\Rightarrow &t=2\\9&=&7&+&t\cdot 1&\Rightarrow &t=2\\-2&=&-6&+&t\cdot 2&\Rightarrow &t=2\\\end{matrix}}

Da $t$ in allen drei Fällen denselben Wert hat (hier $2$ ), liegt $Q$ auf der Geraden.

Bestimmung der Schnittmenge zweier Punktmengen

Die Bestimmung der Schnittmenge zweier Punktmengen (z. B. des Schnittpunkts zweier Geraden) läuft auf das Lösen eines Gleichungssystems hinaus. Je nachdem, in welcher Form die beiden Punktmengen beschrieben werden, variiert das Verfahren ein wenig:

Fall 1: Beide Punktmengen sind durch Koordinatengleichungen gegeben.; In diesem Fall wird die Schnittmenge durch die Gesamtheit der Koordinatengleichungen beschrieben.
Fall 2: Beide Punktmengen sind durch Parametergleichungen gegeben.; Die Schnittmenge erhält man durch Gleichsetzen der rechten Seiten dieser Gleichungen.
Fall 3: Eine der Punktmengen ist durch eine Koordinatengleichung gegeben, die andere durch eine Parametergleichung.; In diesem Fall setzt man die einzelnen Koordinaten der vektoriellen Parametergleichung in die Vektorgleichung ein.

Im zweidimensionalen Raum

Es soll geprüft werden, ob und wo sich die Graphen der Funktionen $g(x)$ und $f(x)$ schneiden. Dabei entspricht $g(x)=2x^{2}-2$ und $f(x)=2x+2$ :

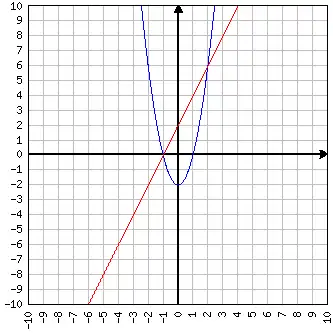
Um die Schnittpunkte zu berechnen, werden nun die Funktionsterme der Gleichungen der beiden Funktionen gleichgesetzt. Auf diese Weise findet man die $x$ -Koordinate(n), für welche die beiden Funktionen die gleiche $y$ -Koordinate haben:

{\begin{matrix}2x^{2}&-&2&=&2\cdot x&+&2\\2x^{2}&-&2\cdot x&-&4&=&0\\x^{2}&-&x&-&2&=&0\\\end{matrix}}

Das Lösen dieser quadratischen Funktion führt zu den Lösungen: $x_{1}=-1$ und $x_{2}=2$ .

Durch Einsetzung in eine der beiden anfänglichen Gleichungen ergibt das die Schnittpunkte bei: $S_{1}(-1|0)$ und $S_{2}(2|6)$ .

Im dreidimensionalen Raum

Es soll geprüft werden, ob und in welchem Punkt sich die beiden Geraden $g_{1}$ und $g_{2}$ schneiden. Die beiden Geraden seien definiert wie folgt:

g_{1}:\;{\vec {x}}={\begin{pmatrix}20\\-30\\1200\\\end{pmatrix}}+s\cdot {\begin{pmatrix}-100\\225\\-3\\\end{pmatrix}}\qquad \left(s\in \mathbb {R} \right)

g_{2}:\;{\vec {x}}={\begin{pmatrix}-2480\\105\\1167\\\end{pmatrix}}+t\cdot {\begin{pmatrix}150\\120\\1\\\end{pmatrix}}\qquad \left(t\in \mathbb {R} \right)

Wie im zweidimensionalen Raum werden auch hier die beiden Gleichungen gleichgesetzt:

{\begin{pmatrix}20\\-30\\1200\\\end{pmatrix}}+s\cdot {\begin{pmatrix}-100\\225\\-3\\\end{pmatrix}}={\begin{pmatrix}-2480\\105\\1167\\\end{pmatrix}}+t\cdot {\begin{pmatrix}150\\120\\1\\\end{pmatrix}}

s\cdot {\begin{pmatrix}-100\\225\\-3\\\end{pmatrix}}-t\cdot {\begin{pmatrix}-150\\-120\\-1\\\end{pmatrix}}={\begin{pmatrix}-2500\\135\\-33\\\end{pmatrix}}

Die Vektorgleichung kann man in folgende 3 Gleichungen zerlegen:

{\begin{array}{ccccl|l}-100\cdot s&-&150\cdot t&=&-2500&\cdot 3/50\\225\cdot s&-&120\cdot t&=&135&:5\\-3\cdot s&-&1\cdot t&=&-33&\cdot (-2)\\\end{array}}\Leftrightarrow {\begin{array}{ccccl}-6\cdot s&-&9\cdot t&=&-150\\45\cdot s&-&24\cdot t&=&27\\6\cdot s&+&2\cdot t&=&66\\\end{array}}

Addieren der ersten und letzten Gleichung liefert $-7\cdot t=-84$ bzw. $t=12$ . Aus der ersten Gleichung ergibt sich damit durch Einsetzen $-6\cdot s=-42$ , also $s=7$ . Diese Lösung erfüllt auch die zweite Gleichung, denn $45\cdot 7-24\cdot 12=27$ .

Den Ortsvektor des Schnittpunktes der Geraden erhält man, indem man einen der beiden berechneten Parameter ( $s$ ) in die entsprechende Gerade ( $g_{1}$ ) einsetzt:

{\begin{pmatrix}20\\-30\\1200\\\end{pmatrix}}+7\cdot {\begin{pmatrix}-100\\225\\-3\\\end{pmatrix}}={\begin{pmatrix}-680\\1545\\1179\\\end{pmatrix}}\Rightarrow S\left(-680|1545|1179\right)

Geschichte

Die analytische Geometrie wurde von dem französischen Mathematiker und Philosophen René Descartes begründet. Wesentliche Erweiterungen sind Leonhard Euler zu verdanken, der sich insbesondere mit den Kurven bzw. Flächen zweiter Ordnung befasste. Die Entwicklung der Vektorrechnung (unter anderem durch Hermann Graßmann) ermöglichte die heute übliche Vektorschreibweise.

David Hilbert hat nachgewiesen, dass die dreidimensionale analytische Geometrie vollständig äquivalent ist zu der (synthetischen) euklidischen Geometrie in der von ihm präzisierten Form. In praktischer Hinsicht ist sie dieser weit überlegen. In der ersten Hälfte des 20. Jahrhunderts wurde deshalb die Ansicht vertreten, Geometrie in der Art, wie sie seit Euklid gelehrt wurde, sei nur noch von geschichtlichem Interesse.

Nicolas Bourbaki ging sogar noch einen Schritt weiter: Er verzichtete ganz auf geometrische Begriffsbildungen wie Punkt, Gerade usw. und hielt mit Behandlung der Linearen Algebra alles Nötige für gesagt. Dabei wird natürlich – wie stets bei Bourbaki – von den Bedürfnissen der angewandten Mathematik völlig abgesehen.

Siehe auch

Literatur

Gerd Fischer: Analytische Geometrie: Eine Einführung für Studienanfänger. Vieweg, 2001
Wilhelm Blaschke: Analytische Geometrie. Springer, 1953

Weblinks

Wikibooks: Analytische Geometrie – Lern- und Lehrmaterialien

Ina Kersten: Analytische Geometrie und Lineare Algebra. Skript, Uni Göttingen
Joachim Gräter: Analytische Geometrie. Skript, Uni Potsdam
A. Filler: Analytische Geometrie auf spektrum.de

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.