Realer Transformator

Der reale Transformator ist ein in der Regel linearisiertes Modell eines Transformators, das den idealen Transformator um Streufelder, ohmsche Verluste, Hystereseverluste und ggf. kapazitive Effekte erweitert.

In einem realen Transformator fließt nicht der gesamte magnetische Fluss, den eine der Spulen hervorruft auch durch die andere Spule. Dieses Phänomen heißt Streuung. In vielen Anwendungsfällen ist Streuung unerwünscht, in anderen wiederum (z. B. resonante Wandler) wichtiger Bestandteil der Topologie, da mit gezielt gewählten Streufaktoren zusätzliche Spulen eingespart werden können.

Ersatzschaltbild für niedrige Frequenzen

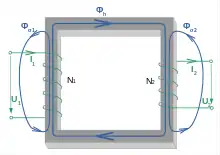
Ein realer Transformator mit Wicklungen und magnetischen Flüssen

Elektrischer und magnetischer Kreis

Die nebenstehende Abbildung wird anschaulich in folgendem Schaltplan abgebildet:

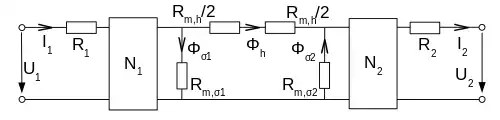
Dieser Schaltplan beinhaltet zwei elektrische Kreise und einen Magnetischen. Die Spulenwicklungen N₁ und N₂ fungieren als Kopplung zwischen elektrischem und magnetischem Kreis.

Die Streuflüsse werden im Ersatzschaltplan als magnetische Widerstände R_m,σ1 und R_m,σ2 dargestellt. Ein Strom I₁ erzeugt im magnetischen Kreis an N₁ eine Durchflutung $\Theta _{1}=N_{1}\cdot I_{1}$ , sodass ${\textstyle \Phi _{\sigma 1}={\frac {\Theta _{1}}{R_{m,\sigma 1}}}}$ . Der magnetische Widerstand R_m,h, den der Hauptfluss Φ_h erfährt, ist hier aus Symmetriegründen geteilt. In sehr guter Näherung ist R_m,h der magnetische Widerstand des Eisenjochs. Die Widerstände R₁ und R₂ repräsentieren den Widerstand der Spulenwicklungen.

Symmetrisches Ersatzschaltbild

Im nächsten Schritt wird der magnetische Kreis in die elektrischen Kreise transformiert:

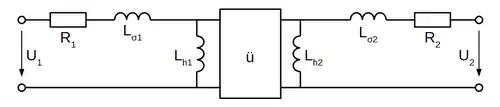
Die Spulenwicklungen N₁ und N₂ verschmelzen zu einem idealen Transformator mit Übersetzungsverhältnis ${\textstyle {\ddot {u}}={\frac {N_{1}}{N_{2}}}}$ . Bei der Transformation durch die gyratorischen Spulenkopplungen werden parallel geschaltete, magnetische Widerstände zu in Reihe geschalteten Induktivitäten: ${\textstyle L_{\sigma 1}={\frac {N_{1}^{2}}{R_{m,\sigma 1}}}}$ , ${\textstyle L_{\sigma 2}={\frac {N_{2}^{2}}{R_{m,\sigma 2}}}}$ , ${\textstyle L_{h,1}={\frac {N_{1}^{2}}{R_{m,h}/2}}}$ und ${\textstyle L_{h,2}={\frac {N_{2}^{2}}{R_{m,h}/2}}}$ .

Anmerkung: Oftmals ist auch von primärer- und sekundärer Hauptinduktivität die Rede, welche aber die Transformation beider Spulenhälften auf eine Seite meinen und daher nie im gleichen Ersatzschaltbild eingezeichnet werden dürfen![1] Dies führt oft zu Verwechslungen.

T-Ersatzschaltbild

Jedes lineare Zweitor kann als T-Ersatzschaltbild dargestellt werden. Über die oben gezeigten Schritte bekommen die einzelnen Komponenten dieses Schaltbilds hier einen direkten, realen Bezug. Der ideale Transformator wird dafür aus dem Schaltbild herausgezogen:

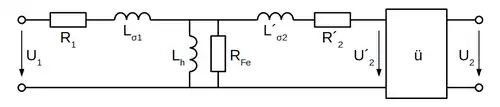
Neu hinzugekommen ist hier der Widerstand R_Fe, der die bislang nicht beachteten Hystereseverluste im Kern symbolisiert.

Bei der Transformation durch die transformatorische Kopplung [ü] bleiben Parallel-/Reihenschaltungen erhalten und es gilt: ${\textstyle L'_{\sigma 2}={\ddot {u}}^{2}\cdot L_{\sigma 2}}$ und ${\textstyle R'_{2}={\ddot {u}}^{2}\cdot R_{2}}$ Die beiden Induktivitäten L_h,1 und L_h,2 verschmelzen zur (primären) Hauptinduktivität ${\textstyle L_{h}={\frac {L_{h,1}\cdot L'_{h,2}}{L_{h,1}+L'_{h,2}}}={\frac {N_{1}^{2}}{R_{m,h}}}}$ .

Das oben gezeigte T-Ersatzschaltbild erweitert also den idealen Transformator [ü] um die realen Effekte. Das Übertragungsverhalten des realen Transformators ergibt sich durch die Verkettung des idealen- und des realen Transformators in Kettenparametern (Stromrichtung I₂ von Zweitor weg!) somit zu:

{\begin{pmatrix}U_{1}\\I_{1}\end{pmatrix}}=T_{\text{real}}\cdot {\begin{pmatrix}U_{2}\\I_{2}\end{pmatrix}}

wobei

T_{\text{real}}={\begin{pmatrix}1+{\frac {Z_{1}}{Z_{h}}}&Z_{1}+Z_{2}+{\frac {Z_{1}\cdot Z_{2}}{Z_{h}}}\\{\frac {1}{Z_{h}}}&1+{\frac {Z_{2}}{Z_{h}}}\end{pmatrix}}\cdot {\begin{pmatrix}{\ddot {u}}&0\\0&{\frac {1}{\ddot {u}}}\end{pmatrix}}

mit

{\begin{aligned}&Z_{1}=R_{1}+i\omega L_{\sigma 1}\\&Z_{2}=R'_{2}+i\omega L'_{\sigma 2}\\&Z_{h}={\frac {R_{\text{Fe}}\cdot i\omega L_{h}}{R_{\text{Fe}}+i\omega L_{h}}}\end{aligned}}

Für Schaltungsanalysen wird in aller Regel das T-Ersatzschaltbild verwendet.

Kenngrößen

Indizierung

Selbstinduktivität

Die Selbstinduktivitäten eines Transformators berechnen sich wie folgt:[2]

L_{1}={\frac {N_{1}\cdot \Phi _{11}}{I_{1}}}={\frac {N_{1}\cdot (\Lambda _{h}+\Lambda _{\sigma 1})\cdot \Theta _{1}}{I_{1}}}=N_{1}^{2}\cdot (\Lambda _{h}+\Lambda _{\sigma 1})=L_{h}+L_{\sigma 1}

L_{2}={\frac {N_{2}\cdot \Phi _{22}}{I_{2}}}={\frac {L_{h}}{{\ddot {u}}^{2}}}+L_{\sigma 2}

wobei $\Lambda ={\frac {1}{R_{m}}}$ der magnetische Leitwert und Φ₁₁ der Anteil des magnetischen Flusses ist, der vom Strom I₁ hervorgerufen wird (Superposition) und durch die Spulenwicklungen N₁ verläuft (Φ₂₂ äquivalent).

Die Selbstinduktivitäten können an den Transformatorklemmen gemessen werden, wenn die andere Seite des Transformators offen (im Leerlauf) ist. Anmerkung: Im magnetischen Kreis aus dem ersten Schaltplan wirkt N₂ wie ein Kurzschluss, wenn die Klemmen im elektrischen Kreis offen sind (gyratorische Kopplung).

Gegeninduktivität

Die Gegeninduktivitäten sind definiert als:

M_{12}={\frac {N_{1}\cdot \Phi _{12}}{I_{2}}}={\frac {N_{1}\cdot k_{2}\cdot \Phi _{22}}{I_{2}}}={\frac {N_{1}}{I_{2}}}\cdot {\frac {\Lambda _{h}}{\Lambda _{h}+\Lambda _{\sigma 2}}}\cdot (\Lambda _{h}+\Lambda _{\sigma 2})\cdot \Theta _{2}=N_{1}\cdot N_{2}\cdot \Lambda _{h}

M_{21}={\frac {N_{2}\cdot \Phi _{21}}{I_{1}}}={\frac {N_{2}\cdot k_{1}\cdot \Phi _{11}}{I_{1}}}=N_{1}\cdot N_{2}\cdot \Lambda _{h}

Wie oben gezeigt, sind die beiden Gegeninduktivitäten $M_{12}=M_{21}:=M$ im Falle linearer Materialien (wie bisher angenommen) gleich. Somit wird die Größe $M$ als Gegeninduktivität bezeichnet.

Kopplungsfaktor

Die sogenannten Flusskoppelfaktoren sind wie folgt definiert:[3]

k_{1}={\frac {\Phi _{21}}{\Phi _{11}}}={\frac {\Lambda _{h}}{\Lambda _{h}+\Lambda _{\sigma 1}}}

k_{2}={\frac {\Phi _{12}}{\Phi _{22}}}={\frac {\Lambda _{h}}{\Lambda _{h}+\Lambda _{\sigma 2}}}

$\Phi _{12}$ ist der Anteil des magnetischem Flusses durch $N_{1}$ , der von Strom $I_{2}$ hervorgerufen wird. Demnach gilt: $\Phi _{h}=\Phi _{12}+\Phi _{21}$ .

Weiter lässt sich schreiben:

k_{1}\cdot L_{1}=N_{1}^{2}\cdot \Lambda _{h}

→

\Lambda _{h}={\frac {k_{1}\cdot L_{1}}{N_{1}^{2}}}={\frac {k_{2}\cdot L_{2}}{N_{2}^{2}}}

→

\Lambda _{h}^{2}=\Lambda _{h}\cdot \Lambda _{h}=\left({\frac {k_{1}\cdot L_{1}}{N_{1}^{2}}}\right)\cdot \left({\frac {k_{2}\cdot L_{2}}{N_{2}^{2}}}\right)

→

M=N_{1}\cdot N_{2}\cdot \Lambda _{h}=N_{1}\cdot N_{2}\cdot {\sqrt {\left({\frac {k_{1}\cdot L_{1}}{N_{1}^{2}}}\right)\cdot \left({\frac {k_{2}\cdot L_{2}}{N_{2}^{2}}}\right)}}={\sqrt {k_{1}\cdot k_{2}\cdot L_{1}\cdot L_{2}}}:=k\cdot {\sqrt {L_{1}\cdot L_{2}}}

mit gemeinsamem Kopplungsfaktor $k={\sqrt {k_{1}\cdot k_{2}}}={\frac {M}{\sqrt {L_{1}\cdot L_{2}}}}$ wobei $0<k<1$ ist. Für vollkommene Kopplung ist $k=1$ .[4]

Streufaktor

Messung der Kurzschlussinduktivität

Äquivalent zum Kopplungsfaktor lassen sich Streufaktoren wie folgt definieren:

\sigma _{1}=1-k_{1}={\frac {\Lambda _{\sigma 1}}{\Lambda _{h}+\Lambda _{\sigma 1}}}={\frac {L_{\sigma 1}}{L_{1}}}

\sigma _{2}=1-k_{2}={\frac {\Lambda _{\sigma 2}}{\Lambda _{h}+\Lambda _{\sigma 2}}}={\frac {L_{\sigma 2}}{L_{2}}}

Der Faktor $\sigma =1-k^{2}=\sigma _{1}+\sigma _{2}-\sigma _{1}\cdot \sigma _{2}$ heißt Blondel-Koeffizient oder einfach Streufaktor.

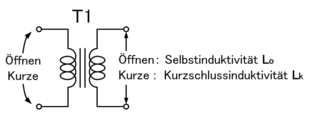
Im Falle eines symmetrischen, kapazitätsfreien Transformators ( ${\textstyle \Lambda _{\sigma 1}=\Lambda _{\sigma 2}\leftrightarrow L_{\sigma 1}=L'_{\sigma 2}\leftrightarrow \sigma _{1}=\sigma _{2}}$ ) lässt sich der Blondel-Koeffizient z. B. mit einem LCR-Meter durch Induktivitätsmessung leicht bestimmen:

\sigma =2\sigma _{1}-\sigma _{1}^{2}={\frac {L_{\mathrm {kurz} }}{L_{\mathrm {offen} }}}

wobei L_offen = L₁ die messbare Induktivität am Eingang bei offenem Ausgangs ist und L_kurz die messbare Kurzschlussinduktivität am Eingang bei Kurzschluss des Ausgangs ist (Eingang und Ausgang sind hier vertauschbar).[5]

Einzelnachweise

vgl. Dieter Zastrow: Elektrotechnik: Ein Grundlagenlehrbuch. 17. Auflage. Springer-Verlag, 2010, ISBN 978-3-8348-0562-1, Abschnitt: Realer Transformator, S. 330.
Manfred Albach: Induktivitäten in der Leistungselektronik. Springer Fachmedien Wiesbaden, Wiesbaden 2017, ISBN 978-3-658-15080-8, doi:10.1007/978-3-658-15081-5.
Praktikum Grundlagen der Elektrotechnik Versuch: Magnetischer Kreis. HTW Dresden, August 2011, abgerufen am 5. September 2015, S. 9.
Wolfgang Demtröder: Experimentalphysik 2 : Elektrizität und Optik. 5. Auflage. Springer, Berlin/Heidelberg 2009, ISBN 978-3-540-68219-6, S. 150–154.
Ing: GdE: Modelle des Transformators – Wikibooks, Sammlung freier Lehr-, Sach- und Fachbücher. In: de.wikibooks.org. Abgerufen am 4. November 2016.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] vgl. Dieter Zastrow: Elektrotechnik: Ein Grundlagenlehrbuch. 17. Auflage. Springer-Verlag, 2010, ISBN 978-3-8348-0562-1, Abschnitt: Realer Transformator, S. 330.

[2] Manfred Albach: Induktivitäten in der Leistungselektronik. Springer Fachmedien Wiesbaden, Wiesbaden 2017, ISBN 978-3-658-15080-8, doi:10.1007/978-3-658-15081-5.

[3] Praktikum Grundlagen der Elektrotechnik Versuch: Magnetischer Kreis. HTW Dresden, August 2011, abgerufen am 5. September 2015, S. 9.

[4] Wolfgang Demtröder: Experimentalphysik 2 : Elektrizität und Optik. 5. Auflage. Springer, Berlin/Heidelberg 2009, ISBN 978-3-540-68219-6, S. 150–154.

[5] Ing: GdE: Modelle des Transformators – Wikibooks, Sammlung freier Lehr-, Sach- und Fachbücher. In: de.wikibooks.org. Abgerufen am 4. November 2016.