Ferromagnetismus

Ferromagnetismus (von lateinisch Ferrum ‚Eisen‘) ist die bekannteste Art des Magnetismus von Festkörpern. Sie wird dadurch erklärt, dass die magnetischen Momente (Elementarmagnete) der Atome des Materials dazu neigen, sich parallel auszurichten. Ferromagneten erzeugen entweder selbst ein dauerhaftes Magnetfeld oder werden von einem Pol eines äußeren Magnetfelds stark angezogen. Ferromagnetische Materialien sind normalerweise Festkörper. Bekannte Anwendungen sind u. a. Dauermagnete, Elektromotoren, Transformatoren sowie die diversen Formen magnetischer Datenspeicher (Magnetband, Diskette, Festplattenlaufwerk).

Durch Ferromagnetismus wird das untere Eisenstück von einem Hufeisenmagneten angezogen.

Schematischer Verlauf der magnetischen Induktion B von ferromagnetischen (

\mu _{\mathrm {f} }

), paramagnetischen (

\mu _{\mathrm {p} }

) und diamagnetischen Materialien (

\mu _{\mathrm {d} }

) zu Vakuum (

\mu _{0}

)

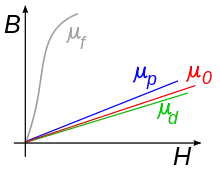
Als reine Metalle sind Eisen, Cobalt und Nickel bei Raumtemperatur (ca. 20 °C) ferromagnetisch. Bei tieferen Temperaturen sind auch einige Lanthanoide ferromagnetisch, so z. B. Gadolinium bei bis zu 19,3 °C.

Ferromagnetische Werkstoffe magnetisieren sich in einem externen Magnetfeld so, dass sich die magnetische Flussdichte in ihrem Inneren im Vergleich zum Außenraum erhöht, und werden dadurch in Richtung höherer Feldstärken („in das Magnetfeld hinein“) gezogen. Der Faktor der Flussdichteerhöhung im Vergleich zum leeren Raum wird durch die magnetische Permeabilität $\mu _{\mathrm {r} }$ (oder die magnetische Suszeptibilität $\mu _{\mathrm {r} }-1$ ) des Materials beschrieben; bei Ferromagneten gilt $\mu _{\mathrm {r} }\gg 1$ . Andere Arten der stabilen magnetischen Ordnung von Elementarmagneten sind der Antiferromagnetismus und der Ferrimagnetismus.

Eine Erhöhung der Flussdichte im Material erfolgt auch bei paramagnetischen Stoffen. Bei ihnen entsteht aber keine stabile langreichweitige Ordnung der magnetischen Momente. Daher ist der Effekt meist schwächer.

Ferromagneten zeigen die Tendenz, ihre magnetische Ordnung auch entgegen äußeren Einflüssen beizubehalten. Das führt u. a. dazu, dass sie die im Inneren erzeugte magnetische Ordnung und somit das von ihnen erzeugte äußere Magnetfeld beibehalten, auch wenn sie keinem Magnetfeld mehr ausgesetzt sind. Diese Tendenz bezeichnet man als Remanenz des Ferromagnetismus. Sie wird durch Effekte in zwei verschiedenen Größenordnungen verursacht:

mikroskopisch: die gleichgerichtete magnetische Ordnung der Elementarmagnete (z. B. der Elektronenspins, siehe unten) in atomarer Größenordnung
makroskopisch: die Anordnung der Weiss-Bezirke (sog. „Domänen“) in der Größenordnung von Mikrometern bis Nanometern

Viele Betrachtungen in der theoretischen Festkörperphysik beschränken sich auf den mikroskopischen Aspekt und bezeichnen bereits die Gleichrichtung der Elementarmagnete als Ferromagnetismus. Andererseits treten die Weiss-Bezirke auch bei anderen magnetischen Ordnungen auf.

Einführung

Typische Hysteresekurve ferromagnetischer Systeme:
Die Neukurve (erstmalige Magnetisierung!) ist in Blau, die Verläufe bei wiederholter wechselnder Magnetisierung sind in Grün dargestellt.
Die Remanenz-Magnetisierung und die Koerzitivfeldstärke (die Achsenwerte!) sind gekennzeichnet.

Ein Material wird als ein ferromagnetischer Stoff eingestuft oder deklariert, wenn sich darin unterhalb der Curie-Temperatur die magnetischen Momente der Atome parallel ausrichten. Dieser Effekt rührt daher, dass es in diesen Materialien eine Wechselwirkung zwischen den Atomen gibt, die dazu führt, dass sich die Gesamtenergie des Materials durch die Ordnung gegenüber einer ungeordneten Konfiguration verringert.

Diese Tendenz der Elementarmagnete, sich parallel auszurichten, führt zu einer spontanen Magnetisierung von größeren Bereichen, den weissschen Bezirken, in denen die Elementarmagnete größtenteils parallel ausgerichtet sind. Das unterscheidet Ferromagneten von Paramagneten, bei denen die magnetischen Momente normalerweise ungeordnet sind.

Ohne äußere Einflüsse sind die Richtungen der Magnetfelder benachbarter weissscher Bezirke antikorreliert. In den Bloch- und Neel-Wänden zwischen den Bezirken sind die Elementarmagnete so ausgerichtet, dass ein Übergang zwischen den beiden Magnetisierungsrichtungen erfolgt. In diesem Zustand erzeugt ein Körper aus einem ferromagnetischen Material kein äußeres Magnetfeld, da sich die Felder der unterschiedlichen Weiss-Bezirke gegenseitig kompensieren.

Wird das Material einem externen Magnetfeld ausgesetzt, schrumpfen die Weiss-Bezirke, die dem äußeren Magnetfeld entgegengerichtet magnetisiert sind, und klappen schließlich um. So entsteht eine makroskopische Magnetisierung, deren Feld sich so mit dem externen überlagert, dass die Feldlinien seitlich in das Material hineingezogen erscheinen. In einem inhomogenen Feld wird das so magnetisierte Material zu Orten größerer Feldstärke gezogen, seien es magnetische Nord- oder Südpole. Paramagnete verhalten sich ähnlich, allerdings erfolgt die Ausrichtung der magnetischen Momente ausschließlich aufgrund des äußeren Feldes und nicht zusätzlich durch den parallelisierenden Einfluss der benachbarten Momente. Daher ist der Effekt deutlich schwächer.

Ferromagnetische Materialien werden nach ihrem Verhalten klassifiziert, das sie zeigen, wenn sie aus einem Magnetfeld entfernt werden. Im Allgemeinen bleibt dann ein Restmagnetismus zurück, die sogenannte Remanenz.

In weichmagnetischen Materialien ist die Remanenz gering, d. h., die Magnetisierung verliert sich zum größten Teil sofort, wenn der Gegenstand wieder aus dem externen Magnetfeld entfernt wird, insbesondere, nachdem alternierende Felder angelegt wurden.
Hartmagnetische Materialien lassen sich schwerer magnetisieren, behalten aber eine größere permanente Magnetisierung. Solche Materialien, z. B. gehärteter Stahl, können zu Permanentmagneten magnetisiert werden oder von vornherein als Permanentmagnete existieren, das heißt, eine deutliche erkennbare (makroskopische) Magnetisierung dauerhaft annehmen.

Die Remanenz-Magnetisierung kann durch Anlegen eines magnetischen Gegenfeldes beseitigt werden, was bei Erreichen der Koerzitivfeldstärke geschieht. Bei hartmagnetischen Stoffen ist die Höhe des notwendigen Gegenfeldes dabei größer als bei weichmagnetischen Stoffen. Bei Permanentmagneten ist sowohl eine hohe Remanenz als auch eine hohe Koerzitivfeldstärke erwünscht.

Vom Ferromagnetismus ist der Ferrimagnetismus (z. B. in Ferriten) zu unterscheiden, der makroskopisch zwar ähnliche Eigenschaften hat, mikroskopisch aber mit dem Antiferromagnetismus verwandt ist. Bei ihm sind die Elementarmagnete jeweils wie beim Antiferromagnetismus abwechselnd entgegengesetzt gerichtet, in den zwei Richtungen jedoch unterschiedlich stark ausgeprägt, weshalb – anders als beim Antiferromagnetismus – für jedes Paar eine Magnetisierung verbleibt.

Stoffe mit ferromagnetischen Eigenschaften

Substanz	$T_{\mathrm {C} }$ in K
Co	1395
Fe	1033
Ni	627
CrO₂	390
Gd	289
Tb	219
Dy	85
EuO	70
Ho	20
Er	19

Unter den Elementen bzw. Metallen in Reinform weisen Eisen, Nickel und Cobalt bei Raumtemperatur ferromagnetische Eigenschaften auf. Als viertes Element mit ferromagnetischen Eigenschaften bei Raumtemperatur wurde 2018 Ruthenium ausgemacht (in der metastabilen raumzentrierten tetragonalen Phase).[1] Bei tieferen Temperaturen (siehe Tabelle) werden auch die Lanthanoide Gadolinium, Terbium, Dysprosium, Holmium und Erbium ferromagnetisch.

In der Praxis verwendet man häufig ferromagnetische Legierungen wie z. B. AlNiCo, SmCo, Nd₂Fe₁₄B, Ni₈₀Fe₂₀ („Permalloy“), oder NiFeCo-Legierungen („Mumetall“). Bemerkenswert ist, dass unter bestimmten Umständen auch einige Verbindungen im Allgemeinen nicht ferromagnetischer Elemente ferromagnetisches Verhalten aufweisen, beispielsweise Chromdioxid, Manganarsenid, Europium(II)-oxid oder die suprafluide A-1-Phase von He-3, ferner die sog. Heusler-Legierungen.

Ebenfalls bemerkenswert ist, dass der bekannteste ferromagnetische Stoff, Eisen, als Hauptbestandteil einer austenitischen Legierung nicht ferromagnetisch wirkt. Austenitische Gefüge sind Bestandteil vieler nichtrostender Stähle und einiger Edelstahl-Sorten. (Eisen kristallisiert bei Zimmertemperatur im kubisch-raumzentrierten Gitter. Austenitische Legierungen sind dagegen überwiegend flächenzentriert.)

Generell ist das Vorhandensein ferromagnetischer Eigenschaften davon abhängig, dass in der Elektronenkonfiguration des Grundzustandes des fraglichen Metalls oder der Verbindung ungepaarte Elektronen vorhanden sind, was im Wesentlichen nur bei Übergangsmetallen und Seltenen Erden vorkommt.

Ferromagnetismus tritt normalerweise nur im festen Aggregatzustand auf, weil die Curie-Temperatur dieser Materialien niedriger als die Schmelztemperatur ist. Ferromagnetismus wurde allerdings auch in einer unterkühlten Schmelze beobachtet.[2] Ferrofluide sind Suspensionen von festen magnetischen Teilchen in einer nichtmagnetischen Flüssigkeit.

Physikalischer Ursprung

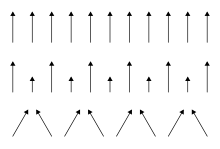
Drei Beispiele für eine ferromagnetische Ordnung einer linearen Kette magnetischer Momente

Träger der elementaren magnetischen Momente sind die Elektronenspins. Wie bei anderen kooperativen magnetischen Phänomenen ist auch beim Ferromagnetismus die magnetische Dipol-Dipol-Wechselwirkung viel zu schwach, um für die Ordnung der Spins verantwortlich zu sein. Sie hat aber, im Gegensatz zur Austauschwechselwirkung (siehe unten), sehr große Reichweite und ist deshalb trotzdem für die Anwendungen wichtig. Bei der ferromagnetischen Ordnung kommt noch hinzu, dass die parallele Ausrichtung magnetischer Momente für die Dipol-Dipol-Wechselwirkung energetisch ungünstig ist. Verantwortlich für die parallele Spinordnung des Ferromagneten ist die quantenmechanische Austauschwechselwirkung, die mit der Existenz von Singulett- und Triplett-Zuständen bei Zwei-Elektronen-Systemen zu tun hat und mit dem Pauli-Prinzip zusammenhängt. Es handelt sich also um ein nichtklassisches Phänomen, das nicht einfach zu verstehen ist:

Im Detail muss nach dem Pauli-Prinzip für eine antisymmetrische Ortswellenfunktion die zugehörige Spinwellenfunktion symmetrisch sein (z. B. bei parallelen Spins im Zwei-Elektronen-System). Man kann zeigen, dass der durchschnittliche Abstand der beiden Teilchen bei einer antisymmetrischen Ortswellenfunktion größer ist und damit für Teilchen gleicher Ladung deren Coulomb-Abstoßung geringer. Die Austauschwechselwirkung bewirkt hier also eine effektive Absenkung der potentiellen Energie. Andererseits können sich die Elektronen mit parallelem Spin nach dem Pauli-Prinzip nicht im selben Ortszustand befinden und müssen sukzessive höhere Niveaus besetzen, wodurch ihre kinetische Energie zunimmt. Die spontane Parallelstellung der Spins und damit eine ferromagnetische Ordnung wird also nur zustande kommen, wenn die Absenkung der potentiellen Energie die Erhöhung der kinetischen Energie überkompensiert. Das ist der Grund, weshalb nur die wenigen genannten Materialien ferromagnetisch sind, die breite Mehrheit aber nicht.

Eine anschauliche Darstellung hierzu gibt die Bethe-Slater-Kurve, welche die Austauschwechselwirkung in Abhängigkeit vom relativen Atomabstand zeigt, z. B. für die gängigen Metalle (Cr, Mn, Fe, Co, Ni). Der relative Atomabstand ist hierbei das Verhältnis des Atomabstandes der benachbarten Atome zum Durchmesser der nicht abgeschlossenen Elektronenschale.

In einem Satz:

Die Ordnung der magnetischen Momente wird durch die (quantenmechanische) Austauschwechselwirkung vermittelt, nicht durch (klassische) magnetische Wechselwirkung.[3]

Die magnetische Leitfähigkeit $\mu =\mu _{0}(1+\chi )$ und damit die magnetische Suszeptibilität $\chi$ ist bei Ferromagneten nicht konstant, sondern eine komplexe Funktion der angelegten Feldstärke und von der Magnetisierungs-Vorgeschichte abhängig. Meist wird daher die (differentielle) magnetische Suszeptibilität $\chi$ als Ableitung der Magnetisierung nach der Feldstärke betrachtet. Sie verschwindet im Sättigungsbereich.

Für den Zusammenhang zwischen Magnetisierung ${\vec {M}}$ und magnetischer Flussdichte ${\vec {B}}$ gilt im Übrigen die Beziehung

{\vec {B}}=\mu {\vec {H}}=\mu _{0}({\vec {H}}+\chi {\vec {H}})=\mu _{0}({\vec {H}}+{\vec {M}}).

Weiss-Bezirke, Domänen und Domänenwände

Magneto-optische Aufnahme der magnetischen Phasen, Korngeometrien und Domainorientierungen in nicht kornorientiertem Transformatorenblech (Aufnahme mit Hilfe eines magneto-optischen Sensors und Polarisationsmikroskopes)

Elektromagnetische dynamische Domänenuntersuchung von Transformatorenblech (kornorientiert)

Ferromagnetismus entsteht dadurch, dass elementare magnetische Momente eine parallele Ordnung aufweisen, die durch die Wechselwirkung der Momente untereinander auch ohne äußeres Magnetfeld bestehen bleibt. Die Bereiche gleicher Magnetisierung werden Domänen oder Weiss-Bezirke genannt. Sie treten in Größen von 0,01 µm bis 1 µm auf und sind im unmagnetisierten Zustand der Substanz nicht einheitlich orientiert.

Die Austauschwechselwirkung wirkt nur zwischen Fermionen, deren Wellenfunktionen eine wesentliche Überlappung aufweisen, in der Regel also nur zwischen nahegelegenen Teilchen. Die magnetische Wechselwirkung wirkt hingegen auch zwischen weit entfernt liegenden magnetischen Momenten. Daher übersteigt in einem ausgedehnten Ferromagneten der magnetische Energieaufwand irgendwann den Energiegewinn der Austauschwechselwirkung. Die ferromagnetische Ordnung des Festkörpers zerfällt dann in unterschiedlich orientierte Domänen. Die Bereiche des Festkörpers, in denen unterschiedlich orientierte Domänen aufeinandertreffen, heißen Domänenwand. Je nach Drehung der Magnetisierung in der Wand spricht man von Bloch-Wänden oder Néel-Wänden (bei Bloch-Wänden erfolgt die Drehung der Magnetisierung in der Senkrechten zur Wandebene; bei Néel-Wänden erfolgt sie dagegen innerhalb der Wandebene; Néel-Wände dominieren nur bei sehr dünnen magnetischen Schichten). Daneben gibt es auch andere Wand-Typen mit topologischen Singularitäten, sog. Blochlinien und Blochpunkten, die mit Änderungen des Drehverhaltens innerhalb der Wand verbunden sind. Diese Unterschiede, die sich im 10-Nanometer-Bereich bewegen können, sind subtil, aber für aktuelle Anwendungen in der Informationstechnologie interessant.

Die Ausbildung der Domänenwand erfordert die Verrichtung von Arbeit gegen die Austauschwechselwirkung; die Verkleinerung der Domänen (des Volumens einer zusammenhängenden Domäne) reduziert die magnetische Energie eines Festkörpers.

Aufgrund der nicht-kontinuierlich erfolgenden Ausrichtung der Weiss-Bezirke unter dem Einfluss äußerer Magnetfelder können sog. Barkhausen-Sprünge beobachtet werden.

Die magnetische Ordnung wird bei hohen Temperaturen aufgebrochen, die Ferromagnete sind dann nur noch paramagnetisch. Die Temperatur, oberhalb derer die ferromagnetische Ordnung verschwindet, wird als Curie-Temperatur $T_{\mathrm {C} }$ (nach Pierre Curie, dem Gatten von Marie Curie) bezeichnet. Die Suszeptibilität lässt sich oberhalb der Curie-Temperatur nach dem Curie-Weiss-Gesetz berechnen. Der Paramagnetismus bleibt für alle Temperaturen oberhalb der Curie-Temperatur erhalten, selbst nach Übergang des Festkörpers in die Flüssigkeits- oder Gasphase.

Sättigung

Magnetisierungskurven von neun ferromagnetischen Stoffen bis in den Sättigungsbereich. 1. Stahlblech, 2. Siliziumstahl, 3. Gussstahl, 4. Wolframstahl, 5. Magnetstahl, 6. Gusseisen, 7. Nickel, 8. Cobalt, 9. Magnetit

Material	Flussdichte in Tesla, bei einsetzender Sättigung
Stahl „1.3505“	0,5
Stahl „C15“	0,45
Cobalt-Eisen (Fe mit 47 bis 50 % Co)	2,35
Silicium-Eisen (Fe mit 3 bis 4 % Si)	1,5 bis 2
Nickel-Eisen (Fe mit 30 bis 50 % Ni)	1,2 bis 1,5
Ferrit (MnZn)	0,4
Ferrit (NiZn)	0,2

Bei ferromagnetischen Stoffen tritt vielfach die Sättigungsmagnetisierung in Erscheinung, ein materialspezifischer Höchstwert der Magnetisierung $M$ , der auch durch Erhöhen der äußeren magnetischen Feldstärke $H$ nicht überschritten werden kann. Die Ableitung der Magnetisierung nach der Feldstärke, die differentielle magnetische Suszeptibilität

\chi ={\frac {\partial M}{\partial H}}

,

verschwindet im Sättigungsbereich.[4]

Eine besonders gute Leitfähigkeit für den magnetischen Fluss $\Phi$ ist die wesentliche Eigenschaft vor allem ferromagnetischer Werkstoffe wie beispielsweise Weicheisen, Dynamoblech oder bestimmter Ferrite. Daher werden diese Werkstoffe verwendet, wo es auf die räumliche Führung von magnetischen Flüssen ankommt, wie bei Elektromagneten und in Eisenkernen von Transformatoren. Im Bereich der Sättigung nimmt die magnetische Leitfähigkeit stark ab. Daher ist Sättigung bei diesen technischen Anwendungen meist unerwünscht.

Trägt man für einen Werkstoff die magnetische Flussdichte $B$ gegenüber der von außen aufgebrachten magnetischen Feldstärke $H$ in einem Diagramm auf, ergibt sich die Hysteresekurve (Magnetisierungskurve). Die Abflachung der Steigung kennzeichnet dabei anschaulich den Beginn der Sättigungsmagnetisierung, man kann auch vom Erreichen der Sättigungsflussdichte bzw. der Sättigungsinduktion sprechen.

Sättigung in der Praxis

In der Geophysik werden Materialien durch Ermittlung ihrer spezifischen Curie-Temperatur identifiziert, indem man die Abhängigkeit der Sättigungsmagnetisierung von der Temperatur bestimmt.
Bei Transformatoren und Elektromotoren ist die magnetische Sättigung des Kerns unerwünscht, denn sie verringert den Wirkungsgrad und die übertragene Leistung. (Eine Ausnahme bildet der Reluktanzmotor, bei dem Sättigung eingesetzt wird, um den Leistungsfaktor zu erhöhen). Um eine Sättigung zu vermeiden, müssen magnetische Kerne in Transformatoren und Elektromotoren eine entsprechende Mindest-Querschnittsfläche aufweisen.
In magnetischen Spannungsreglern wird die Sättigung eines Transformatorkerns genutzt, um kurzzeitige Schwankungen in instabilen Stromnetzen zu stabilisieren.
Durch Einfügung eines Luftspaltes (senkrecht zum Magnetfluss) in einem geschlossenen Spulenkern lässt sich die Sättigung ferromagnetischer Kernmaterialien verhindern oder stark mindern. Allerdings sinkt die wirksame Induktivität im Vergleich zum spaltlosen Spulenkern. Angewandt wird das beispielsweise bei Drosseln. Konventionelle Vorschaltdrosseln von Gasentladungslampen sowie alle Arten von Speicherdrosseln (auch Pulverkernen) haben einen oder mehrere diskrete oder auch sogenannte (zwischen den Pulverkörnern) verteilte Luftspalte.

Hysterese

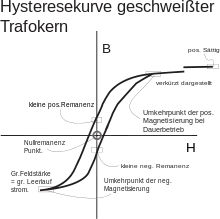
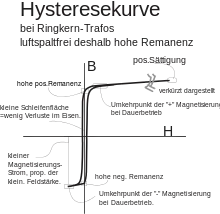
Weiche Hysteresekurve eines EI-Transformator-Eisenkerns mit Luftspalt und relativ großer koerzitiver Feldstärke

Harte Hysteresekurve eines Transformator-Eisenkernes ohne Luftspalt (Ringkern) mit kleiner koerzitiver Feldstärke

Hysterese bedeutet bei einem physikalischen System, dass dessen veränderliche Ausgangsgröße nicht allein von der Eingangsgröße abhängig ist, sondern auch von deren Verlaufsgeschichte. Ein solches Hystereseverhalten tritt bei ferromagnetischen, magnetisch leitfähigen Stoffen wie Eisen, Kobalt, Nickel und deren Legierungen auf. Erhöht man die magnetische Feldstärke $H$ in einem vorher nicht magnetisierten ferromagnetischen Stoff, erhöht sich in dessen Umgebung die magnetische Flussdichte $B$ . Verringert man die Feldstärke wieder auf 0, bleibt die magnetische Flussdichte auf einem Wert ungleich 0 stehen. Der ferromagnetische Stoff behält etwas Restmagnetismus zurück (Remanenz). Die magnetische Flussdichte hängt nicht nur von der magnetischen Feldstärke ab, sondern auch von deren zeitlichem Verlauf.

Die magnetische Flussdichte $B$ in einem ferromagnetischen Stoff wird von der Stärke des umgebenden Magnetfeldes ( $H$ ) bestimmt. Wird $H$ genügend erhöht, steigt $B$ wegen der Sättigung von $B$ nur noch sehr geringfügig an. Geht das äußere Magnetfeld zurück, so nimmt die Flussdichte wieder ab. Die magnetische Flussdichte erreicht bei dem gleichen Wert einer Feldstärke, die im Abnehmen begriffen ist, einen höheren Wert als er während des Zunehmens der Feldstärke auftrat. Wird $H$ ganz auf 0 gesenkt, geht $B$ nicht auf 0 zurück, sondern nur bis zur sogenannten Remanenz $B_{R}$ . Um die Magnetisierung wieder auf 0 zu bringen, muss daher ein entgegengesetztes Magnetfeld mit der Koerzitivfeldstärke $-H_{\mathrm {C} }$ aufgebaut werden. Da noch ein äußeres Magnetfeld anliegt, spricht man hier noch nicht von Entmagnetisierung, für die vielmehr mehrere Schritte notwendig sind. Ein erneutes Umkehren der Feldstärke von $H$ führt dazu, dass der untere Ast der Hysteresekurve durchlaufen wird. Dieser Hysteresevorgang lässt sich gut am Verlauf der Hysteresekurve oder Hystereseschleife verdeutlichen. Ein vollständiges Durchlaufen der Hysteresekurve wird als Hysteresezyklus bezeichnet. Die Hysteresekurve ist punktsymmetrisch zum Ursprung.[5] Den oberen Ast vom Umkehrpunkt der Magnetisierung durch die Remanenz als $y$ -Achsenabschnitt bis zur Koerzitivfeldstärke auf der $x$ -Achse nennt man die Entmagnetisierungskurve.[6][7] Allerdings führt nur ein in der Amplitude abklingendes magnetisches Wechselfeld durch die allmähliche Annäherung der Hysteresezyklen an den Nullpunkt zur vollständigen Entmagnetisierung ohne äußeres Magnetfeld.

Die Ursache für das Verhalten sind die sogenannten Weiss-Bezirke. Sie zeichnen sich dadurch aus, dass die Spins der Elektronen, die als Elementarmagnete aufgefasst werden können, innerhalb eines Bezirks parallel zueinander sind. Die Grenzen zwischen den Bezirken heißen Bloch-Wände.[8] Wird nun ein äußeres Magnetfeld angelegt, so wachsen die Bezirke, deren Orientierung der Ausrichtung des Magnetfeldes entspricht, auf Kosten der anderen Bezirke, indem Elektronen in den anderen Bezirken „umklappen“, sich also parallel zum Magnetfeld ausrichten. Anschaulich entspricht das einer Verschiebung der Bloch-Wände.

Störstellen, die in jedem Ferromagnetikum existieren, (in Eisen z. B. Kohlenstoffeinschlüsse) verhindern jedoch, dass das Verschieben der Bloch-Wände gleichmäßig verläuft. Wenn eine Bloch-Wand beim Verschieben auf eine Störstelle trifft, so bleibt sie zuerst an ihr hängen, und es bildet sich hinter der Störstelle eine Art Blase, in der die Spins der Elektronen noch nicht umklappen. Erst ab einer bestimmten Feldstärke schließt sich diese Blase, was zu einer plötzlichen Änderung der Magnetisierung führt. Dieser Vorgang wird Barkhausen-Sprung genannt. Durch diese ungleichmäßigen Wandverschiebungen wird eine Entmagnetisierung entlang der Neukurve unmöglich. Sie sind der Grund für das Entstehen der Hysteresekurve.
Wenn alle Elektronenspins im Ferromagnetikum an dem Feld ausgerichtet sind, ist die Sättigung erreicht. Wird nun das äußere Feld entfernt, kehren nicht alle Elektronen zur ursprünglichen Ausrichtung zurück. Die Magnetisierung sinkt bis auf das Remanenz-Niveau ab. Erst durch die Zufuhr zusätzlicher Energie kann der Stoff wieder entmagnetisiert werden. Stoffe mit hoher Remanenz sind nicht zwingend hartmagnetisch. Hartmagnetische Stoffe (Dauermagnete) benötigen eine hohe Koerzitivfeldstärke. Die Remanenz in einem Transformatorkern ist weniger vom Kernmaterial abhängig, sondern hängt stark von der Bauform des Kernes ab: Ein Ringkerntransformator-Kern hat eine sehr hohe Remanenz, weil keinerlei Luftspalte im Magnetkreis liegen. Ein Transformator mit technologisch bedingten oder absichtlich eingebauten Luftspalten hat dagegen durch Scherung (Neigung) der Hysteresekurve eine geringe Remanenz, obwohl das Kernmaterial selbst eine hohe Remanenz besitzen kann.

Typisch für die Hysterese ist das Auftreten von bistabilem Verhalten. Bei gleichen Umgebungsbedingungen ist der Zustand von der Vergangenheit, der wirkenden Spannungszeitfläche vor dem Ausschalten, abhängig. Entsprechend wird ein bestimmter Punkt im Zustandsdiagramm erreicht.

Unter Berücksichtigung der Form der Hystereseschleife kann man einen Stoff gezielt aufmagnetisieren. Entsprechende Verfahren finden Anwendung bei der Herstellung von Dauermagneten oder beim Beschreiben von magnetischen Speichermedien (Magnetband, Festplatte, Kernspeicher).

Hystereseverluste

Wenn Materialien ummagnetisiert werden, muss Energie für die Änderung der Ausrichtung der Weiss-Bezirke aufgewendet werden. Dieses Drehen verursacht Wärmeentwicklung im Material. Die Verluste sind im Allgemeinen proportional zu der Fläche innerhalb der Hysteresekurve und der Frequenz, mit der ummagnetisiert wird. Dabei ist zu beachten, dass sich die Hysteresekurve mit wachsender Frequenz gegenüber der statisch gemessenen Kurve verändert, da weitere Verlustkomponenten hinzukommen und die relative Permeabilitätszahl sinkt.

Die von der Hysteresekurve eingeschlossene Fläche entspricht der Energie pro Volumeneinheit, die im Stoff bei seiner vollständigen Ummagnetisierung in Wärme umgewandelt wird. Bei elektromagnetischen Bauteilen macht sie sich als einer der Ummagnetisierungsverlust-Komponenten bzw. als zusätzlicher Energieaufwand bemerkbar. Dieses Integral sollte im Fall von Speichermedien möglichst hoch sein. Im Fall von Kernen von Transformatoren sollte es möglichst klein sein, um nur geringe Energieverluste zu verursachen.

Magnetisch harte und weiche Materialien

Im Falle hoher Koerzitivfeldstärken spricht man von magnetisch hartem Material, da zu ihrer Neuorientierung hohe Feldstärken benötigt werden. Bei Speichermedien entspricht dies einer hohen Datensicherheit, da die geschriebenen Informationen nicht durch zufällige Streufelder umorientiert werden. Bei geringen Koerzitivfeldstärken spricht man dagegen von magnetisch weichem Material. Die Bezeichnungen rühren daher, dass reines (also weiches) Eisen im Vergleich zu magnetischen Stählen eher weichmagnetisch ist. Sehr weichmagnetisch ist das oben erwähnte Permalloy, Ni₈₀Fe₂₀. Durch Zulegieren von 5 % Molybdän erhält man das extrem weichmagnetische Supermalloy, mit dem man Räume so abschirmt, dass man die extrem schwachen Magnetfelder von Hirnströmen messen kann. Sehr weichmagnetisch sind auch die sog. metallischen Gläser auf Eisen- oder Kobaltbasis, amorphe Legierungen, die in der Struktur flüssigen Metall-Legierungen nahe dem Schmelzpunkt ähneln.

Praxisbezüge der Hysterese

Der Verlauf und die Form einer Hysteresekurve wird außer durch grundlegende Materialeigenschaften auch durch eine möglicherweise vorliegende Textur (Kornorientierung im Vergleich zum Feldlinienverlauf) oder auch einen Luftspalt beeinflusst.
ein magnetisch weiches Material kann durch plastische Verformung (Bearbeitungsprozess) hartmagnetisch oder sogar dauermagnetisch werden. Abhilfe schafft Glühen.
Bei den früher üblichen Kernspeichern der Computer wurden Ringkerne, die häufig ihren Zustand wechselten, warm und reagierten anders auf die Stromimpulse als solche, die selten angesprochen wurden. Abhilfe war entweder eine forcierte Luftkühlung, damit alle Kerne möglichst gleiche Temperatur hatten, oder ein Regime zur gleichmäßigeren Benutzung der Kerne.
In vielen Anwendungen werden kleine Hysteresezyklen um Punkte in der $B$ - $H$ -Fläche gefahren; siehe auch Kleinsignalverhalten. Aufgrund der von der Magnetisierung abhängigen Permeabilität kann die wirksame Permeabilität abweichen.
die Hysterese ist beispielsweise für die Aufnahme auf Tonband grundlegend, verursacht jedoch bei Audioaufnahmen Verzerrungen (siehe Vormagnetisierung).
Für die Auslegung und Berechnung von Transformatoren hinsichtlich Verlusten ist auch das Hystereseverhalten des Kernmaterials von Bedeutung.
Wenn Materialien ummagnetisiert werden, muss Energie für die veränderte Ausrichtung der Weiss-Bezirke aufgewendet werden. Dieses Drehen verursacht Wärme im Eisen (Hystereseverluste); beispielsweise bei Induktionskochfeldern wird bei ferromagnetischen Töpfen 1/3 der Heizleistung durch Hysterese erbracht.

Anwendungen

Ferromagnetische Werkstoffe weisen eine hohe Permeabilität mit $\mu _{\mathrm {r} }\gg 1$ auf. Dadurch werden die magnetischen Feldlinien gut im Vergleich zum umgebenden Material (etwa Luft mit $\mu _{\mathrm {r} }\approx 1$ ) geleitet. Deshalb werden ferromagnetische Werkstoffe für die Kerne von Elektromagneten und Transformatoren verwendet.

Aufgrund der hohen Permeabilitätszahl können Spulen und Drosseln für Filter oder zur Strombegrenzung kleiner gebaut werden.

Weitere Anwendungen sind Speichermedien, die den GMR-Effekt und den magnetischen Tunnelwiderstand (TMR) ausnutzen (Schreib-/Leseköpfe bei magnetischen Festplatten). Dafür wurde 2007 der Physik-Nobelpreis vergeben (Peter Grünberg und Albert Fert).

Siehe auch

Literatur

Horst Stöcker: Taschenbuch der Physik. 4. Auflage. Verlag Harry Deutsch, Frankfurt am Main 2000, ISBN 3-8171-1628-4.
Hans Fischer: Werkstoffe in der Elektrotechnik. 2. Auflage. Carl Hanser Verlag, München/Wien 1982, ISBN 3-446-13553-7.
Günter Springer: Fachkunde Elektrotechnik. 18. Auflage. Verlag Europa-Lehrmittel, Wuppertal 1989, ISBN 3-8085-3018-9.
Richard P. Feynman, Robert B. Leighton, Matthew Sands: Vorlesungen über Physik, Band 2. 3. Auflage. Oldenbourg Verlag, München/Wien 2001, ISBN 3-486-25589-4.
Charles Kittel: Introduction to Solid State Physics. 1. Ausgabe 1953 bis 14. Ausgabe 2005, ISBN 0-471-41526-X (dt.: Einführung in die Festkörperphysik. Oldenbourg, ISBN 3-486-57723-9), siehe besonders das Kapitel über Magnetismus.

Einzelnachweise und Fußnoten

P. Quarterman J.-P. Wang u. a., Demonstration of Ru as the 4th ferromagnetic element at room temperature, Nature Communications, Band 9, 2018, Artikel Nr. 2058
D. Platzek, C. Notthoff u. a.: Liquid metal undercooled below its Curie temperature. In: Applied Physics Letters. 65, 1994, S. 1723. doi:10.1063/1.112898.
Die Unmöglichkeit einer klassischen Erklärung des Ferromagnetismus wurde (unabhängig voneinander!) bereits 1911 bzw. 1921 von Niels Bohr bzw. Hendryka Johanna van Leeuwen in ihren jeweiligen Dissertationen bewiesen, veröffentlicht in:
Niels Bohr: Studier over Metallernes Elektrontheori. Københavns Universitet, 1911.
Hendrika Johanna van Leeuwen: Problèmes de la théorie électronique du magnétisme. In: Journal de Physique et le Radium. 1921, Band. 2, Nr. 12, S. 361.
Siehe auch den Artikel Bohr-van-Leeuwen-Theorem. Eine erste quantenmechanische Erklärung des Phänomens, das sog. Heisenberg-Modell, wurde erst 1928 von Werner Heisenberg gegeben.
Genau genommen gibt es bei starkem Magnetfeld noch eine kaum beobachtbare, sehr schwache Zunahme der Magnetisierung, den sog. „magnetischen Para-Effekt“, $\Delta M\propto {\sqrt {\,H}}$ , siehe:
H. Kronmüller, S. Parkin (Hrsg.): Handbook of Magnetism and Advanced Magnetic Materials. Wiley, 2007, ISBN 978-0-470-02217-7.
Wachstum, Mikrostruktur und hartmagnetische Eigenschaften von Nd-Fe-B-Schichten. S. 13, Google Books.
Karl Schüler, Kurt Brinkmann: Dauermagnete: Werkstoffe und Anwendungen. Springer, Berlin 1970.
Lothar Michalowsky, Jürgen Schneider (Hrsg.): Magnettechnik. Vulkan, Essen 2006, ISBN 978-3-8027-2139-7.
In sehr dünnen Schichten treten stattdessen die sog. Néel-Wände auf, siehe unten.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] P. Quarterman J.-P. Wang u. a., Demonstration of Ru as the 4th ferromagnetic element at room temperature, Nature Communications, Band 9, 2018, Artikel Nr. 2058

[2] D. Platzek, C. Notthoff u. a.: Liquid metal undercooled below its Curie temperature. In: Applied Physics Letters. 65, 1994, S. 1723. doi:10.1063/1.112898.

[3] Die Unmöglichkeit einer klassischen Erklärung des Ferromagnetismus wurde (unabhängig voneinander!) bereits 1911 bzw. 1921 von Niels Bohr bzw. Hendryka Johanna van Leeuwen in ihren jeweiligen Dissertationen bewiesen, veröffentlicht in:
Niels Bohr: Studier over Metallernes Elektrontheori. Københavns Universitet, 1911.
Hendrika Johanna van Leeuwen: Problèmes de la théorie électronique du magnétisme. In: Journal de Physique et le Radium. 1921, Band. 2, Nr. 12, S. 361.
Siehe auch den Artikel Bohr-van-Leeuwen-Theorem. Eine erste quantenmechanische Erklärung des Phänomens, das sog. Heisenberg-Modell, wurde erst 1928 von Werner Heisenberg gegeben.

[4] Genau genommen gibt es bei starkem Magnetfeld noch eine kaum beobachtbare, sehr schwache Zunahme der Magnetisierung, den sog. „magnetischen Para-Effekt“, $\Delta M\propto {\sqrt {\,H}}$ , siehe:
H. Kronmüller, S. Parkin (Hrsg.): Handbook of Magnetism and Advanced Magnetic Materials. Wiley, 2007, ISBN 978-0-470-02217-7.

[5] Wachstum, Mikrostruktur und hartmagnetische Eigenschaften von Nd-Fe-B-Schichten. S. 13, Google Books.

[6] Karl Schüler, Kurt Brinkmann: Dauermagnete: Werkstoffe und Anwendungen. Springer, Berlin 1970.

[7] Lothar Michalowsky, Jürgen Schneider (Hrsg.): Magnettechnik. Vulkan, Essen 2006, ISBN 978-3-8027-2139-7.

[8] In sehr dünnen Schichten treten stattdessen die sog. Néel-Wände auf, siehe unten.