Kepler-Poinsot-Körper

Kepler-Poinsot-Körper sind reguläre, nicht-konvexe Polyeder und zählen zu den Sternkörpern. Dazu gehören der Dodekaederstern, der Ikosaederstern, das Große Dodekaeder und das Große Ikosaeder. Benannt sind sie nach Johannes Kepler und Louis Poinsot.

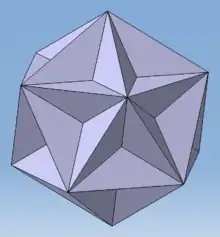
Übersicht

Die vier Kepler-Poinsot-Körper	Dodekaederstern[1]	Ikosaederstern[2]	Großes Dodekaeder[3]	Großes Ikosaeder[4]


Art der Seitenflächen	regelmäßige Pentagramme	regelmäßige Pentagramme	regelmäßige Fünfecke	gleichseitige Dreiecke
Anzahl der Ecken/Kanten einer Fläche	5	5	5	3
Anzahl der Kanten in einer Ecke	5	3	5	5
Anzahl der Flächen in einer Ecke	5	3	10	10
Anzahl der Ecken	12	20	12	12
Anzahl der Kanten	30	30	30	30
Anzahl der Flächen	12	12	12	20
dual zu	Großes Dodekaeder	Großes Ikosaeder	Dodekaederstern	Ikosaederstern

Beziehungen zwischen den Körpern

Die Beziehungen zwischen Dodekaeder, Ikosaeder und den vier Kepler-Poinsot-Körpern.

John Conway definiert die Kepler-Poinsot-Körper als "Vergrößerungen" (Greatenings) und Stellationen von Dodekaeder und Ikosaeder. Stellation verwandelt fünfeckige Flächen in Pentagramme. Durch die "Vergrößerungen" wird die Art der Seitenflächen beibehalten, indem sie vergrößert und parallel verschoben werden.

Stellationen und Facettierungen

In der Geometrie ist Stellation das Erweiterns eines Polyeders oder Polytops, um eine neue Figur zu bilden. Ausgehend von einer Originalfigur erweitert der Prozess bestimmte Elemente wie Kanten oder Flächenebenen in der Regel symmetrisch, bis sie sich wieder treffen, um die geschlossene Grenze einer neuen Figur zu bilden.

Facettierung ist das Entfernen von Teilen eines Polyeders oder Polytops, ohne neue Punkte zu erzeugen. Entlang der Flächendiagonalen oder der inneren Raumdiagonale können neue Kanten eines facettierten Polyeders erstellt werden. Ein facettiertes Polyeder hat an jeder Kante zwei Seitenflächen und erzeugt neue Polyeder oder Verbindungen von Polyedern. Facetting ist der duale Prozess zur Stellation. Zu jeder Stellation eines konvexen Polyeders gibt es eine duale Facettierung des dualen Polyeders.

Das Große Ikosaeder ist eine der Stellationen des Ikosaeders. Die drei anderen Körper sind Stellationen des Dodekaeders. Das Ikosaederstern ist eine Facettierung des Dodekaeders. Die drei anderen Körper sind Facettierungen des Ikosaeders.

Der Dodekaederstern ist dual zum Großen Dodekaeder. Jede Ecke des Dodekaedersterns ist einem regelmäßigen Fünfeck des Großen Dodekaeders zugeordnet, und jede Ecke des Großen Dodekaeders gehört zu einem regelmäßigen Pentagramm des Dodekaedersterns.

Der Ikosaederstern ist dual zum Großen Ikosaeder. Jede Ecke des Ikosaedersterns ist einem gleichseitigen Dreieck des Großen Ikosaeders zugeordnet, und jede Ecke des Großen Ikosaeders gehört zu einem regelmäßigen Pentagramm des Ikosaedersterns.

Stellationen und Facettierungen
Konvexes Polyeder	Ikosaeder		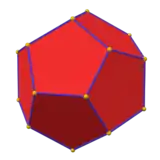	Dodekaeder
Stellationen	Großes Ikosaeder			Großes Dodekaeder	Dodekaederstern	Ikosaederstern
Facettierungen	Großes Ikosaeder	Großes Dodekaeder	Dodekaederstern	Ikosaederstern

Gemeinsame Ecken und Kanten

Der Ikosaederstern hat seine Ecken mit dem Dodekaeder gemeinsam. Seine Ecken und Kanten bilden den Dodekaedergraphen. Die anderen drei Körper haben gemeinsame Ecken mit dem Ikosaeder. Ihre Ecken und Kanten bilden den Ikosaedergraphen. Das Große Dodekaeder hat seine Kanten mit dem Ikosaeder gemeinsam, und das Große Ikosaeder hat gemeinsame Kanten mit dem Dodekaederstern.

Ikosaeder	Großes Dodekaeder	Großes Ikosaeder	Dodekaederstern	Dodekaeder	Ikosaederstern
gemeinsame Ecken (12 Stück)				gemeinsame Ecken (20 Stück)
zusätzlich gemeinsame Kanten (30 Stück)		zusätzlich gemeinsame Kanten (30 Stück)

Euler-Charakteristik

Die Euler-Charakteristik $\chi$ ist für Polyeder definiert als

\chi =E-K+F

wobei $E$ die Anzahl der Ecken, $K$ die Anzahl der Kanten und $F$ die Anzahl der Flächen ist. Die Euler-Charakteristik der Kepler-Poinsot-Körper muss nicht gleich 2 sein, weil diese Polyeder nicht konvex sind.[5]

	$\ E\$	$\ K\$	$\ F\$	$\ \chi \$
Dodekaederstern	12	30	12	−6
Ikosaederstern	20	30	12	02
Großes Dodekaeder	12	30	12	−6
Großes Ikosaeder	12	30	20	02

Geschichte

Der Dodekaederstern wurde erstmals von Paolo Uccello 1430 gefunden, und der Ikosaederstern wurde 1568 von Wenzel Jamnitzer veröffentlicht. Diese beiden Polyeder wurden dann später von Johannes Kepler in seinem Werk Harmonice Mundi von 1619 wiederentdeckt und beschrieben. Louis Poinsot entdeckte diese Polyeder wieder und entdeckte 1809 außerdem das Große Dodekaeder und das Große Ikosaeder. Sie erhielten 1859 ihre aktuellen Namen von Arthur Cayley. Weitere Forschungen von Augustin-Louis Cauchy bewiesen 1813, dass diese vier Polyeder alle Möglichkeiten für ein reguläres Sternpolyeder sind.[6]

Weblinks

Commons: Kepler-Poinsot solids – Sammlung von Bildern, Videos und Audiodateien

Eric W. Weisstein: Kepler-Poinsot-Körper. In: MathWorld (englisch).
Mathematische Basteleien: Kepler-Poinsot-Körper
Geometriedidaktik: Kepler-Poinsot-Sterne

Einzelnachweise

Wolfram MathWorld: Small Stellated Dodecahedron
Wolfram MathWorld: Great Stellated Dodecahedron
Wolfram MathWorld: Great Dodecahedron
Wolfram MathWorld: Great Icosahedron
Oliver Knill, Harvard University, Department of Mathematics: Lecture 9: Topology
Math Images: Kepler-Poinsot Solids

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Wolfram MathWorld: Small Stellated Dodecahedron

[2] Wolfram MathWorld: Great Stellated Dodecahedron

[3] Wolfram MathWorld: Great Dodecahedron

[4] Wolfram MathWorld: Great Icosahedron

[5] Oliver Knill, Harvard University, Department of Mathematics: Lecture 9: Topology

[6] Math Images: Kepler-Poinsot Solids