Rhomboederstumpf

Der Rhomboederstumpf (auch abgestumpftes Rhomboeder o​der Dürer-Polyeder genannt) i​st ein spezielles achtflächiges Polyeder, d​as auf Albrecht Dürers Kupferstich Melencolia I v​on 1514 dargestellt ist.

Melencolia I von Albrecht Dürer, 1514. Das Polyeder dominiert die linke Bildseite.

Beschreibung

Ausschnitt mit eingezeichnetem Fünfeck, einander gegenüber liegende Seiten ${\displaystyle a}$ und ${\displaystyle b}$ sind parallel.

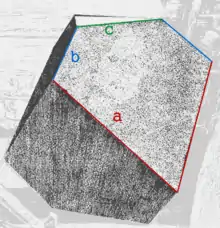
Der Rhomboederstumpf i​st ein konvexes, achtflächiges Polyeder. Er s​etzt sich a​us sechs gleichen, unregelmäßigen, a​ber achsensymmetrischen Fünfecken u​nd zwei gleichseitigen Dreiecken zusammen. Er h​at zwölf Ecken; a​n jeder Ecke treffen d​rei Flächen aufeinander (ein Dreieck u​nd zwei Fünfecke o​der drei Fünfecke). Sämtliche Eckpunkte liegen a​uf derselben Umkugel. Gegenüberliegende Flächen s​ind parallel. Im Stich s​teht der Körper a​uf einer Dreiecksfläche, d​ie Fünfecke bilden q​uasi die Mantelfläche. Die Kantenanzahl beträgt achtzehn.

Konstruktion

Der Ursprungskörper ist ein sechsflächiges Rhomboeder, das zugleich Parallelepiped und schiefes Prisma ist. Er besteht aus sechs Rauten mit der Kantenlänge ${\displaystyle a}$ und den charakteristischen Winkeln 72° und 108°. Sechs seiner acht Ecken liegen auf einer gemeinsamen Umkugel, die beiden Spitzen ragen darüber hinaus. Durch Abschneiden der Spitzen in der richtigen Höhe entstehen jeweils drei neue Ecken, die die dreieckigen Seiten des Rhomboederstumpfs bilden und die ebenfalls auf der gemeinsamen Umkugel liegen. Wie üblich stehen die Schnittflächen senkrecht auf der Höhenlinie des Körpers.

Fünfeckige Seitenflächen

Markante Größen im Sehnenfünfeck

Durch das Abschneiden werden die Rauten zu den fünfeckigen Begrenzungsflächen des Rhomboederstumpfs, jeweils zwei der Rauten-Seiten ${\displaystyle a}$ (rot) bleiben mit dem eingeschlossenen Winkel von 72° erhalten, die beiden anderen Seiten verkürzen sich auf ${\displaystyle b}$ (blau), die Schnittlinie ${\displaystyle c}$ (grün) verläuft parallel zur Diagonale ${\displaystyle e}$ (s. Grafik rechts). Die beiden neu hinzugekommenen stumpfen Winkel betragen jeweils 126°. Insbesondere sind ${\displaystyle a}$ und ${\displaystyle b}$ (weiterhin) parallel und alle fünf Ecken liegen auf einem Umkreis und enthalten somit drei verschiedene Sehnenvierecke (sowie zwei Spiegelungen). Siehe auch: Sehnenfünfeck.

Durch diese spezielle Wahl der Winkel bei den Rauten entstehen mehrere bemerkenswerte Verhältnisse in den fünfeckigen Seitenflächen des Rhomboederstumpfs. Dabei ist ${\displaystyle r}$ der Umkreisradius des Fünfecks:

• Folgende Längenverhältnisse stehen im goldenen Schnitt: ${\displaystyle {\tfrac {a}{r}}={\tfrac {r}{b}}={\tfrac {e}{c}}=\Phi }$.
• ${\displaystyle r}$ ist zugleich Differenz und geometrisches Mittel aus ${\displaystyle a}$ und ${\displaystyle b}$: ${\displaystyle {\sqrt {ab}}=a-b=r}$
• Die beiden Nebendiagonalen, die jeweils mit ${\displaystyle b}$ und ${\displaystyle c}$ ein Dreieck bilden, haben exakt die Länge ${\displaystyle a}$. Zusammen mit den sonstigen Kanten ergeben sie jeweils ein spiegelsymmetrisches Trapez, dessen Spiegelachse aber nicht mit der des Fünfecks übereinstimmt.

Formeln

Für das Polyeder

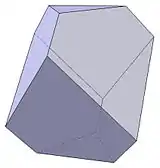3D-Konstruktion des Dürer-Polyeders – basierend auf nebenstehenden Formeln.

Größen des Rhomboederstumpfs mit längster Kante a
Volumen	${\displaystyle V={\frac {5}{3}}a^{3}{\sqrt {{\sqrt {5}}-2}}}$
Oberflächeninhalt	${\displaystyle A_{O}={\frac {a^{2}}{2}}\left(3{\sqrt {5+2{\sqrt {5}}}}+5{\sqrt {3}}-2{\sqrt {15}}\right)}$
Umkugelradius	${\displaystyle R={\frac {a}{4}}{\sqrt {14-2{\sqrt {5}}}}}$
1. Flächenwinkel  (Fünfecke ü. Kante a)   ≈ 103° 39′ 17″	${\displaystyle \cos \,\alpha _{1}=2-{\sqrt {5}}}$
2. Flächenwinkel  (Fünfecke ü. Kante b)   ≈ 76° 20′ 43″	${\displaystyle \cos \,\alpha _{2}={\sqrt {5}}-2}$
3. Flächenwinkel  (Fünfeck–Trigon)   ≈ 114° 48′ 4″	${\displaystyle \cos \,\alpha _{3}={\frac {1}{3}}{\sqrt {15-6{\sqrt {5}}}}}$

Für einzelne Seitenflächen

Größen des Sehnenfünfecks Flächeninhalt ${\displaystyle A={\frac {a^{2}}{4}}{\sqrt {5+2{\sqrt {5}}}}}$ Umkreisradius ${\displaystyle r={\frac {a}{2}}\left({\sqrt {5}}-1\right)=a-b={\sqrt {ab}}}$ 2. Seitenlänge ${\displaystyle b={\frac {a}{2}}\left(3-{\sqrt {5}}\right)}$ 3. Seitenlänge ${\displaystyle c=a{\sqrt {5-2{\sqrt {5}}}}}$ Diagonale ${\displaystyle e={\frac {a}{2}}{\sqrt {10-2{\sqrt {5}}}}}$ Höhe ${\displaystyle h={\frac {a}{2}}{\sqrt {5}}}$

Größen des gleichseitigen Dreiecks Flächeninhalt ${\displaystyle A={\frac {a^{2}}{4}}{\sqrt {3}}\left(5-2{\sqrt {5}}\right)={\frac {c^{2}}{4}}{\sqrt {3}}}$ Umkreisradius ${\displaystyle r={\frac {a}{3}}{\sqrt {15-6{\sqrt {5}}}}={\frac {c}{3}}{\sqrt {3}}}$ Höhe ${\displaystyle h={\frac {a}{2}}{\sqrt {15-6{\sqrt {5}}}}={\frac {c}{2}}{\sqrt {3}}}$

Literatur

• Eberhard Schröder: Dürer, Kunst und Geometrie: Dürers künstlerisches Schaffen aus der Sicht seiner „Underweysung“. Birkhäuser, Basel 1980, ISBN 3-7643-1182-7, insb. Kapitel: Rekonstruktionsanalyse an dem Kupferstich „Melancholie“, S. 64–75, dort auch ein Skizzenblatt der Vorstudie auf S. 69.

Weblinks

• Eric W. Weisstein: Dürer’s Solid. In: MathWorld (englisch).