Unidirektionale Schicht

Unidirektionale Schicht (kurz: UD-Schicht) ist die Bezeichnung für eine Schicht eines Faser-Kunststoff-Verbunds, in welcher alle Fasern in eine einzige Richtung orientiert sind. Die Fasern werden dabei als ideal parallel und homogen verteilt angenommen. Die unidirektionale Schicht ist transversal isotrop. Die UD-Schicht ist das Grundelement geschichteter Faser-Kunststoff-Verbunde.

Anwendung

Die UD-Schicht ist das Grundelement von geschichteten Faser-Kunststoff-Verbunden. Dies betrifft sowohl die Berechnung der elastischen Eigenschaften mit Hilfe der klassischen Laminattheorie, der Netztheorie als auch die Festigkeitsberechnung (Bruchkriterien für Faserkunststoffverbunde).

Faser-Kunststoff-Laminate werden aus elementaren UD-Schichten aufgebaut. Die jeweiligen UD-Schichten werden dabei um bestimmte Winkel verdreht, um bestimmte Eigenschaften in die jeweiligen Materialrichtungen zu erzielen.
Die unidirektionale Schicht wird in Gurten von Flügelholmen verwendet. Sie nehmen dort die Normalkräfte aus den Biegemomenten auf.
In der Wickeltechnik hergestellte Rohre oder Behälter werden aus ausgeglichenen Winkelverbunden aufgebaut. Ein ausgeglichener Winkelverbund besteht aus zwei unidirektionalen Schichten, die einen im Vorzeichen des Wickelwinkels verschiedenen Faserwinkel besitzen, z. B. ±30°.

Die UD-Schicht stellt hinsichtlich ihrer Steifigkeit und Festigkeit das Ideal einer faserverstärkten Schicht dar. Daher werden die Steifigkeits- und Festigkeitseigenschaften von UD-Schichten oft abgemindert. Insbesondere die Annahme der ideal gestreckten Faser trifft in der Realität oft nicht zu. Wellige Schichten haben aber insbesondere eine niedrige Paralleldruckfestigkeit $R_{\|}^{+}$ .

Mechanische Eigenschaften

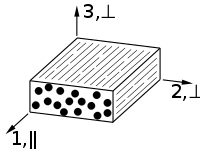
Koordinatensystem der UD-Schicht. Physikalisches System und 123-System

Die UD-Schicht ist, unabhängig vom verwendeten Faser- oder Matrixtyp, transversal isotrop. Auch UD-Schichten, die aus einer isotropen Faser (z. B. Glasfaser) bestehen, ergeben eine orthotrope Elastizität. Die transversale Isotropie ist eine Sonderform der rhombischen Anisotropie oder Orthotropie. Bei der transversalen Isotropie ist eine Symmetrieebene des Werkstoffs gegenüber der Drehung invariant. Wird die UD-Schicht außerhalb ihrer Orthotropieachsen belastet, zeigt sie anisotropes Verhalten.

Die transversale Isotropie der UD-Schicht ist durch das Fehlen der Schiebungs-Dehnungs-Kopplung, eines richtungsabhängigen Elastizitätsmoduls sowie der Invarianz gegenüber der Drehung um die Faserachse gekennzeichnet.

Indizierung

Die Beschreibung der UD-Schicht erfolgt in einem physikalischen $\|,\perp$ -Koordinatensystem, bzw. im 1,2,3-System. Dabei entspricht 1 und $\|$ der faserparallelen Richtung und 2, 3 bzw. $\perp$ der fasersenkrechten Richtung. Die Orthotropieachsen fallen mit den Koordinatenachsen zusammen.

International ist die 1,2,3-Indizierung üblich. Im englischsprachigen Raum wird jedoch oft eine andere Indizierung der Querkontraktionszahlen benutzt. Da die Querkontraktionszahlen $\nu _{\|\perp }$ und $\nu _{\perp \|}$ nicht identisch sind, kann es hier schnell zu Irrtümern kommen. Die Querkontraktionszahl $\nu _{\perp \|}$ ist stets die Kleinere von beiden. Sie wird im Englischen, um Verwechslungen vorzubeugen, minor poisson ratio genannt.

Berechnung der Grundelastizitätsgrößen

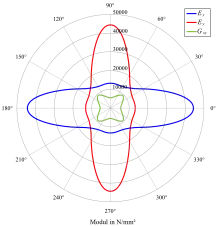
Polardiagramm der Elastizitätsmodulen einer UD-Schicht.

Die Grundelastizitätsgrößen einer UD-Schicht berechnen sich aus den Elastizitätsgrößen von Faser und Matrix auf mikromechanischer Basis. Entsprechend ihrem Faservolumenanteil gehen die Elastizitätsgrößen in die Gesamtsteifigkeit ein. Dabei wird in eine Reihenschaltung oder Parallelschaltung der Steifigkeiten unterschieden.

Die elastischen Kennwerte des orthotropen Materials lassen sich aufgrund der Symmetrie in der 2-3-Ebene reduzieren auf die E-Moduln $E_{\|}$ und $E_{\perp }$ , Schubmoduln $G_{\|\perp }$ und $G_{\perp \perp }$ und Poissonzahlen $\nu _{\|\perp }$ und $\nu _{\perp \perp }$ . Diese lassen sich unterteilen in unabhängige und abhängige Elastizitätsgrößen.

Die unabhängigen Elastizitätsgrößen sind der UD-Schicht eigen und können auf keinem anderen Weg berechnet werden. Alternativ können sie in Versuchen bestimmt werden. Dies erweist sich jedoch, besonders im Fall der Querkontraktionszahlen, als schwierig. Daher wird überwiegend der Berechnungsweg über die Mikromechanik gewählt. Um Effekte wie die Dehnungsvergrößerung zu berücksichtigen, sind eine Reihe von Korrekturen notwendig, die jedoch in der Mikromechanik berücksichtigt werden. Berechnungsverfahren können der Literatur entnommen werden.

Die abhängigen Elastizitätsgrößen werden aus den unabhängigen Elastizitätsgrößen berechnet.

Unabhängige Grundelastizitätsgrößen

Die folgenden Grundelastizitätsgrößen sind notwendig, um eine UD-Schicht vollständig zu beschreiben.

2-dimensionales Elastizitätsgesetz: $E_{\|},E_{\perp },G_{\|\perp },\nu _{\|\perp }$
3-dimensionales Elastizitätsgesetz: $E_{\|},E_{\perp },G_{\|\perp },\nu _{\|\perp },\nu _{\perp \perp }$

Anders als bei isotropen Werkstoffen lässt sich der Schubmodul $G_{\|\perp }$ nicht aus der Querkontraktionszahl berechnen. Dieser Schubmodul ist daher eine unabhängige Größe.

Der Elastizitätsmodul in faserparalleler Richtung $E_{\|}$ ist wesentlich größer als der Modul in fasersenkrechter Richtung $E_{\perp }$ . Dies ist darin begründet, dass die parallele Richtung von den steifen Fasern dominiert wird, während die senkrechte Richtung matrixdominiert ist.

Abhängige Grundelastizitätsgrößen

Aus den unabhängigen Elastizitätsgrößen können die fehlenden abhängigen Elastizitätsgrößen berechnet werden. Der Schubmodul in der transversal isotropen Ebene berechnet sich wie im Isotropen aus: $G_{\perp \perp }={\frac {E_{\perp }}{2(1+\nu _{\perp \perp })}}$ . Die zweite Querkontraktionszahl $\nu _{\perp \|}$ wird aus der Maxwell-Betti-Beziehung $\nu _{\perp \|}=\nu _{\|\perp }{\frac {E_{\perp }}{E_{\|}}}$ berechnet.

Steifigkeitsmatrix

Mit Hilfe der abhängigen und unabhängigen Elastizitätsgrößen lässt sich die Steifigkeitsmatrix für den ebenen Spannungsfall aufstellen.

${\begin{bmatrix}\displaystyle {\frac {E_{\|}}{1-\nu _{\|\perp }\nu _{\perp \|}}}&\displaystyle {\frac {\nu _{\perp \|}E_{\perp }}{1-\nu _{\|\perp }\nu _{\perp \|}}}&0\\[3ex]\displaystyle {\frac {\nu _{\|\perp }E_{\|}}{1-\nu _{\|\perp }\nu _{\perp \|}}}&\displaystyle {\frac {E_{\perp }}{1-\nu _{\|\perp }\nu _{\perp \|}}}&0\\[3ex]0&0&G_{\perp \|}\end{bmatrix}}$

Die Matrix für den räumlichen Spannungsfall ergibt sich analog.

Transformation

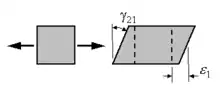
Schematische Darstellung der Dehnungs-Schiebungs-Kopplung bei Belastung außerhalb der Orthotropieachsen

Mit Hilfe der Polartransformation kann die Steifigkeitsmatrix der UD-Schicht um die 3-Achse (Achse normal zur Schichtebene) gedreht werden. Damit ist z. B. der Aufbau eines ausgeglichenen Winkelverbunds möglich. Die Polartransformation um einen Winkel $\alpha \neq {\frac {\pi }{2}},\pi ,{\frac {3\pi }{2}}\dots$ führt zur Anisotropie in der UD-Schicht und damit zur Dehnungs-Schiebungs-Kopplung.

Anwendung in der Finite-Elemente-Methode (FEM)

Die Grundelastizitätsgrößen können in allen gängigen FEM-Programmen genutzt werden, um das orthotrope bzw. anisotrope Verhalten einer UD-Schicht zu beschreiben. Es muss jedoch auf eine ausreichend feine Diskretisierung in Schichtdickenrichtung geachtet werden.

Literatur

Helmut Schürmann: Konstruieren mit Faser-Kunststoff-Verbunden. 2. Aufl. Springer, 2007.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.