Spontane Symmetriebrechung
Spontane Symmetriebrechung ist ein Konzept der theoretischen Physik, das insbesondere im Standardmodell der Elementarteilchenphysik eine wichtige Rolle spielt (Higgs-Mechanismus). Man spricht von spontaner Symmetriebrechung, wenn der Grundzustand (der Zustand niedrigster Energie) eines physikalischen Systems weniger Symmetrien aufweist als die zugrunde liegenden Bewegungsgleichungen.
Symmetrien sind wichtige physikalische Eigenschaften eines Systems, da sie zum Beispiel die Erfüllung von Erhaltungssätzen oder die Existenz von Elementarteilchen bedingen können.
Das Konzept spielt auch eine Rolle in der Festkörperphysik, wo es seinen Ursprung hat. Kühlt z. B. ein Ferromagnet unter die Curie-Temperatur ab, so entwickelt sich – auch bei beliebig schwachem internem Magnetfeld – eine in dessen Richtung orientierte „spontane Magnetisierung“, was die vorher vorhandene Drehsymmetrie bricht. Durch das schwache Magnetfeld kann also die Richtung der spontanen Magnetisierung vorgegeben werden, während der Betrag davon unabhängig ist.
Beispiel
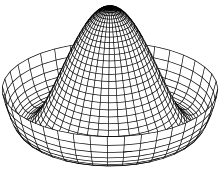
Das Bild illustriert ein rotationssymmetrisches Potential. Als mechanisches Analogon kann man sich dieses Potential als eine Fläche vorstellen, auf der eine Kugel rollt, beispielsweise den nach innen gewölbten Boden einer Flasche oder einen Sombrero. In diesem Fall hängt das Potential von zwei Ortskoordinaten und ab. In der Teilchenphysik wird statt der Ortskoordinaten ein komplexes Feld (oder auch zwei reelle Felder und ) betrachtet. Ein bestimmter Wert entspricht einer Feldkonfiguration, aus der sich Vorhersagen für im Experiment zu beobachtende Größen machen lassen. Für komplexe Felder
kann man ein solches Potential durch die Gleichung
beschreiben, wobei in der Abbildung gewählt wurde.
Dieses Potential besitzt stabile lokale Minimalwerte auf einem ganzen Kreis um die Symmetrieachse, am „Boden“ des Potentials. Im mechanischen Analogon sind dies die Orte, in denen eine Kugel ruhen kann. In der Teilchenphysik entsprechen die Minimalwerte Konfigurationen, die das Feld im Vakuum annehmen kann; man spricht daher vom „Vakuumkreis“. Die lokalen Minima und Maxima des Feldes liegen dort, wo die erste Ableitung des Potentials (der Gradient) verschwindet:
Dies ist der Fall auf dem Kreis um den Ursprung mit dem Radius :
- .
Zusätzlich gibt es einen instabilen stationären Zustand genau im Zentrum der Potentialfläche, am obersten Punkt der Wölbung. Es sei jetzt angenommen, dass sich die Kugel, bzw. das Feld, zunächst in diesem Zustand befindet. Bei der geringsten Störung wird die Kugel von diesem Punkt wegrollen und schließlich – gebremst durch Reibung – an einem Punkt auf dem Minimumskreis liegenbleiben. Analog wird das Feld aus dem instabilen Zustand (dem so genannten „falschen Vakuum“) spontan in einen stabilen Grundzustand auf dem Vakuumkreis übergehen. Die Konfiguration hat damit allerdings die Rotationssymmetrie verloren („Symmetriebrechung“), da sich das System für eine bestimmte Lage auf dem Kreis entschieden hat, die dadurch gegenüber allen anderen Lagen auf dem Kreis ausgezeichnet ist.
Konsequenzen
Die spontane Brechung globaler kontinuierlicher Symmetrien hat das Goldstonetheorem zur Folge. Dieses besagt, dass zu jedem gebrochenen Generator der Symmetriegruppe ein masseloses skalares Goldstone-Boson existiert.
Für lokale eichsymmetrische Theorien gilt das Goldstonetheorem nicht. Stattdessen gibt es dort das Phänomen des Higgs-Mechanismus, bei dem die Eichfelder mit einem skalaren Higgsfeld wechselwirken. Die Goldstone-Bosonen des spontanen Symmetriebruchs im Higgsfeld werden zu einem zusätzlichen longitudinalen Polarisationsfreiheitsgrad der Eichfelder, die dadurch eine Masse erhalten. Ohne spontane Symmetriebrechung sind die Eichfelder masselos und hätten nur zwei transversale Polarisationen (linkshändige Moden mit Spin antiparallel zur Ausbreitungsrichtung und rechtshändige Moden mit Spin parallel zur Ausbreitungsrichtung).
Nobelpreise
Yōichirō Nambu wurde für seine Idee der spontanen Symmetriebrechung der Nobelpreis für Physik 2008 zuerkannt.[1] Für den Higgs-Mechanismus erhielten François Englert und Peter Higgs 2013 den Nobelpreis für Physik.
Bedeutung für andere Sparten der Physik
Das Konzept der spontanen Symmetriebrechung spielt auch in anderen Gebieten der Physik eine wesentliche Rolle, insbesondere in der Statistischen Physik (z. B. beim kritischen Verhalten bei Phasenübergängen), in der Festkörperphysik (z. B. in der Theorie der Supraleitung) und in der Teilchenphysik (z. B. beim oben erwähnten Higgs-Mechanismus).
In der klassischen Mechanik zeigt das Konzept, dass in dieser eine meist übersehene Möglichkeit des Indeterminismus innewohnt („Kuppel-Paradox“). Das Heraufrollen eines Balls zum obersten Punkt der „Kuppel“ bzw. des „Sombreros“ (in den Zustand des labilen Gleichgewichts) mit einer kinetischen Energie, die gerade der dafür nötigen potentiellen Energie entspricht, kann – Reibungsfreiheit vorausgesetzt – zeitlich umgekehrt werden. Daher kann der Ball jederzeit spontan die Position des labilen Gleichgewichts verlassen (herabrollen) – völlig in Einklang mit den Gesetzen der klassischen Mechanik.[2] Einen – auch nur minimalen – Anstoß braucht es dazu nicht, obwohl es diesen in der Realität aufgrund der Brownschen Bewegung stets geben wird.
Weblinks
Einzelnachweise
- Scientific background on the Nobel Prize in Physics 2008: Broken Symmetries, compiled by the Class for Physics of the Royal Swedish Academy of Sciences
- Florian Freistetter: Freistetters Formelwelt: Das bizarre Kuppel-Paradox, auf: Spektrum.de vom 3. Juni 2021, zuletzt aktualisiert am 6. Juni 2021, 7 Uhr.