Populationsmodell (evolutionärer Algorithmus)
Unter der Population eines evolutionären Algorithmus (EA) versteht man die Menge aller in einer Iteration betrachteten Lösungsvorschläge des Verfahrens, welche entsprechend dem biologischen Vorbild auch Individuen genannt werden. Das Populationsmodell beschreibt die Strukturen, denen die Individuen innerhalb der Population unterliegen.
Das einfachste und vielfach bei EAs verwendete Populationsmodell ist das globale oder panmiktische Modell, das einer unstrukturierten Population entspricht. Es erlaubt jedem Individuum, ein beliebiges anderes Individuum der Population als Partner für die Erzeugung von Nachkommen zu wählen, wobei es in diesem Zusammenhang unerheblich ist, ob die Auswahl von der Fitness abhängt, zufällig erfolgt oder andere Kriterien eine Rolle spielen. Auf Grund der globalen Partnerwahl können sich bereits geringfügig bessere Individuen nach wenigen Generationen (Iteration eines EAs) in einer Population durchsetzen, sofern in dieser Phase keine besseren entstanden sind. Wenn die so gefundene Lösung nicht das gesuchte Optimum ist, spricht man von vorzeitiger Konvergenz. Dieser Effekt kann in panmiktischen Populationen öfter beobachtet werden.[1]
In der Natur sind globale Paarungspools kaum zu finden, vielmehr herrscht eine gewisse und begrenzte Isolierung durch räumliche Distanz vor. Die so entstehenden lokalen Nachbarschaften entwickeln sich zunächst unabhängig voneinander weiter und Mutanten haben eine höhere Chance sich über mehrere Generationen hinweg zu behaupten. Dadurch wird die genotypische Diversität im Genpool länger bewahrt als in einer panmiktischen Population.
Es liegt daher nahe, Unterstrukturen in die zuvor globale Population einzuführen. Dazu wurden zwei grundlegende Modelle eingeführt, die Inselmodelle, die auf einer Aufteilung der Population in feste Untermengen beruhen, welche von Zeit zu Zeit Individuen austauschen, und die Nachbarschaftsmodelle, die die Individuen sich überlappenden Nachbarschaften zuordnen.[2][3] Die damit einhergehende Aufteilung der Population legt auch eine Parallelisierung des Verfahrens nahe. Daher wird das Thema Populationsmodelle in der Literatur auch häufig im Zusammenhang mit der Parallelisierung von EAs behandelt.[4][5]
Inselmodelle
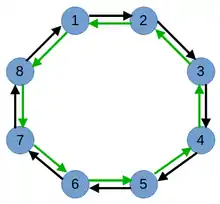
Beim Inselmodell, auch Migrationsmodell oder coarse grained model genannt, findet die Evolution in den streng aufgeteilten Teilpopulationen statt. Diese können panmiktisch organisiert sein, müssen es aber nicht. Von Zeit zu Zeit findet ein Austausch von Individuen statt, die als Migration bezeichnet wird. Die Zeit zwischen einem Austausch wird Epoche genannt und ihr Ende kann durch verschiedene Kriterien ausgelöst werden: Nach einer vorgegebenen Zeit oder vorgegebenen Anzahl ausgeführter Generationen oder nach dem Auftreten von Stagnation. Stagnation kann z. B. dadurch festgestellt werden, dass seit einer vorgegebenen Anzahl von Generationen keine Fitnessverbesserung in der Insel mehr festgestellt werden konnte. Inselmodelle führen eine Vielzahl neuer Strategieparameter ein:[2][6]
- Anzahl der Subpopulationen
- Größe der Subpopulationen
- Die Nachbarschaftsrelationen zwischen den Inseln bestimmen, welche Inseln als benachbart gelten und somit Individuen austauschen können, siehe Bild einer unidirektionalen (schwarze Pfeile) und einer bidirektionalen Ringstruktur (schwarze und grüne Pfeile).
- Kriterien für die Beendigung einer Epoche
- Migrationsrate: Anzahl oder Anteil der an der Migration beteiligten Individuen
- Migrantenauswahl: Hierzu gibt es viele Alternativen. Z. B. können die besten Individuen die schlechtesten oder zufällig gewählte ersetzen. Je nach der Migrationsrate kann das jeweils ein oder mehrere Individuen betreffen.
Nachbarschaftsmodelle
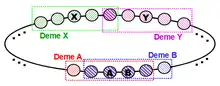
Das Nachbarschaftsmodell, auch Diffusionsmodell oder fine grained model genannt, definiert eine topologische Nachbarschaftsrelation zwischen den Individuen einer Population, die unabhängig von ihren phänotypischen Eigenschaften ist. Im einfachsten Fall ist dies die im Bild dargestellte Ringstruktur. Jedes Individuum hat eine Nachbarschaft (im Englischen deme genannt) von Individuen. Im Bild rechts sind dies beispielsweise die jeweils zwei Nachbarn zur Rechten und zur Linken des Individuums X. Zusammen mit X bilden sie das Deme von X. Jedes Deme repräsentiert eine panmiktische Teilpopulation, innerhalb derer die Partnerwahl und die Annahme von Nachkommen durch Ersetzen des Elters X erfolgt. Die Regeln für die Annahme von Nachkommen sind lokaler Natur und basieren auf der Nachbarschaft: Es kann beispielsweise festgelegt werden, dass der beste Nachkomme besser sein muss als das zu ersetzende Elter oder, weniger streng, nur besser als das schlechteste Individuum im Deme. Die erste Regel ist elitär und erzeugt einen höheren Selektionsdruck als die zweite nicht elitäre.[3] Bei elitären EAs überlebt das beste Individuum einer Population immer. Sie weichen insofern vom biologischen Vorbild ab.
Die Nachbarschaften der Individuen überlappen sich, wie im Bild beispielhaft für je zwei Nachbarschaften bestehend aus jeweils vier Nachbarn dargestellt ist. Die Demes der Individuen X und Y überlappen sich nur minimal, da beide Individuen auf dem Ring weiter voneinander entfernt sind als die Individuen A und B mit maximaler Überlappung. Die Überschneidung der Nachbarschaften bewirkt eine meist langsame Ausbreitung der genetischen Information über die Nachbarschaftsgrenzen hinweg, daher auch der Name Diffusionsmodell. Ein besserer Nachkomme braucht nun mehr Generationen als bei Panmixie, um sich in der Population auszubreiten. Dadurch wird die Herausbildung von lokalen Nischen und deren lokale Entwicklung gefördert und so die genotypische Diversität über einen längeren Zeitraum bewahrt. Das Ergebnis ist eine selbstadaptierende Balance zwischen Breiten- und Tiefensuche. Tiefensuche findet in den Nischen statt und die Breitensuche durch die Entwicklung der unterschiedlichen Nischen der gesamten Population.[3]
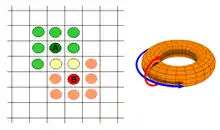
Eine Alternative zur eindimensionalen Ringstruktur ist die zweidimensionale Torusstruktur, auf der eine geschlossene Gitterstruktur aufgebracht ist, siehe rechte Seite des Bildes. Darauf basierende EAs werden auch zelluläre EAs genannt.[7] Links im Bild sind zwei sich nur gering überlappende blockförmige Nachbarschaften der Individuen A und B mit jeweils acht Nachbarn dargestellt. Beim Gitter sind mehr Nachbarschaftsfiguren möglich als beim Ring. So gibt es z. B. noch ein senkrechtes oder diagonales Kreuz oder unsymmetrische Demes. Die Ausbreitung der genetischen Information ist bei jeweils gleichen Nachbarschaftsgrößen bei langgestreckten Figuren wie einem Kreuz größer als beim Block und nochmals deutlich größer als beim Ring.[8] Beim Ring ist also der Selektionsdruck geringer als beim Torus. Das bedeutet, dass Ringnachbarschaften gut für die Erreichung einer hohen Ergebnisqualität geeignet sind, wobei vergleichsweise lange Laufzeiten in Kauf genommen werden müssen. Ist man hingegen vor allem an schnellen und guten aber möglicherweise suboptimalen Ergebnissen interessiert, so sind die Netztopologien besser geeignet.
Vergleich
Die Aufteilung einer Gesamtpopulation in Teilpopulationen verringert bei der Anwendung beider Modelle bei genetischen Algorithmen[2][3], der Evolutionsstrategie[8][9] und anderen EAs[10][11] in der Regel das Risiko vorzeitiger Konvergenz und führt insgesamt zuverlässiger und schneller zu besseren Ergebnissen als dies bei panmiktischen EAs zu erwarten wäre.
Inselmodelle haben gegenüber den Nachbarschaftsmodellen den Nachteil, dass sie eine Vielzahl neuer Strategieparameter einführen. Trotz der in der Literatur vorhandenen Untersuchungen zu diesem Thema[2][6] bleibt für den Anwender ein gewisses Risiko ungünstiger Einstellungen. Bei den Nachbarschaftsmodellen ist hingegen lediglich die Größe der Nachbarschaft vorzugeben und beim zweidimensionalen Modell kommt noch die Wahl der Nachbarschaftsfigur hinzu.
Einzelnachweise
- Yee Leung, Yong Gao, Zong-Ben Xu: Degree of population diversity – A perspective on premature convergence in genetic algorithms and its markov chain. In: IEEE Transactions on Neural Networks. Band 8, Nr. 5, 1997, S. 1165–1176, doi:10.1109/72.623217.
- Erick Cantú-Paz: Efficient and Accurate Parallel Genetic Algorithms. PhD thesis, University of Illinois, Urbana-Champaign, USA 1999.
- Martina Gorges-Schleuter: Genetic Algorithms and Population Structures - A Massively Parallel Algorithm. PhD thesis, Universität Dortmund, Fakultät für Informatik, 1990.
- Erick Cantú-Paz: A survey of parallel genetic algorithms. In: Calculateurs Paralleles. Band 10, Nr. 2, 1998, S. 141–171.
- Hatem Khalloof, Mohammad Mohammad, Shadi Shahoud, Clemens Duepmeier, Veit Hagenmeyer: A Generic Flexible and Scalable Framework for Hierarchical Parallelization of Population-Based Metaheuristics. In: Conf. Proc of the 12th Int. Conf. on Management of Digital EcoSystems (MEDES’20). 2020, S. 124–131, doi:10.1145/3415958.3433041.
- Erick Cantú-Paz: Topologies, Migration Rates, and Multi-Population Parallel Genetic Algorithms. In: Proc. of the 1st Annual Conf. on Genetic and Evolutionary Computation (GECCO). 1999, S. 91–98.
- Vahl Scott Gordon, Keith Mathias, Darrell Whitley: Cellular Genetic Algorithms as Function Optimizers: Locality Effects. In: Conf. Proc. ACM Symposium on Applied Computing (SAC’ 94). 1994, S. 237–241, doi:10.1145/326619.326732.
- Martina Gorges-Schleuter: A comparative study of global and local selection in evolution strategies. In: Parallel Problem Solving from Nature — PPSN V. Band 1498. Springer Berlin Heidelberg, Berlin, Heidelberg 1998, ISBN 978-3-540-65078-2, S. 367–377, doi:10.1007/bfb0056879 (springer.com [abgerufen am 13. Januar 2022]).
- Martina Gorges-Schleuter, Ingo Sieber, Wilfried Jakob: Local Interaction Evolution Strategies for Design Optimization. In: Conf. Proc. Congress on Evolutionary Computation (CEC 99). IEEE press, Piscataway, N.J., USA 1999, S. 2167–2174 (ieee.org [PDF]).
- Christian Blume, Wilfried Jakob: GLEAM - General Learning Evolutionary Algorithm and Method: Ein Evolutionärer Algorithmus und seine Anwendungen. In: Schriftenreihe des Instituts für Angewandte Informatik – Automatisierungstechnik. Band, Nr. 32. KIT Scientific Publishing, Karlsruhe 2009, ISBN 978-3-86644-436-2, doi:10.5445/KSP/1000013553.
- Enrique Alba Torres, Bernabé Dorronsoro, Hugo Alfonso: Cellular Memetic Algorithms. In: Journal of Computer Science and Technology. Band 5, Nr. 4, 2005, S. 257–263 (edu.ar).