Genom (evolutionärer Algorithmus)
Unter einem Genom versteht man die Menge aller Chromosomen eines Individuums, das einer Lösung einer Aufgabenstellung entspricht, welche mit einem evolutionären Algorithmus (EA) bearbeitet wird. Das Genom eines Individuums entspricht der genetischen Repräsentation einer Aufgabenstellung und ist damit ein Element des Suchraums. In diesem Zusammenhang versteht man unter einem Chromosom eine zusammenhängende Menge an Genen, wobei ein Gen aus einem oder mehreren semantisch zusammenhängenden Parametern besteht, die eine oder mehrere phänotypische Eigenschaften des Individuums bestimmen oder zumindest Einfluss darauf haben.
Zur Bewertung des Individuums muss die in seinem Genom enthaltene Information, welche auch als Genotyp bezeichnet wird, auf seinem Phänotyp abgebildet werden, welcher ein Element des Problemraums darstellt, siehe auch Hauptartikel: Genetische Repräsentation.
Häufig basiert ein Individuum auf einem einzigen Chromosom, das z. B. aus einer Kette einheitlicher Gene besteht, wobei jedes Gen z. B. ein Bit oder eine ganze oder reelle Zahl darstellt. Es gibt aber durchaus auch evolutionäre Algorithmen, die zur Lösung spezieller Aufgaben Genome verwenden, welche pro Individuum aus mehreren Chromosomen bestehen.[1][2][3]
Anforderungen an ein Genom
Der Optimierer hat bei der Gestaltung des Genoms ausgehend von der zu lösenden Aufgabenstellung eine Reihe von Freiheiten.[4][5] An ein gut geeignetes Genom sind folgende Anforderungen zu stellen:
- Erreichbarkeit aller zulässigen Punkte im Suchraum
- Gestaltung des Genoms derart, dass es nur den Suchraum und keine zusätzlichen Bereiche abdeckt, es also keine Redundanz gibt.
- Beachtung der starken Kausalität: Kleine Änderungen am Genom sollen nur zu geringen Änderungen des Phänotyps führen.[6] Dies wird auch als Lokalität der Beziehung zwischen Such- und Problemraum bezeichnet.
- Gestaltung des Genoms derart, dass es unzulässige Bereiche im Suchraum ganz oder möglichst weitgehend ausschließt.
Während die erste Anforderung unabdingbar ist, muss man sich je nach Anwendung und verwendetem EA meist nur mit einer möglichst weitgehenden Erfüllung der verbleibenden Anforderungen zufriedengeben. Es sei aber darauf hingewiesen, dass die evolutionäre Suche durch eine möglichst vollständige Erfüllung unterstützt und unter Umständen erheblich beschleunigt wird. Nissen schreibt zu dem Problem der Gestaltung eines Genoms:
„Nach Ansicht des Autors sollten sich die Lösungsrepräsentation und die Codierung möglichst direkt aus der gegebenen Problemstellung ableiten. Insbesondere sollten strukturelle Eigenheiten (Regelmäßigkeiten) des Lösungsraumes durch die Codierung erhalten bleiben, soweit sie den Suchprozeß erleichtern.“
Es besteht ein enger Zusammenhang zwischen der genetischen Repräsentation einer Aufgabenstellung und den dafür geeigneten genetischen Operatoren, darunter insbesondere Mutationen und Rekombinations- bzw. Crossoveroperatoren. Beides muss aufeinander abgestimmt sein, wobei die verwendeten Operatoren eine leichte Erreichbarkeit aller Punkte im Suchraum ermöglichen sollten.
Nachfolgend wird von Genomen ausgegangen, die jeweils aus einem Chromosom pro Individuum bestehen.
Lineare Genome
Bei linearen Genomen besteht das Chromosom aus einer Genkette, die z. B. durch ein Feld oder eine verlinkte Liste implementiert werden kann. Felder eignen sich für Anwendungen, bei denen die Position der Gene im Chromosom nicht verändert wird. Andernfalls können auch Listen von Vorteil sein.
Genome für klassische genetische Algorithmen
Die genetischen Algorithmen (GA) verwenden in ihrer klassischen Form Bitstrings und bilden die zu optimierenden Entscheidungsvariablen darauf ab. Ein Beispiel für eine boolsche und drei ganzzahlige Entscheidungsvariablen mit den Wertebereichen , und mag dies illustrieren:
| Entscheidungsvariable: | |||||||||||||||||
| Bits: | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| Position: | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
Man beachte, dass die negative Zahl hier im 2er-Komplement angegeben ist. Bei den klassischen GAs wird die Mutation für jedes Bit mit gleicher Wahrscheinlichkeit durchgeführt, was wegen der unterschiedlichen Wertigkeit der Bits dazu führt, dass kleine Änderungen große Auswirkungen auf den Phänotyp haben können. Die damit verbundene Verletzung der dritten Anforderung an Genome kann durch die Verwendung von Gray-Codes vermieden werden oder aber durch entsprechend angepasste Mutationen.
Für Aufgaben, deren Entscheidungsvariable boolesche Größen sind, ist die Codierung in Form von Bitstrings sicher eine adäquate und den Anforderungen an Genome entsprechende Darstellung. Es gab aber bereits frühzeitig Kritik an der Verwendung binärer Genome für ganzzahlige oder reellwertige Größen.[8][9][10]
Genome mit reellwertigen oder ganzzahligen Genen
Für die Bearbeitung von Aufgabenstellungen mit reellwertigen oder gemischt-ganzzahligen Entscheidungsvariablen bieten sich EAs wie die Evolutionstrategie (ES) oder die reellcodierten GAs[9][11] an. Im Falle gemischt-ganzzahliger Werte wird häufig gerundet, was aber eine gewisse Verletzung des Redundanzgebotes (2. Forderung an ein Genom) darstellt. Wenn die Genauigkeiten der reellen Werte sich sinnvoll eingrenzen lassen, kann dieser Verletzung durch die Verwendung ganzzahligcodierter EAs[12][5] abgeholfen werden. Dazu werden die gültigen Ziffern reeller Werte durch Multiplikation mit einem geeigneten Faktor auf ganze Zahlen abgebildet. Beispielsweise wird aus 12,380 durch Multiplikation mit 1000 der Integerwert 12380. Dies ist natürlich bei der Genotyp-Phänotyp-Abbildung für Bewertung und Ergebnisdarstellung zu berücksichtigen.
Für kombinatorische Probleme bietet sich die Verwendung ganzzahliger Genome an. Es empfiehlt sich, dann auch daran angepasste EAs zu verwenden, die insbesondere über geeignete Mutations- und Crossoveroperatoren verfügen.
Genome für Koevolution
Wenn ein Genom neben den Entscheidungsvariablen zusätzliche Informationen enthält, die die Evolution und/oder die Abbildung der Entscheidungsvariablen in ihrer Gesamtheit auf den Phänotyp beeinflussen und selbst der Evolution unterliegen, spricht man von Koevolution. Ein typisches Beispiel dafür ist die ES, die eine oder mehrere Mutationsschrittweiten als Strategieparamter in jedes Chromosom mit aufnimmt. Ein anderes Beispiel ist ein zusätzliches Gen zur Steuerung einer Auswahlheuristik für die Ressourcenzuordnung bei Schedulingaufgaben.[13]
Diesem Vorgehen liegt die Annahme zu Grunde, dass gute Lösungen auf einer passenden Auswahl der Strategieparameter oder auf dem Steuerungsgen, das die Genotyp-Phänotyp-Abbildung beeinflusst, beruhen. Der Erfolg der ES gibt dieser Annahme Recht.
Genom für komplexe Gene
Die oben vorgestellten Genome sind gut zur Bearbeitung von Aufgabenstellungen der kontinuierlichen, gemischt-ganzzahligen, rein ganzzahligen oder der kombinatorischen Optimierung geeignet. Bei einer Kombination dieser Optimierungsgebiete wird es hingegen je nach Aufgabenstellung schwierig, diese auf einfache Werteketten abzubilden.[4] Eine Lösung besteht darin, das bisher verwendete Genkonzept zu erweitern und ein Gen als die Beschreibung eines Elements oder einer elementaren Eigenschaft des Phänotyps anzusehen. Dazu wird ein Gentyp definiert, der so viele Parameter des jeweils passenden Datentyps enthält, wie zur Beschreibung des jeweiligen Elements des Phänotyps erforderlich sind. Ein Gen wird damit als die Beschreibung semantisch zusammengehöriger Teileigenschaften des Phänotyps begriffen. Ein Chromosom besteht nun aus Genen als Datenobjekte der Gentypen, wobei je nach Anwendung jeder Gentyp genau einmal als Gen vorkommt oder aber beliebig oft im Chromosom enthalten sein kann. Letzteres führt zu Chromosomen dynamischer Länge, wie sie für manche Aufgaben erforderlich sind.[14] Die Gentypdefinitionen können auch Angaben zu den zulässigen Wertebereichen der Genparameter enthalten, welche bei der Chromosomenerzeugung und durch geeignete Mutationen eingehalten werden, sodass keine Letalmutationen entstehen können. Implementiert wurde dieses Konzept im EA GLEAM (General Learning Evolutionary Algorithm and Method).[14][15]
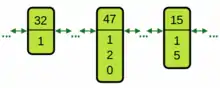
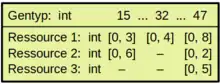
Zur Illustration soll ein Beispiel dienen, bei dem es um das Scheduling von Workflows an heterogene Ressourcen geht, wobei ein Arbeitsschritt mehrere unterschiedliche Ressourcen benötigen kann. Ein Workflow gibt vor, welche Arbeitsschritte parallel bearbeitet werden können und welche hintereinander ausgeführt werden müssen. Heterogene Ressourcen bedeuten in diesem Zusammenhang unterschiedliche Bearbeitungszeiten bei unterschiedlichen Kosten.[13][14] Jede Schedulingoperation benötigt also ein oder mehrere Parameter, die die Ressourcenauswahl bestimmen. Ein dafür geeignetes Genom sieht pro Arbeitsschritt einen Gentyp vor, der einen Parameter für jede benötigte Ressource hat, wobei die Wertebereiche der Parameter von der Anzahl der jeweils verfügbaren alternativen Ressourcen für diesen Arbeitsschritt abhängen. Der Gentyp des Arbeitsschritts 15 mit zwei Ressourcen, für die es jeweils vier bzw. sieben Alternativen gibt, sähe dann wie im linken Bild dargestellt aus. Da die Parameter Indizes in Listen der verfügbaren Ressourcen für den jeweiligen Arbeitsschritt darstellen, beginnt ihr Wertebereich bei 0. Das rechte Bild zeigt exemplarisch drei zu den Gentypen gehörige Gene eines Chromosoms in Listendarstellung. Die Genotyp-Phänotyp-Abbildung dieses Beispiels wird im Artikel Genetische Repräsentation dargestellt.
Weitere Anwendungen, deren Aufgabenstellung durch das beschriebene Gentypenmodell einfach und direkt auf ein Genom abbildbar ist, sind z. B. die im Buch über GLEAM[14] vorgestellte Roboterbahnplanung und die Designoptimierung einer Aktorplatte mit vorher nicht bekannter Komponentenanzahl.
Genome für die Genetische Programmierung
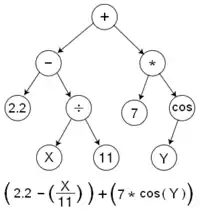
Die genetische Programmierung (GP) ist ein EA-Typ zur Erzeugung von Computerprogrammen oder Schaltkreisen. Der bei der Übersetzung eines Computerprogramms vom Compiler als interne Repräsentation erzeugte Syntaxbaum kann als eine den Anforderungen an ein Genom genügende Darstellung eines Programms angesehen werden. Nebenstehendes Bild zeigt als Beispiel den Syntaxbaum eines mathematischen Ausdrucks. Mutationsoperatoren können je nach dargestellter Syntaxstruktur Teilbäume umhängen, verändern oder löschen. Die Rekombination erfolgt durch den Austausch dafür geeigneter Teilbäume.
Einzelnachweise
- Nicholas Baine: A simple multi-chromosome genetic algorithm optimization of a Proportional-plus-Derivative Fuzzy Logic Controller. In: NAFIPS 2008 - 2008 Annual Meeting of the North American Fuzzy Information Processing Society. Mai 2008, S. 1–5, doi:10.1109/NAFIPS.2008.4531273 (ieee.org [abgerufen am 17. Februar 2022]).
- Jin Peng, Zhang Shu Chu: A Hybrid Multi-chromosome Genetic Algorithm for the Cutting Stock Problem. In: 2010 3rd International Conference on Information Management, Innovation Management and Industrial Engineering. Band 1, November 2010, S. 508–511, doi:10.1109/ICIII.2010.128 (ieee.org [abgerufen am 17. Februar 2022]).
- Rachel Cavill, Steve Smith, Andy Tyrrell: Multi-chromosomal Genetic Programming. In: Proceedings of the 2005 Conference on Genetic and Evolutionary Computation - GECCO '05. ACM Press, Washington DC, USA 2005, ISBN 978-1-59593-010-1, S. 1753–1759, doi:10.1145/1068009.1068300 (acm.org [abgerufen am 17. Februar 2022]).
- Wilfried Jakob: Applying Evolutionary Algorithms Successfully: A Guide Gained from Real-world Applications. Karlsruher Institut für Technologie (KIT), 2021, doi:10.5445/ir/1000135763, arxiv:2107.11300 (kit.edu [abgerufen am 19. Februar 2022]).
- Hartmut Pohlheim: Evolutionäre Algorithmen. Springer Berlin Heidelberg, Berlin, Heidelberg 2000, ISBN 978-3-642-63052-1, doi:10.1007/978-3-642-57137-4 (springer.com [abgerufen am 21. Februar 2022]).
- Edgar Galván-López, James McDermott, Michael O’Neill, Anthony Brabazon: Towards an Understanding of Locality in Genetic Programming. In: Conf. proc. of Genetic and Evolutionary Computation Conference (GECCO’10). ACM, New York 2010, S. 901–908, doi:10.1145/1830483.1830646.
- Volker Nissen: Evolutionäre Algorithmen. Deutscher Universitätsverlag, Wiesbaden 1994, ISBN 978-3-8244-0217-5, doi:10.1007/978-3-322-83430-0 (springer.com [abgerufen am 19. Februar 2022]).
- Darrell Whitley: A Genetic Algorithm Tutorial. In: Statistics and Computing. Band 4, Nr. 2, Juni 1994, ISSN 0960-3174, doi:10.1007/BF00175354 (springer.com [abgerufen am 21. Februar 2022]).
- Zbigniew Michalewicz: Genetic Algorithms + Data Structures = Evolution Programs. Third, revised and Extended edition Auflage. Springer Berlin Heidelberg, Berlin, Heidelberg 1996, ISBN 978-3-662-03315-9.
- F. Herrera, M. Lozano, J.L. Verdegay: Tackling Real-Coded Genetic Algorithms: Operators and Tools for Behavioural Analysis. In: Artificial Intelligence Review. Band 12, Nr. 4, 1998, S. 265–319, doi:10.1023/A:1006504901164 (springer.com [abgerufen am 20. Februar 2022]).
- Darrell Whitley: An overview of evolutionary algorithms: practical issues and common pitfalls. In: Information and Software Technology. Band 43, Nr. 14, Dezember 2001, S. 817–831, doi:10.1016/S0950-5849(01)00188-4 (elsevier.com [abgerufen am 21. Februar 2022]).
- Jean-Paul Watson, Darrell Whitley: The GENITOR Group. Colorado State University, USA, abgerufen am 21. Februar 2022.
- Wilfried Jakob, Sylvia Strack, Alexander Quinte, Günther Bengel, Karl-Uwe Stucky: Fast Rescheduling of Multiple Workflows to Constrained Heterogeneous Resources Using Multi-Criteria Memetic Computing. In: Algorithms. Band 6, Nr. 2, 22. April 2013, ISSN 1999-4893, S. 245–277, doi:10.3390/a6020245 (mdpi.com [abgerufen am 21. Februar 2022]).
- Christian Blume, Wilfried Jakob: GLEAM - General Learning Evolutionary Algorithm and Method : ein Evolutionärer Algorithmus und seine Anwendungen. KIT Scientific Publishing, 2009, doi:10.5445/ksp/1000013553 (kit.edu [abgerufen am 21. Februar 2022]).
- Wilfried Jakob: Git-Repository von GLEAM. Karlsruher Institut für Technologie, 2021, abgerufen am 23. Februar 2022 (englisch).