Endlicher Automat
Ein endlicher Automat (EA, auch Zustandsmaschine, Zustandsautomat; englisch finite state machine, FSM) ist ein Modell eines Verhaltens, bestehend aus Zuständen, Zustandsübergängen und Aktionen. Ein Automat heißt endlich, wenn die Menge der Zustände, die er annehmen kann (später S genannt), endlich ist. Ein endlicher Automat ist ein Spezialfall aus der Menge der Automaten.
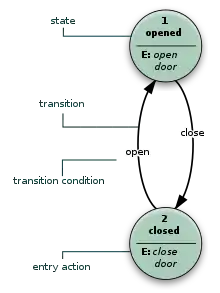
Ein Zustand kann Information über die Vergangenheit beinhalten, da das System ihn ja auf dessen bisherigem Weg erreicht hat. D. h., er reflektiert in gewissem Umfang die Änderungen der Eingabe seit dem Systemstart bis zum aktuellen Zeitpunkt.
Ein Zustandsübergang ist ein Übergang aus dem aktuellen Zustand in einen neuen (anderen) Zustand. Zu diesem Übergang kommt es, wenn die angegebenen logischen Bedingungen/„Eingaben“ vorliegen, die erfüllt sein müssen, um den Übergang zu ermöglichen.
Eine Aktion ist die „Ausgabe“ des EA, die in einer bestimmten Situation erfolgt. Es gibt vier Typen von Aktionen:
- Eingangsaktion: Die Aktion wird ausgeführt/ausgegeben beim Eintreten in einen Zustand (egal über welchen Zustandsübergang der Zustand erreicht wurde, falls es mehrere gibt).
- Ausgangsaktion: Die Aktion wird beim Verlassen eines Zustandes generiert (egal über welchen Zustandsübergang der Zustand verlassen wird).
- Eingabeaktion: Die Aktion wird abhängig vom aktuellen Zustand und der Eingabe generiert. Einem Zustand können also mehrere Aktionen zugeordnet sein, die abhängig davon ausgeführt werden, über welchen Zustandsübergang er erreicht/verlassen wird.
- Übergangsaktion: Die Aktion wird abhängig/während eines Zustandsübergangs ausgeführt.
Ein EA kann als Zustandsübergangsdiagramm wie in Abbildung 1 dargestellt werden. Zusätzlich werden mehrere Typen von Übergangstabellen (bzw. Zustandsübergangstabellen) benutzt. Die folgende Tabelle zeigt eine sehr verbreitete Form von Übergangstabellen: Die Kombination aus dem aktuellen Zustand (B) und Eingabe (Y) führt zum nächsten Zustand (C). Die komplette Information über die möglichen Aktionen wird mit Hilfe von Fußnoten angegeben. Eine Definition des EA, die auch die volle Ausgabeinformation beinhaltet, ist mit Zustandstabellen möglich, die für jeden Zustand einzeln definiert werden (siehe auch virtueller EA).
| Momentaner Zustand/ Element des Eingabealphabets | Element des Eingabealphabets 1 | Element des Eingabealphabets 2 | Element des Eingabealphabets 3 |
|---|---|---|---|
| Zustand A | … | … | … |
| Zustand B | … | Zustand C | … |
| Zustand C | … | … | … |
Die Definition des EA wurde ursprünglich in der Automatentheorie eingeführt und später in der Computertechnik übernommen.
Zustandsmaschinen werden hauptsächlich in der Entwicklung digitaler Schaltungen, Modellierung des Applikationsverhaltens (Steuerungen), generell in der Softwaretechnik sowie Wort- und Spracherkennung benutzt.
Klassifizierung
Generell werden zwei Gruppen von EA unterschieden: Akzeptoren und Transduktoren.
Akzeptoren
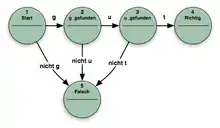
Sie akzeptieren und erkennen die Eingabe und signalisieren durch ihren Zustand das Ergebnis nach außen. In der Regel werden Symbole (Buchstaben) als Eingabe benutzt. Das Beispiel in der Abbildung 2 zeigt einen EA, der das Wort „gut“ akzeptiert. Akzeptoren werden vorwiegend in der Wort- und Spracherkennung eingesetzt.
Transduktoren (Transducer)
Transduktoren generieren Ausgaben in Abhängigkeit von Zustand und Eingabe mit Hilfe von Aktionen. Sie werden vorwiegend für Steuerungsaufgaben eingesetzt, wobei grundsätzlich zwei Typen unterschieden werden:
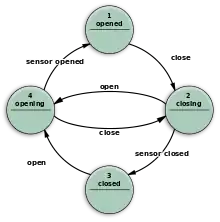
- Moore-Automat
- Im Moore-Modell werden nur Eingangsaktionen benutzt, d. h., die Ausgabe hängt nur vom Zustand ab (). Das Verhalten eines Moore-Automaten ist dadurch, verglichen mit dem Mealy-Modell, einfacher und leichter zu verstehen. Das Beispiel in Abbildung 3 zeigt einen Moore-Automaten, der eine Aufzugtür steuert. Die Zustandsmaschine kennt zwei Befehle, „aufmachen“ und „zumachen“, die von einem Benutzer eingegeben werden können. Die Eingangsaktion (E:) im Zustand „Aufgehend“ startet einen Motor, der die Tür öffnet, und die Eingangsaktion im Zustand „Zugehend“ startet den Motor in entgegengesetzter Richtung. Die Eingangsaktionen in den Zuständen „Auf“ und „Zu“ halten den Motor an. Sie signalisieren außerdem die Situation nach außen (z. B. zu anderen EA).

- Mealy-Automat
- Im Mealy-Modell werden Eingabeaktionen benutzt, d. h., die Ausgabe hängt von Zustand und Eingabe ab (). Der Einsatz von Mealy-Automaten führt oft zu einer Verringerung der Anzahl zu berücksichtigender Zustände. Die Funktion des EA ist dadurch komplexer und oft schwieriger zu verstehen. Das Beispiel in der Abbildung 4 zeigt einen Mealy-EA, der das gleiche Verhalten wie der EA im Moore-Beispiel aufweist. Dabei gibt es zwei Eingabeaktionen (I:) mit „starte den Motor, um die Tür zu schließen, wenn die Eingabe ‚zumachen‘ erfolgt“ und „starte den Motor in entgegengesetzter Richtung, um die Tür zu öffnen, wenn die Eingabe ‚aufmachen‘ erfolgt“.
Sofern das zeitliche Verhalten unberücksichtigt bleiben kann, sind Moore- und Mealy-Automaten gleichwertig. Unter dieser Voraussetzung kann der eine in den jeweils anderen überführt werden; oft werden in der Praxis Mischmodelle benutzt. Im Bereich des synchronen Systemdesigns (Digitalelektronik) dagegen gibt es wichtige Unterschiede, die nicht außer Acht gelassen werden dürfen. Diese betreffen sowohl die unterschiedliche Zahl von Zuständen als auch die zeitliche Charakteristik der generierten Kontrollsignale.[1]
Eine weitere Klassifizierung der EA wird durch die Unterscheidung zwischen deterministischen (DEA) und nicht-deterministischen (NEA) Automaten gemacht. In den deterministischen Automaten existiert für jeden Zustand genau ein Übergang für jede mögliche Eingabe. Bei den nicht-deterministischen Automaten kann es keinen oder auch mehr als einen Übergang für die mögliche Eingabe geben.
Ein EA, der nur aus einem Zustand besteht, wird als kombinatorischer EA bezeichnet. Er benutzt nur Eingabeaktionen.
Die Logik des EA
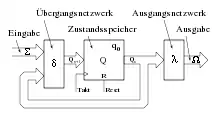
Der nächste Zustand und die Ausgabe des EA ist eine Funktion der Eingabe und des aktuellen Zustandes. Abbildung 5 zeigt den Ablauf der Logik.
Das mathematische Modell
Es gibt unterschiedliche Definitionen, je nach Typ des DEA. Ein Akzeptor ist ein 5-Tupel (), wobei:
- ist die endliche Zustandsmenge ()
- ist der Startzustand ()
- ist das endliche Eingabealphabet
- ist die Endzustandsmenge ()
- ist die Übergangsfunktion, sie lässt sich als Automatentafel oder als Zustandsübergangsgraph darstellen.
Ein Transduktor ist ein 7-Tupel (), wobei:
- ist das Eingabealphabet (eine endliche nicht leere Menge von Symbolen),
- ist das Ausgabealphabet (eine endliche nicht leere Menge von Symbolen),
- ist eine endliche nicht leere Menge von Zuständen,
- ist die Endzustandsmenge ()
- ist der Anfangszustand und ein Element aus ,
- ist die Zustandsübergangsfunktion: ,
- ist die Ausgabefunktion: ,
Falls die Ausgabefunktion eine Funktion von Zustand und Eingabealphabet ist (), dann handelt es sich um ein Mealy-Modell. Falls die Ausgabefunktion nur vom Zustand abhängt (), dann ist es ein Moore-Modell.
Optimierung
Ein EA wird optimiert, indem die Zustandsmaschine mit der geringsten Anzahl von Zuständen gefunden wird, die die gleiche Funktion erfüllt. Dieses Problem kann zum Beispiel mit Hilfe von Färbungsalgorithmen gelöst werden.
Homing-Folgen und UIO-Folgen
Homing-Folgen
Eine Homing-Folge (auch Homing-Sequenz) ist eine Folge von Eingaben, sodass sich anhand der Ausgaben bestimmen lässt, in welchem Zustand sich die Maschine danach befindet. Dadurch kann bei stark zusammenhängenden Zustandsmaschinen sehr leicht eine Folge gefunden werden, um wieder zum Initialzustand zurückzukehren, also nach Hause (englisch home). Jede minimale Zustandsmaschine besitzt eine Homing-Folge.
| Eingabe | mögliche Zustandsmengen (bei welcher Ausgabe) |
|---|---|
| ε | |
| a | |
| aa | |
| ab | |
| b |
UIO-Folgen
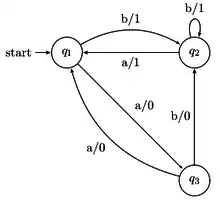
Eine UIO-Folge (Unique-Input-Output-Folge) ist eine Folge von Eingaben, um anhand der Ausgaben zu bestimmen, aus welchem Zustand man gestartet ist. Eine solche Folge existiert nicht immer, das Problem, eine zu finden, ist PSPACE-vollständig.
Beispiel UIO-Folgen zu Abb. 6:
- : a/0, a/0, b/1
- : a/1
- : b/0
Implementierung
Hardware
In digitalen Schaltungen werden EA mit Hilfe von speicherprogrammierbaren Steuerungen, logischen Gattern, Flip-Flops oder Relais gebaut. Eine Hardwareimplementation benötigt normalerweise ein Register, um die Zustandsvariable zu speichern, eine Logikeinheit, die die Zustandsübergänge bestimmt, eine zweite Logikeinheit, die für die Ausgabe verantwortlich ist, sowie einen Taktgeber oder ein Verzögerungsglied, um zwischen vorherigem, aktuellem und nachfolgendem Zustand weiterschalten/unterscheiden zu können.
Software
In der Softwareentwicklung werden meist folgende Konzepte verwendet, um Applikationen mit Hilfe von Zustandsmaschinen zu modellieren bzw. implementieren:
- Ereignisgesteuerter endlicher Automat
- Virtueller endlicher Automat
Reale Computer als EA-Server
Alle in der wirklichen Welt existenten digitalen Computer haben eine endliche Speichergröße und können somit nur eine endliche (wenn auch sehr hohe) Zahl von digitalen Schaltzuständen annehmen. Sie lassen sich daher als Teilmenge der endlichen Automaten betrachten. Jedoch ist es für theoretische Betrachtungen oft nützlicher, sie stattdessen als Teilmenge leistungsfähigerer Automatenmodelle, wie etwa der Turingmaschine, zu betrachten.
Darstellung endlicher Automaten
Die allgemeinen Regeln für das Zeichnen eines Zustandsübergangsdiagramms sind wie folgt:
- Kreise stellen Zustände dar. Im Kreis steht der Name des Zustands.
- Pfeile zwischen Zuständen stellen die Transitionen dar. Auf jedem Pfeil steht, welche Bedingungen den Übergang ermöglichen.
Siehe auch
Literatur
- John E. Hopcroft, Jeffrey Ullman: Einführung in die Automatentheorie, formale Sprachen und Komplexitätstheorie. 2. Auflage. Addison-Wesley, Bonn, München 1990, ISBN 3-89319-181-X (Originaltitel: Introduction to automata theory, languages and computation.).
- Peter Sander, Wolffried Stucky, Rudolf Herschel: Automaten, Sprachen, Berechenbarkeit. Teubner, Stuttgart 1992, ISBN 3-519-02937-5.
- Ferdinand Wagner: Modeling Software with Finite State Machines: A Practical Approach. Auerbach, Boca Raton 2006, ISBN 0-8493-8086-3.
- Zvi Kohavi: Switching and Finite Automata Theory. McGraw-Hill, New York 1978, ISBN 0-07-035310-7. (englisch)
- Arthur Gill: Introduction to the Theory of Finite-state Machines. McGraw-Hill, New York 1962. (englisch)
- Heinz-Dietrich Wuttke, Karsten Henke: Schaltsysteme – Eine automatenorientierte Einführung. Pearson Studium, München 2003, ISBN 3-8273-7035-3.
Weblinks
- Formale Sprachen und Abstrakte Automaten – Kurs von Tino Hempel
- Kara – Programmieren mit endlichen Automaten – Kurs: Spielerisch den Marienkäfer „Kara“ als EA programmieren und Aufgaben lösen.
- JFLAP – Java-Programm zum Erstellen von Automaten aller Art (englisch)
- FSM Creator – Programm zum Erstellen von endlichen Automaten (englisch)
- Sinelabore – Erzeugt C/C++/Java Code aus UML Zustandsdiagrammen. Der Fokus liegt auf Embedded Systems. (englisch)
- Automaton – Java-Quellcode-Beispiel für einen endlichen Automaten (englisch, deutsche Kommentare)
- YAKINDU Statechart Tools – Ein Open-Source-Werkzeug zur Spezifikation und Entwicklung von reaktiven, ereignisgesteuerten Systemen mit Hilfe von Zustandsautomaten
- C++ Fsm Framework, ein event getriebenes Zustandsmaschinen Framework für C++ mit PERL script zur Generierung von PLANTUML Dateien zur FSM Dokumentation.
Einzelnachweise
- Pong P. Chu: RTL Hardware Design using VHDL. Wiley Interscience, 2006, ISBN 0-471-72092-5, Kapitel 10, insbesondere 10.4: Moore machine versus Mealy machine.