Geneva (Software)

Geneva
Basisdaten
Maintainer	Rüdiger Berlich, Ariel Garcia
Entwickler	Gemfony scientific UG (haftungsbeschränkt) und weitere Kontributoren
Aktuelle Version	Geneva 1.10.0 ; (20. März 2020)
Betriebssystem	Linux
Programmiersprache	C++
Kategorie	Cloud Computing, Optimierung
Lizenz	Apache License v2.0
	Repository

Geneva (Akronym für Grid-enabled evolutionary algorithms) ist eine in C++ implementierte Programmbibliothek, die miteinander kombinierbare Algorithmen zur näherungsweisen, computergestützten Lösung von Optimierungsproblemen bereitstellt. Jenseits der namensgebenden evolutionären Algorithmen werden weitere Optimierungsalgorithmen unterstützt. Ein für Geneva aufbereitetes Optimierungsproblem umfasst die Definition der $n$ Eingabeparameter einschließlich ihrer Typen sowie eine Abbildungsvorschrift $\mathbb {P} ^{n}\rightarrow \mathbb {R} ^{m}$ , mit der diesen Parametern ein oder mehrere numerische Qualitätsmaßstäbe eindeutig zugeordnet werden. Parametersätze können dabei neben Gleitkommazahl- auch Boolean- und Integer-Werte umfassen, wobei Parametertypen in der Problembeschreibung auch gemischt werden dürfen. Optimierung bedeutet dann die Suche nach Maxima oder Minima einer als Programmcode oder externes Programm vorgegebenen Bewertungsfunktion (Einkriterienoptimierung, $m=1$ ) als Funktion der Eingabeparameter, oder die Suche nach einer Gruppe an zufriedenstellenden Lösungen im Falle der Mehrkriterienoptimierung ( $m>1$ ). Die Geneva-Bibliothek ist unter der Apache-Lizenz v2.0 als Open-Source-Software verfügbar.[1]

Einsatzfelder

Geneva ist besonders für Optimierungsprobleme ausgelegt, die von einer Ausführung in verteilten und parallelen Rechnerumgebungen profitieren. Herausforderungen für den Rechenaufwand sind einerseits eine besonders „verrauschte“ Qualitätsoberfläche (Häufigkeit lokaler Maxima und lokaler Minima) und andererseits der Rechenaufwand, um einzelne Kandidatenlösungen zu bewerten. Eine Kandidatenlösung ist ein vom Optimierungsalgorithmus an die Bewertungsfunktion übergebener Parametersatz. Inhaltliche Einschränkungen bzgl. der von der Bewertungsfunktion modellierten Problemstellung existieren nicht, jedoch muss sie sich auf die von Geneva unterstützten Datentypen beschränken und die eingangs geforderte, eindeutige Abbildung implementieren. Ein im Design von Geneva vorgesehenes Einsatzszenario ist die Bewertung von Kandidatenlösungen durch (auch rechenintensive) Simulationen. In C++ implementierte einfache mathematische Funktionen sind jedoch genauso möglich und werden für das Benchmarking von Geneva verwendet. Einschränkungen hinsichtlich der Implementierung der Bewertungsfunktion können sich jedoch aus der parallelen Ausführung im Geneva-Kontext ergeben.

Funktionalität

Implementierte Algorithmen

Abbildung 1: Parameterscan und Optimierung der „Noisy Parabola“ mit Geneva in zwei Dimensionen

Geneva unterstützt neben Evolutionären Algorithmen (ohne ausschließliche Festlegung auf Floating Point oder Boolean-Parameter) verschiedene andere metaheuristische Optimierungsverfahren.[2][3] Dies sind aktuell

Schwarmalgorithmen
Simulated Annealing (erweitert um die Möglichkeit mehrerer gleichzeitiger Bewertungen)
Einfache Gradientenabstiege (nicht Conjugate Gradient). Hierbei wird in jedem Schritt der Gradient auf der Basis des Differenzenquotienten ermittelt und so näherungsweise die Richtung des steilsten Abfalls der Qualitätsoberfläche bestimmt

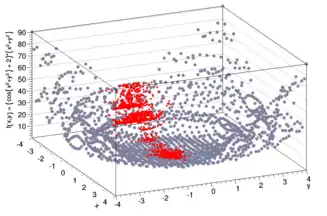
Zusätzlich werden Parameter Scans unterstützt, entweder auf einem regelmäßigen Gitter oder mit Hilfe von über den gesamten Parameterraum gleichverteilten, zufälligen Kandidatenlösungen. Ein Scan der „Noisy Parabola“ $f\left(x_{1},x_{2},\ldots ,x_{n}\right)=\left(cos\left(\sum _{i=1}^{n}x_{i}^{2}\right)+2\right)*\sum _{i=1}^{n}x_{i}^{2}$ (einer in Geneva für Testzwecke verwendeten Funktion mit einer sehr hohen Zahl lokaler Optima) auf einem Gitter ist beispielhaft auf der rechten Seite zu sehen. Dem Scan in Rot überlagert ist eine Optimierung mit Hilfe einer Evolutionsstrategie unter Verwendung von Geneva. Nur einen Teil des Parameterraums unterzieht der evolutionäre Algorithmus der Bewertungsfunktion. Da die Menge zu scannender Raumpunkte exponentiell mit der Zahl der Parameter steigt, stellt die parametrische Optimierung für viele hochdimensionale Problemstellungen den einzig gangbaren Weg zur Lösung dar. Die Geneva-Bibliothek kann hierbei auch mit Problemen mit sehr hohen Zahlen an Parametern[4] umgehen (vgl. hierzu auch Film 1).

Kopplung von Algorithmen

Optimierungsalgorithmen können miteinander gekoppelt werden[2], wobei die besten Lösungen des Vorgängeralgorithmus zum Startwert des folgenden Algorithmus werden. Ein Nutzungsbeispiel ist die Suche nach geeigneten Startpunkten der Optimierung mit Hilfe eines groben Parameterscans, gefolgt von einer Evolutionsstrategie. Der Austausch der besten Kandidatenlösungen zwischen verschiedenen Algorithmen erlaubt grundsätzlich auch die Unterteilung des Optimierungslaufs in Grob- und Fein-Optimierung mit unterschiedlichen Algorithmen.

Behandlung von Randbedingungen

Randbedingungen können den gültigen Teil des Parameterraums stark einschränken. Optimierungsalgorithmen müssen solche Bereiche so weit wie möglich vermeiden, einerseits um schneller ein gültiges Optimum zu erreichen und andererseits, um potentiell fehlerhafte Rückgabewerte der Bewertungsfunktion für ungültige Parameterwerte zu umgehen. Die Geneva Bibliothek unterstützt einerseits die Beschränkung des Wertebereichs einzelner Parameter. Ferner besteht die Möglichkeit, Abhängigkeiten der Randbedingungen einzelner Parameter von den Werten anderer Variablen durch eine Rückführung auf eine gemeinsame Qualitätsoberfläche für ungültige und gültige Lösungen zu behandeln. Ein Beispiel für eine solche Problemstellung wären zwei Parameter x und y, deren Summe einen gegebenen, konstanten Bereich nicht überschreiten darf. Zwar kann in diesem Beispiel grundsätzlich jede Variable variiert werden. Gültige Parameterwerte hängen aber vom aktuellen Wert der jeweils anderen Variable ab.

Das hierbei von Geneva eingesetzte Verfahren[2] bewertet zunächst die Gültigkeit eines Parametersatzes. Gültige Lösungen werden mit Hilfe einer Sigmoid-Funktion transformiert, so dass die Bewertung gültiger Parametersätze eine obere und untere Grenze nicht über- respektive unterschreiten kann. Kann der Nutzer nun für jede verletzte Randbedingung numerisch angeben, wie schwerwiegend deren Verletzung ist, so berechnet Geneva eine Ersatzbewertung (Invalidity), die an die Stelle des Aufrufs der Bewertungsfunktion tritt. Dies geschieht z. B., in dem das Produkt aller Invalidities mit der oberen (bei Minimierung) oder unteren (bei Maximierung) Grenze der Sigmoidfunktion multipliziert wird. Die so entstehende Ersatz-Qualitätsoberfläche fällt in Richtung gültiger Wertebereiche ab. Die durch den Optimierungsalgorithmus gefundenen Lösungen werden so in die Richtung gültiger Werte „gezogen“.

Monitoring

Aktuelle Parameter der Optimierungsalgorithmen sowie der Kandidatenlösungen können während der laufenden Optimierung extrahiert und in Form eines Eingabescripts für das Datenanalysepaket ROOT ausgegeben werden.[2] ROOT sorgt dann für die Konvertierung in gewünschte Bildformate, etwa PNG oder PDF. Ferner ist mit diesem Werkzeug eine Nachbearbeitung (z. B. durch Anmerkungen) außerhalb von Geneva möglich. Daten können entweder mit Algorithmen-spezifischen, vordefinierten Optimierungsmonitoren gesammelt werden, oder mit Hilfe von leichtgewichtigeren, meist Benutzer-definierten Pluggable Optimization Monitors. Abbildung 1 wurde auf diese Weise erzeugt, wobei eine Nachbearbeitung stattgefunden hat.

Parallelisierung und Größe der unterstützten Problemstellungen

Metaheuristische Optimierungsalgorithmen verlaufen in Zyklen, wobei aufeinanderfolgende Iterationen auf den Ergebnissen der Vorgängeriteration aufbauen. Meist erfolgen pro Iteration mehrere Bewertungen, und viele Optimierungsalgorithmen benötigen bei einer Erhöhung der Zahl an Kandidatenlösungen bei gleicher Problemgröße weniger Iterationen bis zu einer zufriedenstellenden Lösung. Die Optimierung von Problemstellungen mit komplexen Qualitätsoberflächen profitiert umgekehrt von zusätzlichen Optimierungszyklen und – insofern vom gewählten Optimierungsalgorithmus unterstützt – pro Iteration der Bewertung einer möglichst großen Anzahl an Kandidatenlösungen.

Die sinnvolle Menge an Iterationen und an Kandidatenlösungen pro Iteration wird insbesondere durch die verfügbare Rechenzeit beschränkt. Durch eine Parallelisierung auf der Ebene der Bewertung von Kandidatenlösungen kann eine Beschleunigung der Optimierungsrechnung erreicht werden. Hierbei ist hilfreich, dass die Einzelbewertungen unterschiedlicher Kandidatenlösungen im Regelfall unabhängig voneinander sind. Für große Populationen an Kandidatenlösungen nähert sich die parametrische Optimierung hinsichtlich der Parallelisiertbarkeit insofern "trivial parallelen" Problemstellungen an.

Der für die Optimierung benötigte Bewertungsschritt kann in Geneva parallel in mehreren Threads oder verteilt in Clustern, Grid oder Cloud erfolgen[5]. Hierbei wird außer der lokalen Berechenbarkeit für gegebene Parametersätze keine inhaltliche Voraussetzung über die verwendeten Bewertungsfunktionen gemacht. Jedoch entstehen durch die gewählte Art der Parallelisierung Anforderungen an die Implementation der Bewertungsfunktion. Bei der Ausführung im Netzwerk ist zudem zu beachten, dass auf Grund der durch das Amdahl'sche Gesetz beschriebenen Einschränkungen sehr kurze Bewertungsfunktionen zu einer schlechten Skalierbarkeit führen.

Metaoptimierung

Es existiert die Möglichkeit, Konfigurationsparameter von Optimierungsalgorithmen (aktuell in Geneva implementiert nur für Evolutionären Algorithmen) direkt zu optimieren, nach Nutzerwahl entweder zwecks Minimierung der Zahl der Aufrufe der Bewertungsfunktion bis zum Erreichen einer vorgegebenen Qualität, oder zur effizienteren Suche nach möglichst guten Optima. Das Verfahren ist durch die Notwendigkeit vieler Optimierungsläufe sehr rechenintensiv und eignet sich nicht für rechenaufwändige Bewertungsfunktionen[2]. Es kann jedoch dazu genutzt werden, anhand schnell zu berechnender mathematischer Funktionen geeignete Konfigurationsparameter auch für sehr verrauschte Qualitätsoberflächen zu bestimmen. Ferner werden durch die Möglichkeit, Optimierungsalgorithmen in Individuen zu kapseln, Multipopulationen unterstützt – sie erlauben es, Optimierungsalgorithmen zum Gegenstand der Optimierung zu machen.

Architektur und Design

Geneva ist ein im C++14-Standard implementiertes Toolkit. Unterstützt werden in der Produktionsversion aktuell nur die gcc- und Clang-Compiler. Geneva verwendet an vielen Stellen Komponenten der Boost-Bibliothekssammlung. Andere externe Bibliotheken werden nur für konkrete Einsatzzwecke verwendet, so etwa passende OpenCL-Implementierungen für ein optionals GPGPU-Backend. Neben der eigentlichen, in der namensgebenden libgeneva-Bibliothek implementierten Optimierungsfunktionalität existieren zwei weitere zentrale Komponenten in Geneva:

Brokering und Netzwerkkommunikation

Alle für die Netzwerkkommunikation und allgemeiner die Verteilung von Rechenaufträgen benötigte Funktionalität ist in der libcourtier implementiert.

Die aktuell auf der Boost ASIO-Bibliothek sowie der Boost Beast-Bibliothek basierende Netzwerkkommunikation implementiert eine einfache Client-Server-Architektur. Sie setzt auf Seiten der Clients lediglich die Erreichbarkeit des Servers voraus. Netzwerkverbindungen werden im Fall von ASIO für jeden Transfer von Parametersätzen oder Bewertungsergebnissen neu geöffnet und nach dem erfolgreichen Transfer der Daten wieder geschlossen. Durch dieses Design muss auf Bibliotheksseite keine Information über die Dauer der Bewertungsfunktion existieren – diese können ggf. auch über viele Stunden aktiv sein. Die Ausführung im Netzwerk stellt je nach Bewertungsfunktion auf Grund einer hohen Frequenz an Client-Server Verbindungen jedoch ähnliche Anforderungen an den Server wie ein Webserver, erfordert also ggf. eine auf Geneva angepasste Konfiguration. Die auf Boost Beast basierende Implementierung verwendet im Vergleich Websockets, so dass Verbindungen über längere Zeit aufrechterhalten werden. Die für die Netzwerkkommunikation notwendige Serialisierung von Objekten ist über die Boost.Serialization Bibliothek implementiert.

Rechenaufträge können durch mehrere Erzeuger an einen Broker übergeben werden, der über Plugins für die Verteilung an Interessenten sowie die Rückübergabe fertiger Rechenaufträge an die Erzeuger sorgt. Neben der Netzwerkkommunikation sind andere Konsumenten möglich. So wurden die Einzelschritte hinter Film 1 etwa mit einem GPGPU-Backend auf Basis von OpenCL erzeugt.

Erzeugung von Zufallszahlen

Viele stochastische Optimierungsverfahren, wie etwa Evolutionäre Algorithmen, benötigen für eine erfolgreiche Optimierung große Mengen an Zufallszahlen – im Fall Evolutionärer Algorithmen meist mit einer Normalverteilung. Da die Optimierung jedoch in Zyklen verläuft, unterliegt die über die Zeit benötigte Rechenleistung periodischen Schwankungen. Entsprechend gibt es Zeiten niedriger Auslastung, die für die Erzeugung von Zufallszahlen verwendet werden können. Die Geneva Bibliothek nutzt dies im Rahmen einer „Zufallszahlenfabrik“ aus, die im Hintergrund in mehreren Threads Puffer mit im Intervall $[0,1[$ gleichverteilten Zufallszahlen füllt (bis zu einer vorgegebenen Grenze). „Proxy-Objekte“ in den Konsumenten können einer Queue der Zufallszahlenfabrik Pakete von Zufallszahlen entnehmen. Diese werden den Konsumenten bei Bedarf einzeln transparent zur Verfügung gestellt – die Proxy-Objekte sehen für diese wie Zufallszahlengeneratoren aus. Hierbei kann bei Bedarf auch die Umrechnung in vom Konsument benötigte Zufallsverteilungen erfolgen. Durch das kontinuierliche Füllen von Puffern mit Zufallszahlen können insbesondere Zeiten niedriger Aktivität besser genutzt werden. Ferner entfallen Probleme mit dem Setzen der Seeds der Generatoren, die dann auftreten würden, wenn jeder der (möglicherweise tausenden von) Konsumenten einen eigenen Generator verwenden würde. Diese Funktionalität ist in der libhap implementiert.

Beispiele

Abbildung 2: Ein Dalitz-Plot aus Monte-Carlo-generierten

J/\psi \rightarrow \gamma \pi \pi

-Zerfällen, unter Verwendung eines ComPWA[4]-Modells. Optimierte Parameter für verschiedene Resonanzen wurden mit Geneva bestimmt.

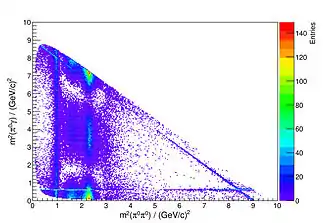
Film 1 zeigt eine mit der Geneva-Bibliothek durchgeführte Optimierung, bei der 150 zufällige, semi-transparente Dreiecke hinsichtlich ihrer Koordinaten, Farbwerte und Durchsichtigkeit so arrangiert werden mussten, dass sie dem Wikipedia-„W“ möglichst ähnlich sahen. Gezeigt sind jeweils nur die besten Lösungen jeder Iteration. Insgesamt bedeutet dies eine Anpassung von 1500 Parametern im Wertebereich [0:1]. Das Bewertungskriterium umfasste dabei die quadratische Summe der numerischen Abweichungen der Farbkanäle aller Pixel zwischen einem aus den für einen gegebenen Parametersatz aus den 150 Dreiecken zusammengesetzten Kandidatenbild und dem Zielbild. Da die Bewertung unterschiedlicher Zielbilder voneinander unabhängig ist, profitiert die Optimierung solcher Problemstellungen stark von der gleichzeitigen Nutzung vieler Prozessoren etwa in einem Mehrkernprozessor. Das Beispiel ist auch insofern interessant, als man bei metaheuristischen Optimierungsverfahren im Regelfall bei vielen Parametern keine Aussage darüber machen kann, wie nahe man am globalen Optimum ist. Im vorliegenden Fall reicht hierfür jedoch trotz der sehr hohen Zahl an Parametern die visuelle Begutachtung. Das Beispiel orientiert sich an einer Idee von Roger Alsing[6] (dort mit der Mona Lisa als Zielbild). Geneva kommt aktuell u. a. in der Teilchenphysik[4][7] (vgl. auch Abbildung 2) sowie in der Automobilindustrie zur Optimierung der Akustik von Abgasanlagen[8] zum Einsatz.

Historie

Vorläufer von Geneva wurden 1994 im Rahmen einer Diplomarbeit am Institut für Experimentalphysik I der Ruhr-Universität Bochum[9] entwickelt und dort für das Training von Feedforward Neuronalen Netzwerken zur Erkennung hadronischer Splitoffs am Crystal-Barrel-Experiment des CERN / Genf eingesetzt. Der Code wurde von 2001 bis 2004 im Rahmen einer Doktorarbeit am selben Institut im Hinblick auf die verteilte Optimierung von Analysen der Elementarteilchenphysik weiterentwickelt[10][11][12]. Im Rahmen einer Ausgründungsförderung am Steinbuch Centre for Computing des Karlsruhe Institute of Technology wurde Geneva komplett überarbeitet und an die KIT-Ausgründung Gemfony scientific UG (haftungsbeschränkt) übergeben[13]. Geneva wurde in diesem Zusammenhang als Open Source freigegeben. Die Geneva-Bibliothek umfasst in der Version 1.10 rund 130.000 Zeilen Code und befindet sich in aktiver Entwicklung.[14] Geneva wurde in der im März 2020 veröffentlichten Version 1.10 unter die Apache-Lizenz in der Version 2.0 gestellt. Bis zu diesem Zeitpunkt stand sie unter der GNU Affero General Public License in der Version 3.0.

Einzelnachweise

Repository der Geneva Bibliothek
Manual der Geneva Bibliothek, Version 1.6; R.Berlich, S.Gabriel, A.Garcia: Parametric Optimization with the Geneva Library Collection; engl.
HadoOptimizer – Lösung komplexer Optimierungsprobleme von Christian Kumpe et al. in SCC News (Publikation des Steinbuch Centre for Computing am Karlsruhe Institute of Technology), Ausgabe 2011/3, S. 24 ff.
ComPWA: A common amplitude analysis framework for PANDA M Michel et al. 2014 J. Phys.: Conf. Ser. 513 022025
Distributed Parametric Optimization with the Geneva Library, Rüdiger Berlich et al., in Data Driven e-Science; Conference proceedings of ISGC 2010; Springer; Simon C. Lin and Eric Yen (editors); ISBN 978-1-4419-8013-7; S. 303 ff.
Modellierung der Mona Lisa mit Dreiecken durch Roger Alsing
Model independent determination of the CKM phase $\gamma$ using input from $D^{0}-{\bar {D}}^{0}$ -mixing, Sam Harnew und Jonas Rademacker, Journal of High Energy Physics, March 2015, 2015:169
Parametrische Optimierung der Akustik von Abgasanlagen (Memento des Originals vom 4. März 2016 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2Vorlage:Webachiv/IABot/www.atzlive.de, Dominik Rödel und Rüdiger Berlich, 2. Internationaler Motorenkongress 2015, Februar 2015, Baden-Baden
R.Berlich: Visualisierung hadronischer Splitoffs und ihre Erkennung mit neuronalen Netzen, Diplom-Arbeit, Institut für Experimentalphysik I der Ruhr-Universität Bochum, 1995
R.Berlich: Application of Evolutionary Strategies to Automated Parametric Optimization Studies in Physics Research, Doktorarbeit, Institut für Experimentalphysik I der Ruhr-Universität Bochum, 2004
R.Berlich, M.Kunze: Parametric optimization with evolutionary strategies in particle physics, Nuclear Instruments and Methods in Physics Research A 534 (2004) 147–151
Das Beste zum Schluss – Optimierungsalgorithmen auf verteilten Systemen, Rüdiger Berlich, iX, Heise Zeitschriftenverlag, Ausgabe 12/2010, S. 110–115.
"Geneva -- von der Forschung zur wirtschaftlichen Anwendung", Rüdiger Berlich in SCC News (Publikation des Steinbuch Centre for Computing am Karlsruhe Institute of Technology), Ausgabe 2009/2, S. 8 ff.
Analyse des Geneva-Codes durch BLACKDUCK / Open Hub

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[LAUNCHPADGENEVA-1] Repository der Geneva Bibliothek

[GENEVAMANUAL-2] Manual der Geneva Bibliothek, Version 1.6; R.Berlich, S.Gabriel, A.Garcia: Parametric Optimization with the Geneva Library Collection; engl.

[HADOOPTIMIZERSCCNEWS-3] HadoOptimizer – Lösung komplexer Optimierungsprobleme von Christian Kumpe et al. in SCC News (Publikation des Steinbuch Centre for Computing am Karlsruhe Institute of Technology), Ausgabe 2011/3, S. 24 ff.

[MMICHELPWA-4] ComPWA: A common amplitude analysis framework for PANDA M Michel et al. 2014 J. Phys.: Conf. Ser. 513 022025

[ISGC09GENEVA-5] Distributed Parametric Optimization with the Geneva Library, Rüdiger Berlich et al., in Data Driven e-Science; Conference proceedings of ISGC 2010; Springer; Simon C. Lin and Eric Yen (editors); ISBN 978-1-4419-8013-7; S. 303 ff.

[MLROGERALSING-6] Modellierung der Mona Lisa mit Dreiecken durch Roger Alsing

[HARNEWMIX-7] Model independent determination of the CKM phase $\gamma$ using input from $D^{0}-{\bar {D}}^{0}$ -mixing, Sam Harnew und Jonas Rademacker, Journal of High Energy Physics, March 2015, 2015:169

[ATZBB-8] Parametrische Optimierung der Akustik von Abgasanlagen (Memento des Originals vom 4. März 2016 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2Vorlage:Webachiv/IABot/www.atzlive.de, Dominik Rödel und Rüdiger Berlich, 2. Internationaler Motorenkongress 2015, Februar 2015, Baden-Baden

[BERLICHDIPLOM-9] R.Berlich: Visualisierung hadronischer Splitoffs und ihre Erkennung mit neuronalen Netzen, Diplom-Arbeit, Institut für Experimentalphysik I der Ruhr-Universität Bochum, 1995

[BERLICHPHD-10] R.Berlich: Application of Evolutionary Strategies to Automated Parametric Optimization Studies in Physics Research, Doktorarbeit, Institut für Experimentalphysik I der Ruhr-Universität Bochum, 2004

[NIM-11] R.Berlich, M.Kunze: Parametric optimization with evolutionary strategies in particle physics, Nuclear Instruments and Methods in Physics Research A 534 (2004) 147–151

[IXGENEVA-12] Das Beste zum Schluss – Optimierungsalgorithmen auf verteilten Systemen, Rüdiger Berlich, iX, Heise Zeitschriftenverlag, Ausgabe 12/2010, S. 110–115.

[GENEVASCCNEWS-13] "Geneva -- von der Forschung zur wirtschaftlichen Anwendung", Rüdiger Berlich in SCC News (Publikation des Steinbuch Centre for Computing am Karlsruhe Institute of Technology), Ausgabe 2009/2, S. 8 ff.

[BLACKDUCKGENEVA-14] Analyse des Geneva-Codes durch BLACKDUCK / Open Hub