Mutation (evolutionärer Algorithmus)
Unter Mutation versteht man bei einem evolutionären Algorithmus (EA) die zufällige Änderung eines Genoms. Sie ist die Umsetzung der biologischen Mutation für EA. Eine solche Zuordnung von einem alten Genom (und eventuell Zufallszahlen) zu einem neuen Genom ist eine Funktion und heißt Mutations-Funktion. Jede Mutations-Funktion ist ein genetischer Operator.
Alle in einem EA zur Anwendung kommenden Mutationsoperatoren müssen in ihrer Gesamtheit folgenden Anforderungen genügen:
- Kleine Änderungen müssen wahrscheinlicher sein als große.
- Jeder Punkt im Suchraum muss durch eine oder mehrere Mutationen erreichbar sein.
- Es darf keine Bevorzugung von Teilen oder Richtungen im Suchraum (keine Drift) geben.
Am Anfang eines EA-Laufs ist es günstiger, größere Änderungen zuzulassen, während im fortgeschritteneren Stadium nur noch kleine Änderungen bevorzugt sein sollten, um Individuen, die sich bereits nahe einem Optimum befinden, nicht von diesem Optimum wegzubringen.
Ein evolutionärer Algorithmus mit einer globalen Mutationsrate (Anteil der Gesamtpopulation, die der Mutation unterzogen wird) von 0 wird sehr schlechte Ergebnisse liefern, da einmal durch Kreuzungsfunktionen aus der Population gefallene Allele niemals wieder in die Population zurückkehren können und somit, falls sie ein Teil (Building Blocks bei klassischen genetischen Algorithmen) der global optimalen Lösung waren, zum Auffinden dieser fehlen. Ist die Mutationsrate hingegen zu hoch, werden Individuen nahe beim Optimum wieder von diesem weggedrängt und der Algorithmus kann schlechter konvergieren.
Bei Verwendung von für das Problem nicht gut geeigneten Kreuzungsfunktionen oder Problemrepräsentationen kann es zu ungewollten Mutationen bei der Kreuzung kommen. Dabei entsteht an manchen Stellen des Chromosoms eine Ausprägung des Allels, die sich auf keinen der Elternindividuen zurückführen lassen, noch bevor es zum eigentlichen Mutationsschritt kommt.
Für unterschiedliche Genom-Typen eignen sich unterschiedliche Mutations-Typen unterschiedlich gut:
Mutation von binären Zahlen (Bitstrings)
Die Mutation von Bitstrings der klassischen genetischen Algorithmen erfolgt durch Bit-Flips an zufälligen Stellen.
Beispiel:
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| ↓ | ||||||
| 1 | 0 | 1 | 0 | 1 | 1 | 0 |
Die Wahrscheinlichkeit für eine Mutation eines Bits beträgt , wobei die Länge des Binärvektors ist. Dadurch wird im Schnitt eine Mutationsrate von 1 je Mutation und zur Mutation gewählten Individuum erreicht (siehe oben, globale Mutationsrate).
Bevorzugung der niederwertigeren Bits
Eine Variante der Mutation von binären Zahlen ist folgendes Verfahren:
- Wähle eine Stelle der binären Zahl , wobei die niederwertigen Stellen mit einer exponentiell höheren Wahrscheinlichkeit ausgewählt werden als die höherwertigen.
- Invertiere das Bit an dieser Stelle der binären Zahl um: .
- Die auf diese Weise neu entstandene Zahl ist das mutierte Genom.
Ein Beispiel zur Veranschaulichung – eine Mutation einer 8-Bit-Zahl:
- 11001100 – die Zahl vor der Mutation
- 11000100 – danach (eine Mutation an der 4. Stelle)
Dieses Verfahren funktioniert auch bei Gleitkommazahlen, wenn diese als Zahl ohne Exponenten-Information geschrieben wird (also statt ).
Eine falsche Wahl der Mutationswahrscheinlichkeiten kann dazu führen, dass immer nur niederwertigen Stellen modifiziert werden, sodass die Mutationen letztendlich gar keinen nennenswerten Einfluss auf die Individuen oder den von ihnen abhängige Fitness-Funktions-Wert haben.
Mutation reeller Zahlen
Viele EAs wie zum Beispiel die Evolutionsstrategie[1][2] oder die reell-codierten genetischen Algorithmen[3][4] arbeiten mit reellen Zahlen anstelle von Bitstrings. Dies liegt in den guten Erfahrungen begründet, die mit dieser Codierungsart gemacht wurden[5][6] und in der Theorie der virtuellen Alphabete von David E. Goldberg.
Der Wert eines reellwertigen Gens kann entweder verändert oder neu bestimmt werden. Eine Mutation, die letzteres umsetzt, sollte immer nur in Verbindung mit den Wert ändernden Mutationen eingesetzt werden und dann auch nur mit vergleichsweise geringer Wahrscheinlichkeit, da sie zu großen Änderungen führen kann.
Bei praktischen Anwendungen sind die zu verändernden Entscheidungsvariablen des zu bearbeitenden Optimierungsproblems in der Regel begrenzt. Dem entsprechend sind die Werte der zugehörigen Gene jeweils auf ein Werteintervall eingeschränkt. Mutationen können diese Restriktionen berücksichtigen oder nicht. Im letzten Fall ist dann eine geeignete Nachbehandlung erforderlich.
Mutation ohne Berücksichtigung von Restriktionen
.svg.png.webp)
Eine reelle Zahl kann mittels der Normalverteilung mutiert werden, wobei eine normalverteilte Zufallszahl bei dieser Verteilung bekanntlich mit rund 99,7 % Wahrscheinlichkeit im Intervall liegt. Der mutierte Wert ergibt sich dann folgendermaßen:
Bei Genen mit eingeschränktem Wertebereich bietet es sich an, die Schrittweite der Mutation so zu wählen, dass sie zum Werteintervall des zu verändernden Gens einigermaßen passt, also z. B.:
Natürlich kann auch stattdessen vom kleineren Intervall zwischen dem aktuellen Wert von und den Grenzen ausgegangen werden, solange dies nicht zu klein im Vergleich zum gesamten Wertebereich ist. Es wird aber in jedem Fall mit einer gewissen Wahrscheinlichkeit vorkommen, dass sich der neue Wert des Gens außerhalb des Wertebereichs befindet. In einem solchen Fall liegt eine Letalmutation vor, da die naheliegende Reparatur durch Verwendung der jeweils verletzten Grenze als neuen Wert des Gens zu einer Drift führen würde. Denn der Grenzwert würde dann mit der gesamten Wahrscheinlichkeit der Werte jenseits der Grenze des Wertebereichs ausgewählt werden. Im Bild ist dies z. B. der gesamte Bereich rechts von 1σ, wenn dies beispielhaft der Obergrenze des Wertebereichs des Gens entspräche. Das ergäbe dann immerhin eine Wahrscheinlichkeit von rund 15,8 % nur für diesen einen Wert.
Die Evolutionsstrategie arbeitet mit reellen Zahlen und ebenfalls einer Mutation basierend auf der Normalverteilung. Die Schrittweiten sind dabei Bestandteil des Chromosoms und unterliegen zusammen mit den eigentlichen Entscheidungsvariablen der Evolution.
Mutation mit Berücksichtigung von Restriktionen
Eine mögliche Form der Werteänderung eines Gens unter Berücksichtigung seines Wertebereichs ist die Mutation „relative Parameteränderung“ des evolutionären Algorithmus GLEAM (General Learning Evolutionary Algorithm and Method),[7][8] bei der wie bei der zuvor vorgestellten Mutation kleine Veränderungen wahrscheinlicher sind als große.
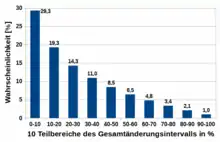
Zuerst wird gleichverteilt entschieden, ob der aktuelle Wert vergrößert oder verkleinert werden soll und dann das zugehörige Gesamtänderungsintervall bestimmt. Ohne Beschränkung der Allgemeinheit wird für die Erklärung von einer Vergrößerung ausgegangen und das Gesamtänderungsintervall lautet dann . Es wird in zehn gleichgroße Teilbereiche mit der Breite eingeteilt, aus denen zehn unterschiedlich große Teiländerungsintervalle gebildet werden:
- -tes Teiländerungsintervall: mit und
Anschließend wird gleichverteilt eines der zehn Teiländerungsintervalle ausgewählt und daraus eine ebenfalls gleichverteilte Zufallszahl als neuer Wert für das Gen gezogen. Die sich daraus ergebenden summierten Wahrscheinlichkeiten der zehn Teiländerungsintervalle ergeben die im Bild dargestellte Verteilung für die zehn Teilbereiche. Dies ist zwar keine Normalverteilung wie zuvor, aber auch diese Verteilung bevorzugt deutlich kleine Änderungen vor größeren.
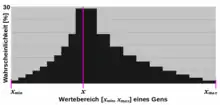
Die Wahrscheinlichkeiten der Teilbereiche eines Gens, für die Änderung ausgewählt zu werden, gibt das nebenstehende Bild für seinen gesamten Wertebereich wieder. Man beachte, dass die Flächen nur jeweils rechts oder links vom aktuellen Wert proportional zur jeweiligen Änderungswahrscheinlichkeit sind, da die Wahrscheinlichkeit für eine Vergrößerung oder Verkleinerung zuerst und unabhängig vom aktuellen Wert des Gens bestimmt wird.
Es sei angemerkt, dass diese Mutation weniger gut für Aufgabenstellungen geeignet ist, bei denen das Optimum auf einer Grenze des zulässigen Wertebereichs liegt. Im Fall großer Annäherung eines Genwertes an seine Grenzen kann aber die Mutation leicht geeignet verändert werden, z. B. indem dann einfach der neue Wert aus dem kleinen Restbereich gleichverteilt ausgewürfelt wird.
Gemeinsame Eigenschaften
Bei beiden Mutationsoperatoren für reellwertige Zahlen ist die Wahrscheinlichkeit für eine Vergrößerung und Verkleinerung unabhängig vom aktuellen Wert und beträgt jeweils 50 %. Außerdem sind kleine Änderungen erheblich wahrscheinlicher als große. Bei gemischt ganzzahligen Problemen wird üblicherweise gerundet.
Mutation von Permutationen
Die Mutation von Permutationen ist spezielle für Genome ausgelegt, die selbst Permutationen einer Menge sind. Dabei werden Teile des Genoms verschoben oder gespiegelt.
Rotation nach rechts
Eine Variante von Mutation von Permutationen ist folgendes Verfahren:
| Verfahren | Beispiel |
| Gegeben ist eine Permutation, | |
| * Wähle eine Teil-Liste aus, also einen Start-Index und einen End-Index in , die beide natürliche Zahlen zwischen 0 und sind. Wähle die Anzahl der Positionen aus, um die die Teil-Liste rotiert werden soll, wobei gilt . Der Start-Index kann dabei auch nach dem End-Index kommen. Dann fängt die Teil-Liste einfach von vorne wieder an (periodische Randbedingung). Dies ist notwendig, damit die Permutationswahrscheinlichkeit im Genom überall gleich ist und nicht in der Mitte größer ist als an den Rändern. | , , |
| * Kopiere nach und rotiere die Teil-Liste um Positionen nach rechts. | |
| * ist dann das mutierte Genom. |
Spiegelung
Eine weitere Variante von Mutation von Permutationen ist folgendes Verfahren:
| Verfahren | Beispiel |
| * Gegeben ist eine Permutation, | |
| * Wähle eine Teil-Liste aus, also einen Start-Index und einen End-Index in , die beide natürliche Zahlen zwischen 0 und sind und gilt. Diese Bedingung bewirkt, dass die Mutation immer ein genotypisch verändertes Chromosom erzeugt. Der Start-Index kann dabei auch nach dem End-Index kommen. Dann fängt die Teil-Liste einfach von vorne wieder an (periodische Randbedingung). Dies ist notwendig, damit die Permutationswahrscheinlichkeit im Genom überall gleich ist und nicht in der Mitte größer ist als an den Rändern. | , |
| * Kopiere nach und spiegele die Teil-Liste. | |
| * ist dann das mutierte Genom. |
Varianten mit Bevorzugung kleiner Änderungen
Die eingangs erhobene Anforderung an Mutationen, wonach kleine Änderungen wahrscheinlicher sein sollen als große, wird durch die beiden Permutationsmutationen nur unzureichend erfüllt, da die Längen der Teillisten und die Anzahl der Verschiebungspositionen gleichverteilt bestimmt werden. Je länger aber die Teilliste und die Verschiebung ausfallen, desto größer ist die Änderung an der Genreihenfolge.
Dem kann durch folgende Modifikationen abgeholfen werden. Der Endindex der Teillisten wird als Distanz zum Startindex bestimmt:
wobei zufällig nach einem der beiden Verfahren für die Mutation reeller Zahlen aus dem Intervall bestimmt wird. Legt man die Mutation ohne Berücksichtigung von Restriktionen zu Grunde, so kann das so gewählt werden, dass es einem Drittel der Intervallbreite entspricht und von der sich ergebenden normalverteilten Zufallszahl wird der Betrag genommen. Bei beiden Verfahrenen ist die resultierende reelle Zahl für auf ganze Zahlen zu runden.
Bei der Rotation wird ähnlich wie die Distanz bestimmt, wobei jedoch der Wert verboten ist.
Bei der Spiegelung ist zu beachten, dass sein muss, also ist für der Wert auszuschließen.
Diese Varianten sind z. B. zur Lösung vom Problem des Handlungsreisenden geeignet, da hier die Änderung der Nachbarschaft minimal gehalten werden sollte und durch die Spiegelung einfach ein Teil-Weg in umgekehrter Reihenfolge gegangen wird.
Einzelnachweise
- Ingo Rechenberg: Evolutionsstrategie; Optimierung technischer Systeme nach Prinzipien der biologischen Evolution. Frommann-Holzboog, Stuttgart-Bad Cannstatt 1973, ISBN 3-7728-0373-3.
- Hans-Paul Schwefel: Numerische Optimierung von Computor-Modellen mittels der Evolutionsstrategie : mit einer vergleichenden Einführung in die Hill-Climbing- und Zufallsstrategie. Birkhäuser, Basel 1977, ISBN 3-7643-0876-1.
- Larry J. Eshelman, J. David Schaffer: Real-Coded Genetic Algorithms and Interval-Schemata. In: Foundations of Genetic Algorithms. Band 2. Elsevier, 1993, ISBN 978-0-08-094832-4, S. 187–202, doi:10.1016/b978-0-08-094832-4.50018-0 (elsevier.com [abgerufen am 15. Januar 2022]).
- Cesary Janikow, Zbigniew Michalewicz: An Experimental Comparison of Binary and Floating Point Representations in Genetic Algorithms. In: Conf. Proc of the Fourth Int. Conf. on Genetic Algorithms (ICGA'91). 1991, S. 31–36 (umsl.edu [PDF]).
- Zbigniew Michalewicz: Genetic Algorithms + Data Structures = Evolution Programs. Third, revised and Extended edition Auflage. Springer, Berlin, Heidelberg 1996, ISBN 978-3-662-03315-9.
- F. Herrera, M. Lozano, J.L. Verdegay: Tackling Real-Coded Genetic Algorithms: Operators and Tools for Behavioural Analysis. In: Artificial Intelligence Review. Band 12, Nr. 4, 1998, S. 265–319, doi:10.1023/A:1006504901164 (springer.com [abgerufen am 15. Januar 2022]).
- Christian Blume, Wilfried Jakob: GLEAM - General Learning Evolutionary Algorithm and Method : ein Evolutionärer Algorithmus und seine Anwendungen. KIT Scientific Publishing, 2009, doi:10.5445/ksp/1000013553 (uni-karlsruhe.de [abgerufen am 22. Januar 2022]).
- Christian Blume, Wilfried Jakob: GLEAM - An Evolutionary Algorithm for Planning and Control Based on Evolution Strategy. In: Conf. Proc. of Genetic and Evolutionary Computation Conference (GECCO 2002). vol. Late Breaking Papers, 2002, S. 31–38 (kit.edu).