Binärer Suchbaum
In der Informatik ist ein binärer Suchbaum eine Kombination der abstrakten Datenstrukturen Suchbaum und Binärbaum. Ein binärer Suchbaum, häufig abgekürzt als BST (von englisch Binary Search Tree), ist ein binärer Baum, bei dem die Knoten „Schlüssel“ tragen, und die Schlüssel des linken Teilbaums eines Knotens nur kleiner (oder gleich) und die des rechten Teilbaums nur größer (oder gleich) als der Schlüssel des Knotens selbst sind.
Was die Begriffe „kleiner gleich“ und „größer gleich“ bedeuten, ist völlig dem Anwender überlassen; sie müssen nur eine Totalordnung (genauer: eine totale Quasiordnung siehe unten) etablieren. Am flexibelsten wird die Ordnungsrelation durch eine vom Anwender zur Verfügung zu stellende 3-Wege-Vergleichsfunktion realisiert. Auch ob es sich um ein einziges Schlüsselfeld oder eine Kombination von Feldern handelt, ist Sache des Anwenders; ferner ob Duplikate (unterschiedliche Elemente, die beim Vergleich aber nicht als „ungleich“ herauskommen) zulässig sein sollen oder nicht. Über Suchfunktionen für diesen Fall siehe unten.
Ein in-order-Durchlauf durch einen binären Suchbaum ist äquivalent zum Wandern durch eine sortierte Liste (bei im Wesentlichen gleichem Laufzeitverhalten). Mit anderen Worten: ein binärer Suchbaum bietet ggf. wesentlich mehr Funktionalität (zum Beispiel Durchlauf in der Gegenrichtung und/oder einen „direkten Zugriff“ mit potentiell logarithmischem Laufzeitverhalten – erzielt durch das Prinzip „Teile und herrsche“, das auf der Fernwirkung des Transitivitätsgesetzes beruht) bei einem gleichen oder nur unwesentlich höheren Speicherbedarf.
Motivation
Suchbäume sind Lösungen des sogenannten „Wörterbuchproblems“. Angenommen ist eine große Anzahl von Schlüsseln, denen jeweils ein Wert beigegeben ist. In einem Wörterbuch deutsch–englisch ist das deutsche Wort der Schlüssel und englische Wörter sind der gesuchte Wert. Ähnlich verhält es sich bei einem Telefonbuch mit Namen und Adresse als Schlüssel und der Telefonnummer als dem gesuchten Wert.
Mathematisch gesehen realisiert ein Wörterbuch eine (endliche) Funktion mit Paaren (Schlüssel, Wert). Bei der Suche wird ein Suchbegriff (Argument der Funktion) mit einem der Schlüssel zur Deckung gebracht. Hat dies Erfolg, wird dem Suchbegriff der beigegebene Wert als Funktionswert zugeordnet.[1]
In beiden Beispielen sind üblicherweise die Schlüssel sortiert. Das ist sehr zweckmäßig, denn es erlaubt, das Buch in der Mitte aufzuschlagen und zu überprüfen, ob der Suchbegriff gefunden ist. Ist er nicht gefunden und liegt er beispielsweise alphabetisch vor dem Buchstaben »K«, weiß man zusätzlich, dass man nicht weiter hinten mit »L«, »M« oder »Z« vergleichen muss. Der zur Untersuchung übrig bleibende Teil ist immer ein zusammenhängendes Segment, welches wie das ganze Buch am Anfang wieder halbiert wird – und so weiter bis zum Fund oder bis festzustellen ist, dass der Suchbegriff nicht vorkommt.
Diese Vorgehensweise hat in der Informatik den Namen „binäres Suchen“. Sie wird auf naheliegende Weise durch das sehr bekannte Suchverfahren „binäre Suche im Array“ nachgebildet. Ihr Verhalten ist informationstheoretisch optimal, nämlich logarithmisch, genauer: Bei Schlüsseln benötigt man maximal (Abrundungsfunktion und Aufrundungsfunktion) Vergleiche.
Anders als beim binären Suchen muss beim „sequentiellen Suchen“ der Suchbegriff potentiell mit allen Schlüsseln verglichen werden. (Dafür braucht allerdings die Eingabe nicht sortiert zu sein.) Der Unterschied zwischen den beiden Verfahren kann erheblich sein: In einem Telefonbuch mit Einträgen, müssen beim sequentiellen Suchen im Mittel Vergleiche durchgeführt werden. Beim binären Suchen gelangt man nach maximal Vergleichen zum selben Ergebnis.
Änderungen, Zugänge und Abgänge bei Wörter- und Telefonbüchern können sporadisch, bei Softwaresystemen müssen sie in der Regel unmittelbar reflektiert werden. Zugänge und Abgänge erfordern in einem Array Datentransporte, deren Aufwand proportional zur Länge des Arrays, also linear in ist. Ein solcher Aufwand macht die Effizienz des binären Suchens völlig zunichte.
Die Vorgehensweise beim binären Suchen lässt sich auch mit einem Binärbaum nachbilden. Der erste Schlüssel, mit dem der Suchbegriff zu vergleichen ist, wird in die Wurzel des Binärbaums platziert. Der beim Vergleichsergebnis »kleiner« aufzusuchende nächste Schlüssel wird in den linken Kindknoten platziert und entsprechend der Schlüssel für »größer« in den rechten Kindknoten. So fährt man fort, bis alle Schlüssel im Binärbaum untergebracht sind. (Dadurch wird der Binärbaum zu einem binären Suchbaum.)
Durch das Herauslösen der einzelnen Elemente aus dem Array wird große Flexibilität gewonnen: Der Aufwand beim Einfügen für das Zuweisen von Speicherplatz und Beschicken der Felder mit Werten sowie beim Löschen für die Rückgabe des Speicherplatzes ist unabhängig von der Anzahl der Elemente. Verloren geht beim Binärbaum allerdings ein Maß für die Balance, das beim Array durch das Bilden des Mittelwerts zwischen zwei Indizes gegeben ist. Darüber hinaus kann ein Binärbaum, der einmal hervorragend balanciert war, durch Einfügungen und Löschungen seine Balance verlieren und im Extremfall, wenn nämlich jeder Knoten nur noch einen Kindknoten hat (statt zwei), zu einer linearen Liste degenerieren – mit dem Ergebnis, dass eine Suche einer sequentiellen Suche gleichkommt.
Die Informatiker haben verschiedene Balance-Kriterien für Binärbäume entwickelt. Bei den meisten sind die Aufwände für das Suchen, Einfügen und Löschen logarithmisch, wenn auch mit unterschiedlichen konstanten Faktoren. Einige Lösungsprinzipien zur Problematik der Entartung bei dynamischen Binärbäumen finden sich im

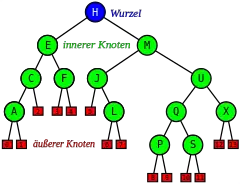
Wurzel , 13 innere Knoten (grün und blau) und 14 äußere Knoten (rot); die inneren mit den Schlüsseln der Abb. 1A
Terminologie
Die Begriffe Knoten und Kante, letztere definitionsgemäß als gerichtete Kante (oder auch Bogen und Pfeil), werden von den allgemeinen Graphen übernommen. Wenn die Gerichtetheit aus dem Kontext klar genug hervorgeht, genügt Kante.
Bei gerichteten Graphen kann man einem Knoten sowohl Ausgangsgrad wie Eingangsgrad zuordnen. Üblicherweise werden Binärbäume als Out-Trees aufgefasst. In einem solchen gewurzelten Baum gibt es genau einen Knoten, der den Eingangsgrad 0 hat. Er wird als die Wurzel bezeichnet. Alle anderen Knoten haben den Eingangsgrad 1. Der Ausgangsgrad ist die Anzahl der Kindknoten und ist beim Binärbaum auf maximal 2 beschränkt. Damit ist seine Ordnung als Out-Tree ≤ 2.
Knoten mit Ausgangsgrad ≥ 1 bezeichnet man als interne (innere) Knoten, solche mit Ausgangsgrad 0 als Blätter oder externe (äußere) Knoten. Bei Binärbäumen – und nur dort – findet sich gelegentlich die Bezeichnung Halbblatt für einen Knoten mit Ausgangsgrad 1 (englisch manchmal: non-branching node). Dann ist ein Blatt ein doppeltes Halbblatt.
Unterschiedliche Sprechweisen
Den Knoten des Binärbaums in der Abb. 1A sind Schlüssel in Gestalt von Großbuchstaben zugeordnet. Da bei der in-order-Traversierung deren (alphabetische) Sortierordnung befolgt wird, ist der Baum ein binärer Suchbaum.
In der Abb. 1B ist die identische Schlüsselmenge in einem anderen binären Suchbaum dargestellt, einem Suchbaum, der explizite „NIL-Knoten“ enthält. Hier tragen nur die internen Knoten Schlüssel, wogegen die externen, die NIL-Knoten (auch externe Blätter genannt), als Platzhalter für die Intervalle zwischen den Schlüsseln (so beispielsweise in der Abb. 3), also als Einfügepunkte des binären Suchbaums fungieren. (Der Knoten mit dem Schlüssel ist hier ein internes Blatt.) Knoten mit Ausgangsgrad 1 gibt es nicht. Der schlüssellose Suchbaum besteht aus genau einem Knoten, der extern und Wurzel zugleich ist. Da bei dieser Sichtweise die Höhe des (total) leeren Baums (der kein Suchbaum ist) zu −1 definiert ist, somit dem schlüssellosen Baum die Höhe 0 zukommt, stimmen die Höhenbegriffe überein, wenn in der Sichtweise der Abb. 1A dem leeren und zugleich schlüssellosen Baum die Höhe 0 und einem Baum, der nur aus einem Knoten besteht, die Höhe 1 zugeteilt wird.[2]
Knotenorientierte und blattorientierte Speicherung
Wenn – wie oben und in der Abb. 1A – die Inhalte der Menge in den Knoten abgespeichert werden und die externen Knoten leer sind, nennt man die Art der Speicherung knotenorientiert. Um auszudrücken, dass sie nicht zur Menge gehören, bezeichnet man in diesem Fall die externen Knoten zur besseren Unterscheidung als externe Blätter. Ein externes Blatt stellt einen Einfügepunkt dar.
Bei der blattorientierten Speicherung sind die Inhalte der Menge in den Blättern abgespeichert, und die Knoten stellen nur Hinweisschilder für die Navigation dar, die möglicherweise mit den Schlüsseln der Menge wenig zu tun haben.[3]
Begriffsklärung
Zur Beachtung:
- Der Begriff „Nachbar“ (und „Nachbarschaft“ etc.) wird in diesem Artikel (und bei den Suchbäumen generell) anders als sonst in der Graphentheorie verwendet, nämlich ausschließlich im Sinn der eingeprägten Ordnungsrelation: „rechter“ Nachbar meint den nächsten Knoten in aufsteigender Richtung, „linker“ in absteigender.
- Muss in diesem Artikel auf die Hierarchiestruktur des Baumes eingegangen werden, so werden Begriffe wie „Elter“ oder „Vorfahr“ bzw. „Kind“ oder „Nachfahr“ verwendet.
- Die hierarchische Anordnung der Knoten in der Baumstruktur des binären Suchbaums wird als sekundär und mehr oder minder zufällig angesehen – ganz im Vordergrund steht die korrekte Darstellung der Reihenfolge.
- Ähnlich sekundär ist die Frage, welcher Knoten gerade die Rolle der Wurzel spielt, insbesondere wenn es sich um einen selbst-balancierenden Baum handelt. Insofern eignet die Adresse der Wurzel sich nicht zur Identifizierung des Baumes.
- Dagegen kann die feste Adresse eines Zeigers zur Wurzel als Identifikation des Baumes genommen werden, dessen Zeigerwert dann aber auch von den Operationen des Baums zu pflegen ist.
Ordnungsrelation
Damit binäres Suchen, Sortieren etc. funktionieren kann, muss die Ordnungsrelation eine totale Quasiordnung, im Englischen „total preorder“, sein. Die Bezeichnungen für die induzierte Duplikatrelation und die induzierte strenge Halbordnung seien wie dort.
Die Trichotomie einer entsprechenden 3-Wege-Vergleichsfunktion [4] – von ihrem Ergebnis ist nur das Vorzeichen relevant – ergibt sich folgendermaßen:
| , | falls | ( kleiner als ), | ||
| , | falls | ( Duplikat von ), | ||
| , | falls | ( größer als ). |
Nach Vertauschung von und und einer Umordnung erkennt man, dass
- .
Die induzierte Ordnungsrelation ist eine strenge schwache Ordnung, im Englischen strict weak ordering. Sie induziert auf den Äquivalenzklassen dieser Relation, genauer: den Äquivalenzklassen der Duplikatrelation, eine strenge Totalordnung.
Offensichtlich lässt sich jede solche Ordnung spiegeln, d. h. mit vertauschen, das Ergebnis ist wieder eine strenge schwache Ordnung. Nachbarschaftsbeziehungen bleiben bestehen, es wird nur „größer“ mit „kleiner“ bzw. „rechts“ mit „links“ vertauscht.
Anmerkungen:
- Zum reinen Aufsuchen genügt im Grunde eine 2-Wege-Vergleichsfunktion, die angibt, ob zwei „Schlüssel“ gleich sind oder nicht. Mit einer solchen Vergleichsfunktion sind aber effiziente, zum Beispiel im Mittel logarithmische, Suchzeiten nicht erreichbar.
- Für das Funktionieren des Sortierens und binären Suchens ist es unerheblich, ob das Aufspalten des Ungleich-Weges einer 2-Wege-Vergleichsfunktion in einen Kleiner- und einen Größer-Weg ein Artefakt ist, wie zum Beispiel die Anordnung der Buchstaben in einem Alphabet, oder ob eine Näher-/Ferner- oder logische Beziehung (mit) im Spiel ist.
- Spiegelt die Ordnungsrelation auch Nachbarschaft wider, kann diese für ein effizientes „unscharfes Suchen“ ausgenutzt werden.
- Die knotenorientierte Speicherung passt exakt zur Suche mit der 3-Wege-Vergleichsfunktion.
- Wie im folgenden Abschnitt „Suchen“ näher ausgeführt, ist die Behandlung von Duplikaten unabhängig davon, ob die Ordnungsrelation Duplikate zulässt (totale Quasiordnung bzw. strenge schwache Ordnung) oder nicht (Totalordnung bzw. strenge Totalordnung). Einerseits kann es unerwünscht sein, auch wenn sie Duplikate zulässt, diese im Baum zu haben. Andererseits kann es durchaus angebracht sein, auch bei einer Totalordnung Duplikate in den Baum aufzunehmen, zum Beispiel aus dem Eingabestrom. Es kommt in der praktischen Anwendung also nur darauf an, ob es im Baum Duplikate geben soll oder nicht. Konsequenterweise wird hier von vornherein von totalen Quasiordnungen ausgegangen.
Suchen
Die Suche nach einem Eintrag verläuft derart, dass der Suchschlüssel zunächst mit dem Schlüssel der Wurzel verglichen wird. Sind beide gleich, so ist der Eintrag (oder ein Duplikat) gefunden.
Andernfalls (bei „ungleich“) wird überprüft, ob der Suchschlüssel kleiner (größer) ist als der Schlüssel im Knoten: dann wird die Suche rekursiv im linken (rechten) Teilbaum der Wurzel fortgeführt; gibt es keinen linken (rechten) Teilbaum, so existiert der gesuchte Eintrag im binären Suchbaum nicht.
Der auf diese Weise erhaltene finale „ungleich“-Knoten stellt zusammen mit der letzten Vergleichsrichtung den sog. Einfügepunkt für das gesuchte Element dar. (In der Sichtweise der Abb. 1B genügt der externe Knoten, der die Richtung mitenthält.) Wird es hier eingefügt, dann stimmt die in-order- mit der Sortier-Reihenfolge überein. Der finale „ungleich“-Knoten hat einen Schlüssel, der entweder der kleinste unter den größeren ist oder der größte unter den kleineren. Dasselbe gilt spiegelbildlich für seinen Nachbarknoten in der letzten Vergleichsrichtung, sofern es einen solchen gibt. (Allerdings ist dieser kein „Einfügepunkt“, sondern ein Vorfahr desselben.)
Suchen ohne Duplikate (rekursiv)
Der folgende Pseudocode Find illustriert die Arbeitsweise des Algorithmus für eine Suche, bei der in keinem Fall Duplikate in den Baum aufgenommen werden sollen. (Das ist letztlich unabhängig davon, ob die Ordnungsrelation Duplikate zulässt oder nicht.)
Die Funktion gibt einen Knoten und ein Vergleichsergebnis zurück. Dieses Paar stellt – außer beim Vergleichsergebnis „Equal“ – einen Einfügepunkt dar.
Find(t, s) {
t: binärerSuchbaum
s: Suchschlüssel
return Find0(t, s, t.root, Empty)
// zurück kommt ein Knoten und ein Vergleichsergebnis
}
Find0(t, s, x, d) {
t: Teilbaum
s: Suchschlüssel
x: Knoten
d: Vergleichsergebnis (Equal, LessThan, GreaterThan oder Empty)
if x ≠ null then {
if s = x.key then return (x, Equal) // Suchschlüssel s gefunden
if s < x.key
then return Find0(x, s, x.left, LessThan)
else return Find0(x, s, x.right, GreaterThan)
}
return (t, d) // Suchschlüssel s nicht gefunden
// zurück kommt (Knoten,Vergleichsergebnis) oder (Baum,Empty)
}
Bei dem in der Abb. 2 gewählten Beispiel würde Find beim Suchschlüssel s = den ersten Treffer, das obere , als Ergebnis zurückgeben.
Suchen ohne Duplikate (iterativ und mit Sentinel)
Die folgende Funktion FindWithSentinel hat genau dieselbe Funktionalität wie das obenstehende Find. Der Trick mit dem Wächterknoten oder Sentinel erspart pro Iterationsschritt eine Abfrage, und zwar die auf Abwesenheit des Kindknotens,[5][6] also (=Höhe) Abfragen. Sie wird hier iterativ programmiert in der Programmiersprache C vorgestellt.
Bemerkung: Da beim Ergebnis »gefunden« der Knoten, beim Ergebnis »nicht gefunden« aber der letzte Elterknoten gebraucht wird, kommen in der heißen Schleife zwei Variable alternierend zum Einsatz.
typedef struct NODE { // Knoten des binären Suchbaums
Node* lChild; // -> linker Kindknoten
Node* rChild; // -> rechter Kindknoten
int key; // Schlüssel
} Node;
typedef struct RESULT { // Ergebnisstruktur mit zwei Feldern
Node* resNod; // -> Ergebnisknoten
int resDir; // Vergleichsergebnis (Equal, LessThan, GreaterThan oder Empty)
} Result;
typedef struct BinarySearchTree { // Der binäre Suchbaum
Node* root; // -> Wurzel des Baums
} Bst;
Bst bst;
Node Sentinel, *sentinel = &Sentinel; // Der Wächterknoten und sein Zeiger
Sentinel.lChild = sentinel; Sentinel.rChild = sentinel;
// Initialisierung des leeren binären Suchbaums:
bst.root = sentinel; // Indikator, dass die Wurzel .root fehlt.
// Dieser Zeiger ist auch von den Einfüge- oder Löschfunktionen
// an den Stellen zu verwenden, wo es einen Kindknoten nicht gibt.
int FindWithSentinel(
Bst* t, // -> binärer Suchbaum
int sKey, // der Suchschlüssel
Result *r) // -> Ergebnisstruktur
{ Node *x, *y;
sentinel->key = sKey; // präpariere den Wächterknoten Sentinel
y = (Node*)t; // »Elter« der Wurzel
// Suchschleife:
for (x = t->root; sKey != x->key; ) {
if (sKey < x->key)
y = x->lChild; // ein echter oder der Wächter-Knoten
else
y = x->rChild; // dito
if (sKey == y->key) { // Schlüsselgleichheit
r->resNod = y; // Ergebnisknoten
goto Epilog;
}
if (sKey < y->key)
x = y->lChild; // dito
else
x = y->rChild; // dito
}
// Abbruch-Bedingung Schlüsselgleichheit: sKey == x->key
r->resNod = x;
x = y; // Elterknoten von r->resNod
Epilog:
if (r->resNod != sentinel) { // Der Ergebnisknoten r->resNod ist echt
// und zeigt auf einen Schlüssel mit Wert sKey.
r->resDir = Equal;
}
else { // Der Ergebnisknoten r->resNod ist unecht.
// x ist der »Elter« von r->resNod
r->resNod = x; // -> Ergebnisknoten (->Node oder ->Bst)
if (x != (Node*)t) { // x ist ein echter Knoten (->Node)
if (sKey < x->key) {
r->resDir = LessThan;
else
r->resDir = GreaterThan;
}
else // x ist der Baum (->Bst)
r->resDir = Empty;
}
return r->resDir;
// *r enthält (->Node,Vergleichsergebnis) oder (->Bst,Empty)
}
Suchen, wenn Duplikate zulässig
Sollen Einträge von Duplikaten in den Baum zugelassen sein, ist es vorteilhaft, die Suche nicht beim ersten besten gefundenen Knoten abzubrechen, sondern entweder auf der kleineren oder auf der größeren Seite bis zu den Blättern weiter zu suchen. Dies unterstützt eine gezielte Einfügung von Duplikaten und ist insbesondere dann interessant, wenn im Suchbaum nicht nur gesucht und gefunden werden soll, sondern u. U. auch traversiert wird. Der Einsatz der nachfolgenden Suchfunktionen beim Sortierverfahren Binary Tree Sort macht dieses Verfahren zu einem „stabilen“ (s. Stabilität (Sortierverfahren) mit erklärenden Beispielen).
Beim folgenden Pseudocode FindDupGE gibt der Benutzer die Richtung rechts vor, auf welcher Seite der Duplikate ein ggf. neues eingefügt werden soll. Bei einer Funktion FindDupLE mit dem gespiegelten Vergleich if s ≤ x.key würde ein neues Duplikat links von allen vorhandenen Duplikaten eingefügt werden.
FindDupGE(t, s, c) {
t: binärerSuchbaum
s: Suchschlüssel // FindDupGE: falls s ein Duplikat ist,
// soll es rechts (GE:≥) eingefügt werden.
c: Cursor { // Dieser Cursor enthält am Ende:
c.d: Richtung // (1) Left, Right oder Empty
c.n: Knoten // (2) Knoten oder Baum (nur bei Empty)
}
c.n = t // Für den leeren Baum return FindDupGE0(t.root, s, c, Empty) // zurück kommt ein Einfügepunkt im Cursor c }
FindDupGE0(x, s, c, d) {
x: Knoten
s: Suchschlüssel
c: Cursor
d: Richtung
if x ≠ null then {
c.n = x
if s ≥ x.key // Suchschlüssel s ≥ Knoten.Schlüssel?
then return FindDupGE0(x.right, s, c, Right) // ≥ (GE)
else return FindDupGE0(x.left, s, c, Left) // <
}
c.d = d // Setzen Einfüge-Richtung
return c
// zurück kommt ein Einfügepunkt im Cursor c
}
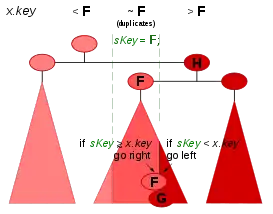
Das Paar (Knoten, Richtung) des vorigen Beispiels Find ist hier zu dem einen Objekt, genannt Cursor, zusammengefasst. Es ist ein reiner Ausgabeparameter, der den Einfügepunkt spezifiziert.
FindDupGE ist so gehalten, dass im Ergebnis-Cursor immer ein unmittelbarer Einfügepunkt geliefert wird. Aus dem Ergebnis ist aber nicht ohne Weiteres erkennbar, ob es sich um ein Duplikat handelt, da der Einfügepunkt nicht den gesuchten Schlüssel haben muss, selbst wenn dieser im Baum vorkommt. Dies hängt von der mehr oder minder zufälligen Anordnung der Knoten im Baum ab. Ist nämlich das rechteste Duplikat (im Beispiel der Abb. 2 das untere rechte ) kein Halbblatt nach rechts, dann ist es in der Hierarchie des Binärbaums ein Vorfahr seines rechten Nachbarn (im Beispiel ), der nun ein Halbblatt nach links ist und zusammen mit der Richtung „links“ denselben Einfügepunkt spezifiziert und also in diesem Fall das Resultat von FindDupGE darstellt.
Während bei Find alle 3 Wege der Vergleichsfunktion abgefragt werden, begnügt sich FindDupGE mit der Abfrage von deren 2[7].
Der nachfolgende Pseudocode FindDup kombiniert die Fähigkeiten von Find und FindDupGE, indem er sowohl ein Ergebnis über das Vorhandensein eines Suchschlüssels als auch einen Einfügepunkt für Duplikate liefert. Hierzu gibt der Benutzer eine Richtung d (links oder rechts) vor, auf welcher Seite der Duplikate ein ggf. neues eingefügt werden soll. Als Ergebnis kommt ein Paar (Knoten, Cursor) zurück, wobei Knoten angibt, ob und wo der Suchschlüssel gefunden wurde.
Der Vorschlag baut beispielhaft ein Objekt auf, das (in Analogie zum Beispiel zu den Datenbanken) Cursor genannt wird. Der #Cursor enthält den ganzen Pfad vom Ergebnisknoten bis zur Wurzel. Damit passt er zur nachfolgenden in-order-Traversierfunktion Next, eine Version, die ohne Zeiger zum Elterknoten auskommt. Die passende Datenstruktur für den Pfad ist der Stapelspeicher, engl. Stack, mit den Operationen push und pop.
Der etwas einfacheren Version der Funktion, bei der ein Zeiger zum Elter in jedem Knoten vorausgesetzt wird und deshalb der Cursor ohne Stack auskommt, entfallen die push- und clear-Aufrufe. Der Speicherbedarf für den Baum erhöht sich allerdings um einen Zeiger pro Knoten.
FindDup(t, s, c, d) {
t: binärerSuchbaum
s: Suchschlüssel
c: Cursor { // Dieser Cursor enthält am Ende:
c.d: Richtung // (1) Left, Right oder Empty
c.n: Knoten // (2) Knoten oder Baum (nur bei Empty)
// Die folgenden 2 nur, wenn die Elterknoten fehlen:
c.t: Baum // (3) Baum (enthält den Zeiger zur Wurzel)
c.p: Pfad // (4) Pfad vom Elter des Knotens zur Wurzel
}
d: Richtung // Falls s ein Duplikat ist, soll es ...
c.d = d // … auf dieser Seite eingefügt werden. c.t = t // initialisiere den Cursor clear(c.p) // initialisiere den Stack c.n = t // für den leeren Baum return FindDup0(t.root, s, c, Empty) // zurück kommt ein Knoten und ein Einfügepunkt im Cursor c }
FindDup0(x, s, c, d) {
x: Knoten
s: Suchschlüssel
c: Cursor
d: Richtung
if x ≠ null then {
push(c.p, c.n) // Elter c.n von x in den Stack
c.n = x // setze neuen Knoten im Cursor
if s = x.key then return FindDup1(x, s, c, c.d)
if s < x.key
then return FindDup0(x.left, s, c, Left)
else return FindDup0(x.right, s, c, Right)
}
c.d = d // Setzen Einfüge-Richtung
return (null, c) // Suchschlüssel s nicht gefunden
// zurück kommt null und ein Einfügepunkt im Cursor c
}
FindDup1(q, s, c, d) {
q: Knoten // letzter Knoten mit Equal
s: Suchschlüssel
c: Cursor
d: Richtung
x: Knoten
x = c.n.child[d]
if x ≠ null then {
push(c.p, c.n) // Elter c.n von x in den Stack
c.n = x // setze neuen Knoten im Cursor
if s = x.key
then return FindDup1(x, s, c, c.d) // x ist neuer Knoten mit Equal
else return FindDup1(q, s, c, 1 - c.d) // bei ≠ weiter in der Gegen-Richtung
}
c.d = d // Setzen Einfüge-Richtung
return (q, c)
// zurück kommt ein Duplikat und ein Einfügepunkt im Cursor c
}
FindDup ist so gehalten, dass im Ergebnis-Cursor immer ein unmittelbarer Einfügepunkt geliefert wird. Wenn der Suchschlüssel nicht gefunden wurde, wird im Feld Knoten der Nullzeiger zurückgegeben. Wenn der Suchschlüssel gefunden wurde, gibt FindDup das linkeste oder rechteste Duplikat, im Beispiel der Abb. 2 das rechteste Duplikat , als gefundenen Knoten zurück. Der Einfügepunkt kann mit dem gefundenen Knoten zusammenfallen; er kann aber auch sein unmittelbarer (im Beispiel der Abb. rechter) Nachbar sein, in welchem Fall er einen anderen Schlüssel (im Beispiel ) hat.
Im ersten Teil, FindDup0, werden alle 3 Wege der Vergleichsfunktion abgefragt; im zweiten Teil, FindDup1, wenn das Vorhandensein des Suchschlüssels positiv geklärt ist, nur noch deren 2.
Komplexität
Da die Suchoperation entlang eines Weges von der Wurzel zu einem Blatt verläuft, hängt die aufgewendete Zeit im Mittel und im schlechtesten Fall linear von der Höhe des Suchbaums ab (Komplexität ); im asymptotisch vernachlässigbaren besten Fall ist die Laufzeit bei Find konstant, bei FindDupGE und FindDup jedoch immer
Die Höhe ist im entarteten Fall so groß wie die Anzahl der vorhanden Elemente . Beim Aufbau eines Baumes, was einem Sortierlauf entspricht, muss im Extremfall jedes Element mit jedem verglichen werden – ergibt in summa Vergleiche.
Gewichtsbalancierte Suchbäume können im Mittel auf konstante Laufzeit kommen, verhalten sich jedoch linear im schlechtesten Fall. Höhen-balancierte Suchbäume haben eine Höhe von und ermöglichen so die Suche in garantiert logarithmischer Laufzeit. Der Aufbau eines Baumes kommt dann auf Vergleiche – das entspricht den besten Sortieralgorithmen.
Logarithmische Höhe gilt sogar im Durchschnitt für zufällig erzeugte Suchbäume, wenn die folgenden Bedingungen erfüllt sind:
- Alle Permutationen der einzufügenden und zu löschenden Elemente sind gleich wahrscheinlich.
- Bei Modifikationen des Baumes wird auf „asymmetrische“ Löschoperation verzichtet, d. h. die Abstiege bei den Löschungen nach links und die nach rechts halten sich im Mittel die Waage.
Suchtiefen und Pfadlängensummen
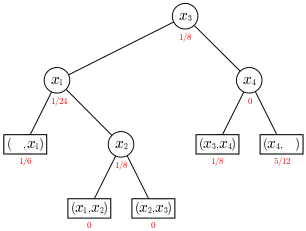
Sei eine Schlüsselmenge aus einem total geordneten Reservoir von Schlüsseln, seien ferner bzw. Häufigkeiten, mit denen auf das Element zugegriffen wird, wobei für resp. für . (Dabei seien und zusätzliche nicht zu gehörende Elemente mit der üblichen Bedeutung.) Das -Tupel
heißt Zugriffsverteilung[8] für die Menge , wenn alle sind. wird zur Zugriffswahrscheinlichkeitsverteilung, wenn ist.
Sei nun ein Suchbaum für die Menge mit einer Zugriffsverteilung , ferner sei die Tiefe des (inneren) Knotens und die Tiefe des (externen) Blattes (s. Abb. 3; jeweils #Terminologie der Abb. 1B). Wir betrachten die Suche nach einem Element . Wenn , dann vergleichen wir mit Elementen im Baum. Wenn , dann vergleichen wir mit Elementen im Baum. Also ist
die (mit der Zugriffsverteilung ) gewichtete Pfadlängensumme des Baumes ; ist eine Wahrscheinlichkeitsverteilung, dann ist die gewichtete Pfadlänge, die gewichtete Suchtiefe oder die mittlere Anzahl der benötigten Vergleiche. Die Abb. 3 zeigt einen Suchbaum , der mit einem Wert von optimal für die Zugriffsverteilung ist.
Sind alle und alle , dann ist mit die Summe der erforderlichen Vergleiche, wenn ein jeder der Knoten gesucht wird ( für erfolgreiche Suche). Sie steht zur so genannten internen Pfadlänge [9] in der Beziehung
- .
Für alle binären Suchbäume ist:
- ,
wobei die obere Grenze von der linearen Kette kommt und die untere von den vollständig balancierten Binärbäumen. Die Funktion ist stückweise linear, streng monoton steigend und konvex nach unten; in Formeln: Ist mit , dann ist .
Übrigens ist mit der Folge A001855 in OEIS.
Sind dagegen alle und alle , dann ist mit die Summe der notwendigen Vergleiche, um alle Blätter aufzusuchen ( für fehlend). wird auch als externe Pfadlänge [10] bezeichnet:
- .
Es gilt für alle Bäume :
- .[11]
- Beweis
Die Behauptung ist richtig für .
Sei ein Baum mit Knoten. Bei einem Knoten auf der Höhe fügen wir eine neue Kante und einen neuen Knoten hinzu. erhöht sich um und um , also wächst die Differenz um . ■
Die vollständig balancierten Binärbäume sind auch für die Zugriffsverteilung optimal, und es gilt für alle binären Suchbäume :
mit .
Übrigens ist mit der Folge A003314 in OEIS, und ist die Anzahl der externen Knoten (Blätter).
Traversierung
Traversierung (Querung) bezeichnet das systematische Erforschen der Knoten des Baumes in einer bestimmten Reihenfolge.
Es gibt verschiedene Möglichkeiten, die Knoten von Binärbäumen zu durchlaufen. Beim binären Suchbaum sind jedoch die sog. in-order- oder reverse in-order-Traversierungen die eindeutig bevorzugten, da sie die eingeprägte Ordnungsrelation wiedergeben.
In der Literatur finden sich fast ausschließlich (rekursive) Implementierungen, die nur über den ganzen Baum laufen – Beispiele in Binärbaum#Rekursive Implementierungen. Die Aktionen, die an den einzelnen Knoten auszuführen sind, sind dann in einer sog. Rückruffunktion (dort: callback) zu programmieren.
Eine Einzel-Traversierung, wie im nachstehenden Abschnitt vorgeschlagen, ist in der Praxis wesentlich flexibler einsetzbar.
Traversierung (Einzelschritt)
Der folgende Pseudocode Next gibt ausgehend von einem Knoten das nächste Element in ab- oder aufsteigender Reihenfolge zurück – eine iterative Implementierung. Der Vorschlag kommt ohne Zeiger zum Elterknoten aus. Dafür muss das Eingabeobjekt, hier #Cursor genannt, den ganzen Pfad vom aktuellen Knoten bis zur Wurzel enthalten, und dieser muss von der Next-Funktion auch entsprechend gepflegt werden, wenn Next in einer Schleife verwendet wird. Die passende Datenstruktur für den Pfad ist der Stapelspeicher, engl. Stack, mit den Operationen push und pop.
Die etwas einfachere Version der Funktion, bei der ein Zeiger zum Elter in jedem Knoten vorausgesetzt wird und deshalb der Cursor ohne Stack auskommt, ist beim Binärbaum aufgeführt. Der Speicherbedarf für den Baum erhöht sich allerdings um einen festen Prozentsatz.
Bei einer längeren Traversierung (mehreren Aufrufen von Next) wechseln sich Halbblätter und höherrangige Vorfahren ab.
Next(c) {
c: Cursor { // Dieser Cursor enthält:
c.d: Richtung // (1) EndOfTree oder Left, Right
c.n: Knoten // (2) Baum (nur bei EndOfTree) oder Knoten
c.t: Baum // (3) Baum (enthält den Zeiger zur Wurzel)
c.p: Pfad // (4) Pfad vom Elter des Knotens zur Wurzel
}
x,y: Knoten
x = c.n // Ausgangsknoten dieses Einzelschritts
d = c.d // gewünschte Richtung der Traversierung
y = x.child[d]
if y ≠ null then { // 1 Schritt in die gegebene Richtung
push(c.p, x) // Elter x von y in den Stack
d = 1 - d // spiegele Left <-> Right
// Abstieg in Richtung Blätter über Kinder in der gespiegelten Richtung
x = y.child[d]
while x ≠ null do {
push(c.p, y) // Elter y von x in den Stack
y = x
x = y.child[d]
}
c.n = y // Ergebnis: das nächste Halbblatt in Richtung c.d
return c // (Es ist Halbblatt auf seiner (1-c.d)-Seite.)
}
// Am Anschlag, deshalb Aufstieg zur Wurzel über die Vorfahren in der ...
do { // … c.d-„Linie“ (nur linke oder nur rechte)
y = x
x = pop(c.p) // Elter von y aus dem Stack
if x = c.t then { // y ist die Wurzel.
// Somit gibt es kein Element mehr in dieser Richtung.
c.n = c.t // Ergebnis: der Baum als Elter der Wurzel
c.d = EndOfTree // signalisiere das Ende der Traversierung
return c
}
} until y ≠ x.child[d]
// Es gab beim Aufsteigen einen Richtungswechsel:
c.n = x // Ergebnis: der erste Vorfahr in der gespiegelten Richtung
return c
}
Die Traversierung über den ganzen Baum umfasst pro Kante einen Abstieg und einen Aufstieg; der Aufwand bei Knoten ist also . Daher ist der Aufwand für eine Einzel-Traversierung im Mittel und amortisiert konstant und im schlechtesten Fall in O(h) mit h als der Höhe des Baums.
Ob die Abfrage auf Anwesenheit des Kindknotens als (x ≠ null) oder mit einem Wächterknoten (s. Abschnitt #Suchen ohne Duplikate (iterativ und mit Sentinel)) geschieht, macht keinen Unterschied – weder funktionell noch laufzeitmäßig. Da bei der Traversierung immer mit der Adresse x eines Knotens verglichen wird, ist durch die Präparation eines Wächterknotens mit einem Wert auch kein Vorteil zu erwarten.
Proximitäts-Suche
Jede Suchfunktion lässt sich mit der oben gezeigten Einzelschritt-Traversierung zu einer „Proximitäts“-Suche (engl. approximate match) kombinieren. Das ist eine Suche in der Nähe eines bestimmten Schlüssels, zum Beispiel auf „größer gleich“ (bzw. „kleiner gleich“).
Die obigen Suchfunktionen Find, FindDupGE und FindDup liefern im „ungleich“-Fall einen Einfügepunkt. Dieser enthält, wenn der Baum nicht leer ist, ein Element, das entweder das kleinste unter den größeren ist oder das größte unter den kleineren. Im ersteren Fall kann der Wunsch „größer gleich“ direkt befriedigt werden. Im letzteren Fall geht man zum nächsten Element in aufsteigender Reihenfolge, wenn es noch eines gibt, und gibt dieses zurück, denn es muss ein größeres sein. Die Logik für die gespiegelte Version liegt auf der Hand.
Ähnliche Funktionalität hat die Index Sequential Access Method.
Ein wichtiger Anwendungsfall ist die Abbildung mehrerer linear sortierter Schlüssel auf eine einzige lineare Ordnung mithilfe einer raumfüllenden Kurve, bspw. des Hilbert-Index. Hier ist möglicherweise die schlechtere Treffsicherheit des so gebildeten Schlüssels durch gute Nachbarschaftseigenschaften auszugleichen.
Einfügen
Es sei angenommen, dass die Navigation zum Einfügepunkt bereits erledigt ist. Einfügepunkt bedeutet einen Knoten und eine Richtung (rechts bzw. links). Ein unmittelbarer Einfügepunkt in einem binären Baum ist immer ein rechtes (bzw. linkes) Halbblatt (d. i. ein Knoten ohne rechten (bzw. linken) Kindknoten) zusammen mit dieser Richtung. (In der Sichtweise der Abb. 1B entspricht dies genau einem externen Knoten, deren Adressen sich dann aber alle verschieden sein müssen und die bspw. nicht als Sentinel implementiert sein dürfen.) Ein mittelbarer ist der unmittelbare Nachbar in der angegebenen Richtung und spezifiziert zusammen mit der Gegenrichtung dieselbe Stelle im Binärbaum – zum echten Einfügen muss aber die Einfügefunktion noch bis zu dem Halbblatt hinabsteigen, welches den unmittelbaren Einfügepunkt darstellt. Die obigen Funktionen Find, FindDupGE und FindDup liefern als Ergebnis einen (unmittelbaren) Einfügepunkt (Find nicht bei „Equal“).
Zum Einfügen lässt man den unmittelbaren Einfügepunkt (das Kind in der entsprechenden Richtung) auf das neue Element zeigen, damit ist dieses korrekt entsprechend der totalen Quasiordnung eingefügt. Die Komplexität der Einfügeoperation (ohne Suchvorgang) ist somit konstant. Wird eine Suchoperation hinzugerechnet (wie sehr häufig in der Literatur), dominiert diese die Komplexität.
Nach dem Einfügen ist das neue Element ein Blatt des Suchbaums.
Durch wiederholtes Einfügen von aufsteigend (oder absteigend) sortierten Schlüsseln kann es dazu kommen, dass der Baum zu einer linearen Liste entartet.
Löschen
Wie im Abschnitt Löschen des Artikels Binärbaum ausgeführt, gibt es verschiedene Möglichkeiten, einen Knoten aus einem binären Baum unter Erhaltung der bisherigen in-order-Reihenfolge zu entfernen. Da bei den Suchbäumen diese mit der Suchordnung zusammenfällt, bietet sich die folgende von T. Hibbard im Jahr 1962[12] vorgeschlagene Vorgehensweise an, die besonders geringe Änderungen an den Höhen der Teilbäume sicherstellt.
Der zu löschende Knoten sei mit bezeichnet.
- Hat zwei Kinder, gehe zu Schritt 4. Andernfalls ist ein Blatt oder hat nur ein einziges Kind. Dieses sei mit bezeichnet.
- War die Wurzel, dann wird zur neuen Wurzel.
Fertig! - Andernfalls setze Elter und mache an s Stelle und Kindesrichtung zum Kind von . Ist ein Knoten, wird zum neuen Elter von .
Fertig!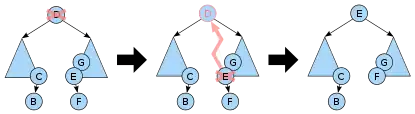 Abb. 4: Löschen eines Knotens mit 2 Kindknoten vermöge des rechten in-order-Nachfolgers von , des linkesten Knotens im rechten Kindbaum. (Bei unbalancierten Binärbäumen können die Knoten und Teilbäume sein.)
Abb. 4: Löschen eines Knotens mit 2 Kindknoten vermöge des rechten in-order-Nachfolgers von , des linkesten Knotens im rechten Kindbaum. (Bei unbalancierten Binärbäumen können die Knoten und Teilbäume sein.) - Hat zwei Kinder, navigiere im rechten Kindbaum von zum linkesten Knoten . Er ist der in-order-Nachfolger von und kann kein linkes Kind haben.[13][14]
- Setze Elter und Kindesrichtung, die links ist, wenn , sonst rechts.
- Kopiere Schlüssel und Daten von in den Knoten .[15]
- Setze rechtesKind. Es kann fehlen. Mache (an s Stelle) zum -Kind. Ist ein Knoten, wird neuer Elter von .
- Fazit[12]
- In einem binären Suchbaum, bei dem es nur auf die (in-order-)Reihenfolge ankommt, kann man beim Löschen den Zielknoten mit einem (seiner maximal zwei) in-order-Nachbarknoten vertauschen und, was die Baumstruktur mit ihren Zeigern etc. betrifft, diesen statt jenen aus dem Baum entfernen. Einer von beiden, der Zielknoten oder der Nachbarknoten, hat höchstens ein Kind.
Die Suchtiefe von -Kind, hier: , verringert sich um .
Durch wiederholtes Löschen kann es dazu kommen, dass der Baum zu einer linearen Liste entartet.
Wegen der unvermeidlichen Abstiege bis zu den Halbblättern ist die Komplexität der Löschoperation im schlechtesten Fall , wobei die Höhe des Baumes ist.
Sind Duplikate im Baum zugelassen, dann schlägt Mehlhorn vor, Elemente mit gleichem Schlüssel in der Last In – First Out-Disziplin abzuräumen.[16]
Implementierung

Die Abb. zeigt eine naheliegende Art der Speicherung. Sie entspricht in etwa den C-Strukturen:
struct node { // 1 Objekt = 1 Knoten
char key;
struct node * Kind_links;
struct node * Kind_rechts;
} object;
struct node * Kopf; // Zeiger auf die Wurzel
Zur besseren Unterscheidung der Objekte sind diese beziehentlich mit den Schlüsseln , , und versehen. Diese Schlüssel sind auch der Einfachheit halber als Ziel der Verweise genommen worden (anstelle von echten Speicheradressen). Wie üblich soll ein Zeigerwert 0 ausdrücken, dass auf kein Objekt verwiesen wird, es also kein Kind an dieser Stelle gibt.
Kopf
Da die Wurzel einer Löschung oder einer Rotation anheimfallen, somit den Baum nicht repräsentieren kann, muss diese Rolle von einer anderen Datenstruktur übernommen werden, die in der Literatur Kopf[17] genannt wird. Sie enthält den Zeiger zur Wurzel und fungiert als eine Art Elter der Wurzel.
Iterative Programmierung
In der Literatur werden die Operationen häufig in rekursiver Programmierung vorgestellt. Der Anwender hat aber mehrere Vorteile davon, wenn der Implementierer die vom Aufschreiben her eleganten Rekursionen durch simple Iterationen ersetzt hat, da dadurch (Höhe) Prozeduraufrufe und -rücksprünge eingespart werden und der Speicherbedarf für den Programm-Stapelspeicher konstant gehalten wird. Es geht aber nicht nur um Ressourcenschonung. Bei der Traversieroperation wird dadurch beispielsweise die Programmierung der Anwendung wesentlich vereinfacht.[18] Für das Aufbewahren des Rückwegs zu Wurzel und Kopf, der beim Traversieren, aber auch häufig bei Modifikationen zur Aufrechterhaltung der Bauminvarianten (AVL- oder Rot-Schwarz-Kriterium), gebraucht wird und der bei der rekursiven Programmierung neben anderem im Programmstapelspeicher steckt, muss dann ein anderes, explizites Konstrukt gewählt werden, welches sich im Cursor (siehe unten) subsumieren lässt.
Dadurch wird eine Trennung der modifizierenden Operationen von der Navigation möglich.
Trennung der navigierenden von den modifizierenden Operationen
Einfüge- und Löschoperation sind sinnvollerweise von der Suchoperation zu trennen, wenn zum Einfügepunkt beziehungsweise Knoten auch auf andere Weise als mit der Standardsuchoperation navigiert werden soll, beispielsweise mittels eines Querschritts oder mithilfe einer zweiten Suchstruktur für dasselbe Element wie in der #Mehrere Zugriffspfade.
Diese Modularisierung der Navigations- von den modifizierenden Operationen setzt einen gegebenenfalls unterlogarithmischen (sprich: konstanten) Aufwand der letzteren frei, denn ein Aufstieg bis zur Wurzel ist beispielsweise bei AVL-Baum und Rot-Schwarz-Baum nur in Ausnahmefällen erforderlich. In Anwendungen mit starkem sequentiellem Anteil kann sich das positiv auf die Laufzeit auswirken.
Cursor
Beim Suchen wird ein Paar (Knoten, Richtung) erzeugt, welches geeignet ist, beim Einfügen den Einfügepunkt zu spezifizieren. Beim Löschen wird der zu löschende Knoten durch die Komponente Knoten bezeichnet, und die Komponente Richtung kann angeben, wohin der Cursor nach der Löschung fortschreiten soll. Beim Traversieren gibt Knoten den Ausgangspunkt und Richtung die gewünschte Richtung der Navigation an, um im Ergebnis wieder bei einem solchen Paar anzukommen. Damit erzeugen und/oder verbrauchen alle wichtigen Operationen ein Konstrukt, das (in Analogie zum Beispiel zu den Datenbanken) Cursor genannt wird.[19]
Die Größe des Cursors hängt entscheidend davon ab, ob die Knoten einen Zeiger zum Elter enthalten oder nicht.
- Elterzeiger vorhanden: Ein Paar (Knoten, Richtung) stellt einen vollwertigen Cursor dar.
Ein Cursor wird nach einer Operation dann und nur dann ungültig, wenn es sich um eine Löschung handelt, und der Knoten des Cursors das Ziel der Löschung ist.
Mit dem prozentualen Aufschlag auf den Speicherbedarf für die Datenstruktur erkauft man sich auf jeden Fall eine prozentuale Einsparung an Laufzeit, da der Rückweg zu Wurzel und Kopf immer schon gesichert ist. - Zeiger zum Elterknoten nicht vorhanden („Cursor mit Stapel“): Zusätzlich zum Paar (Knoten, Richtung) muss der Pfad vom Knoten zu Wurzel und Kopf im Cursor gehalten werden.[20] Die Länge des Cursors entspricht damit der maximalen Höhe des Baums. Diese ist entweder von sich aus ausreichend beschränkt (vorgerechnetes Beispiel AVL-Baum), oder der Stapelüberlauf löst eine Reorganisation des Baums oder ein abnormales Ende aus.
Bei allen Operationen ist der Zugriff zum Elterknoten über den Stapel im Cursor geringfügig teurer als über den Elterzeiger. Soll der Pfad im Cursor auch nach einer modifizierenden Operation gültig gehalten werden (beispielsweise für sequentielle Einfügungen oder Löschungen), kommt noch ein zusätzlicher prozentualer Aufschlag hinzu. Dies kann so aber nur für einen Cursor, den Eingabecursor, erbracht werden.
Benötigt eine Anwendung mehrere Cursor für ein und denselben Suchbaum und über Änderungen an ihm hinweg, dann kann das Aufrechterhalten der Konsistenz der Cursor mit Stapel (zum Beispiel durch erneutes Suchen) so aufwändig werden, dass es wirtschaftlicher ist, dem Baum Elterzeiger zu spendieren.
Mehrere Zugriffspfade
Als Beispiel für eine Anwendung mit 2 Zugriffspfaden sei ein klassisches Speichermanagement gebracht. Elemente der Datenstruktur sind die freien Speicherblöcke mit den Attributen (Feldern) Ort und Größe. Für jedes der beiden Felder gebe es eine Suchstruktur, bei Ort ohne Duplikate. Da bei Größe jedoch Duplikate unvermeidlich sind, empfiehlt sich ein lexikographisch zusammengesetzter Schlüssel (Größe,Ort). Beim Akquirieren wird ein Block von Mindestgröße gesucht, ausgetragen und ein Rest, falls vorhanden, wieder eingetragen. Bei der Speicherrückgabe wird nach Ort gesucht, auf Konfliktfreiheit mit den Nachbarblöcken geprüft (ebenfalls ein Beispiel für die Nützlichkeit der Querschritts) und der zurückzugebende Block gegebenenfalls mit diesen verschmolzen. Alle Veränderungen müssen auf beiden Suchstrukturen durchgezogen werden. Sind Elterzeiger vorhanden, dann erspart das Hangeln von der einen Suchstruktur zur anderen einen Suchvorgang.
Anwendungen
Wie Ben Pfaff[21] zeigt, decken die dynamischen Suchbaumstrukturen AVL-Baum, Rot-Schwarz-Baum und Splay-Baum dieselben wesentlichen Funktionen ab. Große Unterschiede stellt er im Laufzeitverhalten fest, wobei der AVL-Baum in Median und Mittelwert am besten abschneidet.
In der Informatik haben die dynamischen Suchbaumstrukturen einen großen Einsatzbereich als grundlegende Hilfsmittel bei:
- Duplikatunterdrückung, Deduplikation, Duplikaterkennung
- Elementare Mengenoperationen wie Durchschnittsbildung und Vereinigung
- Standard Template Library (STL)
Bei Ben Pfaff[21] finden sich systemnahe Anwendungen (alle unter ×86-based Linux):
- Verwaltung von Virtual Memory Areas (VMAs) unter Einschluss von range queries zur Feststellung des Überlappens von existierenden VMAs (S. 4)
- Eindeutige Kennzeichnung von IP-Paketen (S. 7)
Ferner:
- Liste der Variablen in einem Programm, die ein Interpreter zu pflegen hat: der Interpreter muss jederzeit in der Lage sein zu entscheiden, ob einer Programmvariablen momentan ein Wert zugewiesen ist und gegebenenfalls welcher. Ähnliches gilt für einen Compiler.
- Binary Tree Sort (Sortieren durch Einfügen)
- In #Mehrere Zugriffspfade ein klassisches Speichermanagement.
Effiziente Massen- und Mengenoperationen aufbauend auf der JOIN-Operation
Mithilfe einer JOIN-Operation (Konkatenation (Verkettung)) von Binärbäumen sind (hoch parallele) Algorithmen für Mengenoperationen beschrieben[22] worden. Dabei sind die (endlichen) Mengen und Abbildungen dargestellt durch selbst-balancierende Binärbäume, und zwar insbesondere Rot-Schwarzbäume, AVL-Bäume, Binärbäume mit beschränkter Balance oder Treaps.
Die Algorithmen sind open source als PAM (Parallel Augmented Maps)[23] in C++ auf GitHub verfügbar.
Auswahlkriterien
Das binäre Suchen im Array kann als eine Art Vorläufer der binären Suchbäume angesehen werden. Da es sich bei Einfügungen und Löschungen linear verhält und dann auch die Speicherverwaltung seines Arrays sorgfältig überlegt werden muss, wird es in der Praxis fast nur für statische, vorsortierte Tabellen eingesetzt. Sind also Einfügungen oder Löschungen für die Anwendung wichtig, sind die Binärbäume geeigneter. Bezüglich Suchzeit und Speicher verhalten sich binäres Suchen im Array und höhenbalancierte binäre Suchbäume asymptotisch gleich.
Obwohl rein zufällige binäre Suchbäume sich im Mittel logarithmisch verhalten, garantiert ein binärer Suchbaum ohne irgendeine Vorkehrung, die einer Entartung entgegenwirkt, keineswegs eine unterlineare Laufzeit. Entartungen können systematisch vorkommen, zum Beispiel wenn ein Programmierer massenhaft nahe benachbarte Sprungmarkennamen vergibt.
Es gibt jedoch sehr viele Konzepte, die dazu entwickelt wurden, eine ausreichende Balance sicherzustellen. Hierbei stehen sich immer Aufwand und Ertrag gegenüber. Zum Beispiel ist der Aufwand, einen binären Suchbaum ständig vollständig balanciert zu halten, so hoch, dass sich das nur bei Anwendungen lohnen dürfte, deren Laufzeit in extremer Weise vom Suchen dominiert wird.
Ein wichtiges Kriterium für die Auswahl ist, ob der Binärbaum statisch ist, und so ein einmaliger optimaler Aufbau ausreicht, oder ob verändernde Operationen wie Einfügen und Löschen wichtig sind. Für erstere kommen gewichtete Suchbäume in Betracht, worunter auch der Bellman-Algorithmus. Bei letzteren sind höhen-balancierte Suchbäume wie der AVL-Baum und der Rot-Schwarz-Baum, aber auch Splay-Bäume von Interesse.
Eine Gegenüberstellung von Komplexitäten verschiedener Suchalgorithmen finden sich im Artikel Suchbaum; Laufzeitmessungen anhand realistischer Beispiele sind zu finden bei Pfaff 2004b.
Bei diesen Überlegungen wurde generell angenommen, dass der ganze Baum im Arbeitsspeicher (Hauptspeicher) untergebracht ist. Spielen Zugriffe zu externen Medien eine Rolle, kommen ganz andere Kriterien hinzu. Schon der B-Baum, der solche Gesichtspunkte berücksichtigt, ist zwar ein Suchbaum, aber nicht mehr binär.
Historisches
Die im Abschnitt Motivation erwähnte, sehr bekannte Suchstruktur Binäre Suche im Array gilt als Vorläufer der dynamischen Suchbaumstrukturen. Als naheliegende Umsetzung des Nachschlagens in einem (sortierten) Wörterbuch, dürfte sie mehrfach und ohne Kenntnis anderer Implementierungen entwickelt und implementiert worden sein. Im dynamischen Anwendungsfall kann sie aber mit den neueren Entwicklungen nicht mithalten, obwohl sie im statischen Fall eine hervorragende Lösung ist. Es gibt Makros, die einen Compiler veranlassen, zu einer gegebenen (sortierten) Tabelle von (Schlüssel, Werte)-Paaren Quelltext für eine iterierende oder schleifenlose binäre Suche zu erzeugen.
Im Jahr 1962 erschien zum ersten Mal eine dynamische Suchbaumstruktur in Form des AVL-Baums. Seine Erfinder sind die genannten sowjetischen Mathematiker Georgi Adelson-Welski und Jewgeni Landis. Ihr Beitrag im Journal Doklady Akademii Nauk SSSR wurde noch im selben Jahr ins Englische übersetzt. Die Übersetzung trägt (wie entsprechend das Original) den sehr ehrgeizigen Titel „An algorithm for the organization of information“. Die Bezeichnung AVL-Baum findet sich in dieser Übersetzung nicht.
Im Jahr 1970 veröffentlichte Rudolf Bayer[24] seine erste Arbeit über den B-Baum. Er ist kein Binärbaum, unterstützt heterogene Speicher, beispielsweise Hauptspeicher und Hintergrundspeicher, und wird bei Datenbanksystemen eingesetzt.
Danach folgte im Jahr 1972 zunächst unter dem Namen „symmetric binary B-tree“ der Rot-Schwarz-Baum von Rudolf Bayer.[25] Ihm war die Balance-Regel des AVL-Baums zu streng. Eine Umbenennung erfolgte 1978 von Leonidas Guibas und Robert Sedgewick[26] in das heute übliche „red–black tree“, später auch „RB tree“.
Splay-Bäume wurden im Jahr 1985 von Daniel Sleator und Robert Tarjan[27] unter dem Namen „Self-Adjusting Binary Search Trees“ vorgestellt. Sie sind noch dynamischer als die vorgenannten, indem sie sich auch bei Suchoperationen verändern.
Eine grobe Gegenüberstellung dynamischer Suchbäume findet sich im
Literatur
- Donald E. Knuth: The art of computer programming. Volume 3: Sorting and Searching. 3. Auflage. Addison-Wesley, 1997, ISBN 0-201-89683-4.
- Kurt Mehlhorn: Datenstrukturen und effiziente Algorithmen. Teubner, Stuttgart 1988, ISBN 3-519-12255-3.
- Kurt Mehlhorn, Peter Sanders: Algorithms and Data Structures. The Basic Toolbox. Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-77977-3, doi:10.1007/978-3-540-77978-0.
Weblinks
- Ben Pfaff: An Introduction to Binary Search Trees and Balanced Trees. (PDF, gzip; 1675 kB) 2004 (englisch).
- Ben Pfaff: Performance Analysis of BSTs in System Software. (PDF; 316 kB) Stanford University, 2004 (englisch).
Einzelnachweise und Anmerkungen
- Gibt es keine Werte, sondern nur Schlüssel, so ist das zugrunde liegende Modell das der endlichen Menge, und die Fragestellung reduziert sich darauf, ob ein gegebener Schlüssel in der Menge vorhanden ist oder nicht. Es ist also die Indikatorfunktion der Menge zu realisieren.
- Die Sichtweise der Abb. 1B findet sich beispielsweise bei #Knuth und im Artikel Rot-Schwarz-Baum. Eine explizite Gegenüberstellung der beiden Sichtweisen gibt #Pfaff 2004a, p. 30 „4.1.1 Aside: Differing Definitions“. Dort wird die Sichtweise der Abb. 1A als die des Implementierers bezeichnet.
- #Mehlhorn 1988 S. 296
- deren Erfüllung der Relationsgesetze die Software nicht nachprüfen kann
- #Pfaff a § 23
- #Mehlhorn 2008
- wie
locateLocallyin #Mehlhorn 2008 S. 150 - nach #Mehlhorn 1988 S. 147
- internal path length bei #Knuth pp. 399–400
- external path length bei #Knuth pp. 399–400
- bei #Knuth.
- zitiert nach: Robert Sedgewick, Kevin Wayne: Algorithms Fourth Edition. (PDF) (Seite nicht mehr abrufbar, Suche in Webarchiven) Info: Der Link wurde automatisch als defekt markiert. Bitte prüfe den Link gemäß Anleitung und entferne dann diesen Hinweis. Pearson Education, 2011, ISBN 978-0-321-57351-3, S. 410 (englisch) abgerufen am 25. März 2018
- Genauso gut kann man im linken Kindbaum von zum rechtesten Knoten navigieren, der der in-order-Vorgänger von ist und kein rechtes Kind haben kann.
Bei einheitlicher Wahl der Seite des Abstiegs wurde die Ausbildung einer gewissen Asymmetrie der Balancierung festgestellt, so dass manche Autoren, z. B. Mehlhorn, das Abwechseln der Seite des Abstiegs empfehlen. - Wenn die Knoten keinen Elterzeiger haben und der Weg zurück zur Wurzel über einen Stapelspeicher realisiert wird, ist derselbe in beiden Fällen beim Abstieg fortzuschreiben.
- Die gewählte Sprechweise dient nur der leichteren Verständlichkeit. Natürlich muss ein generisches Softwarepaket von Benutzerdaten unabhängig bleiben und umgekehrt vorgehen, nämlich die ihm nicht notwendigerweise bekannten Benutzerdaten des Knotens unberührt lassen und mit allen zum binären Suchbaum gehörigen Verbindungen des Knotens ausstatten, sowie alle auf zeigenden Zeiger auf zeigen lassen. Dazu gehört, dass, falls die Wurzel war, der Knoten zur neuen Wurzel wird.
- So in Exercise 7.10. in #Mehlhorn 2008 S. 155. Die obigen Funktionen
FindDupGEundFindDupLEunterstützen dieses, wenn beim Einfügen und Löschen dieselbe genommen wird. Wird die jeweils andere Funktion genommen, bspw. beim EinfügenFindDupGEund beim LöschenFindDupLE, dann implementiert man eine First In – First Out-Disziplin. - „Header node“ und „HEAD“ bei Donald E. Knuth: The Art of Computer Programming, Band 3, Sorting and Searching, 2. Auflage, Addison-Wesley, 1998, S. 462; totum pro parte „tree data structure“ bei Ben Pfaff: An Introduction to Binary Search Trees and Balanced Trees. Free Software Foundation, Inc. Boston 2004.
- Siehe dazu Traversierung (mit Codebeispielen) und Ben Pfaff: An Introduction to Binary Search Trees and Balanced Trees. Free Software Foundation, Inc. Boston 2004, S. 47 „4.9.2 Traversal by Iteration“.
- Ben Pfaff gibt einem Objekt mit sehr ähnlicher Funktionalität den Namen „traverser“ und offeriert für Suchen, Einfügen und Löschen eine Standard- und eine Traverser-Variante. (#Pfaff 2004a, p. 15 „2.10 Traversers“)
- „auxiliary stack“ bei #Knuth (p. 461), der beim AVL-Baum die Einfügung aber anderweitig löst.
- Ben Pfaff: Performance Analysis of BSTs in System Software. Stanford University 2004.
- Guy Edward Blelloch, Daniel Ferizovic, Yihan Sun: Just Join for Parallel Ordered Sets. Hrsg.: ACM (= Symposium on Parallel Algorithms and Architectures, Proc. of 28th ACM Symp. Parallel Algorithms and Architectures (SPAA 2016)). 2016, ISBN 978-1-4503-4210-0, S. 253–264, doi:10.1145/2935764.2935768, arxiv:1602.02120.
- Yihan Sun, Daniel Ferizovic, Guy E. Blelloch: PAM: parallel augmented maps. Hrsg.: ACM (= ACM SIGPLAN Notices). 23. März 2018, ISSN 0362-1340, S. 290–304, doi:10.1145/3200691.3178509 (acm.org).
- Rudolf Bayer, Edward M. McCreight: Organization and Maintenance of Large Ordered Indices. Mathematical and Information Sciences Report No. 20. Boeing Scientific Research Laboratories, 1970.
- Rudolf Bayer: Symmetric binary B-Trees: Data structure and maintenance algorithms. In: Acta Informatica. 1, Nr. 4, 1972, S. 290–306. doi:10.1007/BF00289509.
- Leonidas J. Guibas, Robert Sedgewick: A Dichromatic Framework for Balanced Trees. In: Proceedings of the 19th Annual Symposium on Foundations of Computer Science ., S. 8–21. doi:10.1109/SFCS.1978.3
- Daniel D. Sleator, Robert Tarjan: Self-Adjusting Binary Search Trees. In: Journal of the ACM (Association for Computing Machinery). Band 32, Nr. 3, 1985, S. 652–686, doi:10.1145/3828.3835 (cs.cmu.edu [PDF; 6,1 MB]).