AVL-Baum
Der AVL-Baum ist eine Datenstruktur in der Informatik. Es handelt sich dabei um einen binären Suchbaum mit der zusätzlichen Eigenschaft, dass sich an jedem Knoten die Höhe der beiden Teilbäume um höchstens eins unterscheidet.[1] Diese Eigenschaft lässt seine Höhe nur logarithmisch mit der Zahl der Schlüssel wachsen und macht ihn zu einem balancierten binären Suchbaum. Die maximale (und mittlere) Anzahl der Schritte (Vergleiche), die nötig sind, um An- oder Abwesenheit eines Schlüssels festzustellen, hängt direkt mit der Höhe zusammen. Ferner ist der maximale Aufwand für Operationen zum Einfügen und Entfernen eines Schlüssels proportional zur Höhe des Baums und damit ebenfalls logarithmisch in der Zahl der Schlüssel; der mittlere Aufwand ist sogar konstant, wenn das Positionieren auf das Zielelement nicht mitgerechnet wird.
| AVL-Baum | ||
|---|---|---|
| Komplexität | ||
| Platz | ||
| Operation | im Mittel | Worst Case |
| Suchen | ||
| Querschritt | ||
| Min, Max | ||
| Einfügen | † | |
| Löschen | † | |
| Verketten | ||
| Spalten | ||
| Knoten im Baum † ohne Navigation | ||
| Platz- und Zeit-Komplexitäten | ||
Viele Operationen, insbesondere die Navigationsoperationen, sind direkt von den binären Suchbäumen zu übernehmen. Bei den modifizierenden Operationen jedoch muss das AVL-Kriterium beobachtet werden, womit auf jeden Fall kleine Anpassungen verbunden sind, die bis zu Höhenkorrekturen durch sogenannte Rotationen reichen können.
Der AVL-Baum ist benannt nach den sowjetischen Mathematikern Georgi Maximowitsch Adelson-Velski und Jewgeni Michailowitsch Landis, die die Datenstruktur im Jahr 1962 vorstellten.[2] Damit ist der AVL-Baum die älteste Datenstruktur für balancierte Bäume.
Motivation
Suchbäume – und damit auch die AVL-Bäume – sind Lösungen des sogenannten „Wörterbuchproblems“. Eine prinzipielle Erläuterung findet sich im Abschnitt Motivation im Artikel Binärer Suchbaum.
Den Suchbäumen gemeinsam ist, dass sie Dynamik unterstützen, das heißt, dass Einfügen und/oder Löschen von Elementen wichtig ist. Da bei diesen Operationen die Gefahr besteht, dass die Balance des Baums verloren geht, wurden verschiedene Balance-Kriterien für Binärbäume entwickelt. Bei den meisten sind die Aufwände für das Suchen, Einfügen und Löschen zumindest im Mittel logarithmisch, wenn auch mit unterschiedlichen konstanten Faktoren.
Beim AVL-Baum wird die Balance über die Höhe definiert, er ist ein höhen-balancierter binärer Suchbaum.
Das AVL-Kriterium
Als den Balance-Faktor[3] eines Knotens resp. Teilbaums[Anm 1] in einem Binärbaum bezeichnet man die Höhendifferenz
wobei die Höhe des Baums , und der linke, der rechte Kindbaum von ist.[Anm 3] Ein Knoten mit wird als höhengleich oder ausgewogen, einer mit als links- und einer mit als rechtslastig bezeichnet.
Ein binärer (Such-)Baum ist genau dann ein AVL-Baum, wenn die AVL-Bedingung
an jedem Knoten eingehalten wird.[Anm 4]
Eigenschaften
Diese Definition beschränkt die Höhe [Anm 5] eines AVL-Baums mit Knoten (Schlüsseln) durch die Ungleichung[4]
mit , und (Zahl des goldenen Schnitts).
Die untere Schranke kommt vom vollständigen Binärbaum (bei dem bis auf die unterste Ebene alle Ebenen komplett sind); die obere vom Fibonacci-Baum, der bei gegebener Höhe einen AVL-Baum mit kleinster Knotenanzahl darstellt – also bei gleicher Knotenzahl die größte Höhe hat – somit (in Bezug auf die Höhe) am schlechtesten balanciert ist. Dabei ist die Höhe gemittelt über alle zufälligen Einfügungen in einen AVL-Baum vorgegebener Größe näher bei der unteren als bei der oberen Grenze des Intervalls.[5]
Datenstruktur
Werden der Datenstruktur AVL-Baum Operationen zum Zugriff und zur Verwaltung beigegeben, so werden diese nur dann als zugehörig angesehen, wenn sie die AVL-Eigenschaft aufrechterhalten. So erweitert wird die Datenstruktur zu einem Abstrakten Datentyp (ADT). Bei Suchbäumen gibt es im Englischen dafür auch die Charakterisierung als self-balancing tree.
Operationen
Die wichtigsten Operationen bei den Suchbäumen – und damit beim AVL-Baum – sind: Suchen einerseits sowie Einfügen und Löschen andererseits. Mit der Eigenschaft, dass alle diese Operationen im schlechtesten Fall (Worst Case) logarithmische Komplexität haben, gehört der AVL-Baum zu den höhenbalancierten binären Suchbäumen.
Navigieren
Die Navigationsoperationen, das sind die verschiedenen Suchoperationen, das Traversieren und Iterieren, Aufsuchen erstes oder letztes Element und ähnliche, lassen den Baum unverändert und funktionieren im Prinzip auf jedem binären Suchbaum. Die dortigen Angaben zur Komplexität gelten genauso für AVL-Bäume, mit der Präzisierung, dass die Höhe des AVL-Baums sich logarithmisch zur Anzahl der Knoten verhält.
Das Suchen (englisch: find, search, lookup oder locate) eines Elements anhand seines Schlüssels ist die wichtigste unter den Navigationsoperationen. Die Höhen-Balancierung des AVL-Baums versucht, auf diese Operation hin zu optimieren. Sie ermöglicht einen sogenannten direkten Zugriff (im Gegensatz zum sequentiellen Zugriff der Traversierung). Sie wird in der Regel als vorausgehende Operation sowohl beim Einfügen als auch beim Löschen eingesetzt.
Das Suchen setzt eine totale Quasiordnung auf der Menge der Schlüssel voraus, die am flexibelsten durch eine Vergleichsfunktion bereitgestellt wird.
Das mittlere Laufzeitverhalten des Suchens in einem binären Suchbaum wird durch die Pfadlängensumme wiedergegeben, welche geteilt durch die Knotenzahl die mittlere Suchtiefe definiert. Diese verhält sich beim AVL-Baum proportional zur optimalen Suchtiefe – mit einem Proportionalitätsfaktor nur wenig größer als 1.[Anm 6]
Einfügen (Eintragen)
Es sei angenommen, dass die Navigation zum Einfügepunkt bereits erfolgt ist. Ein Einfügepunkt ist ein externes Blatt[6] und liegt ganz links oder ganz rechts oder zwischen 2 internen (und Schlüssel tragenden) Knoten, kann also auf jeden Fall durch einen (internen) Knoten zusammen mit einer Richtung (links oder rechts) spezifiziert werden. Die Knoten ganz links oder ganz rechts sind immer (Halb-)Blätter, wie auch von 2 Nachbarknoten wenigstens einer ein (Halb-)Blatt ist. Ein solcher Knoten sei – zusammen mit der entsprechenden Richtung – als der unmittelbare Einfügepunkt bezeichnet. So wird er auch von einer nicht erfolgreichen Suchoperation geliefert.
Zur Einfügung (englisch: insert oder add) wird der Knoten mit dem neuen Schlüssel als Blatt am Einfügepunkt eingehängt – mit anderen Worten: das externe Blatt wird zum internen Blatt. Die Höhe des aus diesem Blatt bestehenden Teilbaums erhöht sich von 0 auf 1. Für die Reparatur des Baumes oberhalb des Einfügepunktes gibt es 2 verschiedene Vorgehensweisen:
- Man geht den Pfad der Elterknoten zurück bis u. U. zur Wurzel („retracing“ in der englischen Literatur). Hier muss ein Stapelspeicher (bei rekursiver Programmierung meist der Programm-Stapelspeicher) vorher mit den Knoten im Pfad gefüllt worden sein.
- Man hat sich beim Suchen im Abstieg einen (dann den letzten, tiefsten) nicht-ausgewogenen (also links- oder rechtslastigen) Knoten gemerkt („Top-Down-Strategie“).[7] Die finale Reparatur ist dann ein zweiter Abstieg ab diesem Elterknoten. Man kann für dieses Teilstück die Vergleiche wiederholen oder man hat sich die Vergleichsergebnisse vorher in einem Stapelspeicher (mit einem Bit pro Eintrag) gemerkt.[8]
Wir zeigen hier die „einfachere“ Variante, die der Abfolge bei rekursiver Programmierung entspricht. Beim Aufstieg zum Elterknoten, und später bei jedem weiteren Aufstieg, gibt es entsprechend der 3 Werte des ursprünglichen Balance-Faktors dieses Knotens 3 Möglichkeiten für den neuen (temporären) Balance-Faktor:
- Wird der Balance-Faktor zu 0, dann kommt man von einem Kindbaum, der vorher niedriger war, und die Höhe des Knotens ändert sich nicht – mit der Folge, dass oberhalb alle Balance-Faktoren bleiben können, wie sie sind, und das AVL-Kriterium für den ganzen Baum erfüllt ist.
- Wird der Balance-Faktor zu ±1 (er muss vorher 0 gewesen sein), erhöht sich die Höhe des Teilbaums um 1, und die Überprüfung der Balance-Faktoren oberhalb muss weitergehen.
- Wird auf einer Ebene der Balance-Faktor zu ±2, muss der Teilbaum rebalanciert werden (siehe Rebalancierung weiter unten). Danach hat bei einer Einfügeoperation der Teilbaum die gleiche Höhe wie vorher – mit der Folge, dass oberhalb alle Balance-Faktoren bleiben können, wie sie sind, und das AVL-Kriterium für den ganzen Baum auch schon erfüllt ist.
Das Einfügen des -ten Knotens in einen AVL-Baum mit Knoten hat im schlechtesten Fall (mit oder ohne Suchen) logarithmischen Aufwand, beispielsweise wenn jede Ebene bis hinauf zur Wurzel überprüft werden muss. Da aber hierfür die Wahrscheinlichkeit von Ebene zu Ebene nach oben hin exponentiell abnimmt, ist der reine Modifikationsaufwand (Ändern von Balance-Faktoren und Rotationen) beim Einfügen im Mittel konstant.[Anm 7] Es kann sogar gezeigt werden, dass der Modifikationsaufwand in einem reinen Einfügeszenario amortisiert konstant ist.[9]
| Code-Schnipsel |
|
Bei der Einfügung des neuen Knotens Z als Kind von X wächst die Höhe dieses Teilbaums Z von 0 auf 1. Schleifeninvariante bei der Einfügung Die Höhe des Teilbaums Z erhöht sich um 1. Er ist in AVL-Form. // Schleife vom Blatt bis möglicherweise zur Wurzel:
for (X = Z->parent; X != null; X = Z->parent) {
if (Z == X->childR) { // Der rechte Teilbaum ist es, der höher wird.
if (X->BF <= 0) { // X ist nicht rechtslastig
if (X->BF < 0) { // X ist linkslastig
X->BF = 0; // Z’s Höhenzunahme aufgefangen bei X
break; // Verlassen der Schleife
}
X->BF = +1;
Z = X; // Height(Z) wird höher um 1
continue;
}
else { // X ist rechtslastig
// ===> X->BF temporär == +2
// ===> Rebalancierung erforderlich
G = X->parent; // Retten X->parent vor Rotation
if (Z->BF < 0) // Rechts-Links-Situation (s. Abbildung 3)
N = rotate_RightLeft(X,Z); // Doppelrotation: Right(Z) dann Left(X)
else // Rechts-Rechts-Situation (s. Abbildung 2)
N = rotate_Left(X,Z); // Einfachrotation Left(X)
}
}
else { // Z == X->childL: der linke Teilbaum wird höher
if (X->BF >= 0) { // X ist nicht linkslastig
if (X->BF > 0) { // X ist rechtslastig
X->BF = 0; // Z’s Höhenzunahme aufgefangen bei X
break; // Verlassen der Schleife
}
X->BF = –1;
Z = X; // Height(Z) wird höher um 1
continue;
}
else { // X ist linkslastig
// ===> X->BF temporär == –2
// ===> Rebalancierung erforderlich
G = X->parent; // Retten X->parent vor Rotation
if (Z->BF > 0) // Links-Rechts-Situation
N = rotate_LeftRight(X,Z); // Doppelrotation: Left(Z) dann Right(X)
else // Links-Links-Situation
N = rotate_Right(X,Z); // Einfachrotation Right(X)
}
}
// Nach der Rotation die Anpassung der Verknüpfung N<->G:
// N ist die neue Wurzel des rebalancierten Teilbaums
// Höhe ändert sich nicht: Height(N) == alte Height(X)
N->parent = G;
if (G != null) {
if (X == G->childL)
G->childL = N;
else
G->childR = N;
}
else
tree->root = N; // N ist die neue Wurzel des ganzen Baums
break;
// Da ist kein fall thru, nur break; oder continue;
}
// Wird die Schleife nicht durch ein break; beendet,
// dann wird der ganze Baum um 1 höher.
|
Löschen (Austragen, Entfernen)
Die Navigation zum zu löschenden Knoten kann mittels einer Suche, aber auch durch einen Querschritt erfolgen. Beim Löschen (englisch: delete oder remove) sind mehr Fälle zu unterscheiden als beim Einfügen (s. Binärer Suchbaum). Einfach sind die Fälle, wo der zu löschende Knoten ein (Halb-)Blatt ist. Hat er aber zwei Kinder, müssen die beiden frei werdenden Teilbäume neu aufgehängt werden. Dazu wählt man einen der In-order-Nachbarn, also entweder den rechtesten Knoten des linken Kindbaums oder den linkesten des rechten Kindbaums, als Ersatzelter,[10] um die beiden Teilbäume daran wieder aufzuhängen. Der hierfür erforderliche Abstieg geht maximal über so viele Stufen, wie die Höhe beträgt, und im Mittel über genau eine. Der Ersatzknoten wird in der Hierarchie des Baums an der Stelle des gelöschten Knotens eingeklinkt, muss dabei aber selbst aus seinem Herkunftsteilbaum entfernt werden – das ist einfach, da er ein (Halb-)Blatt ist.
Wenn ein Blatt, das ist ein Teilbaum bestehend aus 1 Knoten, entfernt wird, vermindert sich dessen Höhe von 1 auf 0, und wenn ein Blatt an die Stelle eines Halb-Blatts nachrückt, vermindert sich dessen Höhe von 2 auf 1. Alle Höhenänderungen müssen wenigstens in den AVL-Balance-Faktoren reflektiert werden.[Anm 8] Beim Aufstieg zum Elterknoten (und später bei jedem weiteren Aufstieg) gibt es entsprechend der 3 Werte des ursprünglichen Balance-Faktors dieses Knotens 3 Möglichkeiten für den neuen (temporären) Balance-Faktor:
- Wird der Balance-Faktor zu ±1 (er war vorher 0), dann ändert sich die Höhe nicht – mit der Folge, dass die Balance-Faktoren oberhalb bleiben können, wie sie sind, und das AVL-Kriterium für den ganzen Baum erfüllt ist.
- Wird der Balance-Faktor zu 0, verringert sich die Höhe des Teilbaums um 1, und die Überprüfung der Balance-Faktoren oberhalb muss weitergehen.
- Wird der Balance-Faktor zu ±2, muss der Teilbaum rebalanciert werden (siehe Rebalancierung weiter unten). Danach kann bei der Löschoperation der neue Teilbaum eine um 1 niedrigere Höhe als vorher haben – mit der Folge, dass weiterhin überprüft und gegebenenfalls rebalanciert werden muss.
Es kommt aber auch vor, dass sich die gleiche Höhe wie vor dem Löschen ergibt, sodass die Balance-Faktoren oberhalb bleiben können, wie sie sind, und das AVL-Kriterium für den ganzen Baum auch schon erfüllt ist.
Der Aufwand fürs Löschen ist im schlechtesten Fall logarithmisch (mit oder ohne Suchen); im Mittel aber – bspw. wenn das Auffinden des Löschkandidaten nicht mitgerechnet werden muss, weil es anderweitig bewerkstelligt werden kann – ist er konstant, da die Wahrscheinlichkeit für die Notwendigkeit, die Balance auf der nächsthöheren Ebene überprüfen zu müssen, nach oben hin exponentiell abnimmt.[Anm 9]
| Code-Schnipsel |
|
Bei der Löschung eines Knotens N als Kind von X geht der entsprechende Teilbaum von X von Höhe 1 auf 0 oder von Höhe 2 auf 1, wenn N noch ein (inneres) Kind hatte. Schleifeninvariante bei der Löschung Die Höhe des Teilbaums N verringert sich um 1. Er ist in AVL-Form. // Schleife vom Blatt bis möglicherweise zur Wurzel:
for (X = N->parent; X != null; X = G) {
G = X->parent; // Retten X->parent vor Rotation
if (N == X->childL) { // Der linke Teilbaum ist es, der niedriger wird.
if (X->BF <= 0) { // X ist nicht rechtslastig
if (X->BF < 0) { // X ist linkslastig
X->BF = 0;
N = X; // Height(N) wird niedriger um 1
continue;
} // X->BF == 0
X->BF = +1; // N’s Höhenabnahme aufgefangen bei X
break; // Verlassen der Schleife
}
else { // X ist rechtslastig
// ===> X->BF temporär == +2
// ===> Rebalancierung erforderlich
Z = X->childR; // das Geschwister von N (höher um 2)
b = Z->BF;
if (b < 0) // Rechts-Links-Situation (s. Abbildung 3)
N = rotate_RightLeft(X,Z); // Doppelrotation: Right(Z) dann Left(X)
else // Rechts-Rechts-Situation (s. Abbildung 2)
N = rotate_Left(X,Z); // Einfachrotation Left(X)
}
}
else { // (N == X->childR): Der rechte Teilbaum wird niedriger
if (X->BF >= 0) { // X ist nicht linkslastig
if (X->BF > 0) { // X ist rechtslastig
X->BF = 0;
N = X; // Height(N) wird niedriger um 1
continue;
} // X->BF == 0
X->BF = –1; // N’s Höhenabnahme aufgefangen bei X
break; // Verlassen der Schleife
}
else { // X ist linkslastig
// ===> X->BF temporär == –2
// ===> Rebalancierung erforderlich
Z = X->childL; // das Geschwister von N (höher um 2)
b = Z->BF;
if (b > 0) // Links-Rechts-Situation
N = rotate_LeftRight(X,Z); // Doppelrotation: Left(Z) dann Right(X)
else // Links-Links-Situation
N = rotate_Right(X,Z); // Einfachrotation Right(X)
}
}
// Nach der Rotation die Anpassung der Verknüpfung N<->G:
// N ist die neue Wurzel des rebalancierten Teilbaums
N->parent = G;
if (G != null) {
if (X == G->childL)
G->childL = N;
else
G->childR = N;
}
else
tree->root = N; // N ist die neue Wurzel des ganzen Baums
if (b == 0) // der in Abbildung 2 blass gehaltene Fall
break; // Die Höhe ändert sich nicht: Verlassen der Schleife.
// Height(N) wird niedriger um 1 (== alte Height(X)-1)
}
// Wird die Schleife durch (N->parent == null) beendet,
// dann verringert sich die Höhe des ganzen Baums um 1.
|
Rebalancierung
Links(X)
Wenn bei einer Operation ein Höhenunterschied von mehr als 1 zwischen zwei Geschwister-Teilbäumen entsteht, ist beim Elterknoten das AVL-Kriterium verletzt. Eine entsprechende Korrektur heißt „Rebalancierung“. Als Werkzeuge hierfür eignen sich die sogenannten Rotationen.
Für Einfügungen und Löschungen, bei denen die temporäre Höhendifferenz absolut nie über 2 hinausgeht, werden zwei Varianten benötigt: Einfach- und Doppelrotation. Eine Einfachrotation leistet die Rebalancierung, wenn das innere Kind des um 2 höheren Geschwisters (Z in den zwei Abbildungen 2 und 3[11]), das ist das Kind mit einer Kindesrichtung, die der von Z entgegengesetzt ist, (t23 in der Abbildung 2 beziehungsweise Y in der Abbildung 3) nicht höher ist als sein Geschwister, das äußere Kind (t4 in beiden Abbildungen). Dieser Fall wird in der Literatur als Rechts-Rechts- (resp. gespiegelt Links-Links-)Situation bezeichnet, da X rechts- und Z nicht linkslastig ist, das heißt die zwei Balance-Faktoren +2 und +1 (beim Löschen auch 0) sind, kurz: die Balance zweimal hintereinander die gleiche Richtung hat. Der andere Fall, bei dem das innere Kind höher ist, wird von einer Doppelrotation abgedeckt – in der Literatur Rechts-Links- (resp. Links-Rechts-)Situation genannt, da X rechts- und Z linkslastig ist, das heißt die zwei Balance-Faktoren +2 und −1 sind, kurz: die Balance die Richtung wechselt.
Die Schlüssel bewegen sich bei Rotationen nur „vertikal“ (innerhalb der senkrechten Raster). Die In-order-Reihenfolge der Knoten, die ja die Sortierreihenfolge („horizontal“) abbildet, bleibt also vollkommen erhalten.
Eine Rotation umfasst nur eine konstante Anzahl von Verknüpfungsänderungen an einer konstanten Anzahl von Knoten.
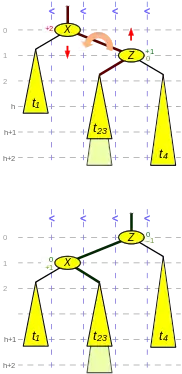
Einfachrotation
Sie wird im Original Малое вращение (kleine Drehung) genannt.
Die obenstehende Abbildung 2 zeigt eine Rechts-Rechts-Situation. In der oberen Hälfte haben die beiden Teilbäume Z und t1 des Knotens X einen Höhenunterschied von +2. Das innere Kind t23 des um 2 höheren Knotens Z ist nicht höher als sein Geschwister t4.
Dies kann nach einem Einfügen in den Teilbaum t4 oder nach einem Löschen aus dem Teilbaum t1 auftreten.
Der in der Abbildung 2 blass gehaltene Fall, dass t23 gleich hoch ist wie t4, kommt nur beim Löschen vor.
Die Rebalancierung (gezeigt in der unteren Hälfte der Abbildung) gelingt durch eine Einfachrotation nach links. Die anzupassenden 3 Verknüpfungen sind in der Abbildung verstärkt gezeichnet, und bei beiden Knoten X und Z ändern sich die Balance-Faktoren.
Die Höhe des neuen Teilbaums Z ist bei einer Einfügung gleich der von X vor der Operation. Dies ist bei einer Löschung genauso, wenn Z nicht rechtslastig war. Bei rechtslastigem Z vermindert sich jedoch die Höhe um 1, und die Überprüfung der Balance-Faktoren oberhalb muss weitergehen.
Die gespiegelte, die Links-Links-Situation wird von einer Einfachrotation nach rechts behandelt.
| Code-Beispiel rotate_Left | ||||||||
node* rotate_Left(node* X,node* Z) {
// Z is um 2 höher als sein Geschwister
t23 = Z->childL; // das innere Kind von Z
X->childR = t23;
if (t23 != null)
t23->parent = X;
Z->childL = X;
X->parent = Z;
// Kommt bei einer Einfügung nicht vor:
if (Z->BF == 0) { // t23 war gleich hoch wie t4
X->BF = +1; // t23 jetzt höher
Z->BF = –1; // t4 jetzt niedriger als X
} else
// Ende: Nicht bei Einfügung
{
X->BF = 0;
Z->BF = 0;
}
return Z; // return neue Wurzel des rebalancierten Teilbaums
}
|
Doppelrotation
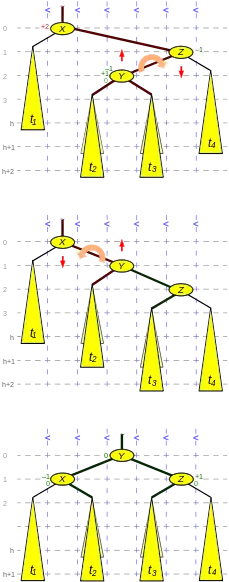
RechtsLinks(X, Z) = Rechts(Z) + Links(X)
Sie wird im Original Большое вращение (große Drehung) genannt.
Die in der Abbildung 3 gezeigte Situation unterscheidet sich von der in Abbildung 2 darin, dass der mittlere Kindbaum (mit Wurzel Y), das ist das innere Kind des um 2 höheren Knotens Z, höher ist als sein Geschwister t4: eine Rechts-Links-Situation, da X rechts- und Z linkslastig ist.
Das kann nach der Einfügung des Knotens Y oder einer Einfügung in einen der Teilbäume t2 oder t3 oder nach einer Löschung aus dem Teilbaum t1 passieren.
Der Fall, bei dem die Teilbäume t2 und t3 gleich hoch sind und der Teilbaum Y höher als t4, kommt nur bei der Löschung vor.
Die Doppelrotation, deren Ergebnis im unteren Drittel der Abb. gezeigt ist, ist eine Rechtsrotation durch Z (gegen die Linkslastigkeit von Z, mittleres Drittel) gefolgt von einer Linksrotation durch X (gegen die Rechtslastigkeit von X). Sie bewirkt eine zweimalige Anhebung des höheren (und inneren) Kindes Y von Z.
Die anzupassenden 5 Verknüpfungen sind in der Abbildung verstärkt gezeichnet, und bei allen 3 Knoten X, Y und Z ändern sich die Balance-Faktoren.[Anm 10]
Die Höhe des neuen Teilbaums Y ist nach einer Einfügung gleich der von X vor der Operation. Bei einer Löschung ist die Höhe jedoch um 1 vermindert, mit der Folge, dass oberhalb die Überprüfung der Balance-Faktoren weitergehen muss.
Bei einer Links-Rechts-Situation wird die gespiegelte Version, das heißt eine Linksrotation gefolgt von einer Rechtsrotation, benötigt.
| Code-Beispiel rotate_RightLeft | ||||||||
node* rotate_RightLeft(node* X,node* Z) {
// Z is um 2 höher als das Geschwister
Y = Z->childL; // das innere Kind von Z
// Y is um 1 höher als das Geschwister
t3 = Y->childR;
Z->childL = t3;
if (t3 != null)
t3->parent = Z;
Y->childR = Z;
Z->parent = Y;
t2 = Y->childL;
X->childR = t2;
if (t2 != null)
t2->parent = X;
Y->childL = X;
X->parent = Y;
// Kommt bei einer Einfügung nicht vor:
if (Y->BF == 0) { // t2 und t3 gleich hoch
X->BF = 0;
Z->BF = 0;
} else
// Ende: Nicht bei Einfügung
if (Y->BF > 0) { // t3 war höher
X->BF = –1; // t1 jetzt höher
Z->BF = 0;
} else
{ // t2 war höher
X->BF = 0;
Z->BF = +1; // t4 jetzt höher
}
Y->BF = 0;
return Y; // return neue Wurzel des rebalancierten Teilbaums
}
|
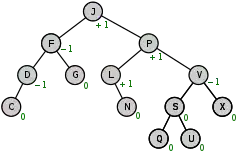
Beispiel
Der AVL-Baum in der Abbildung 1 wird
- nach der Löschung des Knotens »G« durch die zwei Einfachrotationen Rechts(»F«), später Links(»J«)
- nach der Einfügung eines Knotens »T« durch die Doppelrotation LinksRechts(»V«, »S«)
rebalanciert.
Operationen mit ganzen AVL-Bäumen
Die folgenden zwei Operationen haben ganze AVL-Bäume als Ein- und Ausgabeoperanden. Sie gehören nicht zum Standardsatz und fehlen in manchen Implementierungen. Es soll aber hier gezeigt werden, dass auch sie mit logarithmischem Aufwand durchgeführt werden können.
Verketten
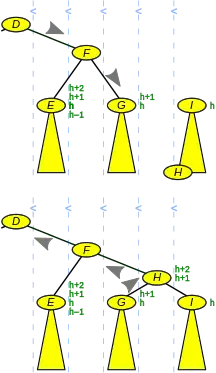
Zwei AVL-Bäume können mit logarithmischem Aufwand verkettet (konkateniert) werden (englisch: concat oder auch nur cat). Für die Sortierfolge müssen natürlich alle Schlüssel des ersten Baums allen Schlüsseln des zweiten vorangehen.[12]
| Algorithmus |
|
Man steigt an der rechten Flanke des ersten Baums (siehe Abbildung 4 – die grauen Pfeile zeigen den Weg durch den Graphen) und an der linken des zweiten bis zu den Blättern hinab und merkt sich die Knoten auf den Pfaden zusammen mit ihren Höhen. Dabei kann die Höhe des Baums um 1 zunehmen. |
Spalten
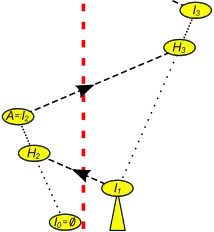
Dick rot gestrichelt: Trennlinie, spezifiziert durch (Knoten, Richtung)
: aufzulösende Kind-Elter-Beziehung zwischen In und Hn+1
: Pfad ohne Überquerung der Trennlinie (von Hn nach In=:A)
: Pfad trifft die Trennlinie zweimal (von In nach Hn+2)
Etwas komplizierter als das Verketten ist das Aufspalten (englisch: split) eines AVL-Baums in zwei separate AVL-Bäume an einem externen Knoten, also einer Stelle zwischen zwei internen Knoten (Schlüsseln), die als Paar (Knoten, Richtung) einschließlich des Pfades zur Wurzel gegeben sei. Links davon liegt die linke Partition mit den kleineren Schlüsseln und rechts davon die rechte mit den größeren. Die so definierte Trennlinie (dick rot gestrichelt in der Abbildung 5) zerschneidet Kanten des Baums auf dem Pfad des Knotens zur Wurzel, so dass sich links wie rechts ein Wald von „Schnipseln“ ergibt.
Jeder der so definierten zwei Wälder kann mit logarithmischem Aufwand zu einem AVL-Baum zusammengefügt werden derart, dass das Ergebnis einer nachfolgenden Verkettung dieser zwei AVL-Bäume in Bezug auf Einträge und deren Reihenfolge zum ursprünglichen Baum äquivalent ist.[12]
| Algorithmus |
|
Die Schnipsel sind Bäume, die bis auf eventuell einen Knoten („Stummel“) (H in den Abbildungen 5 und 6) auf hoher Ebene mit Ausgangsgrad 1 (nicht unbedingt die Wurzel des Schnipsels) in AVL-Form sind. Dieser fungiert beim Verketten mit dem nächstniedrigeren Schnipsel auf der gleichen Seite als Bindeglied. Im Folgenden ist die Indizierung der Knoten so gewählt, dass auf der einen Seite der Trennlinie sich nur geradzahlige, auf der anderen sich nur ungeradzahlige Indizes befinden. Die Indizes wachsen beim Aufstieg in Richtung Wurzel. Vollständige Induktion auszuführen aufsteigend auf beiden Seiten der Trennlinie Induktionsanfang (Abbildung 5): Hat der gegebene (die Trennlinie definierende) Knoten ein Kind in der gegebenen Richtung, dann befindet sich dieses auf der anderen Seite der Trennlinie, ist in AVL-Form und werde I1 genannt. Der gegebene Knoten (nunmehr ein Stummel) werde H2 genannt. H2 ist mit einem Schnipsel I0, welcher in diesem Fall leer ist, zu verketten. Hat der gegebene Knoten kein Kind in der gegebenen Richtung, dann sei H2 sein niedrigster Vorfahr in jener Richtung (also auf der anderen Seite der Trennlinie). I1 sei dessen Kind auf der Seite des gegebenen Knotens – es ist in AVL-Form. H2 ist ein Stummel, der mit einem Schnipsel I0, welcher in diesem Fall leer ist, zu verketten ist. Damit ist I0 (der leere Baum) der niedrigste Schnipsel auf der einen und I1 auf der anderen Seite. Beide sind in AVL-Form. Der Stummel H2 ist ursprünglicher Elter von I1 auf der Gegenseite der Trennlinie und niedrigster Vorfahr von I0 auf der gleichen Seite. 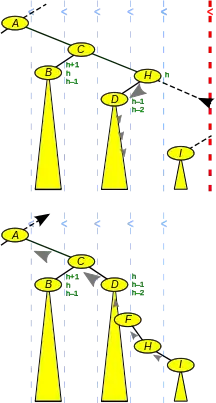 Abb. 6: Ein Induktionsschritt beim Spalten eines AVL-Baums Induktionsschritt (siehe Abbildungen 5 und 6): Beim n-ten Induktionsschritt heißt der niedrigste Schnipsel In. Obwohl die Seite bei jedem Induktionsschritt wechselt, sei der Einfachheit der Erläuterung halber angenommen, dass In wie I in der Abbildung 6 sich links von der Trennlinie befindet. I ist nach Induktionsvoraussetzung ein AVL-Baum. Sein niedrigster Vorfahr auf der linken Seite ist der Stummel H (=:Hn+2). (Dessen rechtes Kind liegt auf der anderen Seite der Trennlinie, ist auch schon in AVL-Form und hat den Namen In+1.) Die ursprüngliche Höhe von H sei h (Abbildung 6 oben). Zerschnittene Elter-Kanten (schwarz gestrichelt mit Pfeil) und die zurückbleibenden Stummel erkennt man am Wechsel der Kindesrichtung beim Aufstieg im Pfad. Dabei sind die (ursprünglichen) Höhen anhand der Balance-Faktoren aufs genaueste mitzuschreiben. Der Teilbaum des Einzelkindes D von H wird mit dem Schnipsel I unter Einsatz von H als Bindeglied verkettet. Bei der Verkettung spielen die Knoten D, F, H und I in der Abbildung 6 dieselbe Rolle wie die Knoten gleichen Namens in der Abbildung 4. Dabei kann Ds Höhe um 1 zunehmen. Falls nun H die Wurzel war, ist der Algorithmus beendet mit D, welches in AVL-Form ist, als der neuen Wurzel des linken Baums. Falls H linkes Kind war, wird D zum neuen niedrigsten Schnipsel auf der linken Seite, erhält den Namen In+2, und der Induktionsschritt n ist beendet. War H rechtes Kind, dann wird D zum dementsprechend rechten Kind bei seinem vormaligen Großelter C gemacht, damit zum Geschwister seines vormaligen Onkels B. Die Höhendifferenz zu letzterem ist maximal 3. Die AVL-Balance von C lässt sich durch Rotationen herstellen, wobei die Höhe von C um 1 abnehmen kann. (Die Vorgehensweise bei einem Höhenunterschied von 3 ähnelt der bei einem von 2: Ist das innere Kind des höheren Geschwisters niedriger als das äußere Kind, kann man die AVL-Balance mit einer Einfachrotation herstellen. Ist es höher, kommt man mit einer Doppelrotation durch. Sind beide Kinder gleich hoch, hängt es vom Balance-Faktor des inneren Kindes ab: ist der höhengleich, macht’s eine Doppelrotation; ist er außenlastig, schaffen’s zwei Rotationen; ist er innenlastig, geht’s mit drei Rotationen.) Man sucht auf der linken Seite aufsteigend nach dem ersten Vorfahr A(=:In+2) im Pfad, der linkes Kind (oder Wurzel) ist. Sein Elter Hn+3 ist niedrigster Vorfahr von In+1 auf der rechten Seite. Links, auf den Ebenen hinauf bis A sind die Balance-Faktoren wie bei einer Löschung zu überprüfen und gegebenenfalls anzupassen, wobei die Höhe um 1 abnehmen kann. Damit ist In so in den Schnipsel A integriert, dass A (oder ein anderer Knoten, der sich bei einer eventuellen Rotation als Wurzel in den Pfad geschoben hat) wieder ein AVL-Baum ist – und den niedrigsten Schnipsel In+2 des Induktionsschrittes n+2 auf dieser linken Seite darstellt. Für den folgenden Induktionsschritt n+3 aber werden die Seiten gewechselt, rechts mit links vertauscht und den Knoten In+1, Hn+3 und In+3 die Rollen von In, Hn+2 und In+2 zugewiesen. Die innerhalb eines Induktionsschrittes besuchten Kanten (graue Pfeile in der Abbildung 6) betreffen nur Ebenen zwischen den Wurzeln von zwei Schnipseln, die auf derselben Seite übereinander liegen (In+2 über In respektive In+3 über In+1). Die Induktionsschritte auf der linken und rechten Seite greifen reißverschlussartig ineinander: der Aufstieg auf der rechten wird auf der linken Seite beim Verketten ab- und wieder aufgestiegen, woran sich ein Aufstieg anschließt, der auf der rechten Seite ab- und wieder aufgestiegen wird usw. Eine Ebene wird höchstens dreimal besucht, jedes Mal mit konstantem Aufwand. Damit ist der Gesamtaufwand fürs Spalten proportional zur Gesamthöhe.[13] |
Anwendungsbeispiele
Die Massenlöschung von allen Schlüsseln in einem zusammenhängenden Bereich (Intervall) kann durch zweimaliges Spalten und einmaliges Verketten geschehen oder, wenn das kleinste oder größte Element mit dabei ist, durch einmaliges Spalten. In ähnlicher Weise lässt sich ein Intervall mit logarithmischem Aufwand als AVL-Baum aus einem AVL-Baum herauspräparieren.
Eine Masseneinfügung kann durch einmaliges Spalten und zweimaliges Verketten durchgeführt werden, sofern die Menge als AVL-Baum vorbereitet ist und ihre Schlüssel in einem Intervall liegen, das im Zielbaum nicht vorkommt.
Implementierung
Zusätzlich zum Bedarf des binären Suchbaums muss in einem Knoten der Balance-Faktor mit seinen 3 Werten untergebracht werden: macht 2 Bits.[Anm 11]
Insbesondere wenn der Prozessor korrekt ausgerichtete Zeiger bevorzugt oder erzwingt, können die Balance-Bits von einem Zeigerfeld im Knoten absorbiert werden, so dass sie kein extra Speicherwort benötigen.
Ansonsten gelten für die Implementierung von AVL-Bäumen dieselben Empfehlungen wie für die binären Suchbäume im Allgemeinen. Auf die Besonderheiten des AVL-Cursors sei im Folgenden explizit eingegangen.
Cursor
Beim Suchen wird ein Paar (Knoten, Richtung) erzeugt, welches geeignet ist, beim Einfügen den Einfügepunkt zu spezifizieren. Beim Löschen wird der zu löschende Knoten durch die Komponente Knoten bezeichnet, und die Komponente Richtung kann zur Angabe verwendet werden, wohin der Cursor nach der Löschung fortschreiten soll. Beim Traversieren gibt Knoten den Ausgangspunkt und Richtung die gewünschte Richtung der Navigation an, um im Ergebnis wieder bei einem solchen Paar anzukommen. Damit erzeugen und/oder verbrauchen alle wichtigen Operationen ein Konstrukt, das (in Analogie zum Beispiel zu den Datenbanken) Cursor genannt wird.[14]
Die Größe des Cursors hängt entscheidend davon ab, ob die AVL-Knoten einen Zeiger zum Elter enthalten oder nicht.
- Elterzeiger vorhanden: Ein Paar (Knoten, Richtung) stellt einen vollwertigen Cursor dar.
Ein Cursor wird nach einer (den Cursor nicht pflegenden) Operation dann und nur dann ungültig, wenn es sich um eine Löschung des Knotens dieses Cursors handelt.
Mit dem prozentualen Aufschlag auf den Speicherbedarf für die Datenstruktur erkauft man sich auf jeden Fall eine prozentuale Einsparung an Laufzeit, da der Rückweg zu Wurzel und Kopf immer schon gesichert ist. - Zeiger zum Elterknoten nicht vorhanden („Cursor mit Stapel“): Zusätzlich zum Paar (Knoten, Richtung) muss der Pfad vom Knoten zu Wurzel und Kopf im Cursor gehalten werden. Die Länge des Cursors entspricht damit der maximalen Höhe des Baums.[Anm 12]
Bei allen Operationen ist der Zugriff zum Elterknoten über den Stapel im Cursor geringfügig teurer als über den Elterzeiger. Soll der Pfad im Cursor auch nach einer modifizierenden Operation gültig gehalten werden (beispielsweise für sequentielle Einfügungen oder Löschungen), kommt noch ein zusätzlicher prozentualer (im Mittel konstanter und im schlechtesten Fall logarithmischer) Aufschlag hinzu. Dies kann so aber nur für einen Cursor, den Eingabecursor, erbracht werden.
In seinem technischen Bericht AVL dags[15][Anm 13] beschreibt G. Myers ein Verfahren, wie mehrere Versionen ein und desselben AVL-Baums in eine Reihenfolge gebracht und in einer Weise miteinander verflochten werden können, die einen logarithmischen Zeit- und Speicherbedarf pro Version nicht überschreitet. Der AVL-Baum ist dann eine so genannte „persistente Datenstruktur“ (englisch persistent data structure).
Trennung der navigierenden von den modifizierenden Operationen
Die Einführung des Cursors erlaubt die Modularisierung der Navigations- von den modifizierenden Operationen. Diese setzt den im Mittel unterlogarithmischen (sprich: konstanten) Aufwand der letzteren frei, denn ein Aufstieg bis zur Wurzel ist (wie in[Anm 7] und[Anm 9] gezeigt) nur in Ausnahmefällen erforderlich. In Anwendungen mit starkem sequentiellem Anteil kann sich das positiv auf die Laufzeit auswirken.
Parallelisierung
Bei iterativer Programmierung kann die Überprüfungs- und Reparaturschleife auch in der umgekehrten Richtung, das heißt „antizipierend“ von Kopf und Wurzel zum Blatt, durchlaufen werden.[16] Das ist insbesondere dann interessant, wenn auf den Baum hochgradig parallel (konkurrent) zugegriffen werden soll. Zum Beispiel würde in einem Szenario „Suchen und Einfügen“ die Suchoperation sich den tiefsten (letzten) höhenungleichen Knoten auf dem Pfad merken, ab dort den Baum sperren[Anm 14] und die Vergleichsergebnisse aufbewahren. Zum Fertigstellen der Einfügeoperation müsste dann der gesperrte Vorfahr (gegebenenfalls nach einer Rebalancierung) auf höhengleich und alle seine Nachfahren bis zum Blatt auf die den eingeschlagenen Richtungen entsprechenden Balance-Faktoren gesetzt werden. Der Vorteil wäre, dass alle Knoten außerhalb des gesperrten Teilbaums von den anderen Prozessorkernen parallel zur laufenden Einfügung konsistent besichtigt und auch verändert werden könnten.
Vergleich mit Rot-Schwarz-Baum
Die Menge der AVL-Bäume ist eine echte Teilmenge in der Menge der Rot-Schwarz-Bäume. Denn jeder Binärbaum, der das AVL-Kriterium erfüllt, lässt sich in einer das Rot-Schwarz-Kriterium erfüllenden Weise einfärben.[17]
| Beweis |
 4 kleine AVL-Bäume in Rot-Schwarz-Färbung. Bei den geteilten Knoten gehen beide Farben. Behauptung: Hat der AVL-Baum eine gerade Höhe , dann lässt er sich mit Schwarztiefe bei schwarzer Wurzel einfärben; ist ungerade, dann mit Schwarztiefe bei einer roten oder mit Schwarztiefe bei einer schwarzen Wurzel. (Die NIL-Knoten sind dabei nicht mitgezählt.) Beweis: Die Behauptung ist richtig für (siehe Abbildung). |

Es gibt aber Rot-Schwarz-Bäume, die das AVL-Kriterium nicht erfüllen. Die nebenstehende Abb. zeigt zum Beispiel einen Rot-Schwarz-Baum mit 6 (inneren) Knoten und der externen Pfadlängensumme 21, während 20 die größte externe Pfadlängensumme bei AVL-Bäumen (und zugleich die kleinstmögliche für alle Binärbäume) dieser Größe ist. Konsequenterweise ist auch die Worst-Case-Höhe des AVL-Baums kleiner als die des Rot-Schwarz-Baums, und zwar um den Faktor mit obigem und dem Faktor 2 aus dem Höhenbeweis des Rot-Schwarz-Baums. Allgemein werden AVL-Bäume als besser balanciert und ihr Suchzeitverhalten als günstiger angesehen.
Der Speicherplatzbedarf ist praktisch identisch: 1 Bit für die Farbe gegenüber 2 oder auch 1 Bit(s)[Anm 11] für den Balance-Faktor.
Der Platzbedarf und das Laufzeitverhalten für die angeführten Operationen ist im Mittel und im Worst Case identisch. Das gilt auch für die amortisiert konstanten Modifikationskosten beim Einfügen.[9] Zwar bietet der Rot-Schwarz-Baum amortisiert konstante Modifikationskosten auch beim Löschen[18] und der AVL-Baum dort nur[Anm 15] im Mittel konstante. Anwendungen von binären Suchbäumen, die nur Sequenzen von Einfügungen und Löschungen – ganz ohne intervenierende Suchoperationen – enthalten, gehen am Zweck des Suchbaums vorbei. Sieht man also von dieser Art Anwendungen ab, ist das Gesamtverhalten einer Mischung von Suchen und Modifikation bei beiden Datenstrukturen amortisiert, im Mittel und im Worst Case logarithmisch.
Realistische Anwendungssituationen mit Performancedaten und -vergleichen – auch mit weiteren Suchalgorithmen und Spielarten der Datenstrukturen – finden sich bei Ben Pfaff.[19] Seine Ergebnisse zeigen in 79 Messungen unter anderem die sehr große Ähnlichkeit von AVL-Bäumen (AVL) und Rot-Schwarz-Bäumen (RB) mit Laufzeitverhältnissen AVL⁄RB zwischen 0,677 und 1,077 bei einem Median von ≈0,947 und einem geometrischen Mittelwert von ≈0,910.
Anwendungen
Als grundlegende Hilfsmittel der Informatik haben die binären Suchbäume ein großes Einsatzgebiet, in welchem sie aber auch hochgradig untereinander austauschbar sind. Konkrete Beispiele und Auswahlkriterien finden sich in Binärer Suchbaum#Anwendungen.
Siehe auch
Literatur
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein: Introduction to Algorithms. 2. Auflage. MIT Press, Cambridge MA 2001, ISBN 0-262-03293-7.
- Ralf Hartmut Güting, Stefan Dieker: Datenstrukturen und Algorithmen. Stuttgart 2004, ISBN 978-3-519-22121-0.
- Donald E. Knuth: The Art of Computer Programming. 2. Auflage. Band 3: Sorting and Searching. Addison-Wesley, 1998, ISBN 0-201-89685-0, 6.2.3 Balanced Trees, S. 458–478.
- Udi Manber: Introduction to Algorithms – A Creative Approach. Addison-Wesley Publishing Company 1989, Kapitel 4.3.4, S. 75ff.
- Kurt Mehlhorn: Datenstrukturen und effiziente Algorithmen. Teubner Stuttgart 1988, ISBN 3-519-12255-3.
- Kurt Mehlhorn, Peter Sanders: Algorithms and Data Structures. The Basic Toolbox. Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-77977-3, doi:10.1007/978-3-540-77978-0.
Weblinks
- Paul E. Black: AVL tree. In: Dictionary of Algorithms and Data Structures. National Institute of Standards and Technology (NIST), 7. Juli 2014, abgerufen am 27. Juli 2016 (englisch).
- Algorithmenvisualisierung unter anderem für AVL-Bäume
- Kurz gehaltene Beschreibung der Rotationen
- AvlTree.cs vom 10. August 2012
- Ben Pfaff: An Introduction to Binary Search Trees and Balanced Trees. Free Software Foundation, Boston 2004, gnu.org (PDF gzip; 1675 kB).
- Ben Pfaff: Performance Analysis of BSTs in System Software. Stanford University, 2004, stanford.edu (PDF; 316 kB).
Einzelnachweise
- Thomas H. Cormen u. a.: Introduction to Algorithms. 2. Auflage, MIT Press, Cambridge (Massachusetts) 2001, S. 296.
- G. M. Adelson-Velsky, E. M. Landis: Один алгоритм организации информации. In: Doklady Akademii Nauk SSSR. 146, 1962, S. 263–266. (russisch)
Englische Übersetzung von Myron J. Ricci: An algorithm for the organization of information. (Memento vom 1. Februar 2014 im Internet Archive) (PDF) In: Soviet Mathematics 3, 1962, S. 1259–1263. - In der englischen Literatur meist „balance factor“, so bei Donald E. Knuth: The Art of Computer Programming. Band 3, Sorting and Searching, 2. Auflage, Addison-Wesley, 1998, S. 459; „Höhenbalance“ bei Kurt Mehlhorn: Datenstrukturen und effiziente Algorithmen. Teubner, Stuttgart 1988, S. 295.
- Donald E. Knuth: The Art of Computer Programming. Band 3, Sorting and Searching, 2. Auflage, Addison-Wesley, 1998, S. 460.
- Ben Pfaff Performance Analysis of BSTs in System Software S. 2
- s. Donald Knuth: The Art of Computer Programming S. 460.
- Diesen Weg geht Donald Knuth in The Art of Computer Programming S. 462.
- so Ben Pfaff in An Introduction to Binary Search Trees and Balanced Trees § 34.
- Dinesh P. Mehta, Sartaj Sahni (Hrsg.) Handbook of Data Structures and Applications 10.4.2
- Laut Robert Sedgewick, Kevin Wayne: Algorithms Fourth Edition. (PDF) (Seite nicht mehr abrufbar, Suche in Webarchiven) Info: Der Link wurde automatisch als defekt markiert. Bitte prüfe den Link gemäß Anleitung und entferne dann diesen Hinweis. (PDF) Pearson Education, 2011, ISBN 978-0-321-57351-3, S. 410 (englisch, abgerufen am 25. März 2018) stammt der Vorschlag aus dem Jahr 1962 von T. Hibbard. In An Introduction to Binary Search Trees and Balanced Trees S. 39 wählt Ben Pfaff – so vorhanden – stets den letzteren. Man kann aber auch den ersteren nehmen oder von beiden Teilbäumen den eventuell höheren.
- Die Abbildungen entsprechen Donald Knuth The Art of Computer Programming S. 461 Case1 (Einfachrotation) und Case2 (Doppelrotation).
- Donald E. Knuth: The Art of Computer Programming, Band 3, Sorting and Searching, 2. Auflage, Addison-Wesley, 1998, S. 474
- Costin S, der in seinem Projekt AvlTree.cs AVL-Bäume mit Concat- und Split-Operationen implementiert, fordert dazu die Aufzeichnung der vollen absoluten Höhe in jedem Knoten. Man kann aber – wie gezeigt – mit den Balance-Faktoren auskommen, ohne den Aufwand zu erhöhen.
- Ben Pfaff gibt einem Objekt mit sehr ähnlicher Funktionalität den Namen „traverser“ und offeriert für Suchen, Einfügen und Löschen eine Standard- und eine Traverser-Variante. (An Introduction to Binary Search Trees and Balanced Trees S. 15 und Performance Analysis of BSTs in System Software S. 3)
- Eugene W. Myers: AVL dags. In: Technical Report, Department of Computer Science, U. of Arizona. 82-9, 1982. Zitiert nach: Neil Sarnak, Robert E. Tarjan: Planar Point Location Using Persistent Search Trees Archiviert vom Original am 10. Oktober 2015. In: Communications of the ACM. 29, Nr. 7, 1986, S. 669–679. doi:10.1145/6138.6151. Abgerufen am 25. Dezember 2014.
- „Top-Down-Strategie“ bei Kurt Mehlhorn: Datenstrukturen und effiziente Algorithmen. Teubner, Stuttgart 1988, S. 197–198.
- Paul E. Black: AVL tree. In: Dictionary of Algorithms and Data Structures. National Institute of Standards and Technology, 13. April 2015, abgerufen am 2. Juli 2016 (englisch).
- Kurt Mehlhorn, Peter Sanders: Algorithms and Data Structures. The Basic Toolbox. Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-77977-3, doi:10.1007/978-3-540-77978-0. S. 165.
- Ben Pfaff: Performance Analysis of BSTs in System Software. Stanford University 2004.
Anmerkungen
- Da einem Knoten in umkehrbar eindeutiger Weise der von ihm gewurzelte maximale Unterbaum, „sein“ Teilbaum, zugeordnet werden kann, sollen der Kürze halber Eigenschaften wie Höhe, Balance, Elter-Kind- und Geschwister-Beziehung usw. einem Knoten und einem solchen Teilbaum in gleicher Weise zukommen.
Spielt dabei die Beziehung zum Elter eine Rolle, so sei noch spezifischer vom linken (oder rechten) Kindbaum die Rede.
Umgekehrt fungiert, zum Beispiel beim Umhängen eines Teilbaums, dessen Wurzel als „Henkel“. - Im Prinzip kann man auch die gespiegelte Differenz nehmen. Der Text folgt Knuth und vielen weiteren Autoren.
- Die Rekursionsgleichung für die Höhe ist
- Aus den Balance-Faktoren (≤ 2 Bits pro Knoten) lassen sich alle relevanten Daten für Einfügen und Löschen berechnen, es bedarf nicht der Kenntnis der absoluten Höhen.
- gemäß der Definition Binärer Suchbaum#Abb1A, bei der die Knotenebenen gezählt werden und der nur aus der Wurzel bestehende Baum die Höhe 1 hat
- Strebt beim Fibonacci-Baum die Anzahl der Knoten gegen unendlich, dann verhält sich seine mittlere Suchtiefe asymptotisch wie
- mit ,
-
Sei die Anzahl der Knoten, die nicht Blätter sind und die zwei Kindbäume gleicher Höhe haben, und die Anzahl der Knoten mit verschieden hohen Kindbäumen, dann ist der Anteil der höhenungleichen.
(Nur die Fibonacci-Bäume und die anderen dünnsten AVL-Bäume erreichen exakt . Dagegen kommen nur die vollständigen Binärbäume (mit inneren Knoten) auf exakt .
Der Mittelwert über alle möglichen Formen von AVL-Bäumen liegt bei .)
Von folgender Situation sei rekursiv ausgegangen: Bei einer Einfügung habe sich ergeben, dass die Höhe des Teilbaums, in dem die Einfügung stattfand, um 1 zugenommen hat. Ferner sei angenommen, dass es sich um einen rechten Kindbaum handelt (dazu passen die Abbildungen 2 und 3; die gespiegelte Alternative linker Kindbaum sei dem Leser überlassen, sie führt zu denselben Werten). Bei der Überprüfung der Lage im Elterknoten dieses Teilbaums sind die folgenden Fälle zu unterscheiden:
Die Wahrscheinlichkeit, bei einer Einfügung ausgehend von einer Ebene die nächsthöhere überprüfen zu müssen, ist also . Unter der Annahme, dass diese Wahrscheinlichkeiten für alle Ebenen gleich sind, ist die Wahrscheinlichkeit, dass wenigstens Ebenen überprüft werden müssen, gleich und, dass genau Ebenen überprüft werden müssen, gleich . Somit summiert sich die Anzahl der zu überprüfenden Ebenen im Mittel aufBF
vor
EinfügungHäufigkeit vorläu-
figer
BFRebalan-
cierung
erforderlichBF
da-
nachTeilbaum
wird
höher umEbene ober-
halb zu
überprüfen−1 links höher 0 Nein 0 Nein 0 höhengleich +1 Nein 1 Ja +1 rechts höher +2 Ja 0 0 Nein Tab. 2: Nach dem Einfügen: Die neuen Balance-Faktoren (BF) in Abhängigkeit von den alten - Wie beim Einfügen kann der Baum auch beim Löschen von oben nach unten („top-down“) repariert werden. Der Einfachheit halber sei hier nur die Reparatur von unten nach oben („bottom-up“) erläutert. So spielt sie sich auch bei rekursiver Programmierung ab.
- Über den Anteil der höhenungleichen Knoten seien dieselben Annahmen wie bei der Einfügung gemacht.
Folgende Situation sei rekursiv angenommen: Nach einer Löschung habe sich die Höhe des Teilbaums, in dem die Löschung stattfand, um 1 vermindert. Ferner handele es sich ohne Beschränkung der Allgemeinheit um einen linken Kindbaum. Bei der Überprüfung der Lage im Elterknoten dieses Teilbaums sind die folgenden Fälle zu unterscheiden:
Bei einer Löschung ergibt sich eine Wahrscheinlichkeit für das Erfordernis, die nächsthöhere Ebene überprüfen zu müssen. Unter der Annahme, dass diese Wahrscheinlichkeiten für alle Ebenen gleich sind, summiert sich die mittlere Anzahl der zu überprüfenden Ebenen aufBF
vor
LöschungHäufigkeit vorläu-
figer
BFRebalan-
cierung
erforderlichBF
da-
nachTeilbaum
wird nied-
riger umEbene ober-
halb zu
überprüfen−1 links höher 0 Nein 1 Ja 0 höhengleich +1 Nein 0 Nein +1 rechts höher +2 Ja +1 0 1 Nein 0 1 2 Ja 1 Die vorletzte Zeile bezieht sich auf den Fall der Einfachrotation mit gleich hohen Kindern und2 die letzte auf Rotationen mit nicht gleich hohen Kindern des höheren Knotens Z (s. Abb. 2 und 3), d. h.
Doppelrotation (linkes Kind Y höher) resp. Einfachrotation mit dem rechten Kind t4 höher.Tab. 3: Nach dem Löschen: Die neuen Balance-Faktoren (BF) in Abhängigkeit von den alten - .
- Man beachte, dass im Fall eines rechtslastigen Y die erste Teilrotation einer Doppelrotation die Situation im betroffenen Teilbaum Y sogar verschlechtert; erst die zweite mit einer Rotationsachse außerhalb bringt die Sache in Ordnung. Somit entspricht, was die Balance-Faktoren angeht, weder die erste noch die zweite Teilrotation einer AVL-#Einfachrotation.
- 1 Bit, wenn bei den Kindern aufgezeichnet. Wird dem Bit die Bedeutung „Höhensprung oberhalb“ gegeben, dann kann die Höhe im Pfad ohne Kenntnis der Kindesrichtung berechnet werden. Dennoch: es ist für die Modifikationsoperationen geschickter, die 2 Balance-Bits in einem Byte nebeneinander zu haben.
- Als eine Datenstruktur, die im homogenen Arbeitsspeicher (Hauptspeicher) untergebracht ist, ist der AVL-Baum durch dessen Größe beschränkt, also auch die Höhe des Baums und die Längen der Pfade von Blatt zu Wurzel. Gängig sind Hauptspeicher mit 32 Bit und 64 Bit breiten 8-Bit-Byte-Adressen.
Fazit: Es ist bei AVL-Bäumen vertretbar, Cursor mit Stapeln bereitzustellen, die so groß sind, dass ein Überlauf nicht auftreten kann.Breite
eines
Zeigers
in Bitmaximale Anzahl adressierbarer Bytes minimale Knotenlänge
(2 Zeiger+1 Byte
+Nutzdaten 1)maxi-
male Anzahl KnotenKnotenzahl des nächstgrößeren Fibonacci-Baums … … der Höhe 32 4294967296 2·4+1+3 = 12 3,6·108 433494436 41 64 18446744073709551616 2·8+1+7 = 24 7,7·1018 1100087778366101930 86 1 inklusive Schlüssel. Bei mehr Nutzdaten und weniger Hauptspeicher
verringert sich die maximale Knotenzahl und Höhe entsprechend.Tab. 4: Maximale Höhe in Abhängigkeit von der Adressierungsbreite - dag für „Directed Acyclic Graph“, deutsch: Gerichteter azyklischer Graph
- Genau genommen bedarf es einer Kette mit den Gliedern Sperren(Kind) und Entsperren(Elter) bis zum ersten höhenungleichen Knoten, der zunächst gesperrt bleibt, bis er in ein neues Wechselspiel mit den Gliedern Sperren(höhenungleichen Knoten) und Entsperren(Vorfahr) eintritt. (Dabei bedeutet Sperren(Knoten) eigentlich Sperren(Teilbaum). Und: bei einer potentiellen Rebalancierung muss die Sperre sogar eine Ebene höher gehalten werden.) Ist der Einfügepunkt erreicht, kann auch schon mit der Korrektur- und Entsprerrschleife begonnen werden – für maximale Parallelität wieder in einer Kind-Elter-Kette.
Wenn alle nebenläufigen Mitspieler diese Gerichtetheit des Sperrprotokolls einhalten, kann eine zirkuläre Abhängigkeit und damit eine Verklemmung (deadlock) nicht entstehen. - Bei einem vollständigen Binärbaum bedingt eine -fache Schleife bestehend aus Einfügung eines zusätzlichen Knotens und Löschung desselben jedesmal die Anpassung von Balance-Faktoren bis hinauf zur Wurzel und damit einen Aufwand in , also amortisiert .