Binärbaum
Binärbäume sind in der Informatik die am häufigsten verwendete Unterart der Bäume. Im Gegensatz zu anderen Arten von Bäumen können die Knoten eines Binärbaumes nur höchstens zwei direkte Nachkommen haben.
Meist wird verlangt, dass sich die Kindknoten eindeutig in linkes und rechtes Kind einteilen lassen. Ein anschauliches Beispiel für einen solchen Binärbaum ist die Ahnentafel, bei der allerdings die Elternteile durch die Kindknoten zu modellieren sind.
Ein Binärbaum ist entweder leer, oder er besteht aus einer Wurzel mit einem linken und rechten Teilbaum, die wiederum Binärbäume sind. Ist ein Teilbaum leer, bezeichnet man den entsprechenden Kindknoten als fehlend.
Meistens wird die Wurzel in graphischen Darstellungen (wie in der nebenstehenden) oben und die Blätter unten platziert. Entsprechend ist ein Weg von der Wurzel in Richtung Blatt einer von oben nach unten.
Begriffe
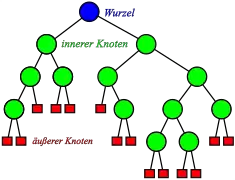
zu finden bei Rot-Schwarz-Bäumen
Die Begriffe Knoten und Kante werden von den Graphen übernommen. Die Kante ist definitionsgemäß gerichtet (auch: Bogen oder Pfeil). Wenn es aus dem Kontext klar genug hervorgeht, wird auch nur von Kante gesprochen.
Bei gerichteten Graphen kann man einem Knoten sowohl Ausgangsgrad wie Eingangsgrad zuordnen. Üblicherweise werden Binärbäume als Out-Trees aufgefasst. In einem solchen gewurzelten Baum gibt es genau einen Knoten, der den Eingangsgrad 0 hat. Er wird als die Wurzel bezeichnet. Alle anderen Knoten haben den Eingangsgrad 1. Der Ausgangsgrad ist die Anzahl der Kindknoten und ist beim Binärbaum auf maximal zwei beschränkt. Damit ist seine Ordnung als Out-Tree ≤ 2. Knoten mit Ausgangsgrad ≥ 1 bezeichnet man als innere Knoten, solche mit Ausgangsgrad 0 als Blätter oder äußere Knoten.
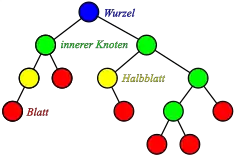
Vielfach findet sich in der Literatur auch eine Sichtweise, bei der alle Knoten Information tragen und externe Blätter nicht vorkommen. Dann gibt es bei Binärbäumen – und nur dort – gelegentlich die Bezeichnung Halbblatt für einen Knoten mit Ausgangsgrad 1 (englisch manchmal: non-branching node).
Die Höhe eines gewurzelten Baums ist die maximal auftretende Tiefe. Viele Autoren setzen sie aber um eins höher, da man so dem leeren Baum die Höhe 0 und dem nur aus der Wurzel bestehenden Baum die Höhe 1 geben kann, was gewisse rekursive Definitionen kürzer zu fassen gestattet. (Und da Tiefe ein Attribut eines Knotens, Höhe aber eines des ganzen Baums ist, muss es nicht unbedingt Verwirrungen geben.)[1]
- Zur Beachtung
In diesem Artikel ist die letztere Sichtweise durchgehalten:
- Alle Knoten einschließlich Wurzel und Blätter tragen Information („knotenorientierte Speicherung“).
- Die Höhe des Baums ist die Maximalzahl der Knotenebenen.
Ein Binärbaum heißt geordnet, wenn jeder innere Knoten ein linkes und eventuell zusätzlich ein rechtes Kind besitzt (und nicht etwa nur ein rechtes Kind), sowie der linke Knoten „kleiner“, der rechte Knoten „größer“ als der Betrachtungsknoten ist. Man bezeichnet ihn als voll, wenn jeder Knoten entweder Blatt ist (also kein Kind besitzt), oder aber zwei (also sowohl ein linkes wie ein rechtes) Kinder besitzt – es also kein Halbblatt gibt. Für die Eigenschaft voll werden gelegentlich auch die Begriffe saturiert oder strikt verwendet. Man bezeichnet volle Binärbäume als vollständig, wenn alle Blätter die gleiche Tiefe haben, wobei die Tiefe eines Knotens als die Anzahl der Bögen bis zur Wurzel definiert ist.
Der Binärbaum wird entartet genannt, wenn jeder Knoten entweder Blatt ist (Anzahl Kinder ist 0) oder Halbblatt (Anzahl Kinder ist 1). In diesem Fall stellt der Baum eine Liste dar. Besondere Formen sind die geordneten Listen, bei denen ein Baum jeweils nur aus linken oder nur aus rechten Kindern besteht.
Eigenschaften
- So wie ein Baum mit Knoten Kanten hat, hat ein Binärbaum mit Knoten Kanten.
- Ein Binärbaum mit Knoten hat (unmittelbare) Einfügepunkte.
- Ein Binärbaum mit Blättern und Halbblättern hat an jedem Halbblatt einen Einfügepunkt und an jedem Blatt zwei, also (unmittelbare) Einfügepunkte.
- Ist die Anzahl der inneren Knoten, so errechnet sich .
Kombinatorik
Die Anzahl der Binärbäume mit Knoten entspricht der Anzahl der Möglichkeiten, eine Zeichenfolge von geordneten Symbolen, die durch mathematische Operatoren für eine zweistellige Verknüpfung, zum Beispiel Addition, Subtraktion, Multiplikation oder Division, getrennt sind, vollständig in Klammern zu setzen. Die Reihenfolge der Zahlen oder Elemente, zum Beispiel Matrizen, ist festgelegt. Die Operation muss weder assoziativ noch kommutativ sein.
Dabei entspricht jeder Knoten einer zweistelligen Verknüpfung und für jeden Knoten entspricht der linke Teilbaum dem linken Ausdruck und der rechte Teilbaum dem rechten Ausdruck der Verknüpfung.
Zum Beispiel muss man für eine Zeichenfolge wie in Klammern setzen, was auf fünf verschiedene Arten möglich ist:
Ein explizites Beispiel für die Subtraktion ist
Das Hinzufügen redundanter Klammern um einen bereits in Klammern gesetzten Ausdruck oder um den vollständigen Ausdruck herum ist nicht zulässig.
Es gibt einen Binärbaum mit 0 Knoten und jeder andere Binärbaum ist durch die Kombination aus seinem linken und seinem rechten Teilbaum gekennzeichnet. Wenn diese Teilbäume bzw. Knoten haben, hat der gesamte Baum die Knoten. Daher hat die Anzahl von Binärbäumen mit Knoten die folgende rekursive Beschreibung und für jede positive ganze Zahl . Daraus folgt, dass die Catalan-Zahl mit Index ist. Es gilt
| Anzahl der Binärbäume | |
|---|---|
| n | Cn |
| 1 | 1 |
| 2 | 2 |
| 3 | 5 |
| 4 | 14 |
| 5 | 42 |
| 6 | 132 |
| 7 | 429 |
| 8 | 1430 |
Anwendungen
Binärer Suchbaum
Die in der Praxis wohl wichtigste Anwendung der Binärbäume sind die binären Suchbäume, worunter die AVL-Bäume, Rot-Schwarz-Bäume und Splay-Bäume zu rechnen sind. Bei Suchbäumen gibt es in jedem Knoten „Schlüssel“, nach denen die Knoten „linear“ im Baum geordnet sind. Auf dieser Ordnung basiert dann ein möglichst effizientes Suchen.
Partiell geordneter Baum
Ein partiell geordneter Baum T ist ein spezieller Baum,
- dessen Knoten markiert sind
- dessen Markierungen aus einem geordneten Wertebereich stammen
- in dem für jeden Teilbaum U mit der Wurzel x gilt: Alle Knoten aus U sind größer markiert als x oder gleich x.
Intuitiv bedeutet dies: Die Wurzel jedes Teilbaumes stellt ein Minimum für diesen Teilbaum dar. Die Werte des Teilbaumes nehmen in Richtung der Blätter zu oder bleiben gleich.
Derartige Bäume werden häufig in Heaps verwendet.
Vollständiger Binärbaum und vollständig balancierter Binärbaum
Ein vollständiger Binärbaum ist ein voller Binärbaum (alle Knoten haben entweder 2 oder 0 Kinder), in dem alle Blätter die gleiche Tiefe haben. Induktiv lässt sich zeigen, dass ein vollständiger Binärbaum der Höhe , den man häufig als bezeichnet, genau
- Knoten,
- innere Knoten (nicht Blatt, aber evtl. Wurzel),
- Knoten in Tiefe für , insbesondere also
- Blätter
besitzt.
Ein vollständig balancierter Binärbaum ist ein voller Binärbaum, bei dem die Abstände von der Wurzel zu zwei beliebigen Blättern um höchstens 1 voneinander abweichen. Ein vollständiger Binärbaum ist ein vollständig balancierter Binärbaum. (Vergleiche Balancierter Baum und AVL-Baum.)
Weitere Binärbäume
Eine Darstellung eines Binärbaumes, in dem die Knoten mit rechtwinkligen Dreiecken und die Bögen mit Rechtecken dargestellt werden, nennt man pythagoreischen Binärbaum.
Auch Fibonacci-Bäume und binäre Heaps basieren auf Binärbäumen.
Repräsentation und Zugriff
Die Abbildung zeigt eine naheliegende Art der Speicherung. Sie entspricht in etwa den C-Strukturen:
struct knoten { // 1 Objekt = 1 Knoten
char schlüssel;
struct knoten * links; // linkes Kind
struct knoten * rechts; // rechtes Kind
} object;
struct knoten * anker; // Zeiger auf die Wurzel
Zur besseren Unterscheidung der Objekte sind diese beziehentlich mit den Schlüsseln »F«, »G«, »J« und »P« versehen. Diese Schlüssel sind auch der Einfachheit halber als Ziel der Verweise genommen worden (anstelle von echten Speicheradressen). Wie üblich soll ein Zeigerwert 0 ausdrücken, dass auf kein Objekt verwiesen wird, es also kein Kind an dieser Stelle gibt.
Der große Vorteil des Baums gegenüber dem Array liegt in der flexibleren Speicherverwaltung: Mit dem Entstehen oder Vergehen eines Objektes kann auch der es darstellende Speicher entstehen oder vergehen, wogegen die einzelnen Einträge beim Array fest mit diesem verbunden sind.
In-Order-Index
Wird in jedem Knoten die Anzahl der Elemente des zugehörigen Unterbaums gehalten, kann das Aufsuchen eines Elements vermöge seines in-order-Index in ganz ähnlicher Weise wie das Aufsuchen mit einem Schlüssel im binären Suchbaum bewerkstelligt werden. Dies hat allerdings die nachteilige Implikation, dass Einfüge- und Löschoperation immer Korrekturen bis hinauf zur Wurzel erfordern, womit sich dann auch die in-order-Indizes von Knoten ändern. Die Vorgehensweise dürfte also bei nicht statischen Binärbäumen von fraglichem Wert sein, und bei statischen ist der gewöhnliche Array-Index in Bezug auf Laufzeit überlegen.
Der Aufwand ist , wobei die Höhe des Baums ist.
Links/Rechts-Index
Jeder Knoten kann durch eine variabel lange Kette von Binärziffern genau spezifiziert werden. Die Maßgabe könnte folgendermaßen lauten:
- Eine „0“ am Anfang (gleichzeitig Ende) entspricht dem leeren Binärbaum.
- Eine „1“ am Anfang lässt auf die Wurzel zugreifen.
- Eine anschließende „0“ bzw. „1“ lässt auf das linke bzw. rechte Kind zugreifen.
Jedem Knoten in einem Binärbaum kann so eindeutig eine Binärkette zugeordnet werden.
Bei höhen-balancierten Bäumen ist die Binärkette in ihrer Länge durch beschränkt, so dass sie in ein vorzeichenloses Integer passen mag. Eine denkbare Codierung der variablen Länge in einem Wort fester Länge lässt die Binärkette nach der ersten „1“ beginnen.
Der maximale Aufwand für einen Zugriff ist .
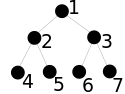
Repräsentation durch ein Array
Ein Binärbaum kann durch ein Array repräsentiert werden, dessen Länge im Wesentlichen der Anzahl der Knoten des Baumes entspricht, genauer: mit als der Höhe des Baumes. Eine Anordnung findet sich bei der binären Suche im Array.
Eine andere Art der Repräsentation beginnt mit der Indizierung bei 1 mit Verweis auf die Wurzel. Dann setzt sie sich „zeilenweise“ fort: alle Knoten derselben Tiefe werden von links nach rechts fortlaufend nummeriert. Das heißt: das Auslesen des Arrays von links entspricht einem Level-Order-Traversal (oder Breadth-First-Traversal) des Baums. Falls der Binärbaum nicht voll besetzt ist, müssen ausgelassene Knoten durch Platzhalter besetzt werden, so dass also Speicherzellen verschwendet werden.
Diese Nummerierung hat die angenehme Eigenschaft, dass man leicht die Indizes der verbundenen Knoten berechnen kann. Im Array sei ein Knoten, dann ist sein linkes und sein rechtes Kind; die abgerundete Hälfte verweist auf den Elter .
In der Genealogie ist dieses Indizierungsschema auch unter dem Begriff Kekule-Nummerierung bekannt.
Da bei der Abbildung von einem Binären Baum in ein Array keine expliziten Zeiger auf Kinder bzw. Elter-Knoten notwendig sind, wird diese Datenstruktur auch als implizite Datenstruktur bezeichnet.
Eine Anwendung dieser Darstellung ist der binäre Heap, der für die Sortierung von Elementen verwendet wird.
Traversierung
Traversierung bezeichnet das systematische Untersuchen der Knoten des Baumes in einer bestimmten Reihenfolge. Von den verschiedenen Möglichkeiten, die Knoten von Binärbäumen zu durchlaufen, unterscheidet man vor allem die folgenden Varianten:[2]
Tiefensuche
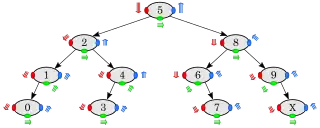
Volle Abfolge der Schlüssel 5–2–1–0–0–0–1–1–2–4–3–3–3–4–4–2–5–8–6–6–7–7–7–6–8–9–9–X–X–X–9–8–5.
Pre-order (NLR, N in roter Position):
5–2–1–0–4–3–8–6–7–9–X;
In-order (LNR, N in grüner Position):
0–1–2–3–4–5–6–7–8–9–X;
Post-order (LRN, N in blauer Position):
0–1–3–4–2–7–6–X–9–8–5.
Bei der Tiefensuche wird ein Pfad zunächst vollständig in die Tiefe (»depth-first«) abgearbeitet, bevor aufsteigend die Seitenzweige bearbeitet werden. Die Umlaufrichtung um den Baum ist standardmäßig entgegen dem Uhrzeigersinn, d. h. der linke Teilbaum L wird vor dem rechten R (jeweils rekursiv) durchlaufen; die umgekehrte Umlaufrichtung wird als »reverse« bezeichnet. Abhängig davon, an welcher Stelle vor, zwischen oder nach L,R der aktuelle Knoten N betrachtet wird, unterscheidet man folgende Fälle:
- pre-order oder Hauptreihenfolge (N–L–R):
Zuerst wird der Knoten N betrachtet und anschließend der linke L, schließlich der rechte Teilbaum R rekursiv durchlaufen. - post-order oder Nebenreihenfolge (L-R–N):
Zuerst wird der linke L, dann der rechte Teilbaum R rekursiv durchlaufen und schließlich der Knoten N betrachtet. - in-order oder symmetrische Reihenfolge (L–N–R):
Zuerst wird der linke Teilbaum L rekursiv durchlaufen, dann der Knoten N betrachtet und schließlich der rechte Teilbaum R rekursiv durchlaufen. Diese Reihenfolge entspricht bei binären Suchbäumen der Anordnung der Schlüssel und ist für die meisten Anwendungen die gegebene. - reverse in-order oder anti-symmetrische Reihenfolge (R–N–L):
Zuerst wird der rechte Teilbaum R durchlaufen, dann der Knoten N betrachtet und schließlich der linke Teilbaum L durchlaufen.
Rekursive Implementierungen
Die Aktion, die an einem Knoten auszuführen ist, geschieht im Unterprogramm callback, das vom Benutzer zu liefern ist. Eine gewisse Kommunikation mit dem aufrufenden Programm kann bei Bedarf über die Variable param vorgenommen werden.
preOrder( N, callback, param) { // Startknoten N
// Führe die gewünschten Aktionen am Knoten aus:
callback( N, param );
if ( N.links ≠ null )
preOrder( N.links ); // rekursiver Aufruf
if ( N.rechts ≠ null )
preOrder( N.rechts ); // rekursiver Aufruf
}
postOrder( N, callback, param) {
if ( N.links ≠ null )
postOrder( N.links ); // rekursiver Aufruf
if ( N.rechts ≠ null )
postOrder( N.rechts ); // rekursiver Aufruf
// Führe die gewünschten Aktionen am Knoten aus:
callback( N, param );
}
inOrder( N, callback, param) {
if ( N.links ≠ null )
inOrder( N.links ); // rekursiver Aufruf
// Führe die gewünschten Aktionen am Knoten aus:
callback( N, param );
if ( N.rechts ≠ null )
inOrder( N.rechts ); // rekursiver Aufruf
}
revOrder( N, callback, param) {
if ( N.rechts ≠ null )
revOrder( N.rechts ); // rekursiver Aufruf
// Führe die gewünschten Aktionen am Knoten aus:
callback( N, param );
if ( N.links ≠ null )
revOrder( N.links ); // rekursiver Aufruf
}
Eine Traversierung über den ganzen Baum umfasst pro Knoten genau einen Aufruf einer der rekursiven Traversierungs-Funktionen. Der Aufwand (für die reine Traversierung) bei Knoten ist also in .
Iterative Implementierung
Eine iterative Implementierung erlaubt es, einen einzelnen Querungs-Schritt, eine „Iteration“, von einem Knoten zu seinem Nachbarknoten auszuführen. So kann man in gewohnter Manier eine Programmschleife für ein Intervall mit Anfang und Ende aufsetzen, die fraglichen Knoten nacheinander aufsuchen und für sie die gewünschten Aktionen ausprogrammieren.[3]
Als Beispiel sei hier nur die in-order-Traversierung gezeigt, die insbesondere bei binären Suchbäumen eine große Rolle spielt, da diese Reihenfolge der Sortier-Reihenfolge entspricht.
inOrderNext( N, richtung ) { // Startknoten N
// richtung = 1 (Rechts = aufwärts = „in-order“)
// oder = 0 (Links = abwärts = „reverse in-order“)
Y = N.kind[richtung]; // 1 Schritt in die gegebene Richtung
if ( Y ≠ null ) {
gegenrichtung = 1 - richtung; // spiegele Links <-> Rechts
// Abstieg zu den Blättern über Kinder in der gespiegelten Richtung:
Z = Y.kind[gegenrichtung];
while ( Z ≠ null ) {
Y = Z;
Z = Y.kind[gegenrichtung];
}
return Y; // Ergebnisknoten: Blatt oder Halbblatt
}
// Aufstieg zur Wurzel über die Vorfahren der gegebenen Kindesrichtung:
Y = ;
do {
Z = Y;
Y = Z.elter;
if ( Y = null )
return null; // Knoten Z ist die Wurzel:
// d. h. es gibt kein Element mehr in dieser Richtung
} until ( Z ≠ Y.kind[richtung] );
// Y ist der erste Vorfahr in der gespiegelten Richtung
return Y; // Ergebnisknoten
}
Eine Traversierung über den ganzen Baum beinhaltet pro Kante einen Abstieg (in der Richtung der Kante) und einen Aufstieg (in der Gegenrichtung). Ein Baum mit Knoten hat Kanten, so dass eine Gesamttraversierung über Stufen geht. Der Aufwand für eine Einzel-Traversierung ist also im Mittel in und im schlechtesten Fall in mit als der Höhe des Baums.
Breitensuche
breadth-first oder level-order:
Beginnend bei der Baumwurzel werden die Ebenen von links nach rechts durchlaufen.
Abstieg zum ersten oder letzten Element
Ganz ähnlich wie eine iterative Tiefensuche funktioniert die Suche nach dem ersten oder letzten Element.
firstLast( binärBaum, richtung ) {
// richtung = Links (erstes) oder Rechts (letztes)
Y = binärBaum.wurzel;
if ( Y = null )
return null; // der Baum ist leer
// Abstieg zu den (Halb-)Blättern
do {
Z = Y;
Y = Z.kind[richtung];
} while ( Y ≠ null );
return Z; // Blatt oder Halbblatt
Der Aufwand ist , wo die Höhe des Baums ist.
Einfügen, Einfügepunkt
Es sei angenommen, dass die Navigation zu einem Einfügepunkt bereits erfolgt ist. Einfügepunkt bedeutet einen Knoten und eine Richtung (rechts bzw. links). Ein unmittelbarer Einfügepunkt in einem binären Baum ist immer ein rechtes (bzw. linkes) Halbblatt, ein mittelbarer ist der unmittelbare Nachbar in der angegebenen Richtung und spezifiziert zusammen mit der Gegenrichtung dieselbe Stelle im Binärbaum – zum echten Einfügen muss aber die Einfügefunktion noch bis zu dem Halbblatt hinabsteigen, welches den unmittelbaren Einfügepunkt darstellt.
Zum Einfügen lässt man das Kind auf der geforderten Richtung des Knotens auf das neue Element verweisen, damit ist dieses korrekt eingefügt. Die Komplexität der Einfügeoperation ist somit konstant.
Nach dem Einfügen ist das neue Element ein Blatt des Binärbaums.
Im folgenden Beispiel wird ein Knoten mit dem Schlüssel J in einen binären Baum am (unmittelbaren) Einfügepunkt (M, links) eingefügt – der mittelbare wäre (G, rechts).
S S / \ / \ / \ / \ G W G W / \ / \ / \ ----> / \ D M D M / \ \ / \ / \ B F P B F J P
Durch wiederholtes Einfügen an immer derselben Stelle kann es dazu kommen, dass der Baum zu einer linearen Liste entartet.
Löschen
Beim Löschen muss man deutlich mehr Fälle unterscheiden. Wichtig ist z. B., wie viele Kinder der Knoten hat.
Fall A: Zu löschender Knoten hat höchstens ein Kind.
Ist der Knoten ein Blatt (Knoten ohne Kinder), dann wird beim Löschen einfach der Knoten entfernt. Hat der zu löschende Knoten genau ein Kind, wird dieses an die Stelle des zu löschenden Knotens gesetzt.
Fall B: Zu löschender Knoten hat zwei Kinder.
In diesem Fall kann die Löschung sowohl über den linken wie über den rechten Teilbaum vollzogen werden. Um die in-order-Reihenfolge aufrechtzuerhalten, ist aber ein Abstieg bis zu einem Halbblatt unvermeidlich.
Eine Möglichkeit ist, den linken Teilbaum an die Position zu setzen, an der der zu löschende Knoten war, und den rechten Teilbaum an den linken an dessen rechtester Stelle anzuhängen, wie es das Beispiel zeigt (G soll gelöscht werden):
S S
/ \ / \
/ \ / \
G W D W
/ \ / \
/ \ ----> / \
D M B F
/ \ / \ \
B F J P M
\ / \
K J P
\
K
Die Veränderungen in den Höhen fallen jedoch kleiner aus, wenn der zu löschende Knoten durch einen (unmittelbaren) Nachbarn in der in-order-Reihenfolge ersetzt wird.[4] Im Beispiel ist F der linke Nachbar von G, steht also im linken Teilbaum ganz rechts; J ist der rechte Nachbar von G, steht also im rechten Teilbaum ganz links. Die in-order-Reihenfolge ist F – G – J. Der linke/rechte Nachbar kann einen linken/rechten Teilbaum haben, der an die Stelle gehängt werden muss, wo der Nachbar war.
Im folgenden Beispiel wird der zu löschende Knoten G durch seinen rechten Nachbarn J ersetzt:
S S
/ \ / \
/ \ / \
G W J W
/ \ / \
/ \ / \
D M ----> D M
/ \ / \ / \ / \
B F J P B F K P
\
K
Um dem Baum möglichst wenig Gelegenheit zu geben, einseitig zu werden, kann man systematisch zwischen linkem und rechtem Abstieg abwechseln. Stehen Balance-Werte zur Verfügung, liegt es nahe, den Abstieg auf der evtl. höheren Seite zu bevorzugen.
Durch wiederholtes Löschen kann es dazu kommen, dass der Baum zu einer linearen Liste entartet.
Wegen der unvermeidlichen Abstiege bis zu den Halbblättern ist die Komplexität der Löschoperation im schlechtesten Fall , wobei die Höhe des Baumes ist. Da der Abstieg einer Einzel-Traversierung entspricht und Abstiege in einer Gesamttraversierung gleich häufig sind wie Aufstiege, konvergiert der Mittelwert der abzusteigenden Ebenen für wachsende Anzahl der Knoten genau gegen 1.
Die Abbildungen und der Pseudocode zeigen das Entfernen eines Elements, das zwei Kinder und einen nahen Enkel besitzt, aus einem binären Baum.
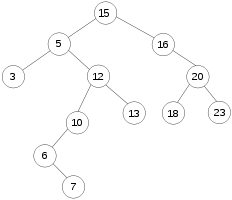Der Knoten 5 soll gelöscht werden
Der neue Baum
- Pseudocode
remove( binärBaum, knoten ) {
// Es sei angenommen, dass knoten.links ≠ null, knoten.rechts ≠ null
// und knoten.rechts.links ≠ null
knotenY = knoten.rechts;
while ( knotenY ≠ null ) {
knotenZ = knotenY;
knotenY = knotenZ.links;
}
// knotenZ ist der rechte Nachbar von knoten
if ( knotenZ.rechts ≠ null )
knotenZ.rechts.elter = knotenZ.elter;
knotenZ.elter.links = knotenZ.rechts;
knotenZ.rechts = knoten.rechts;
knoten.rechts.elter = knotenZ;
knotenZ.links = knoten.links;
knoten.links.elter = knotenZ; // knoten.links ≠ null
if ( knoten.elter.links = knoten )
knoten.elter.links = knotenZ;
else
knoten.elter.rechts = knotenZ;
knotenZ.elter = knoten.elter;
}
Rotation
Mit einer Rotation (вращение (russ. für Drehung) bei Adelson-Velsky und Landis[5]) kann man einen Binärbaum in einen anderen überführen und damit Eigenschaften, insbesondere Höhen von Teilbäumen (beispielsweise in Rot-Schwarz-Bäumen und AVL-Bäumen) oder Suchtiefen von Knoten (beispielsweise in Splay-Bäumen) beeinflussen. Da bei einer Rotation alle beteiligten Knoten sich nur „vertikal“ bewegen, ändert sich die in-order-Reihenfolge nicht, so dass der Baum bezüglich dieser Reihenfolge (die bei Suchbäumen die Sortierfolge ist) äquivalent bleibt.
Eine Rotation lässt sich durch die Rotationsrichtung Links oder Rechts und durch die Wurzel des betroffenen Teilbaums spezifizieren. Statt der beiden kann auch ein Kindknoten angegeben werden, der in dieser Verwendung als der Pivot (Drehpunkt) der Rotation bezeichnet wird. Dabei ist die Rotationsrichtung der Kindesrichtung entgegengesetzt. Zum Beispiel bewirkt RotateLeft(L) die Absenkung des Knotens L und die Anhebung seines rechten Kindknotens (hier als Pivot: R). Es handelt sich aber nicht um eine kontinuierliche Drehung, eher um eine bistabile Wippe, also das Kippen einer Kante (hier: L↘R) in ihre andere Orientierung (L↙R). Die Anforderungen
- Umkehrung der Orientierung einer gerichteten Kante
- Bewahrung der in-order-Reihenfolge
- kleinstmögliche Veränderung des Baums
ziehen gewisse Anpassungen bei den Nachbarknoten nach sich, nämlich: (unten) das Einhängen des zwischen den beiden Knoten befindlichen Kindes (hier: m) als inneres Kind am unteren Knoten und (oben) das Ersetzen des bisherigen Kindes beim (Groß-)Elter (hier: P) durch den oberen Knoten.[6]
.gif)
P P
/ /
L RotateLeft(L) R
/ \ --------> / \
l \ <-------- / r
R RotateRight(R) L
/ \ / \
m r l m
- Erklärung zu RotateLeft(L)
L wird zum linken Kind von R. Der ursprünglich linke Kindbaum m von R (der Teilbaum in der Mitte) wird zum rechten Kindbaum von L.
- Erklärung zu RotateRight(R)
R wird zum rechten Kind von L. Der ursprünglich rechte Kindbaum m von L wird zum linken Kindbaum von R.
Komplexität
In beiden Fällen ändert sich zusätzlich die Aufhängung des neuen Baums von oben her. Die Aufhängungen der äußeren Kindbäume l und r bleiben erhalten.
Somit sind 3 Verknüpfungen anzupassen, die in den Graphiken verstärkt gezeichnet sind. Im Ergebnis benötigt eine Rotation konstante Laufzeit .
Doppelrotation
Eine Doppelrotation besteht aus zwei unmittelbar hintereinander ausgeführten gegenläufigen (Einzel)rotationen. Dabei wird ein Knoten um zwei Ebenen angehoben. Sie wird bspw. bei der Rebalancierung von AVL-Bäumen benötigt. Die Anzahl der anzupassenden Verknüpfungen ist 5.
Beim Spalten eines AVL-Baums können auch Dreifachrotationen vorkommen.
Rotationsmetrik
Der Rotationsabstand zwischen 2 Binärbäumen mit derselben Anzahl von Knoten ist die Minimalzahl an Rotationen, die erforderlich sind, um den ersten Baum in den zweiten zu überführen. Mit dieser Metrik wird die Menge der Binärbäume mit Knoten zu einem metrischen Raum, denn die Metrik erfüllt Definitheit, Symmetrie und Dreiecksungleichung. Der Raum ist ein zusammenhängender metrischer Raum mit einem Durchmesser .[7] Das heißt: Zu 2 verschiedenen Binärbäumen und gibt es eine natürliche Zahl und Binärbäume , so dass mit und für jeweils aus durch eine Rotation hervorgeht.
Es ist ungeklärt, ob es einen polynomiellen Algorithmus zur Berechnung des Rotationsabstands gibt.
Umwandeln einer Form eines Binärbaums in eine andere
Bei den folgenden Umwandlungen wird die in-order-Reihenfolge nicht geändert. Ferner sei die Anzahl der Knoten im Baum.
- Ein Binärbaum lässt sich mit Aufwand für Platz und Zeit in eine geordnete Liste umwandeln.
- Da das Eintragen eines einzelnen Eintrags in eine geordnete Liste konstanten Aufwand bedeutet, ist angesichts der Komplexität der #Traversierung linearer Aufwand leicht zu schaffen. Schwieriger ist es, das Eintragen in-place zu bewerkstelligen, also den Platz für die Zeiger der Liste vom Platz für den Binärbaum zu nehmen.
- Eine geordnete Liste lässt sich mit Zeitaufwand in einen vollständig balancierten Binärbaum umwandeln.
- Die Form eines vollständig balancierten Binärbaums hängt nur von seiner Knotenzahl ab. Ist ein Teilbaum mit einer lückenlosen Folge von Knoten aufzubauen, dann ordnet man dem linken Kindbaum eine lückenlose Folge von und dem rechten eine von Knoten zu. Damit weichen die Abstände zweier beliebiger Blätter von der Wurzel um höchstens 1 voneinander ab, wie es sein muss.
- In einem Binärbaum lässt sich mit dem Zeitaufwand jeder Knoten mit der Anzahl der Knoten in seinem Teilbaum versehen.
- Bei der Traversierung kann man die Knotenzahlen pro Teilbaum bilden und im Knoten abspeichern.
- Ein AVL-Baum lässt sich ohne Änderung seiner Form mit Zeitaufwand als Rot-Schwarz-Baum einfärben.
- Die Menge der AVL-Bäume ist eine echte Teilmenge in der Menge der Rot-Schwarz-Bäume. Der dortige Beweis zeigt nebenbei, dass man anhand der Höhen, die man beim in-order-Durchlauf exakt mitschreibt, die Rot-Schwarz-Einfärbung vornehmen kann.
Siehe auch
Literatur
- Donald Knuth: The art of computer programming vol 1. Fundamental Algorithms. 3. Auflage. Addison-Wesley, 1997, ISBN 0-201-89683-4, Abschnitt 2.3, S. 318 ff.
- Horst Wettstein: Systemprogrammierung. 2. Auflage. Carl Hanser Verlag, 1980, ISBN 3-446-13217-1.
- Lennart Krothaus: Der Binärbaum-Ein Informatikwunder. 3. Auflage. MethiVerlag, 1998.
- Robert Sedgewick, Kevin Wayne: Algorithms Fourth Edition. (PDF) Pearson Education, 2011, ISBN 978-0-321-57351-3.
Weblinks
- Ben Pfaff: An Introduction to Binary Search Trees and Balanced Trees. (PDF; 1675 kB) 2004 (englisch).
Einzelnachweise
- Die Höhe kommt betragsmäßig damit auf denselben Wert wie Knuth, der neben den Schlüssel tragenden Knoten (bei ihm „innere“ genannt) noch „äußere“ Knoten kennt, die als Einfügepunkte aufgefasst werden können und die die Höhe (der ersten Definition entsprechend) um 1 erhöhen.
- Die Bezeichnungen finden sich bspw. bei Knuth.
- S. a. Pfaff 2004, p.58 „4.9.3.7 Advancing to the Next Node“ mit einem Stapelspeicher, genannt „Traverser“, für den Rückweg zur Wurzel. Die vorgestellte Lösung kommt ohne aus – sie setzt stattdessen einen Zeiger
elterzum Elterknoten voraus. - Da zwischen den beiden Knoten kein weiterer Knoten liegen kann, wird die in-order-Reihenfolge nicht verändert. Diese Vorgehensweise wurde zum ersten Mal 1962 von T. Hibbard vorgeschlagen (zitiert nach #Sedgewick S. 410.)
- G. M. Adelson-Velsky, E. M. Landis: Один алгоритм организации информации. In: Doklady Akademii Nauk SSSR. 146, 1962, S. 263–266. (russisch)
- Die Eindeutigkeit dieser Anpassungen ist (nur) bei den binären Bäumen gegeben. Denn wenn eine Kante L→R gekippt wird, muss am vorher unteren Knoten R eine „Valenz“ für das neue Kind L frei gemacht werden. Die einzige in der korrekten Richtung ist die Valenz für m. Bei L wird gleichzeitig eine Valenz (die vorher auf R zeigte) frei, die die Richtung von m hat und m übernehmen muss. Ganz ähnlich verhält es sich am oberen Ende der Kante.
- Daniel D. Sleator, Robert E. Tarjan, William P. Thurston: Rotation distance, triangulations, and hyperbolic geometry. In: Journal of the American Mathematical Society, 1, (3), 1988, S. 647–681.