Out-Tree
Ein Out-Tree ist in der Graphentheorie ein spezieller Graph, genauer ein gewurzelter Baum, bei dem die Kanten von der Wurzel ausgehen.
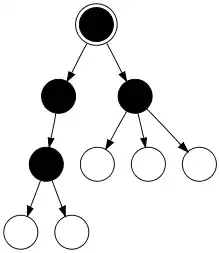
Definition
Ein Out-Tree ist ein gerichteter Graph mit einem ausgezeichneten Knoten, der so genannten Wurzel, für den im Gegensatz zu In-Trees gilt, dass jeder Knoten durch genau einen gerichteten Pfad von der Wurzel aus erreichbar ist.
Weitere Begriffe
Der maximale Ausgangsgrad wird als Ordnung eines Out-Trees bezeichnet und alle Knoten mit Ausgangsgrad 0 bezeichnet man als Blätter. Als Tiefe eines Knotens bezeichnet man die Länge des Pfades von der Wurzel zu ihm und als Höhe des Out-Trees die Länge eines längsten Pfades.
Wie bei ungerichteten Bäumen bezeichnet man auch in gewurzelten Bäumen alle Knoten, die kein Blatt sind, als innere Knoten. Manchmal schließt man die Wurzel dabei aber aus.
Bei einem (a,b)-Baum haben alle Teilbäume die gleiche Tiefe.
Für einen von der Wurzel verschiedenen Knoten v bezeichnet man den Knoten, durch den er mit einer eingehenden Kante verbunden ist als Vater, Vaterknoten, Elternknoten oder Vorgänger von v. Als Vorfahren von v bezeichnet man alle Knoten, die entweder Vater von v oder Vorgänger des Vaters sind.
Umgekehrt bezeichnet man alle Knoten, die von einem beliebigen Knoten v aus durch eine ausgehende Kante verbunden sind als Kinder, Kindknoten, Sohn oder Nachfolger von v. Als Nachfahren von v bezeichnet man Kinder von v oder deren Nachfahren. Als Geschwister oder Geschwisterknoten werden in einem Out-Tree Knoten bezeichnet, die denselben Vater besitzen.
Alternative Definition
Out-Trees lassen sich auch rekursiv definieren. Sie bestehen aus einem Knoten w, der die Wurzel des Baumes darstellt, welcher ausschließlich mit den Wurzeln knotendisjunkter Out-Trees T1, T2, ..., Tn verbunden ist, und zwar in Richtung der Wurzeln von T1, T2, ..., Tn.