Stapelspeicher
In der Informatik bezeichnet ein Stapelspeicher oder Kellerspeicher (kurz Stapel oder Keller, häufig auch mit dem englischen Wort Stack bezeichnet) eine häufig eingesetzte dynamische Datenstruktur. Sie wird von den meisten Mikroprozessoren direkt mithilfe von Maschinenbefehlen unterstützt.

Funktionsprinzip
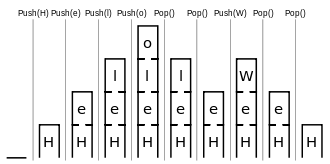
Ein Stapel kann eine theoretisch beliebige, in der Praxis jedoch begrenzte Menge von Objekten aufnehmen. Elemente können nur oben auf den Stapel gelegt und auch nur von dort wieder gelesen werden. Elemente werden übereinander gestapelt und in umgekehrter Reihenfolge vom Stapel genommen. Dies wird auch Last-In-First-Out-Prinzip (LIFO) genannt.
Dazu werden folgende Operationen zur Verfügung gestellt:
- push (auch „einkellern“)
- legt das Objekt oben auf den Stapel.
- pop („auskellern“)
- liefert das oberste Objekt und entfernt es vom Stapel. Bei manchen Prozessoren wie dem MOS Technology 6502 wird diese Aktion dagegen pull („herunterziehen“) genannt.
- peek („nachsehen“)
- liefert das oberste Objekt, ohne es zu entfernen (zuweilen auch top genannt, also „oben“).
In der Automatentheorie werden Stapel benutzt, um bestimmte Problemklassen theoretisch betrachten zu können (siehe Kellerautomat). Sie unterscheidet deshalb genauer zwischen einem echten Kellerspeicher, bei dem kein Element außer dem obersten gelesen werden kann, und einem Stapelspeicher, bei dem jedes Element betrachtet, aber nicht verändert werden kann. In der Praxis spielt diese Unterscheidung jedoch kaum eine Rolle; beinahe jede Implementierung ist ein Stapel. Daher werden die Begriffe im Allgemeinen synonym verwendet.
Es gibt viele Variationen des Grundprinzips von Stapeloperationen. Jeder Stapel hat einen festen Speicherort im Speicher, an dem er beginnt. Wenn Datenelemente zum Stapel hinzugefügt werden, wird der Stapelzeiger verschoben, um die aktuelle Ausdehnung des Stapels anzuzeigen, die sich vom Ursprung weg ausdehnt.
Stapelzeiger können auf den Ursprung eines Stapels oder auf einen begrenzten Adressbereich entweder über oder unter dem Ursprung zeigen, abhängig von der Richtung, in die der Stapel wächst. Der Stapelzeiger kann jedoch den Ursprung des Stapels nicht überschreiten. Mit anderen Worten, wenn der Ursprung des Stapels bei der Speicheradresse 1000 liegt und der Stapel nach unten in Richtung der Speicheradressen 999, 998 usw. wächst, darf der Stapelzeiger niemals über 1000 auf 1001, 1002 usw. hinaus erhöht werden. Wenn eine Pop-Operation auf dem Stapel bewirkt, dass sich der Stapelzeiger über den Ursprung des Stapels hinaus bewegt, tritt ein Stapelunterlauf auf. Wenn eine Push-Operation bewirkt, dass der Stapelzeiger über die maximale Ausdehnung des Stapels hinaus erhöht oder verringert wird, tritt ein Stapelüberlauf auf.
Einige Laufzeitumgebungen, die stark von Stapeln abhängig sind, bieten möglicherweise zusätzliche Vorgänge, zum Beispiel
duplicate („duplizieren“)
Das oberste Element wird eingeblendet und dann erneut gedrückt (zweimal), sodass jetzt eine zusätzliche Kopie des vorherigen obersten Elements mit dem Original darunter oben liegt.
swap oder exchange („tauschen“)
Die beiden obersten Gegenstände auf dem Stapel tauschen Plätze aus.
rotate oder roll („rotieren“)
Die n obersten Elemente werden rotierend auf dem Stapel verschoben. Wenn beispielsweise n = 3 ist, werden die Elemente 1, 2 und 3 auf dem Stapel an die Positionen 2, 3 bzw. 1 auf dem Stapel verschoben. Viele Varianten dieser Operation sind möglich, wobei die häufigste als Linksdrehung und Rechtsdrehung bezeichnet wird.
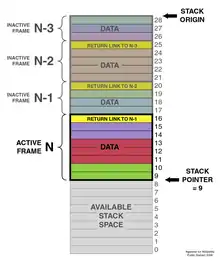
Stapel werden oft so dargestellt, dass sie von unten nach oben wachsen. Sie können auch visualisiert werden, wie sie von links nach rechts wachsen, so dass "ganz oben" zu "ganz rechts" wird, oder sogar von oben nach unten wachsen. Das wichtige Merkmal ist, dass sich der Boden des Stapels in einer festen Position befindet. Die Abbildung in diesem Abschnitt ist ein Beispiel für eine Wachstumsvisualisierung von oben nach unten: Die Oberseite (28) ist der Stapel "unten", da der Stapel "oben" (9) der Ort ist, an dem Elemente geschoben oder herausgeschoben werden.
Ein Stapel wird in Computern normalerweise durch einen Block von Speicherzellen dargestellt, wobei sich der "untere" an einer festen Stelle befindet und der Stapelzeiger die Speicheradresse der aktuellen "oberen" Zelle im Stapel enthält. Die obere und untere Terminologie werden verwendet, unabhängig davon, ob der Stapel tatsächlich in Richtung niedrigerer Speicheradressen oder in Richtung höherer Speicheradressen wächst.
Wenn Sie ein Element auf den Stapel schieben, wird der Stapelzeiger um die Größe des Elements angepasst, also entweder dekrementiert oder inkrementiert, abhängig von der Richtung, in der der Stapel im Speicher wächst, indem er auf die nächste Speicherzelle zeigt und das neue oberste Element in kopiert der Stapelbereich. Abhängig von der genauen Implementierung kann der Stapelzeiger am Ende einer Push-Operation auf die nächste nicht verwendete Position im Stapel oder auf das oberste Element im Stapel zeigen. Wenn der Stapel auf das aktuell oberste Element zeigt, wird der Stapelzeiger aktualisiert, bevor ein neues Element auf den Stapel verschoben wird. Wenn es auf die nächste verfügbare Position im Stapel zeigt, wird es aktualisiert, nachdem das neue Element auf den Stapel verschoben wurde.
Illustration
Ein Stapelspeicher ist mit einem Stapel von Umzugskisten vergleichbar. Es kann immer eine neue Kiste oben auf den Stapel gepackt werden (entspricht push) oder eine Kiste von oben heruntergenommen werden (entspricht pop). Der Zugriff ist im Regelfall nur auf das oberste Element des Stapels möglich. Ein Hinzufügen oder Entfernen einer Kiste weiter unten im Stapel ist nicht möglich. Es gibt aber in manchen Implementierungen Befehle, um die obersten Elemente zu vertauschen (SWAP, ROT).
Geschichte
Die Verwendung eines Stapelspeichers zur Übersetzung von Programmiersprachen wurde 1957 von Friedrich L. Bauer und Klaus Samelson unter dem Namen „Kellerprinzip“ patentiert[1][2] und etwa zur selben Zeit unabhängig vom australischen Philosophen Charles Hamblin entwickelt. Die lange ausgebliebene internationale Anerkennung und Ehrung ihrer Leistung erfolgte erst im Jahr 1988. Bauer erhielt den renommierten Computer Pioneer Award (IEEE) für Computer Stacks. Samelson war bereits 1980 verstorben.
Anwendungen
Mit Stapelspeichern kann man Terme und Syntaxen einfach auf richtige Verschachtelung prüfen. Dies wird oft z. B. bei der Verarbeitung von BB-Codes und XML-Dokumenten benötigt.
Mikroprozessoren
In Mikroprozessoren gibt es oft ein spezielles Register, den Stackpointer (Stapelzeiger). Dieses Register enthält eine Speicheradresse, die auf den aktuellen Stapeleintrag (des aktuellen Prozesses) zeigt. Viele Befehle/Operationen des Mikroprozessors nutzen diesen Stapeleintrag. Unter anderem gibt es Befehle, mit denen man in den Stack schreiben (z. B. push beim x86-Prozessor) oder von ihm lesen kann (z. B. pop). Dabei wird automatisch der Stapelzeiger verringert oder erhöht.
Die Operation Jump To Subroutine (Sprung in ein Unterprogramm) legt auf dem Stack die Rücksprungadresse ab, die später von der Operation Return From Subroutine verwendet wird. Unterprogrammen bzw. Funktionen, wie man sie aus Programmiersprachen wie C kennt, werden die Parameter über den Stack übergeben, der auch die Rückgabewerte aufnimmt. Außerdem werden lokale Variablen auf dem Stack gespeichert. Dies erlaubt unter anderem Rekursion, das Aufrufen einer Funktion aus ebendieser Funktion heraus. Wird bei der Rückkehr aus einer Funktion nur ein Eintrag zu viel oder zu wenig ausgelesen, führt dies zu besonders gravierenden Programmfehlern, da der Prozessor dann versuchen wird, Code an völlig zufälliger Speicherposition auszuführen. Durch das Ausnutzen einer nicht korrekt behandelten Größenangabe der Daten können Angreifer versuchen, einen Pufferüberlauf zu produzieren, der den Stack so verändert, dass durch Umleiten des Rücksprungs bösartiger Code ausgeführt wird.
Bei den meisten Prozessoren beginnt der Stapel bei einer hohen Adresse und wird in Richtung der Adresse 0 gestapelt. Das bedeutet, dass bei push der Stapelzeiger vermindert und etwas in den Stack geschrieben wird und bei pop vom Stack gelesen und der Stapelzeiger erhöht wird. Der Stapel wächst „nach unten“, in Richtung niedrigerer Speicheradressen. Dies ist historisch begründet: Legt man bei begrenztem Speicher den Stack unterhalb des Speicherplatzes, der von den Programmen benutzt wird, können so andere Programmdaten, die normal hinter dem Programm abgelegt werden, den Stapel nicht so leicht überschreiben und der Stapel nicht das Maschinenprogramm. Des Weiteren kann so das oberste Element auf dem Stapel immer mit dem Offset Null (relativ zum Stapelzeiger) adressiert werden und das Hinzufügen eines Elements auf dem Stack ist möglich ohne die Größe des bisher obersten Elements zu kennen.
In Multitasking-Systemen gibt es für jeden Prozess und innerhalb der Prozesse für jeden Thread einen eigenen Stapelspeicher. Beim Umschalten zwischen Prozessen bzw. Threads wird neben anderen Registern auch der jeweilige Stapelzeiger gespeichert und geladen.
Um Fehler in der Benutzung des Stacks durch einen „Unterlauf“ des Stapelzeigers aufzudecken, legen manche Betriebssysteme wie beispielsweise DOS oder CP/M (bei COM-Programmen) oder OSEK-OS als untersten Wert im Stapel die Sprungadresse einer Abbruch- oder Fehlerbehandlungsroutine ab. Holt der Prozessor durch einen Fehler in der Aufrufverschachtelung diese Adresse vom Stapel, kann gegebenenfalls noch auf den Ablauffehler reagiert werden. Manche Betriebssysteme können auch den Stapelspeicher während der Laufzeit vergrößern, was bei einem bereits sehr großen Stapel relativ viel Zeit in Anspruch nehmen kann. Bei anderen Betriebssystemen hat der Programmierer selbst anzugeben, wie groß der Stack sein soll.
Um den Nutzungsgrad des meist begrenzten Stapelspeichers zu ermitteln, bedient man sich der sogenannten Wasserstands-Methode: Der gesamte für den Stapelspeicher reservierte Speicher wird mit einem fixen Datenmuster initialisiert und dann das Programm gestartet. Anhand der Bereiche, die nach einer gewissen Laufzeit noch das Initialisierungsmuster enthalten, kann festgestellt werden, wie viel Platz auf dem Stapel wirklich genutzt wurde.
Abstrakter Datentyp
Bei der Implementierung eines Stapelspeichers als abstrakter Datentyp in einer einfach verketteten Liste wird der Zeiger auf Daten gespeichert, anstelle die Daten in jedem Knoten zu speichern. Das Programm weist den Speicher für die Daten zu und die Speicheradresse wird an den Stapelspeicher übergeben. Der Kopfknoten und die Datenknoten sind im abstrakten Datentyp gekapselt. Eine aufgerufene Funktion kann nur den Zeiger auf den Stapelspeicher sehen. Der Datentyp enthält auch einen Zeiger auf die Oberseite und den Zähler für die Anzahl der Elemente im Stapel.[3]
struct StackNode {
void *dataPointer;
StackNode *link;
};
struct Stack {
int count;
StackNode *top;
};
Programmierung
Compiler bzw. Interpreter für Programmiersprachen nutzen gewöhnlich push-Operationen vor dem Aufruf eines Unterprogramms, um an dieses Parameter zu übergeben. Weil der Compiler die Typen der Parameter kennt, können sie unterschiedliche Größen haben. Ähnlich können so auch Ergebnisse des Unterprogramms zurückgegeben werden. Für lokale Variablen des Unterprogramms wird dieser Mechanismus nochmal erweitert, indem auch für sie auf dem Stapelspeicher Platz reserviert wird. Dadurch wird das Unterprogramm dann rekursiv aufrufbar. Bei der Umwandlung eines rekursiven Unterprogramms in ein iteratives Unterprogramm muss dieser Mechanismus häufig explizit implementiert werden.
Programmiersprachen, die auf eine prozessbasierte virtuelle Maschine aufsetzen, zum Beispiel Java, P-Code-Pascal, optimieren den kompilierten Zwischencode für die Verwendung eines Stapels, um zur Laufzeit die Interpretation dieses Zwischencodes zu beschleunigen.
C++
Implementierung eines Stacks in der Programmiersprache C++ mit einer einfach verketteten Liste:[4][5]
#include <memory>
#include <stdexcept>
#include <utility>
using namespace std;
template <typename T>
class stack {
struct item {
T value;
unique_ptr<item> next = nullptr;
item(T& _value): value(_value) {}
};
unique_ptr<item> _peek = nullptr;
size_t _size = 0;
public:
// erzeugt einen leeren Stack
stack() {}
// erzeugt einen Stack mit n Elementen von T
stack(size_t n, T _value) {
for (size_t i = 0; i < n; ++i)
push(_value);
}
// Kopierkonstruktor
stack(stack<T>& rhs) {
*this = rhs;
}
// Zuweisungsoperator
stack& operator=(stack<T>& rhs) {
// Überprüfe ob ein Stack sich selbst zugewiesen wird
if (this == &rhs)
return *this;
item* traverse = rhs._peek.get();
// Absteigen zum ersten Element, dann zum zweiten etc.
while (traverse != nullptr) {
push(traverse->value);
traverse = traverse->next.get();
}
return *this;
}
void push(T& _value) {
unique_ptr<item> temp = make_unique<item>(_value);
temp.swap(_peek);
// next des letzten Stackelements ist ein nullptr
_peek->next = move(temp);
_size++;
}
T pop() {
if (_peek == nullptr)
throw underflow_error("Nothing to pop.");
T value = _peek->value;
_peek = move(_peek->next);
_size--;
return value;
}
T& peek() {
if (_peek == nullptr)
throw underflow_error("Nothing to peek.");
return _peek->value;
}
size_t size() {
return _size;
}
};
C
Implementierung eines Stacks in der Programmiersprache C mit einem Array:
#include <stdbool.h>
#include <stddef.h>
#define LEN 100
int data[LEN];
size_t count = 0;
bool is_empty() {
return count == 0;
}
bool is_full() {
return count == LEN;
}
void push(int value) {
if (is_full())
return;
data[count] = value;
count++;
}
int pop() {
if (is_empty())
return 0;
count--;
return data[count];
}
int peek() {
if (is_empty())
return 0;
return data[count - 1];
}
size_t size() {
return count;
}
Java
Implementierung eines Stacks in der Programmiersprache Java mit einer einfach verketteten Liste:[6]
class Stack<T> {
private class Item {
T value; // Das zu verwaltende Objekt
Item next; // Referenz auf den nächsten Knoten
Item(T value, Item next) {
this.value = value;
this.next = next;
}
}
private Item peek;
// Prüft, ob der Stapel leer ist
public boolean empty() {
return this.peek == null;
}
// Speichert ein neues Objekt
public void push(T value) {
this.peek = new Item(value, this.peek);
}
// Gibt das oberste Objekt wieder und entfernt es aus dem Stapel
public T pop() {
T temp = this.peek.value;
if (!empty())
this.peek = this.peek.next;
return temp;
}
// Gibt das oberste Objekt wieder
public T peek() {
return !empty() ? this.peek.value : null;
}
}
Python
Implementierung eines Stacks in der Programmiersprache Python mit einer dynamisch erweiterbaren Liste:
class Stack:
_data = []
def is_empty(self):
return len(self._data) == 0
def push(self, element):
self._data.append(element)
def pop(self):
if self.is_empty():
return None
return self._data.pop()
def peek(self):
if self.is_empty():
return None
return self._data[-1]
def __str__(self):
return self._data.__str__()
def main():
my_stack = Stack()
print(my_stack.is_empty())
my_stack.push(5)
my_stack.push(3)
print(my_stack.is_empty())
print(my_stack)
print(my_stack.peek())
my_stack.pop()
print(my_stack.peek())
if __name__ == "__main__":
main()
In vielen Programmiersprachen sind Stacks bereits in der Standardbibliothek implementiert. So stellt Java diese Funktionalität in der Klasse java.util.LinkedList zur Verfügung. In der C++ Standard Template Library bietet das Template stack<T> entsprechende Funktionalität, welche normalerweise jedoch anders als hier nicht mit einer verketteten Liste implementiert ist.
Beispiel mit Spielkarten
Das folgende Beispiel in der Programmiersprache C++ zeigt die Implementierung von einem Stapel aus Spielkarten mit einem Stack in der Methode main. Dabei wird die Klasse stack der Programmbibliothek von C++ verwendet.[7]
Kartenspiele und Gesellschaftsspiele, bei denen während dem Spiel Karten auf einen Stapel gelegt oder von einem Stapel gezogen wird, zum Beispiel Texas Hold’em, Omaha Hold’em, Canasta und Die Siedler von Catan, können sinnvoll mithilfe von Stacks programmiert werden.
// Bindet den Datentyp stack in das Programm ein
#include <stack>
#include <iostream>
using namespace std;
int main()
{
// Initialisiert einen Stapel mit dem Elementtyp string
auto myStack = stack<string>();
// Legt nacheinander 3 Elemente auf den Stapel
myStack.push("Kreuz Bube");
myStack.push("Herz Dame");
myStack.push("Karo König");
// Ausgabe auf der Konsole ("Karo König")
cout << "Die Höhe des Stapels ist " << myStack.size()
<< " und die oberste Karte des Stapels ist " << myStack.top() << endl;
// Entfernt das oberste Element ("Karo König")
myStack.pop();
// Ausgabe auf der Konsole ("Herz Dame")
cout << "Die Höhe des Stapels ist " << myStack.size()
<< " und die oberste Karte des Stapels ist " << myStack.top() << endl;
// Legt ein Element oben auf den Stapel
myStack.push("Karo Ass");
// Ausgabe auf der Konsole ("Karo Ass")
cout << "Die Höhe des Stapels ist " << myStack.size()
<< " und die oberste Karte des Stapels ist " << myStack.top() << endl;
}
Compiler
Zur Übersetzung des Quellcodes einer formalen Sprache nutzen Compiler und Interpreter einen Parser, der einen Stapel verwendet. Der Parser kann z. B. wie ein Kellerautomat arbeiten.
Verarbeitung von Klammerstrukturen
Stapelspeicher eignen sich auch zur Auswertung von Klammerausdrücken, wie sie etwa in der Mathematik geläufig sind. Dabei wird zunächst für Operatoren und Operanden je ein Stapelspeicher initialisiert. Der zu verarbeitende Klammerausdruck wird nun symbolweise eingelesen. Wird eine öffnende Klammer eingelesen, so ist diese zu ignorieren. Wird ein Operand oder Operator eingelesen, so ist dieser auf den jeweiligen Stapelspeicher zu legen.
Wird eine schließende Klammer eingelesen, so wird der oberste Operator vom Stapelspeicher für die Operatoren genommen und entsprechend diesem Operator eine geeignete Anzahl von Operanden, die zur Durchführung der Operation benötigt werden. Das Ergebnis wird dann wieder auf dem Stapelspeicher für Operanden abgelegt. Sobald der Stapelspeicher für die Operatoren leer ist, befindet sich im Stapelspeicher für die Operanden das Ergebnis.
Postfixnotation
Zur Berechnung von Termen wird gelegentlich die Postfixnotation verwendet, die mit Hilfe der Operationen eine Klammersetzung und Prioritätsregeln für die Operationen überflüssig macht. Zahlwerte werden automatisch auf dem Stapel abgelegt. Binäre Operatoren, zum Beispiel +, −, *, /, holen die oberen beiden Werte, unäre Operatoren, zum Beispiel Vorzeichenwechsel, einen Wert vom Stapel und legen anschließend das Zwischenergebnis dort wieder ab.
Infixnotation
Bei der maschinengestützten Auflösung von arithmetischen Ausdrücken in der sogenannten Infixnotation, der Operator steht zwischen den beteiligten Zahlwerten, werden zunächst vorrangige Teilterme in einem Stapel zwischengelagert und so faktisch der Infix-Term schrittweise in einen Postfix-Term umgewandelt, bevor das Ergebnis durch Abarbeiten des Stapels errechnet wird.
Stapelorientierte Sprachen
Stapelorientierte Sprachen, z. B. Forth oder PostScript, wickeln fast alle Variablen-Operationen über einen oder mehrere Stapel ab und stellen neben den oben genannten Operatoren noch weitere zur Verfügung. Beispielsweise tauscht der Forth-Operator swap die obersten beiden Elemente des Stapels. Arithmetische Operationen werden in der Postfix-Notation aufgeschrieben und beeinflussen damit ebenfalls den Stapel.
Forth benutzt einen zweiten Stapel (Return-Stapel) zur Zwischenspeicherung der Rücksprungadressen von Unterprogrammen während der Ausführungsphase. Dieser Stapel wird auch während der Übersetzungsphase für die Adressen der Sprungziele für die Kontrollstrukturen verwendet. Die Übergabe und Rückgabe von Werten an Unterprogrammen geschieht über den ersten Stapel, der zweite nimmt die Rücksprungadresse auf. In den meisten Implementierungen ist zudem ein weiterer Stapel für Gleitkommaoperationen vorgesehen.
Stack-Architektur
Eine Stack-Architektur bezieht sich bei Datenoperationen implizit, also ohne separate Push- und Pop-Befehle, auf einen Stack. Beispiele sind die Intel-FPU (Gleitkommaprozessor) und die Hewlett-Packard-Taschenrechner.
Verwandte Themen
Eine First-In-First-Out-Datenstruktur nennt sich Warteschlange (englisch Queue). Beide Strukturen zeigen ein unterschiedliches Verhalten, haben aber dieselbe Signatur (d. h. Methoden-Struktur), weswegen sie oft zusammen unterrichtet werden.
Eine andere Art Speicher zu verwalten ist die dynamische Speicherverwaltung, die zur Laufzeit entstehende Speicheranforderungen bedienen kann. Dieser Speicher wird oft als Heap bezeichnet und wird eingesetzt, wenn die Lebensdauer der zu speichernden Objekte unterschiedlich ist und nicht dem eingeschränkten Prinzip des Stapelspeichers oder der Warteschlange entspricht.
Siehe auch
Literatur
- Patent DE1094019: Verfahren zur automatischen Verarbeitung von kodierten Daten und Rechenmaschine zur Ausübung des Verfahrens. Angemeldet am 30. März 1957, veröffentlicht am 1. Dezember 1960, Erfinder: Friedrich Ludwig Bauer, Klaus Samelson (Erteilt 12. August 1971).
Weblinks
Einzelnachweise
- Friedrich L. Bauer, Gerhard Goos: Informatik. Eine einführende Übersicht. Erster Teil. 3. Auflage. Springer, Berlin 1982, ISBN 3-540-11722-9, S. 222. „Die Bezeichnung ‚Keller‘ hierfür wurde von Bauer und Samelson in einer deutschen Patentanmeldung vom 30. März 1957 eingeführt.“
- Patent DE1094019: Verfahren zur automatischen Verarbeitung von kodierten Daten und Rechenmaschine zur Ausübung des Verfahrens. Angemeldet am 30. März 1957, veröffentlicht am 1. Dezember 1960, Erfinder: Friedrich Ludwig Bauer, Klaus Samelson.
- GeeksforGeeks: Abstract Data Types
- www.geeksforgeeks.org: Stack Data Structure (Introduction and Program)
- Universität Ulm: Einfacher Stack: in C++ und im C-Stil
- www.geeksforgeeks.org: Stack Class in Java
- Microsoft Docs: stack Class