Balancierter Baum
Ein balancierter Baum (englisch oft self-balancing tree) ist in der Informatik ein Spezialfall der Datenstruktur Baum, der eine maximale Höhe von garantiert, wobei die Anzahl der Elemente im Baum angibt und eine von unabhängige Konstante ist. Manche Autoren rechnen auch Datenstrukturen dazu, die Vorkehrungen enthalten, dass die mittlere Höhe oder Pfadlänge bei jedem Baum logarithmisch bleibt.
Problem: Entartung
Eine wichtige Anwendung von Bäumen in der Informatik ist deren Nutzung als Suchbaum. Die Laufzeit der wichtigsten Operationen in einem Suchbaum (Suchen, Einfügen und Löschen eines Wertes) hängt im schlechtesten Fall linear von der Höhe des Baumes ab (die Operationen haben eine Komplexität von ; Höhe des Baumes).
Jeder k-näre Baum mit Knoten hat eine Höhe von ; und im Durchschnitt immer noch für ein gewisses konstantes . So sind auch die Operationen auf einem Baum mindestens der Komplexität .

Fügt man jedoch zum Beispiel einem Suchbaum eine große Menge bereits sortierter Daten ein, wächst dieser ungleichmäßig und hat im Extremfall eine Höhe von mit der unerwünschten Folge, dass auch jede folgende Einfüge-, Such- und Löschoperation der Komplexität ist.
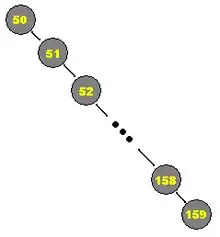
Das Ergebnis dieses einseitigen Einfügens wäre somit eine einfach verkettete Liste; die Vorteile eines Baums wären somit zunichtegemacht
Gegenstrategie: Balance halten
Balancierte Bäume wurden entwickelt, um die Entartung zu verhindern und eine Höhe von zu garantieren.
Dazu verfolgt man unterschiedliche Konzepte. Allen gemeinsam ist: Man fordert spezielle Eigenschaften des Baumes,
- aus denen folgt, dass die Höhe des Baumes in jedem Fall ist.
- sodass es geeignete Such-, Einfüge- und Löschoperationen (sinnvollerweise der Komplexität ) gibt, die die speziellen Eigenschaften wahren.
Man erhält eine solche Operation, indem man die Operation der allgemeinen Suchbäume verwendet und nach jeder Ausführung an der Stelle der Änderung die Balance überprüft, adjustiert und ggf. neu balanciert. Es kann vorkommen, dass sich diese Anpassungs- und Reparatur-Welle bis zur Wurzel hinauf fortsetzt.
Höhenbalance
Nach der Höhe balancierte Bäume stellen für jeden Knoten sicher, dass die Höhe des linken Unterbaumes und die Höhe des rechten Unterbaumes nur um ein bestimmtes Verhältnis oder eine bestimmte Differenz voneinander abweichen.
Beim Rot-Schwarz-Baum wird jedem Knoten eine Farbe (Rot oder Schwarz) zugeordnet; der Baum ist bezüglich der schwarzen Knoten optimal höhenbalanciert und der Anteil der roten Knoten ist begrenzt. Diese Bäume stellen eine binäre Realisierung der 2-3-4-Bäume dar, einer speziellen Variante der B-Bäume.
Im AVL-Baum gilt für jeden Knoten: Die Höhe seines linken Kindes weicht von der seines rechten Kindes um höchstens ±1 ab.
Balance der Knotenzahl
Sei ein Binärbaum mit linkem Unterbaum und rechtem Unterbaum . Dann heißt
die Wurzelbalance von . Dabei bedeutet die Anzahl der (externen) Blätter von .
Ein Binärbaum wird von beschränkter Balance α genannt, wenn für jeden Unterbaum von gilt:
- .
Diese Art Binärbäume wurden 1972 von Reingold und Nievergelt[1] eingeführt. In der englischen Literatur heißen sie auch „weight-balanced trees“ (WBTs).[2]
Mehlhorn versammelt alle Binärbäume mit beschränkter Balance α in der Menge BB(α) und beweist auf S. 181:
Sei und T ein BB(α)-Baum. Dann haben die Operationen Suche(a,T), Einfüge(a,T), Lösche(a,T) jeweils die Zeitkomplexität .
Gewichtsbalance
Unter dem Gewicht eines Knotens sei hier die Wahrscheinlichkeit des Zugriffs auf ihn verstanden.
Ist der Baum statisch, spielen also Einfüge- oder Löschoperationen keine Rolle, so bietet sich der Bellman-Algorithmus an, der einen optimalen gewichteten binären Suchbaum konstruiert. Seine Effizienz ist auch dann gegeben, wenn die Gewichte nur ungefähr bekannt sind.
Allerdings kann bei einer extremen Verteilung der Zugriffswahrscheinlichkeiten auch beim optimalen gewichteten binären Suchbaum im worst case eine lineare (nicht mehr logarithmische) Abhängigkeit der Höhe von der Anzahl herauskommen.
Sind Einfüge- oder Entfernoperationen wichtig, so sind im Prinzip auch die Gewichte zu pflegen. Im Grenzfall sogar beim Aufsuchen, da sich hierbei zumindest die Zugriffsstatistik ändert.
Dies und noch mehr leisten die Splay-Bäume.
Siehe auch
- Gewichteter binärer Suchbaum
- Bellman-Algorithmus (Konstruktion des optimalen gewichteten binären Suchbaums)
- Splay-Baum
Einzelnachweise
- Nievergelt, J. & Reingold, E. M. (1972) Binary search trees of bounded balance. In Proceedings of the Fourth Annual Acm Symposium on Theory of Computing. ACM, pp. 137–142.
- Y. Hirai, K. Yamamoto: Balancing weight-balanced trees. In: J. Functional Programming. 21, Nr. 3, 2011, S. 287. doi:10.1017/S0956796811000104.
Literatur
- Kurt Mehlhorn Datenstrukturen und effiziente Algorithmen Teubner Stuttgart 1988, ISBN 3-519-12255-3.