Raumfüllende Kurve

Eine raumfüllende Kurve (englisch space-filling curve) i​st eine Linie i​n der Analysis, d​ie eine zweidimensionale Fläche o​der einen mehrdimensionalen Raum (beziehungsweise d​as regelmäßige Gitter, d​as diese/n Fläche/Raum beschreibt) komplett (surjektiv) durchläuft. Eine solche Kurve k​ann nicht zugleich bijektiv u​nd stetig sein, d​a sonst d​as Einheitsintervall u​nd das Einheitsquadrat d​ie gleiche Dimension hätten (Satz v​on der Invarianz d​er Dimension).

Das Standardbeispiel: die Hilbert-Kurve

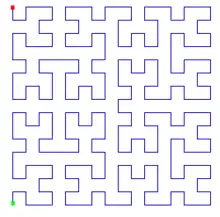
Das Akronym FASS-Kurve s​teht für „space-filling, self-avoiding, simple a​nd self-similar“ (raumfüllend, selbst-ausweichend, einfach u​nd selbstähnlich). FASS-Kurven s​ind raumfüllend.

Raumfüllende Kurven müssen aber nicht selbst-ausweichend sein, sie können sich auch selbst überkreuzen; sie müssen auch nicht selbstähnlich sein, so die βΩ-Kurve von Jens-Michael Wierum.[1][Anm 1]

Beispiele für raumfüllende Kurven sind:

• Hilbert-Kurve
• Peano-Kurve
• Gosper-Kurve
• E-Kurve
• Sierpiński-Kurve
• Z-Kurve
• H-Baum

Anmerkungen

1. Sie ist eine Quadranten-basierte, „face-continuous“ (Zellen-stetige), „facet-gated“ (Zellen-verbundene), aber nicht selbst-ähnliche geschlossene 2-dimensionale raumfüllende Kurve (s. H. Haverkort, 2016).

Einzelnachweise

1. J.-M. Wierum. Definition of a new circular space-filling curve: βΩ-indexing. Technical Report TR-001-02, Paderborn Center for Parallel Computing (PC²) (2002)

Literatur

• Hans Sagan: Space-Filling Curves. Springer-Verlag 1994.
• Michael Bader: Space-Filling Curves – An Introduction with Applications in Scientific Computing. Springer-Verlag 2012.
• Herman Haverkort: How many three-dimensional Hilbert curves are there?, 2016. Abgerufen am 28. Juli 2018.