Binäre Suche

Die binäre Suche ist ein Algorithmus, der auf einem Feld (also meist „in einer Liste“) sehr effizient ein gesuchtes Element findet bzw. eine zuverlässige Aussage über das Fehlen dieses Elementes liefert. Voraussetzung ist, dass die Elemente in dem Feld entsprechend einer totalen Ordnungsrelation angeordnet (sortiert) sind. Der Algorithmus basiert auf einer einfachen Form des Schemas „Teile und Herrsche“, zugleich stellt er auch einen Greedy-Algorithmus dar. Ordnung und spätere Suche müssen sich auf denselben Schlüssel beziehen – beispielsweise kann in einem Telefonbuch, das nach Namen geordnet ist, mit binärer Suche nur nach einem bestimmten Namen gesucht werden, nicht jedoch z. B. nach einer bestimmten Telefonnummer.

Algorithmus

Zuerst wird das mittlere Element des Felds überprüft. Es kann kleiner, größer oder gleich dem Suchwert sein. Ist es kleiner als der gesuchte Wert, muss sich das gesuchte Element in der hinteren Hälfte befinden. Ist das geprüfte mittlere Element hingegen größer, muss nur in der vorderen Hälfte weitergesucht werden. Die jeweils andere Hälfte muss nicht mehr betrachtet werden. Ist es gleich dem Suchwert, dann wurde das gesuchte Element gefunden und die Suche ist beendet.

In der zu untersuchenden Hälfte (und rekursiv in der jeweils verbliebenen Hälfte) wird genauso verfahren: Das mittlere Element liefert wieder die Entscheidung darüber, ob und wo weitergesucht werden muss - davor oder dahinter. Die Länge des Suchbereiches wird so von Schritt zu Schritt halbiert. Spätestens wenn der Suchbereich auf ein einzelnes Element geschrumpft ist, ist die Suche beendet. Dieses eine Element ist entweder das gesuchte Element, oder das gesuchte Element kommt nicht vor; dann ist als Ergebnis bekannt, wohin es einsortiert werden müsste.

Der Algorithmus zur binären Suche wird entweder als Iteration oder Rekursion implementiert. Um ihn verwenden zu können, müssen die Daten bereits sortiert und in einer Datenstruktur vorliegen, in der „direkt“ auf das n-te Element zugegriffen werden kann. Auf einer einfachen verketteten Liste würde die Effizienz verloren gehen (siehe aber Skip-Liste).

Beispiel

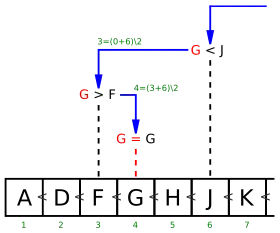
Gesucht ist das Element mit dem Schlüssel G.
(Indizes und Rechnungen in grün;
\ ganzzahlige Division.)

Angenommen, in nebenstehender alphabetisch sortierter Liste von 13 Buchstaben möchte man wissen, ob der Buchstabe G in dieser Liste enthalten ist und an welcher Position er steht oder stehen müsste.

Hierzu prüft man zunächst das mittlere Element der Liste. Mittlere Position ist $13\backslash 2=6$ (' $\backslash$ ' ist Division mit Rest, hier: Teilen und Abrunden), es wird das Element an Position 6 mit dem gesuchten G verglichen. Dort findet man den Wert J. Da im Alphabet G vor J steht (also G kleiner als J ist) und die Liste ja sortiert ist, muss der Suchwert G im Bereich vor Position 6 stehen.

Das macht man nun rekursiv: Man durchsucht nicht den ganzen verbleibenden Bereich, sondern prüft wieder nur das Element in dessen Mitte, hier also das Element an der Position $6\backslash 2=3$ . Dort steht der Wert F. Da G größer als F ist, muss man im Bereich hinter dem F weitersuchen, jedoch vor dem J. Das heißt: man muss im Bereich zwischen Element 3 und Element 6 suchen.

Nun greift man wieder „in die Mitte“ dieses Bereiches zwischen F und J, an Position $({\textit {Position}}(F)+{\textit {Position}}(J))\,\backslash \,2=4$ . Dort finden wir nun das gesuchte Element G.

Wäre stattdessen der Suchwert I gewesen, dann hätten noch der Bereich zwischen G und J geprüft werden müssen. Dort ist H kleiner I; zwischen H und J verbleibt aber kein Bereich mehr, somit ist in dieser Liste kein I enthalten. Als Ergebnis kann der Algorithmus nur liefern, dass I hinter Position 5 einzusortieren wäre.

Die binäre Suche ist effizient: Von den insgesamt 13 Buchstaben mussten wir nur 3 Buchstaben vergleichen, bis wir den gesuchten Buchstaben G gefunden hatten. Auch im schlechtesten Fall hätten wir nur 4 Buchstaben vergleichen müssen.

Ein naiver Algorithmus würde hingegen einfach die ganze Liste von vorne nach hinten durchgehen und müsste somit im ungünstigsten Fall bis zu 13 Elemente untersuchen (wenn der Suchwert Z wäre, das ganz am Ende der Liste steht oder gar nicht in der Liste enthalten ist).

Mit binärer Suche kann man also die Anzahl der benötigten Vergleiche stark verringern. Dieser Vorteil fällt umso stärker ins Gewicht, je größer die zu durchsuchende Liste ist.

Komplexität

Um in einem Feld mit $n$ Einträgen die An- oder Abwesenheit eines Schlüssels festzustellen, werden maximal $\lceil \log _{2}(n+1)\rceil =\lfloor \log _{2}(n)+1\rfloor$ Vergleichsschritte benötigt. Somit hat die binäre Suche in der Landau-Notation ausgedrückt die Zeitkomplexität ${\mathcal {O}}(\log \ n)$ . Damit ist sie deutlich schneller als die lineare Suche, welche allerdings den Vorteil hat, auch in unsortierten Feldern zu funktionieren. In Spezialfällen kann die Interpolationssuche schneller sein als die binäre Suche.

Ähnliche Verfahren und Varianten

Intervallschachtelung

Das hier beschriebene binäre Suchverfahren kann als eine (endliche) Ausprägung der Intervallschachtelung aus der mathematischen Analysis angesehen werden.

Binärer Suchbaum

Der Such-Algorithmus entspricht auch der Suche in einem binären Suchbaum, wenn man das Array als solchen interpretiert: das mittlere Element ist die Wurzel, die Mitten der so entstehenden Hälften die Wurzeln der entsprechenden Teilbäume und so fort. Der aus dieser Interpretation resultierende Binärbaum ist sogar ein sog. vollständig balancierter Binärbaum, also ein Binärbaum, bei dem die Längen der Pfade von den Blättern zur Wurzel sich um höchstens 1 unterscheiden. Das gilt auch unabhängig von der Richtung der Rundung bei der Bildung des Mittelwerts der Indizes.[1] Der so entstandene Binärbaum ist (wie die binäre Suche) unter allen Binärbäumen mit $n$ Elementen optimal in Bezug auf

die maximale Pfadlänge $h:=\lceil \log _{2}(n+1)\rceil$ (= Höhe des Baums),
die Pfadlängensumme, die sich zu $1+(n+1)h-2^{h}$ ergibt, und
die mittlere Pfadlänge.

Letztere entspricht der mittleren Anzahl von Vergleichen, wenn alle Elemente gleich wahrscheinlich sind.

Teilt man nicht in der Mitte, so ist das Ergebnis immer noch ein binärer Suchbaum, jedoch ist er u. U. nicht balanciert und nicht optimal.

Die große Überlegenheit des binären Suchbaums gegenüber der binären Suche im Array liegt erstens im besseren Verhalten bei Einfügungen und Löschungen, bei denen im Mittel ein linearer Aufwand anfällt. Bei Bäumen gibt es auch in diesen Fällen Implementierungen mit garantiert logarithmischer Laufzeit. Dort ist auch die Speicherverwaltung einfacher, da Änderungen nicht das ganze Array betreffen, sondern sich mit dem Entstehen oder Verschwinden eines Elementes direkt verbinden lassen. Zweitens können Bäume besser als das Array an Häufigkeiten angepasst werden. Wenn aber das Array schon fertig sortiert ist und sich dann nicht mehr ändert und Zugriffswahrscheinlichkeiten keine Rolle spielen, ist das Array ein gutes Verfahren.

Binäre Suche und totale Quasiordnung

Da das Array als endlicher Definitionsbereich einer Funktion angesehen werden kann, die natürlich nicht notwendigerweise injektiv sein muss, lässt sich das Vorkommen von Duplikaten leicht über die Funktionswerte regeln. Und wenn die Ordnungsrelation von vornherein schon keine Totalordnung, sondern nur eine totale Quasiordnung ist, ist es ggf. sparsamer, die Äquivalenzklassen vor dem Vergleichen zu bilden, als alle möglichen Duplikate im Array zu halten.

Beispiel

In einer Sammlung von Schlüsselwörtern soll zwar Groß- und Kleinschreibung zulässig sein, die Schlüsselwörter sollen sich aber in ihrer Bedeutung nicht unterscheiden.

Interpolationssuche

Bei der Interpolationssuche wird das Array nicht mittig geteilt, sondern per linearer Interpolation die Position des gesuchten Elementes abgeschätzt. Sind die Schlüssel in etwa äquidistant verteilt, so kann das gesuchte Element in nahezu konstanter Zeit gefunden werden. In einem ungünstigen Fall wird die Laufzeit jedoch linear. Abgesehen davon muss der Definitionsbereich sich für eine lineare Interpolation eignen.

Quadratische Binärsuche

Bei der quadratischen Binärsuche versucht man die Vorteile der Interpolationssuche mit denen der normalen Binärsuche zu kombinieren und mittels Interpolation in jeder Iteration den Suchraum auf ein Intervall der Länge ${\sqrt {n}}$ zu verkleinern.

Verschiedene Implementierungen

In zahlreichen Programmiersprachen ist dieser Algorithmus in den Klassenbibliotheken verfügbar. In Java gibt es beispielsweise java.util.Arrays.binarySearch, in Python das Paket bisect, in C++/STL gibt es std::binary_search in der "algorithms"-Bibliothek.

Als Rückgabewert wird die Feldposition zurückgegeben, an der der gesuchte Eintrag gefunden wurde. Konnte der Eintrag nicht gefunden werden, wird meist die Position zurückgegeben, an der er stehen müsste, jedoch z. B. negativ – als Hinweis auf „wurde nicht gefunden“. Nachfolgende Implementierungen geben jedoch in diesem Fall nur "0" oder "-1" zurück („wurde nicht gefunden“).

Bei großen Feldern kann die Berechnung der Mittenposition

 Variable: Mitte = (Links + Rechts) DIV 2

bei der Addition zu einem Überlauf führen, weshalb oft stattdessen

 Variable: Mitte = Links + ((Rechts - Links) DIV 2)

implementiert wird. Außerdem ist zu beachten, dass der Wert für die Mittenposition 0 erreichen kann und somit der nächste Wert für den rechten Rand negativ wird. Würde man hier einen vorzeichenlosen Datentyp verwenden, fände ein Unterlauf statt und die Bedingung der Schleife würde erfüllt bleiben.

C

Beispiel in C (iterativ):

/**
 * Binäre Suche auf dem Array M nach dem Eintrag suchwert
 *
 * @param M :          zu durchsuchendes Feld
 * @param eintraege :  Anzahl der Feldelemente
 * @param suchwert :   gesuchter Eintrag
 * @return >= 0: Index des gesuchten Eintrags
 *         <  0: nichts gefunden
 */
int binary_search(const int M[], const int eintraege, const int suchwert)
{
    const int NICHT_GEFUNDEN = -1 ;
    int links = 0;                      /* man beginne beim kleinsten Index */
    int rechts = eintraege - 1;         /* Arrays-Index beginnt bei 0 */

    /* Solange die zu durchsuchende Menge nicht leer ist */
    while (links <= rechts)
    {
        int mitte = links + ((rechts - links) / 2); /* Bereich halbieren */

        if (M[mitte] == suchwert)       /* Element suchwert gefunden? */
            return mitte;
        else
            if (M[mitte] > suchwert)
                rechts = mitte - 1;     /* im linken Abschnitt weitersuchen */
            else /* (M[mitte] < suchwert) */
                links = mitte + 1;      /* im rechten Abschnitt weitersuchen */
            /* end if */
        /* end if */
    }

    return NICHT_GEFUNDEN;
    // alternativ: return -links; // (-Returnwert) zeigt auf kleinstes Element >= suchwert: Platz für Einfügen
}

Python

Rekursives Verfahren in Python:

 def binaersuche_rekursiv(werte, gesucht, start, ende):
    if ende < start:
        return 'nicht gefunden'
        # alternativ: return -start # bei (-Returnwert) waere die richtige Einfuege-Position
    # end if
    mitte = (start + ende) // 2
    if werte[mitte] == gesucht:
        return mitte
    elif werte[mitte] < gesucht:
        return binaersuche_rekursiv(werte, gesucht, mitte + 1, ende)
    else:
        return binaersuche_rekursiv(werte, gesucht, start, mitte - 1)
    # end if
 # end function

 def binaersuche(werte, gesucht):
    return binaersuche_rekursiv(werte, gesucht, 0, len(werte) - 1)
 # end function

Haskell

Beispiel in der funktionalen Programmiersprache Haskell (rekursiv)

data SearchResult = NotFound Integer | Found Integer deriving (Eq, Ord, Show)

bsearch :: Ord a => a               -- hiernach wird gesucht
                 -> (Integer -> a)  -- zu durchsuchende Folge, monoton
                 -> Integer         -- Indexuntergrenze (einschließlich)
                 -> Integer         -- Indexobergrenze (ausschließlich)
                 -> SearchResult
bsearch dest s lo hi
    | s lo > dest = NotFound lo
    | hi <= lo    = NotFound lo
    | otherwise   = go lo hi
    where
        -- Invarianten: lo < hi, lo ist immer klein genug, hi ist immer zu groß.
        -- Wir suchen den *größten* Index, der klein genug ist.
        go lo hi
            | lo + 1 == hi = if s lo == dest then Found lo else NotFound hi
            | dest < s mid = go lo mid
            | otherwise    = go mid hi
            where mid = (lo+hi)`div`2

Anmerkungen

Bei einer Belegung des Feldes mit $n=2^{h}-1$ Einträgen (das entspricht einem vollständigen Binärbaum der Höhe $h$ ) haben alle Halbierungen einen Divisionsrest von 0.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Bei einer Belegung des Feldes mit $n=2^{h}-1$ Einträgen (das entspricht einem vollständigen Binärbaum der Höhe $h$ ) haben alle Halbierungen einen Divisionsrest von 0.