Methode der kleinen Schritte
Die Methode der kleinen Schritte ist eine physikalische Anwendung des eulerschen Polygonzugverfahrens, die zur näherungsweisen mathematischen Beschreibung von Bewegungen dient.
 |
Dieser Artikel wurde auf der Qualitätssicherungsseite des Portals Mathematik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Mathematik auf ein akzeptables Niveau zu bringen.
Bitte hilf mit, die Mängel dieses Artikels zu beseitigen, und beteilige dich bitte an der Diskussion! (Artikel eintragen) |
Wenn beispielsweise die wirkende Kraft nicht konstant ist, so ist Auswertung des zweiten newtonschen Gesetzes mit einfacher Schul-Mathematik oft nicht möglich, da die Beschleunigung nicht konstant ist. Auf einfachstem Niveau wird die Beschleunigung jeweils für ein Zeitintervall Δt als konstant angenommen, daraus die resultierende Geschwindigkeit und der Ort am Ende des Zeitabschnittes bestimmt und mit der nun wirkenden Kraft der nächste Berechnungsschritt im nächsten Zeitintervall Δt vorgenommen.
Anwendungsbeispiel: Erdnaher freier Fall
Man wendet die Methode der kleinen Schritte beispielsweise bei der Bewegung eines Fallschirmspringers (im Fall) mit Luftwiderstand an.
Physikalischer Hintergrund
- Beim freien Fall in Erdnähe würde die Geschwindigkeit eines fallenden Körpers – bei Vernachlässigung des Luftwiderstandes – um 9,81 m/s pro Sekunde steigen. Dann wäre der freie Fall eine gleichmäßig beschleunigte Bewegung. Ein Fallschirmspringer, der sich aus einem stationären Ballon fallen lässt, wird zunächst immer schneller, seine Geschwindigkeit nimmt stetig zu. Seine Beschleunigung entspricht dabei der Fallbeschleunigung g=9,81 m/s² in der Nähe der Erdoberfläche und ist größer als die eines Autos: Nach einer Sekunde hat er theoretisch eine Geschwindigkeit von v = 9,81 m/s (ca. 35 km/h), nach zwei Sekunden 19,62 m/s (ca. 71 km/h), nach drei Sekunden 29,43 m/s (ca. 106 km/h). In einem echten freien Fall, d. h. im Vakuum, würde die Geschwindigkeit linear weiter entsprechend ansteigen.
- Tatsächlich wirkt auf den Fallschirmspringer jedoch auch der Luftwiderstand, welcher quadratisch mit der Geschwindigkeit zunimmt. Die resultierende Beschleunigung entspricht daher nur am Anfang der Erdbeschleunigung, danach nimmt sie ab, bis sie nach wenigen Sekunden null wird – der Fallschirmspringer fällt ab diesem Zeitpunkt (je nach Wahl der Anfangsbedingungen) mit seiner Fallgrenzgeschwindigkeit von z. B. ca. 55 m/s (ca. 198 km/h).
Anwendung einer Tabellenkalkulation
Mit Hilfe einer Tabellenkalkulation kann man derartige Probleme aber in viele einfache und vor allem lösbare Teilaufgaben zerlegen, deren Ergebnisse man durch das Computerprogramm zur Gesamtlösung zusammensetzen lässt. Die Vorteile liegen auf der Hand:
- Man benötigt keine Kenntnisse in höherer Mathematik
- Die Integration wird durch Summieren ersetzt. Das Ergebnis ist zwar nicht exakt, genügt aber den meisten praktischen Anforderungen.
- Anhand von Zwischenergebnissen erkennt man sofort kleine Irrtümer, die sich korrigieren lassen.
- Die vielen überprüfbaren Zwischenergebnisse steigern das Vertrauen in das Resultat.
- Durch Hinzufügen weiterer relevanter Formeln kann die Lösung schrittweise der Realität angepasst werden.
Die Vorgehensweise ist immer gleich: Mit elementaren Formeln werden relevante Größen wie Kraft, Beschleunigung oder Temperatur für einen gewissen Zeitpunkt berechnet – das sind die Anfangswerte für den nächsten Zeitpunkt. Die Ergebnisse sind nur dann korrekt, wenn sich von einem Zeitpunkt zum nächsten nur wenig ändert. Wie groß diese Änderungen und vor allem jeder Zeitschritt sein dürfen, kann man den Ergebnissen leicht entnehmen. Komplexe Formeln, wie sie beispielsweise bei der Wettervorhersage vorkommen, lassen sich gar nicht anders auswerten.
Einzelformeln des freien Falls mit Luftwiderstand
In der folgenden Berechnung wird angenommen, dass ein kugelförmiger Eisen-Meteor der Masse m = 4 g und der Querschnittsfläche A = 1 cm² mit der Geschwindigkeit v = 15 km/s in die Atmosphäre eindringt und abgebremst wird. Gesucht sind Geschwindigkeit und Bremsverzögerung als Funktion der Höhe. Diese Werte werden in bekannte Formeln eingesetzt und für jeden Zeitschritt neu berechnet. Die Einzelergebnisse werden in der Tabelle zu den gesuchten Größen kombiniert und zum Schluss graphisch ausgegeben. Man startet das Verfahren in ausreichend großer Höhe h, wo der Luftwiderstand noch vernachlässigbar ist.
- Die Gravitationsbeschleunigung der Erde wird mit zunehmendem Abstand h über der Erdoberfläche kleiner. Dafür gilt
- In dieser Höhe h beträgt die Dichte der Luft nur noch (Barometrische Höhenformel)
- Der Strömungswiderstand in Luft FLuft bei der Geschwindigkeit v hängt auch von dieser Dichte ab
- Bei Flugrichtung zum Erdmittelpunkt ist die effektive Beschleunigung auf den Meteor der Masse m die Differenz von Gravitationsbeschleunigung und Bremsbeschleunigung
- Mit diesem Zwischenergebnis lässt sich einen Zeitschritt dt später die dann gültige Geschwindigkeit errechnen
- und daraus der Ort, an dem sich der Meteor dann befindet. Damit startet ein neuer Zyklus.
Die Berechnung erfolgt schrittweise mit elementaren Mitteln und entspricht einer einfachen Integration, die bei ausreichend kleinem dt brauchbare Ergebnisse liefert. Speziell für die letzten beiden Schritte existieren bessere, aber auch aufwendigere Verfahren, die in Numerische Integration beschrieben sind. Oft ist deren Anwendung übertrieben, wenn nur ein schneller Überblick gewünscht wird oder – wie in diesem Beispiel – die Formel für den Strömungswiderstand für Überschallgeschwindigkeit nicht exakt gilt.
Numerische Lösung
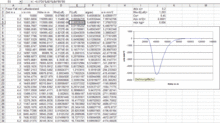
Zunächst werden die Parameter in den Zellen J1 bis J5 und die Startwerte in A3, B3, C3 festgelegt, diese Werte werden fast überall in der Tabelle benötigt. In anderen Programmiersprachen würde man von „globalen Variablen“ sprechen. Die eben aufgezählten Formeln werden in benachbarten Spalten der Tabellenkalkulation programmiert, die Zwischenergebnisse werden im Regelfall in weiter rechts liegenden Spalten weiterverarbeitet. Die „Weiterschaltung“ in die folgende Zeile erfolgt dadurch, dass das Ergebnis der Zelle G3 verwendet wird, um den Inhalt der Zelle B4 nach dem folgenden Zeitschritt zu berechnen. Zum Schluss kopiert man die Formeln der 3. bzw. 4. Zeile in die nächsten 2000 Zeilen – gleichzeitig wird das Ergebnis berechnet.
Von ausschlaggebender Wichtigkeit für die physikalische Korrektheit der Ergebnisse ist die sinnvolle Wahl des Zeitschrittes dt, der möglichst klein sein soll und in der nebenstehenden Tabelle den – für diese Aufgabenstellung – recht hohen Wert 0,2 s hat. Das führt in der Umgebung der Zelle G20 zu gerade noch akzeptierbaren Wertesprüngen von etwa 40 %. Allerdings bewirkt auch eine Vergrößerung auf dt = 1 s noch keine gravierenden Änderungen, was die Robustheit dieses Lösungsverfahrens demonstriert.
Im nebenstehenden Bild wird neben der Tabelle die Gesamtbeschleunigung in Abhängigkeit von der Höhe dargestellt. Die überraschenden Ergebnisse:
- Die Meteore werden fast unabhängig von ihrer Masse in etwa 40 km Höhe am stärksten gebremst und können dabei in Bruchstücke zerlegt werden oder verglühen.
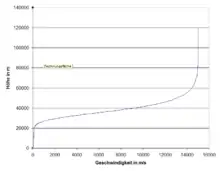
- Die Geschwindigkeiten in den letzten Kilometern über der Erdoberfläche betragen stets etwa 40 m/s – wenn die Bruchstücke bis dahin nicht verglüht sind. Der berechnete Geschwindigkeitsverlauf ist im unteren Bild dargestellt.
Weiterführende Untersuchungen
Das beschriebene Verfahren lädt dazu ein, Parameter wie Größe und Anfangsgeschwindigkeit zu variieren und deren Auswirkungen auf die berechneten Ergebnisse zu untersuchen. Diese Art von „experimenteller Mathematik“ kann zu größerem Verständnis der enthaltenen Physik führen als die Auswertung der komplexen Formeln im vorhergehenden Absatz.