Irregulärer Satellit
Irreguläre Satelliten, auch irreguläre Monde genannt, sind Monde, deren Bahnen größere Inklinationen, Exzentrizitäten und Entfernungen zu ihren Planeten aufweisen als reguläre Satelliten. Heute sind im Sonnensystem über 100 irreguläre Monde bekannt.[1]

Entdeckungen
Vor dem Jahr 1997, in dem die irregulären Uranusmonde Caliban und Sycorax entdeckt wurden, waren inklusive Triton nur elf irreguläre Monde bekannt. Um die Jahrtausendwende begann durch die höhere Lichtempfindlichkeit der aufkommenden großflächigen CCD-Sensoren eine rasante Serie an Entdeckungen.[2]
Definition
Die Monde der Planeten des Sonnensystems weisen hinsichtlich ihrer Bahneigenschaften eine natürliche Aufteilung auf:
- reguläre Monde umkreisen ihren Planeten auf engen, nahezu kreisförmigen Bahnen (Exzentrizitäten von etwa 0,01) mit niedrigen Inklinationen von wenigen Grad. Sie umlaufen ihren Planeten grundsätzlich prograd, also in derselben Richtung, in welcher der Planet die Sonne umkreist.[2]
- irreguläre Monde hingegen kreisen auf wesentlich weiteren Bahnen mit großen Exzentrizitäten (0,1 bis 0,7) und scheinbar zufällig verteilten Inklinationen von bis zu 180°.[2]
Um die Entfernungen der Bahnen von ihrem Planeten planetenübergreifend vergleichen zu können, gibt man die Entfernungen in Vielfachen des Hill-Radius rH an; dieser ist diejenige Entfernung, bis zu welcher die Gravitationskraft des Planeten über die der Sonne dominiert:
- reguläre Satelliten findet man auf Bahnen mit großen Halbachsen unter 0,05 rH,
- irreguläre Satelliten haben Entfernungen bis etwa 0,5 rH, was etwa der maximal möglichen Entfernung entspricht, die ein Mond haben kann.[3]
Eine alternative, quantitativere Abgrenzung definierte beispielsweise Burns 1986 über die Präzession der Bahnen:
- danach ist ein Mond ein irregulärer Mond, wenn die Präzession seines Orbits überwiegend durch die Sonne und nicht mehr vom Planeten verursacht wird.[4]
Durch die starke Dichotomie der Mondorbitale unterscheiden sich die o. g. Definitionen in der Klassifikation der bekannten Monde üblicherweise nicht. Einzige Ausnahme ist hier Neptuns Mond Triton, welcher eine Sonderrolle einnimmt (siehe unten).
Eigenschaften
Irreguläre Monde wurden um alle vier Riesenplaneten Jupiter, Saturn, Uranus und Neptun gefunden.
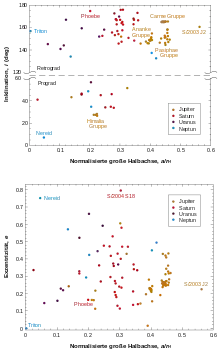
Betrachtet man die Bahneigenschaften der irregulären Monde wie in der nebenstehenden Abbildung, so sieht man einige ihrer Eigenschaften:
- Die Exzentrizitäten, Inklinationen und auf rH normierten Entfernungen sind fast über den gesamten Bereich möglicher Werte breit gestreut. Es gibt jedoch Gruppen irregulärer Monde, welche äußerst ähnliche Bahnen haben. Man vermutet, dass diese durch Kollisionen zweier irregulärer Monde entstanden sind.[2] Diese Vermutung wird dadurch unterstützt, dass die Farben von Monden, deren Bahnen eine Gruppe bilden, untereinander sehr ähnlich sind.[2]
- Die auf die Hillsphäre normierten Entfernungen nehmen von Planet zu Planet mit steigender Sonnenentfernung ab.[2] Der Grund dafür ist noch unbekannt, eine mögliche Erklärung könnten Kollisionen von irregulären Planeten sein.
- Prograde irreguläre Monde gibt es nur bis zu einer Entfernung von etwa 0,35 rH, während retrograde Monde auch weiter außen gefunden werden.[2] Dies kann damit erklärt werden, dass das Stabilitätslimit der Umlaufbahnen – also die Distanz, bis zu welcher ein Mond überhaupt theoretisch eine stabile Umlaufbahn besitzen kann – für prograde Monde bei 0,53 rH und bei retrograden Monden bei 0,69 rH liegt.[3]
- Während ausnahmslos alle regulären Planeten prograde Bahnen haben, haben bei allen Planeten die meisten irregulären Monde retrograde Bahnen: das Verhältnis von retrograden zu prograden Satelliten beträgt etwa 4,5:1.[2] Da die meisten Entstehungsmodelle irregulärer Planeten (s. u.) eine symmetrische Verteilung auf pro- und retrograde Bahnen vorhersagen, geht man davon aus, dass einige besonders große Monde auf retrograden Bahnen mehrere Monde auf prograden Orbits zerstörten, oder die Asymmetrie durch die höhere Stabilität von Monden auf irregulären Bahnen verursacht wird.[2][5]
Die Farben der irregulären Monde reichen von neutral bis rötlich.[2] Die Farbfeinverteilung der Monde der unterschiedlichen Planeten unterscheidet sich nicht, was dafür spricht, dass die Monde nicht um den Planeten entstanden sind, sondern einen gemeinsamen Ursprung haben.[2]
Die Größen der meisten irregulären Monde konnte bisher nur ungenau bestimmt werden. Die Radien der bisher bekannten irregulären Monde betragen zwischen wenigen Kilometern und etwa 106 Kilometer (Phoebe), wobei es möglich ist, dass noch kleinere Monde unter Umständen nur noch nicht gefunden wurden. Ebenfalls auf die Verzerrung durch die Beobachtungsmöglichkeiten zurückzuführen ist, dass man von den näheren Planeten mehr und kleinere irreguläre Monde kennt.
Die Anzahl der Monde, deren Durchmesser kleiner oder gleich einem bestimmten Durchmesser ist (englisch size-frequency distribution, kurz SFD), kann, wie bei den meisten Objekten im Sonnensystem, durch zwei Potenzfunktionen beschrieben werden. Dabei beträgt der Exponent für kleine Monde (d. h. mit Radien kleiner 10 km) etwa 3,5 und für Objekte mit Radien größer als 10 Kilometer etwa 2.
.jpg.webp)
Triton
Der Neptunmond Triton spielt eine Sonderrolle. Er wird oft zu den regulären Monden gezählt, da er eine für reguläre Monden übliche enge Umlaufbahn (0,003 rH) mit geringer Exzentrizität (0,00002) und einen für irreguläre Monde ungewöhnlich großen Radius (2706 ± 2 km) hat. Allerdings umläuft er Neptun auf einer retrograden Bahn (Inklination von 156,8°), und muss deshalb ebenfalls eingefangen worden sein.
Entstehungsmodelle
Während sich reguläre Satelliten nach heutigem Wissenstand durch Akkretion aus der planetaren Gasscheibe gebildet haben, können irreguläre Monde aus mehreren Gründen nicht auf diese Weise entstehen:
- sie sind von den regulären Monden räumlich zu stark getrennt, um aus derselben Gasscheibe entstanden zu sein,
- per Akkretion können keine derartig großen Exzentrizitäten entstehen,
- vor allem können aus einer Gasscheibe keine retrograd umlaufenden Monde entstehen.[5]
Die Herkunft der irregulären Monde ist daher noch ungeklärt. Sie müssen auf irgendeine Art vom Planeten aus einem heliozentrischen Orbit eingefangen worden sein. Das System Sonne-Planet-einzufangender Körper reicht jedoch nicht aus, da es reversibel in der Zeit ist und somit jeder Weg des Körpers von der Umlaufbahn um die Sonne zu einer Bahn um den Planeten auch wieder ein möglicher Weg zurück ist.[5]
Gas drag
Als eine mögliche Erklärung, um die zeitliche Reversibilität zu brechen, wurde vorgeschlagen, dass der Körper Energie durch Reibung (engl. drag) an das den Planeten umgebende Gas verliert.
Dieses Modell kann zwar einige der irregulären Monde von Jupiter erklären, nicht jedoch alle, da einige weiter entfernt sind als die Gasscheibe gereicht hat. Auch auf die irregulären Monde von Neptun und Uranus lässt sich dieses Modell vermutlich nicht anwenden, da deren Gasscheiben sich vermutlich nicht für dieses Modell eignen.[6][5]
Migrationsmodelle wie das Nizza-Modell (s. u.) führen zu einem weiteren großen Problem für Gas-Drag-Modelle: kommt den so entstandenen irregulären Monden ein großes Planetesimal oder ein Planet zu nahe, werden sie äußerst effizient wieder aus dem System des Planeten gefegt.[5] Wurde dies früher als Argument gegen Modelle, in welchen sich Planeten nahe kommen, genannt, so wird es spätestens seit den Erfolgen des Nizza-Modells meist als Argument gegen die Gas-Drag-Modelle gewertet.
Ein weiteres Problem der Gas-Drag-Modelle sind die Farben der irregulären Monde: würden die Monde aus der lokalen Umgebung der Planeten stammen, so müssten alle Monde eines Planeten eine ähnliche Farbe haben, und diese Farben müssten vom Sonnenabstand des Planeten abhängen.
Nizza-Modell
Das Nizza-Modell geht davon aus, dass kurz nach der Auflösung der protoplanetaren Gasscheibe, aus welcher die Riesenplaneten entstanden sind, ausgelöst durch Wechselwirkung der Planeten mit einer damals das Sonnensystem umgebenden massiven Scheibe von Planetesimalen eine Resonanz zwischen den Bahnen von Jupiter und Saturn auftritt. Diese destabilisiert das System, bevor es sich nach etwa hundert Millionen Jahren wieder stabilisiert. In der chaotischen Phase kommen sich Planeten immer wieder nahe, und zeitgleich fliegen zahlreiche Planetesimale durch das Sonnensystem.
Im Rahmen des Nizza-Modells erklärten Nesvorný und Kollegen den Einfang von irregulären Monden über Drei-Körper-Reaktionen: Zwei Planeten kommen sich so nahe, dass sie gegenseitig in den Hillradius des anderen eindringen, einige der ebenfalls durch den Hillradius der Planeten fliegenden Planetesimale werden dadurch auf weit entfernten Bahnen um einen der Planeten eingefangen und kreisen nun als irreguläre Monde um den Planeten.
In den Simulationen von Nesvorný und Kollegen erzeugt das Nizza-Modell deutlich zu viele irreguläre Planeten, und auch die Größenverteilung (SFD) passt nicht sehr gut mit den Beobachtungen überein. Die Erklärung dafür liegt darin, dass es durch die chaotischen Bahnen der irregulären Mode zu zahlreichen Kollisionen kam, in welchen viele Monde zerstört wurden. Simulationen, die dies berücksichtigen, können die irregulären Monde aller vier Riesenplaneten erfolgreich erklären.[7]
Weblinks
Einzelnachweise
- Philip D. Nicholson, Matija Cuk, Scott S. Sheppard, David Nesvorny, Torrence V. Johnson: Irregular satellites of the giant planets. In: M. Antonietta Barucci (Hrsg.): The Solar System Beyond Neptune. 1, 2008, S. 411–424.
- David Jewitt, Nader Haghighipour: Irregular Satellites of the Planets: Products of Capture in the Early Solar System. In: Annual Review of Astronomy and Astrophysics. 45, Nr. 1, 2007, S. 261–295, doi:10.1146/annurev.astro.44.051905.092459.
- Douglas P. Hamilton, Alexander V. Krivov: Dynamics of Distant Moons of Asteroids. In: Icarus. 128, Nr. 1, 1997, S. 241–249, doi:10.1006/icar.1997.5738.
- Joseph A. Burns: The evolution of satellite orbits. In: Satellites. Vol. 1, 1986.
- David Nesvorný, David Vokrouhlický, Alessandro Morbidelli: Capture of Irregular Satellites during Planetary Encounters. In: The Astronomical Journal. 133, Nr. 5, 2007, S. 1962–1976, doi:10.1086/512850.
- J. Pollack: Formation of the Giant Planets by Concurrent Accretion of Solids and Gas. In: Icarus. 124, 1996, S. 62–85. ISSN 0019-1035
- William F. Bottke, David Nesvorný, David Vokrouhlický, Alessandro Morbidelli: The Irregular Satellites: The Most Collisionally Evolved Populations in the Solar System. In: The Astronomical Journal. 139, Nr. 3, 2010, S. 994–1014, doi:10.1088/0004-6256/139/3/994.