Geoid
Das Geoid ist eine wichtige Bezugsfläche im Schwerefeld der Erde. Es dient zur Definition von Höhen sowie zur Vermessung und Beschreibung der Erdfigur.[1] In guter Näherung wird das Geoid durch den mittleren Meeresspiegel der Weltmeere repräsentiert und ist damit außerhalb der Landmassen direkt in seiner Form sichtbar.
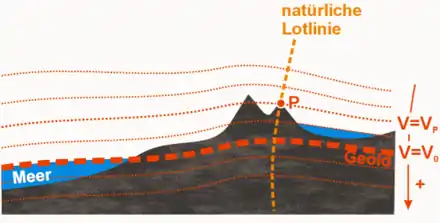
Die Oberflächen des Geoids sind definiert als die Flächen gleichen Schwerepotentials. Damit ist die Geoidoberfläche auf Meereshöhe die aufschlussreichste, jedoch sind alle anderen beliebigen Oberflächen gleichbedeutend. Die natürliche Lotrichtung und die Geoidoberflächen stehen also in jedem Punkt senkrecht zueinander. Daher kann das Geoid durch Messung der Erdbeschleunigung bestimmt werden. Zwei beliebige Punkte auf dem Geoid haben das gleiche Schwerepotential und deshalb die gleiche dynamische Höhe.
Im Gegensatz zum Schwerepotential ist die Schwerebeschleunigung g auf dem Geoid nicht konstant. Sie sinkt aufgrund der vom Pol zum Äquator ansteigenden Zentrifugalbeschleunigung vom Pol zum Äquator von 9,83 auf 9,78 m/s².[2] Zudem variiert sie lokal aufgrund der inhomogenen Masseverteilung der Erde.
Das Geoid ist ein physikalisches Modell der Erdfigur, das 1828 von Carl Friedrich Gauß beschrieben wurde – im Gegensatz zum geometrischen Modell des Erdellipsoids. Die Bezeichnung Geoid geht auf Johann Benedict Listing zurück, der es 1871 als Fläche gleichen Schwerepotentials beschrieb: Das Geoid ist die Äquipotentialfläche des Schwerefelds der Erde auf dem Niveau des mittleren Meeresspiegels, also aller Punkte, die dasselbe Geopotential besitzen, zusammengesetzt aus dem Gravitationspotential sowie dem Zentrifugalpotential an dem betreffenden Ort.
Erdfigur und Geoid
Der Meeresspiegel ist – abgesehen von Strömungen und Gezeiten – eine sogenannte Niveaufläche, auf der das Schwerepotential konstant ist, weil sie überall senkrecht auf der Lotrichtung steht. Zwar gibt es unendlich viele solcher Äquipotentialflächen, die wie Zwiebelschalen um den Erdmittelpunkt verlaufen. Der Meeresspiegel hat jedoch die Besonderheit, dass er erdumspannend durch Pegelbeobachtung zu beobachten ist und sich daher als weltweite Bezugsfläche für Höhenmessungen und Schweremessungen eignet. Zu diesem Zweck haben einige europäische Länder schon vor etwa 200 Jahren Pegel an verschiedenen Küstenorten eingerichtet und vermessen, beispielsweise den Amsterdamer Pegel oder die Pegelstationen in Triest, Genua, Marseille und St. Petersburg. Ihre durch Höhennetze mögliche Verbindung über Land hätte sich zur Bestimmung des kontinentalen Geoids geeignet, was aber aus politischen Gründen erst mit den Europanetzen des 20. Jahrhunderts erfolgte.
Die regionale Bestimmung der Geoidfläche erfolgte anfangs durch astrogeodätische Bestimmung der Lotrichtung auf einzelnen Vermessungspunkten und ab den 1930er-Jahren durch profil- oder rasterartig angelegte Schweremessungen mit Gravimetern. Von den Ämtern der Landesvermessung wurden die Astrogeoide und die gravimetrische Geoidbestimmung seit etwa 1970 durch starke Verdichtung der Lotabweichungs- bzw. Schwerenetze merklich verbessert, während die globale Genauigkeit durch jahrelange Satellitenaltimetrie der Meeresoberfläche gesteigert wurde.
Es dominieren die automatisierten Verfahren der Satellitengeodäsie die Bestimmung des Erdschwerefeldes. Sie zeigen das Geoid als eine unregelmäßige Fläche mit vielen Beulen und Dellen, die aber nur etwa 0,001 Prozent des Erdradius ausmachen. Diese wellenartigen Geoidformen werden durch Schwereanomalien der Gebirge und ungleichmäßige Massenverteilung im Erdinnern verursacht.
Wegen seiner unregelmäßigen Form ist das Geoid mathematisch sehr schwer zu beschreiben, wogegen die praktische Landesvermessung, die Kartografie und die GPS-Ortsbestimmung eine einfacher definierte Erdfigur benötigen. Solche Bezugsflächen für Berechnungen und Kartenabbildungen sind meist Rotationsellipsoide, die das Geoid auf etwa 50 m genau approximieren. Diese streng mathematischen Flächen können aber nicht direkt durch Messen physikalischer Größen bestimmt werden.
Deshalb muss für die praktische Handhabung die Abweichung zwischen der physikalischen Erdfigur (Geoid) und ihrem mathematischen, für Berechnungen geeigneten Pendant (Rotationsellipsoid) durch systematische Messungen bestimmt werden. Die Abweichungen des Geoids von einem Referenzellipsoid (z. B. WGS84, GRS 80, Internationales Ellipsoid 1924) werden als Geoidundulation bzw. Geoidhöhe bezeichnet und können bis 100 m ausmachen und variieren auf 1000 km um etwa ±30 m:
- Geoidundulation , mit ellipsoidischer (geometrischer) Höhe und orthometrischer (physikalischer) Höhe
Geoid-Näherungen mit Kugelfunktionen
In nullter Näherung ist das Geoid unter Vernachlässigung des Potentials der Zentrifugalkraft Uz eine Äquipotentialfläche im Gravitationsfeld eines Massepunktes: U(r) = G·M/r + Uz (G: Gravitationskonstante, M: Masse der Erde, r: Abstand vom Mittelpunkt der Erde). Für viele Rechnungen in Himmelsmechanik und Raumfahrt liefert diese Vereinfachung brauchbare Ergebnisse. Das Geoid ist eine Kugel mit einem Parameter R ≈ 6373 km für den Radius.
Abweichungen von der Kugelform lassen sich durch Legendre-Polynome Pn(cos(θ)) beschreiben (θ: Breitenwinkel, R: mittlerer Erdradius, Jn: Entwicklungskoeffizienten):
mit den Koeffizienten:
- J0 = 1; Kugelnäherung
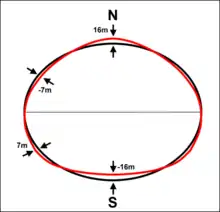
- J1 = 0; kein Dipolmoment, Nord- und Südhalbkugel gleich schwer
- J2 = 1082,6·10−6; genäherte Erdfigur als Rotationsellipsoid mit gleich großen Äquator-Halbachsen a = b ≈ 6378 km und c ≈ 6357 km als Polarachse. J2 berücksichtigt die sogenannte Massefunktion zweiter Ordnung, die von der Erdabplattung herrührt
- J3 = 2,51·10−6; Aufsetzen einer birnenähnlichen Struktur auf das Ellipsoid (siehe Zeichnung)
- J4 = 1,60·10−6
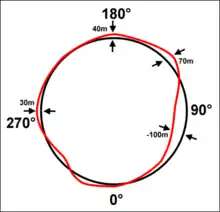
Die Massefunktionen J3 und J4 bewirken geometrische Abweichungen vom mittleren Erdellipsoid, die weniger als 20 m betragen. Die starke Überhöhung in der Zeichnung rechts veranschaulicht, warum die Erde manchmal als "birnenförmig" beschrieben wird.
Eine verbesserte Näherung führt weitere Kugelfunktions-Koeffizienten ein, die einige Abhängigkeiten des Geoids von der geografischen Länge berücksichtigen. Die Schemazeichnung rechts macht deutlich, dass Schwereabweichungen im Längengrad vorliegen, die einem Höhenunterschied von 170 m entsprechen. Sie sind die Ursache dafür, dass es für geostationäre Satelliten nur zwei stabile und zwei labile Bahnpositionen gibt.
Geoidbestimmung
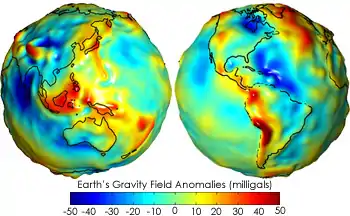

Die bisher genaueste Bestimmung des gesamten Geoids erfolgte durch das Projekt GRACE. Es besteht aus zwei Satelliten die mit etwa 200 km Abstand in gleicher Höhe die Erde umkreisen. Der Abstand der beiden Satelliten wird ständig mit hoher Genauigkeit vermessen. Aus der Änderung dieses Abstands schließt man dann auf die Form des Geoids.
Die Geoidbestimmung kann außerdem mit Methoden der Astrogeodäsie oder gravimetrisch erfolgen; beide liefern die Detailformen des Geoids genauer als die Satelliten, sind aber aufwendiger. Die Bestimmung des Astrogeoids (Messung der Lotabweichung) wurde schon vor 100 Jahren erprobt und ist das genaueste Verfahren, erfordert aber ein Vermessungsnetz und klare Nächte zur Sternbeobachtung. Das dafür optimale Instrument der Astrogeodäsie ist die Zenitkamera: mit ihrer Hilfe kann durch CCD-Aufnahmen des zenitalen Sternfeldes die Lotrichtung in einem Messpunkt hochgenau und teilweise automatisiert bestimmt werden. Diese Lotrichtungen beziehen sich auf das Schwerefeld und damit auf das Geoid. Um aus Lotabweichungen die Neigung des Geoids gegenüber dem Referenzellipsoid zu bestimmen, ist die Kenntnis der ellipsoidischen Koordinaten des Messpunktes erforderlich. Diese können aus der Landesvermessung oder mit GNSS-Navigationssatelliten bestimmt werden.
Bei der Gravimetrie wird das Geoid durch rasterförmige Messung der Erdbeschleunigung bestimmt. Für eine globale Geoidbestimmung durch hinreichend dichte Verteilung der Messpunkte ist das Verfahren allerdings zu aufwändig. Zur Geoid-Interpolation zwischen den Messpunkten ist im Gebirge – ebenso wie beim Astrogeoid – ein digitales Geländemodell vorteilhaft.
Im Juni 2011 veröffentlichte das Deutsche GeoForschungsZentrum (GFZ) in Potsdam das als Potsdamer Kartoffel bekanntgewordene Schweremodell „EIGEN-6C“.[3][4][5] Dieses globale Modell wurde aus den kombinierten Daten verschiedener Sat-Messungen von LAGEOS, GRACE, GOCE und anderen Messmethoden erstellt und hat eine räumliche Auflösung von ca. 12 km.
Ursachen der Geoidundulationen
Dichteanomalien im Erdmantel aufgrund von Mantelkonvektion und mit ihnen verbundenen Topografievariationen sind die Ursache für den Hauptteil der beobachteten Geoid-Undulationen.
Die Ursachen für die langwelligen Geoidschwankungen (Geoidundulationen) liegen in großräumigen Dichtevariationen im Erdmantel und zu geringerem Maße auch in der Erdkruste. Eine anomal höhere Gesteinsdichte erzeugt eine zusätzliche Gravitationsbeschleunigung und beult somit das Geoid aus, geringere Dichten führen zu „Dellen“ im Geoid. Aber auch die Topografie selbst stellt eine lateral variable Massenvariation dar (→ Hebung (Geologie)) und führt zu Undulationen. Die Ursache für Dichtevariationen im Erdmantel liegt in der Mantelkonvektion: Heiße Mantelregionen sind weniger dicht und steigen auf (→ Plume (Geologie)); kalte, dichte Regionen sinken ab.
Man würde nun also über aufsteigenden Konvektionsströmen „Dellen“ im Geoid erwarten, über abtauchenden Konvektionsströmen (z. B. über Subduktionszonen) „Beulen“, was für den Westpazifik im Großen und Ganzen tatsächlich mit den Beobachtungen übereinstimmt. Die Sache wird jedoch dadurch komplizierter, dass aufsteigende Konvektionsströme die Erdoberfläche selbst anheben können (Bsp.: Island, Hawaii). Die so erzeugte Topografie bezeichnet man als „dynamische Topografie“. Hierdurch wird die eigentliche negative Geoid-Undulation abgeschwächt und teils sogar in den positiven Bereich umgekehrt (wofür Island ein Beispiel zu sein scheint). Des Weiteren hängt der Effekt der dynamischen Topografie auch von der Viskosität des Erdmantels ab und ist schwierig zu quantifizieren.
Es wird auf Erkenntnisse insbesondere aus der Seismologie zurückgegriffen, um Dichten im Mantel abzuschätzen und das Geoid sowie die dynamische Topographie zu berechnen. Aus dem Vergleich mit dem beobachteten Geoid lassen sich so Rückschlüsse auf die Mantelviskosität ziehen.
Moderne Geoidlösungen
Bis etwa 1970 konnten genaue Geoidbestimmungen fast ausschließlich auf dem Festland durchgeführt werden, weshalb sie bisweilen Regionales Geoid genannt werden:
- als Astrogeoid auf Basis von Lotabweichungen, gewonnen aus einer Kombination astronomischer und geodätischer Methoden,
- andererseits als gravimetrisches Geoid mittels rasterförmigen Schweremessungen, wie sie für geodätische Präzisionsnivellements und in der Geophysik erforderlich sind,
- oder (seit den 1970er Jahren) vereinzelt als kombiniert „astro-gravimetrisches Geoid“.
Bei Methode (1) betrugen die Abstände der Messpunkte je nach angestrebter Genauigkeit (5 cm bis 50 cm) zwischen etwa 10 km und 50 km, bei (2, 3) etwa 3 bis 15 km. Seit etwa 1995 strebt man das sogenannte Zentimeter-Geoid an und hat in einigen Ländern Mitteleuropas bereits 2 bis 3 cm Genauigkeit erreicht.
Mit zunehmenden Erfolgen der Satellitengeodäsie trugen Modelle des Geopotentials (Schwerefeld im Außenraum der Erde) zur Geoidbestimmung bei. Aus den von Geoid und Erdinnerem verursachten Bahnstörungen wurden hochgradige Potentialentwicklungen mit Kugelflächenfunktionen berechnet, die anfänglich etwa 20 Breiten- und Längengrad Auflösung hatten (etwa 1000 km × 1000 km), aber nun bereits bis herab zu 0,5° (rund 50 km) reichen.
Die ersten Kugelfunktionsentwicklungen hatten globale Genauigkeiten von etwa 10 m, die sich auf weit unter 1 m verbessert haben (das sind etwa 0,00001 % des Erdradius). Im Gegensatz zu obengenannten Methoden können sie zwar keine Details auflösen, wohl jedoch ein regionales Geoid nach außen hin stützen und den Zusammenschluss zu kontinentalen Lösungen ermöglichen. Als neueste Methode dient das Satellite-to-Satellite-Tracking (STS).
Literatur
- Christoph Reigber, Peter Schwintzer: Das Schwerefeld der Erde. In: Physik in unserer Zeit. 34(5), 2003, ISSN 0031-9252, S. 206–212.
- Erwin Groten: Geodesy and the Earth’s Gravity Field. Band I: Principles and Conventional methods. Bonn 1979.
- Karl Ledersteger: Astronomische und physikalische Geodäsie (= Handbuch der Vermessungskunde. Band 5). 10. Auflage, Metzler, Stuttgart 1969.
- Gottfried Gerstbach: How to get an European centimeter geoid (“astro-geological geoid”). In: Physics and Chemistry of the Earth. Volume 21/4. Elsevier, 1996, S. 343–346.
- Heiner Denker, Jürgen Müller et al.: A new Combined Height Reference Surface for Germany (GCG05). EUREF-Conference, Riga 2006, (Poster; PDF; 414 kB).
- Hans Sünkel, I. Marson (Hrsg.): Gravity and Geoid: Joint Symposium of the International Gravity Commission and the International Geoid Commission. Tagungsband September 1995 Graz (Österreich). Springer 1996.
- Intergovernmental Committee On Surveying & Mapping: Geocentric Datum of Australia. Technical Manual, Version 2.2. (PDF-Datei, Stand: 2005).
- Wolfgang Torge: Geodäsie. 2. Auflage, Walter de Gruyter, Berlin [u. a.] 2003, ISBN 3-11-017545-2.
- Lieselotte Zenner: Analyse und Vergleich verschiedener Schwerefeldlösungen. In: Zeitschrift für Geodäsie, Geoinformation und Landmanagement. 132. Jahrgang, Heft 3. Wißner, Augsburg 2007.
Weblinks
- Norbert Kühtreiber: High Precision Geoid Determination of Austria Using Heterogeneous Data (Memento vom 21. August 2010 im Internet Archive) (Theorie; PDF; 1,6 MB)
- Stefan A. Voser: Geometrische Anforderungen beim Datenaustausch
- Umrechnung zwischen WGS84 Referenz-Ellipsoid und EGM96 Geoid
Einzelnachweise
- Axel Bojanowski: Die Erde ist eine Kartoffel, Die Welt vom 1. August 2004.
- Erwin Voellmy: Mathematische Tafeln und Formeln. 17. Auflage. Orell Füssli, Zürich 1973, ISBN 3-280-00682-1, S. 159
- Die jahreszeitliche Kartoffel gfz-potsdam.de
- Jahreszeitliche Schwankungen der planetaren "Kartoffel" messbar derstandard.at
- Die Erde ist eine Kartoffel welt.de