Trapez (Geometrie)
Ein Trapez (lateinisch trapezium von altgriechisch τραπέζιον trapézion, Verkleinerungsform von τράπεζα trapeza „Tisch“, „Vierfuß“[1]) ist in der Geometrie ein ebenes Viereck mit zwei parallel zueinander liegenden Seiten.[2]
Allgemeines
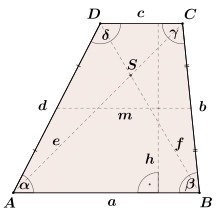
den Seiten a, b, c, d
und den Winkeln α, β, γ, δ.
Mit unterbrochenen Linien sind eingezeichnet:
die Höhe h sowie
die Diagonalen e und f des Trapezes und deren Schnittpunkt S, sowie die Mittellinie m, die die Seitenmitten von AD und BC verbindet
Die beiden parallelen Seiten werden Grundseiten des Trapezes genannt. Eine dieser Grundseiten (meistens die längere) wird oft als Basis des Trapezes bezeichnet, die beiden angrenzenden im Allgemeinen nicht parallelen Seiten oft als Schenkel. Im Trapez gibt es zwei Paare benachbarter Supplementwinkel, das heißt, die Winkel ergänzen sich zu 180 Grad.
Die Höhe des Trapezes ist der Abstand zwischen den zwei parallelen Seiten.
Jedes konvexe Trapez besitzt zwei Diagonalen, die einander im gleichen Verhältnis schneiden. Die Diagonalen teilen das Trapez in vier Dreiecke, von denen zwei zueinander ähnlich und zwei flächengleich sind. Das lässt sich so beweisen:
Sei ein konvexes Trapez und der Schnittpunkt seiner Diagonalen (siehe Abbildung), dann sind die Dreiecke und einander ähnlich, weil sie gleiche Winkel haben, denn diese Winkel sind Scheitelwinkel und Wechselwinkel bei Parallelen. Aus der Ähnlichkeit dieser beiden Dreiecke folgt direkt, dass die Diagonalen einander im gleichen Verhältnis schneiden, das heißt . Die Dreiecke und sind flächengleich, weil die Dreiecke und flächengleich sind, denn beide haben die gleiche Grundseite und die gleiche Höhe. Von beiden Dreiecken braucht nur noch das gemeinsame Dreieck abgezogen zu werden.
Ein Trapez ist entweder ein konvexes oder ein überschlagenes Viereck. Überschlagene Trapeze werden jedoch normalerweise nicht zu den Trapezen gerechnet.
Formeln
| Mathematische Formeln zum Trapez | ||
|---|---|---|
| Flächeninhalt |  | |
| Höhe | (für ),
mit | |
| Umfang | ||
| Längen der Diagonalen |
(für ) | |
| (für ) | ||
| Innenwinkel | ||
Die Formel zur Berechnung der Höhe aus den Seitenlängen lässt sich aus der heronischen Formel für die Dreiecksfläche herleiten. Die Beziehungen für die Diagonalenlängen beruhen auf dem Kosinussatz.
Spezialfälle
Gleichschenkliges und symmetrisches Trapez
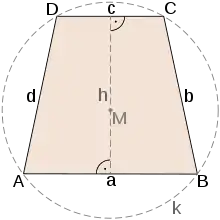
In Lehrbüchern finden sich mehrere Varianten zur Charakterisierung eines gleichschenkligen Trapezes, insbesondere:[3]
- Ein Trapez heißt gleichschenklig, wenn die beiden Seiten, die nicht Grundseiten sind, gleich lang sind.[2]
- Ein Trapez heißt gleichschenklig, wenn die beiden Innenwinkel an einer der parallelen Seiten gleich groß sind.[4][5]
- Ein Trapez heißt gleichschenklig, wenn es eine zu einer Seite senkrechte Symmetrieachse besitzt.[3]
Die erste Charakterisierung schließt formal auch Parallelogramme mit ein, die aber manchmal – wenn auch nicht ausdrücklich – ausgeschlossen werden.[6] Die letzten beiden Charakterisierungen sind gleichwertig und in diesem Fall wird das gleichschenklige Trapez wegen der Achsensymmetrie auch symmetrisches Trapez genannt. Daher sind die Innenwinkel an beiden parallelen Seiten jeweils gleich groß. Die beiden Diagonalen sind im symmetrischen Trapez gleich lang.
Die Eckpunkte eines symmetrischen Trapezes liegen auf einem Kreis , dem Umkreis des Trapezes. Das Trapez ist somit ein Sehnenviereck dieses Kreises. Der Umkreismittelpunkt ist der Schnittpunkt der Mittelsenkrechten der Seiten des Trapezes. Das Trapez wird von der Höhe , die durch den Umkreismittelpunkt geht, in zwei spiegelsymmetrische Teile zerlegt.
Ein Trapez, das zwei der Eigenschaften rechtwinklig, punktsymmetrisch (Parallelogramm) und achsensymmetrisch hat, besitzt automatisch auch die dritte und ist somit ein Rechteck.
Rechtwinkliges Trapez
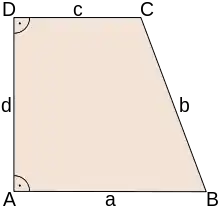
Ein Trapez heißt rechtwinklig (oder auch orthogonal), wenn es mindestens einen rechten Innenwinkel besitzt. Da in einem Trapez alle Winkel an einer der parallelen Grundseiten anliegen, muss ein rechtwinkliges Trapez immer mindestens zwei rechte Winkel besitzen, die nebeneinander liegen. Ein Rechteck ist der Spezialfall eines rechtwinkligen Trapezes. Es besitzt sogar vier rechte Innenwinkel.
Überschlagenes oder verschränktes Trapez
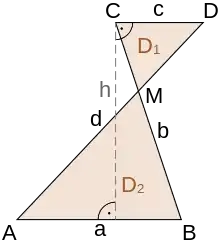
Beim überschlagenen oder verschränkten Trapez sind nicht die gleichseitigen Enden der Grundseiten durch die übrigen Seiten verbunden, sondern die gegenüber liegenden. Diese Seiten überkreuzen sich also im Mittelpunkt des Trapezes. Man kann sich ein überschlagenes Trapez vorstellen als das Viereck, das aus den Grundseiten und den Diagonalen eines konvexen Trapezes gebildet wird. Die beiden Teilflächen sind einander ähnliche Dreiecke. Überschlagene Trapeze werden jedoch normalerweise nicht zu den (normalen oder „echten“) Trapezen gezählt.
Der Flächeninhalt des überschlagenen Trapezes, das heißt die Summe der Flächeninhalte der beiden Dreiecke, berechnet sich wie folgt:
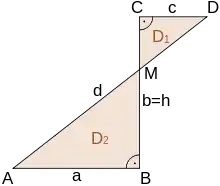
Überschlagene oder verschränkte Trapeze, die zusätzlich rechtwinklig sind, werden in der Geodäsie zur Berechnung von Flächeninhalten, beispielsweise aus Orthogonalaufnahmen, verwendet. Sie bestehen aus zwei rechtwinkligen Dreiecken, die sich an einer Ecke berühren. Die Differenz der Flächeninhalte der beiden Dreiecke ergibt sich zu
mit . Diese Fläche ist vorzeichenbehaftet. Dadurch entfallen bei Flächenberechnungen nach der Gaußschen Trapezformel Fallunterscheidungen, wenn eine Umringsseite der Fläche die Bezugslinie schneidet.
Begriffsgeschichte
Die Beschränkung des Begriffs auf Vierecke mit zwei parallelen Seiten ist relativ jung. Bis zum Beginn des 20. Jahrhunderts bezeichnete man als Trapez meist ein Viereck, in dem kein Seitenpaar parallel ist, also ein unregelmäßiges Viereck ohne besondere Eigenschaften. Für das Trapez mit zwei parallelen Seiten war die Bezeichnung Paralleltrapez üblich.[7][8] Diese Verwendung leitete sich von Euklids Klassifikation der Vierecke ab, wobei dieser ein Viereck mit einem parallelen Seitenpaar aber nicht gesondert betrachtet, sondern zu den Vierecken ohne besondere Eigenschaften gezählt hatte. Das heißt, das Trapez bei Euklid umfasste sowohl das Trapez als auch das Paralleltrapez im obigen Sinne. Euklids genaue Klassifikation lautete dabei wie folgt:
„Unter den vierseitigen Figuren heißt diejenige ein Quadrat (τετράγωνον), die gleichseitig und rechtwinklig ist; ein Rechteck (ὀρθογώνιον), die zwar rechtwinklig, aber nicht gleichseitig ist; ein Rhombus (ῥόμβος), die zwar gleichseitig, aber nicht rechtwinklig ist; und ein Rhomboid[9] (ῥομβοειδὲς σχῆμα), deren einander gegenüberliegende Seiten und Winkel gleich sind, die aber weder gleichseitig noch rechtwinklig ist. Jede andere vierseitige Figur heiße Trapez (τραπέζιον).“
Im Gegensatz dazu verwendeten Proklos, Heron und Poseidonios die Bezeichnung Trapez im modernen Sinn, also für das Paralleltrapez. Das unregelmäßige Viereck bezeichneten sie als Trapezoid (τραπεζοειδῆ).[12] Diese Unterscheidung von Trapez (engl. trapezium) und Trapezoid gibt es so im Deutschen und im britischen Englisch. Im amerikanischen Englisch werden die Begriffe trapezium und trapezoid verwirrenderweise umgekehrt verwendet.
Die meisten Mathematiker des Mittelalters ab Boethius übernahmen Euklids Verwendung des Begriffs als unregelmäßiges Viereck. Die Unterscheidung nach Poseidonios wurde nur selten wieder aufgegriffen. Erst seit dem 18. Jahrhundert findet man sie häufiger, z. B. bei Legendre und Thibaut. Jean Henri van Swinden verwendete die Bezeichnung „Trapez“ im Sinne Euklids und nannte das Viereck mit zwei parallelen Seiten Paralleltrapez.[12]
Weblinks
- Eric W. Weisstein: Trapezoid. In: MathWorld (englisch).
- Eric W. Weisstein: Trapezium. In: MathWorld (englisch).
Einzelnachweise
- Bei τράπεζα handelt es sich um eine Kurzform von τετράπεζα tetrapeza „Vierfuß“ (τέτρα tetra „vier“; πέζα peza „Fuß“). Vergleiche Karl Menninger: Zahlwort und Ziffer. Eine Kulturgeschichte der Zahl. Vandenhoeck & Ruprecht, 1979, ISBN 3-525-40725-4. S. 190 (Auszug (Google))
- Ilja N. Bronstein, Konstantin A. Semendjajew: Taschenbuch der Mathematik. 24. Auflage. Harri Deutsch, Thun und Frankfurt am Main 1989, ISBN 3-87144-492-8, S. 192.
- Bundeswettwerb Mathematik: Aufgaben und Lösungen, 1. Runde 2012. S. 8 (PDF).
- Friedrich Zech: Grundkurs Mathematikdidaktik. 10. Auflage. Beltz, Weinheim und Basel 2002, ISBN 3-407-25216-1, S. 256.
- Schülerduden: Mathematik I. Dudenverlag, 8. Auflage, Mannheim 2008, S. 457.
- In Bronstein/Semendjajew wird das gleichschenkelige Trapez zwar über die Länge der Schenkel charakterisiert, die anschließend angegebene Formel gilt jedoch nicht für Parallelogramme. In den Lösungen des Bundeswettbewerbs Mathematik 2012 werden die Charakterisierungen über Seitenlängen und Innenwinkel als Alternativen genannt. Sie sind nur gleichwertig, wenn im ersten Fall Parallelogramme ausgeschlossen werden.
- Pierer’s Universal-Lexikon. 4. Auflage 1857–1865, Artikel „Trapez“.
- Meyers Großes Konversations-Lexikon. 6. Auflage 1905–1909, Artikel „Paralleltrapēz“.
- Dabei handelte es sich also um ein „echtes“ Parallelogramm: ein Parallelogramm, das weder ein Rhombus noch ein Rechteck (und daher erst recht kein Quadrat) ist.
- Euklids Elemente. Griechischer Originaltext.
- Englische Übersetzung von Euklids Elemente (Buch I, Definition 22) mit Anmerkungen.
- Johannes Tropfke: Geschichte der Elementarmathematik. Band 4: Ebene Geometrie. de Gruyter, 1940 (f.#v=onepage eingeschränkte Vorschau in der Google-Buchsuche).