Fundamentalbereich
Ein Fundamentalbereich (auch Fundamentalregion) ist ein zusammenhängender Teilbereich eines geometrischen oder physikalischen Objekts mit Symmetrien, der so gewählt ist, dass sich keine geometrischen oder physikalischen Eigenschaften wiederholen.
Symmetrie bedeutet, dass in dem Objekt diese Eigenschaften eines Raumbereichs mehrfach vorhanden sind. In der Informationstheorie werden diejenigen Informationen, die in einer Informationsquelle mehrfach vorkommen, als redundant bezeichnet. Redundanz tritt auch bei Objekten der Geometrie und Physik auf. Ist sie auf eine Symmetrie des Objekts zurückzuführen, so ist ein Fundamentalbereich ein geeignetes Mittel zu einer Beschreibung des Objekts, die von diesen Redundanzen frei ist. In einem solchen Fall kann und sollte man sich aus pragmatischen Gründen auf einen Fundamentalbereich beschränken. Wie in der Informationstheorie auch kann Redundanz aber gewollt eingesetzt werden, etwa um Fehler in Eingabedaten und Computerprogrammen zu finden.
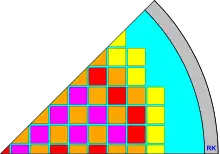
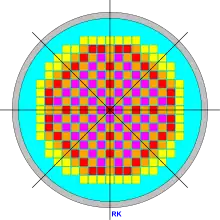
Die ersten beiden Grafiken entstammen dem Zweig der globalen Berechnungen der Reaktorphysik. Die erste zeigt einen horizontalen Querschnitt durch einen Fundamentalbereich, die zweite einen horizontalen Querschnitt durch den gesamten Reaktor (der Baureihe EPR), der durch die vier ebenfalls eingezeichneten Spiegelsymmetriegeraden in acht Fundamentalbereiche unterteilt wird.
Definition
Als Fundamentalbereich oder Fundamentalregion eines Körpers, einer ebenen geometrischen Figur oder eines eindimensionalen Objekts mit Symmetrien, die durch eine Symmetriegruppe beschrieben werden, bezeichnet man jedes zusammenhängende Gebiet, das in seinem Innern kein Paar äquivalenter Punkte enthält und sich nicht weiter vergrößern lässt, ohne diese Eigenschaft zu verlieren (David Hilbert und Stefan Cohn-Vossen, 1932).[1]
Der Mathematiker Felix Klein, dem wir bedeutende Ergebnisse in der Geometrie verdanken, definierte den Fundamentalbereich (eingeschränkt auf Punktgruppen) im Jahr 1884 so: Wir bezeichnen als Fundamentalbereich einer Gruppe von Punkttransformationen allgemein einen solchen Raumtheil, der von jeder zugehörigen Punktgruppe einen und nur einen Punkt enthält.[2]
Ein Element der Symmetriegruppe bildet einen Punkt des Fundamentalbereichs auf einen symmetrisch äquivalenten Punkt im Gesamtbereich ab. Diese beiden bilden ein Paar äquivalenter Punkte der Definition von Hilbert und Cohn-Vossen. Sie heben außerdem hervor: „Außer durch die Aufstellung der in einer Gruppe vorhandenen Drehungen und Translationen kann man jede Gruppe auch durch eine einfache geometrische Figur kennzeichnen“,[1] eben diesen Fundamentalbereich. Kennt man zum Beispiel die Positionen der Atome in einem Fundamentalbereich, so kennt man sie im ganzen Kristall.
In der Physik und Chemie, insbesondere in der Kristallographie, betrachtet man Atome, Ionen und Moleküle und abstrahiert sie gelegentlich als Punkte. Der allgemeinere Fall ist aber der, dass man Raumbereiche und nicht Punkte behandelt. Dann ist die Definition von Hilbert und Cohn-Vossen auf ein Paar äquivalenter Raumbereiche zu erweitern. Auch im Fall den abgebildeten 2D-Grafiken sind streng genommen keine flächenhaften Objekte gemeint, sondern prismatische 3D-Objekte, deren Eigenschaften nicht von der dritten Raumdimension (der „z-Achse“) des (euklidischen) Raums abhängen.
Man kann den Fundamentalbereich, den man in den Fokus stellt, aus mehreren (oder unendlich vielen) frei wählen. Anstelle des in der ersten Grafik dargestellten Fundamentalbereich hätte man auch einen der sieben anderen Symmetriesektoren der zweiten Grafik wählen können. In der numerischen Physik wird der Fundamentalbereichs oft nach praktischen und programmiertechnischen Gesichtspunkten ausgewählt, etwa: Welcher Fundamentalbereich ist anschaulich, welcher wird in einem Fachgebiet bevorzugt? Wie lassen sich Eigenschaften der Teilbereiche des Fundamentalbereichs übersichtlich in einem Feld eines Computerprogramms speichern?
Formale Definition
Ein Fundamentalbereich bezüglich einer Transformationsgruppe ist eine spezielle zusammenhängende Teilmenge eines topologischen Raumes. Seien ein topologischer Raum und eine Transformationsgruppe von . Für einen Punkt bezeichne , die Menge aller Bilder von unter den Elementen von , die Bahn (englisch Orbit) von . Dann heißt die Menge ein Fundamentalbereich von , wenn für jedes gilt, dass der Schnitt eine einelementige Menge ist.[3]
Formales Beispiel
Das Quadrat ist ein Fundamentalbereich von bezüglich der Transformationsgruppe aller Translationen um Vektoren mit ganzzahligen Komponenten. Jeder Punkt lässt sich schreiben als mit und .
Punktlagen
Punkte können nach ihrer Lage unterschieden werden. Ist der Punkt nicht Fixpunkt einer der Symmetrieoperationen, so hat er maximal viele symmetrisch äquivalente Punkte, im Fall der Diedergruppe zum Beispiel 8 (s. o.). Ist der Punkt allerdings ein Fixpunkt, liegt er zum Beispiel auf einer Spiegelsymmetriegeraden, so sind die bezüglich dieser Symmetrieoperationen symmetrisch äquivalenten Punkte mit dem Punkt selbst identisch. Im Beispiel der ersten Grafik gibt es einen Fixpunkt, den Punkt am spitzen Winkel des Kreissektors, der zum Fundamentalbereich gehört. Nicht zum Fundamentalbereich gehören alle anderen Punkte der zweiten (schrägen) Spiegelsymmetriegeraden, da sie Wiederholungen der Punkte auf der ersten Spiegelsymmetriegeraden sind.
Fundamentalbereiche in Physik und Chemie
In der Mathematik ist die Symmetrie eines Objekts und damit der Fundamentalbereich durch die Geometrie des Objekts allein festgelegt. In den Naturwissenschaften kommen, zusätzlich zu dem erwähnten Fakt, dass Raumbereiche und nicht Punkte verglichen werden, zwei weitere Aspekte hinzu:
- Die bei Anwendung einer Symmetrieoperation zu vergleichenden Raumbereiche müssen gleiche stoffliche Zusammensetzung und gleiche physikalische und chemische Eigenschaften besitzen.
- Die äußeren Randbedingungen müssen, sofern es sich um kein (zumindest im Modell) unendlich ausgedehntes Objekt handelt, die gleichen Symmetrieelemente wie die Geometrie des Objekts besitzen.
Bei der Wahl eines physikalischen Fundamentalbereichs wird man zuerst vom geometrischen ausgehen und hat dann „Füllungen“ des Raumbereichs und Randbedingungen an seiner äußeren Begrenzung einzubeziehen.
Äußere Randbedingungen
Äußere Randbedingungen sind Randbedingungen zum „Außenraum“ und sind durch die Umgebung des Objekts festgelegt. Will man zum Beispiel die Temperaturverteilung bei Abkühlung eines homogenen und homogen erwärmten Würfels (zu einem gegebenen Zeitpunkt) numerisch berechnen, ist der geometrische Fundamentalbereich des Würfels (s. u.) nur brauchbar, wenn auch die Randbedingungen passen. Wird die Temperatur des Raumbereichs um den Würfel herum konstant gehalten, ist das der Fall. Dämmt man eine Seitenfläche des Würfels, muss ein anderer, ein größerer Fundamentalbereich gewählt werden.
Nutzt man ein entsprechendes Computerprogramm, so sind die Randbedingungen meist vor Rechnungsbeginn bekannt. Sie gehören zu den Eingabedaten.
Innere Randbedingungen
Äußere Randbedingungen sind von weiteren Randbedingungen zu unterscheiden. Wird ausschließlich ein Fundamentalbereich vorgegeben, so ist allein daraus nicht immer ersichtlich, ob es sich um einen Fundamentalbereich des Symmetrietyps Punktsymmetrie, Spiegelsymmetrie, Rotationssymmetrie oder Translationssymmetrie handeln soll. Das wird durch Vorgaben an den inneren Begrenzungslinien des Fundamentalbereichs durch Randbedingungen festgelegt, die (wenn auch nicht fachübergreifend einheitlich) Symmetrierandbedingungen genannt werden.
Innere Randbedingungen werden in der Regel im Computerprogramm als Parameter festgelegt und gehören ebenfalls zu den Eingabedaten.
Beispiele aus der Kristallographie und Chemie
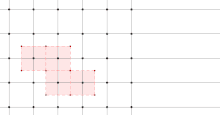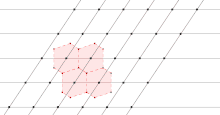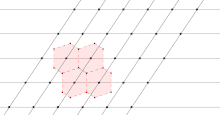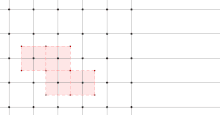
Der Fundamentalbereich wird in verschiedenen Zweigen der Physik und Chemie unterschiedlich benannt. In der Kristallographie ist eine Elementarzelle ein Fundamentalbereich in Form eines Parallelepipeds, der zu der Untergruppe der Translationssymmetrien eines Kristalls gehört. Eine Wigner-Seitz-Zelle ist in manchen Fällen ebenfalls ein Fundamentalbereich. Der Zeitschriftenartikel „On the Constitution of Metallic Sodium“[4] von Wigner und Seitz war Ausgangspunkt und Vorbild für viele nachfolgende Arbeiten, die Schrödingergleichung unter Ausnutzung von Symmetrien und Fundamentalbereichen (näherungsweise) zu lösen, um mit der daraus erhaltenen Wellenfunktion physikalische und chemische Eigenschaften von chemischen Elementen, chemischen Verbindungen und Kristallen zu berechnen. Dazu gehören Gitterkonstanten, Bindungsenergien, Verdampfungsenthalpien, Kompressibilitäten etc.
Beispiele aus der Reaktorphysik
In der Reaktorphysik werden physikalische Größen, vorrangig Neutronenflüsse und Neutronenflussspektren, für Wigner-Seitz-Zellen oder Zellen anderen Typs berechnet. Dabei werden vorhandene Symmetrien genutzt oder Symmetrien näherungsweise sogar künstlich eingeführt, etwa wird ein Quadrat durch einen flächengleichen Kreis ersetzt, um Speicherplatz und Rechenzeit zu sparen,[5] soweit das physikalisch vertretbar ist. Das ist eine Vorgehensweise, die direkt auf Wigner und Seitz zurückgeht, die ein Polyeder durch eine volumengleiche Kugel ersetzten. In den Zweigen Zellberechnungen und den eingangs erwähnten globalen Berechnungen der Reaktorphysik spielen Fundamentalbereiche eine Hauptrolle, ohne dass der von Mathematikern geprägte Name Fundamentalbereich explizit verwendet wird. Viele Kernreaktortypen werden gezielt symmetrisch konstruiert, auch deswegen, um sie überhaupt berechnen zu können, weil Symmetrien und Fundamentalbereiche den Speicherplatzbedarf und die Rechenzeiten der für Konstruktion und Betrieb notwendigen Computerprogramme (drastisch) verringern.
Beispiele für Fundamentalbereiche im dreidimensionalen euklidischen Raum
Hilbert und Cohn-Vossen hielten 1932 fest:
- „Solche Fundamentalbereiche spielen bei allen diskontinuierlichen Abbildungsgruppen eine wichtige Rolle, nicht nur bei den Bewegungsgruppen. Im allgemeinen ist es keine einfache Aufgabe, einen Fundamentalbereich für eine gegebene Gruppe zu bestimmen, oder überhaupt die Existenz eines Fundamentalbereiches für eine Gattung von Gruppen zu beweisen. Für die ebenen diskontinuierlichen Bewegungsgruppen lassen sich aber in jedem Fall leicht Fundamentalbereiche konstruieren.“[1]
In seinem achtzehnten Problem fragte Hilbert im Jahr 1900, ob es im dreidimensionalen Raum Polyeder gibt, die nicht als Fundamentalbereich einer Bewegungsgruppe auftreten, mit denen aber trotzdem der gesamte Raum lückenlos gekachelt werden kann. Dass dies der Fall ist, konnte erstmals Karl Reinhardt 1928 durch Angabe eines Falles zeigen.[6] 1932 fand dann Heinrich Heesch eine solche Lösung auch für die Ebene. Das Gebiet ist ein aktives Forschungsgebiet, zum Beispiel bei Quasikristallen nach Roger Penrose und selbstähnlichen fraktalen Parkettierungen nach William Thurston.
Fälle leicht zu konstruierender Fundamentalbereiche im dreidimensionalen euklidischen Raum sind die folgenden:
- Drehung um 180° um eine Achse: Die Bahn ist entweder eine Menge von zwei Punkten, die sich in Bezug auf die Achse gegenüberliegen, oder ein einzelner Punkt auf der Achse. Der Fundamentalbereich ist ein Halbraum, der von einer beliebigen Ebene begrenzt wird. Von dieser Ebene selbst gehört nur eine von der Achse begrenzte Halbebene zum Fundamentalbereich.
- n-fache Drehung um eine Achse: Die Bahn ist entweder eine Menge von Punkten um die Achse oder ein einzelner Punkt auf der Achse. Der Fundamentalbereich ist ein Sektor.
- Spiegelung an einer Ebene: Die Bahn ist entweder eine Menge von zwei Punkten, einer auf jeder Seite der Ebene, oder ein einzelner Punkt in der Ebene. Der Fundamentalbereich ist ein Halbraum, der von dieser Ebene begrenzt wird.
- Punktsymmetrie: Die Bahn ist eine Menge von zwei Punkten, einer auf jeder Seite des Zentrums, mit Ausnahme einer Bahn, die nur aus dem Zentrum besteht. Der Fundamentalbereich ist ein Halbraum, der von einer beliebigen Ebene durch das Zentrum begrenzt wird. Wieder gehört nur eine Halbebene zum Fundamentalbereich.
- Diskrete Translationssymmetrie in einer Richtung: Die Bahnen sind Translationen eines 1D-Gitters in Richtung des Translationsvektors. Der Fundamentalbereich ist eine unendliche Platte.
- Diskrete Translationssymmetrie in zwei Richtungen: Die Bahnen sind Verschiebungen eines 2D-Gitters in der durch die Translationsvektoren aufgespannten Ebene. Der Fundamentalbereich ist ein unendlicher Balken mit dem Querschnitt eines Parallelogramms.
- Diskrete Translationssymmetrie in drei Richtungen: Die Bahnen sind Translationen des Gitters. Der Fundamentalbereich ist eine Elementarzelle.

Bei Translationssymmetrie in Kombination mit anderen Symmetrien ist der Fundamentalbereich ein Teil der Elementarzelle. Beispielsweise ist für Wandmustergruppen der Fundamentalbereich um einen Faktor 2, 3, 4, 6, 8 oder 12 kleiner als die Elementarzelle.
Fundamentalbereiche Platonischer Körper

Etwas komplizierter ist es, die geometrische Gestalt des Fundamentalbereichs eines homogenen Würfels zu finden. Ein homogener Würfel besitzt 48 Symmetrieelemente, das neutrale Element, 23 Rotationssymmetrieelemente und Spiegelungen an 24 Symmetrieebenen. Der Würfel kann in seine 48 (äquivalenten) Fundamentalbereiche zerlegt werden, wenn man Schnitte längs der 24 Spiegelsymmetrieebenen ausführt. Das Ergebnis zeigt die Abbildung Fundamentalbereiche eines homogenen Würfels. Es gibt zwei Typen von Fundamentalbereichen, die spiegelsymmetrisch sind. Obwohl unterschiedlich eingefärbt, sind die (physikalischen) Eigenschaften der beiden Typen gleich. Ein Fundamentalbereich hat die Gestalt eines (nicht regelmäßigen) Tetraeders. Seine in der Grafik nicht sichtbaren Kanten verlaufen von den Eckpunkten des sichtbaren rechtwinkligen Dreiecks zum Fixpunkt der Symmetrieoperationen, dem Mittelpunkt des Würfels.
Die Platonischen Körper Würfel und reguläres Oktaeder sind duale Körper. Deshalb sind die Würfelgruppe und die Oktaedergruppe isomorph, da duale Körper den gleichen Symmetrietyp besitzen. Folglich besitzt auch das Oktaeder 48 Fundamentalbereiche. Gemeinsam lassen sich die Fundamentalbereiche von Würfel oder Oktaeder durch Zentralprojektion vom Fixpunkt aus auf eine umhüllende Kugel veranschaulichen, wie in der Abbildung dargestellt. Die Spiegelsymmetrieebenen schneiden die Kugel in Großkreisen. Diese Projektion der regulären Körper auf eine Kugel geht auf Felix Klein zurück, der sie bereits im ersten Abschnitt seiner berühmten Monographie eingeführt hat.[2]
Das regelmäßige homogene Tetraeder besitzt 24 Symmetrieelemente, die die Tetraedergruppe bilden. Sie ist Untergruppe der Würfelgruppe (Oktaedergruppe). Das Tetraeder hat folglich 24 Fundamentalbereiche. Der duale Körper des Tetraeders ist wieder ein Tetraeder.
Die Platonischen Körper regelmäßiges Pentagondodekaeder und regelmäßiges Ikosaeder sind dual und besitzen 120 Symmetrieelemente (Ikosaedergruppe) und 120 Fundamentalbereiche. Analog zur Abbildung Fundamentalbereiche von Würfel oder Oktaeder ist die Projektion der Fundamentalbereiche von Dodekaeder oder Ikosaeder auf eine Kugel im Artikel Ikosaedergruppe abgebildet.
Eine interessante und gut illustrierte Einführung zum Thema Fundamentalbereiche der Polyeder hat Spektrum ins Web gestellt.[7]
Siehe auch
Einzelnachweise
- David Hilbert, Stefan Cohn-Vossen: Anschauliche Geometrie. Springer, Berlin 1932, S. 56–61 (VIII, 310, eingeschränkte Vorschau in der Google-Buchsuche).
- Felix Klein: Vorlesungen über das Ikosaeder und die Auflösung der Gleichungen vom fünften Grade. Teubner, Leipzig 1884, S. 22 und 3 (VIII, 260, online).
- Fundamentalbereich. In: Guido Walz (Hrsg.): Lexikon der Mathematik. 1. Auflage. Spektrum Akademischer Verlag, Mannheim/Heidelberg 2000, ISBN 3-8274-0439-8.
- Eugene Wigner, Frederick Seitz: On the constitution of metallic sodium. In: Physical Review. Band 43, Nr. 10, 1933, S. 804 (online [PDF]).
- Samuel Glasstone, Milton C. Edlund: The elements of nuclear reactor theory. MacMillan, London 1952, S. 265 f. (VII, 416, online).
- Karl Reinhardt: Zur Zerlegung der euklidischen Räume in kongruente Polytope, Sitzungsberichte der Preussischen Akademie der Wissenschaften, 1928, S. 150–155
- Christoph Pöppe: Fundamentalbereiche auf der Kugel und das Familienregister der Polyeder. Spektrum, 28. März 2004, abgerufen am 24. August 2019.