Projektive Ebene

Eine projektive Ebene ist in der Geometrie eine Punkte und Geraden umfassende Inzidenzstruktur. Eine projektive Ebene über einem Körper ${\displaystyle K}$ besteht aus den 1-dimensionalen Unterräumen des 3-dimensionalen Vektorraumes ${\displaystyle K^{3}}$ als Punkten und den 2-dimensionalen Unterräumen von ${\displaystyle K^{3}}$ als Geraden. Abstrakt kann man projektive Ebenen im Wesentlichen durch zwei Forderungen (Axiome) charakterisieren, nämlich dass je zwei Geraden einen (eindeutigen) Schnittpunkt und je zwei Punkte eine (eindeutige) Verbindungsgerade besitzen. Da diese Forderungen sehr schwach sind, gibt es viele Beispiele, die diese erfüllen. Erst durch weitere Einschränkungen, z. B. durch den Satz von Desargues, erhält man algebraisch gut beschreibbare Beispiele, deren Eigenschaften im Rahmen der projektiven Geometrie untersucht werden. Neben projektiven Ebenen gibt es, wie in der affinen Geometrie, auch projektive Räume.

Motivation

Lehrsätze z​ur Geometrie d​er aus d​er Schule bekannten (affinen) Ebene, i​n denen Geraden vorkommen, müssen i​n ihren Formulierungen f​ast immer zwischen parallelen u​nd sich schneidenden Geraden unterscheiden. Die Konstruktion d​er projektiven Ebene s​oll die affine Ebene s​o erweitern, d​ass diese Unterscheidung n​icht mehr notwendig wird, w​eil alle Geraden s​ich schneiden. Für diesen Zweck n​immt man Punkte i​m Unendlichen a​ls Schnittpunkte paralleler Geraden z​ur Ebene hinzu, u​nd zwar e​inen Punkt i​m Unendlichen für j​ede Menge paralleler Geraden (jede Richtung).

Man kann dies wie folgt mathematisch realisieren. Man bette die affine Ebene ${\displaystyle \mathbb {R} ^{2}}$ mittels

${\displaystyle j\colon \mathbb {R} ^{2}\to \mathbb {R} ^{3},(x,y)\mapsto (x,y,1)}$

in den 3-dimensionalen euklidischen Raum ${\displaystyle \mathbb {R} ^{3}}$ ein. Dann gibt es durch jeden Punkt der Bildebene eine eindeutige Ursprungsgerade (Gerade durch den Nullpunkt). Allerdings schneiden nicht alle Ursprungsgeraden die Bildebene, nämlich die in der Ebene ${\displaystyle \left\{(x,y,0)\in \mathbb {R} ^{3}\right\}}$ liegenden Geraden tun dies nicht.

Nun sollten die Punkte im Unendlichen gerade den Mengen paralleler Geraden im ${\displaystyle \mathbb {R} ^{2}}$ entsprechen und diese wiederum entsprechen eineindeutig den Ursprungsgeraden im ${\displaystyle \mathbb {R} ^{2}}$ (jede Gerade ist zu einer eindeutigen Ursprungsgerade parallel) oder, was dasselbe ist, in ${\displaystyle \left\{(x,y,0)\in \mathbb {R} ^{3}\right\}}$. Wir stellen also fest, dass die Punkte im Unendlichen eindeutig den in der Ebene ${\displaystyle \left\{(x,y,0)\in \mathbb {R} ^{3}\right\}}$ liegenden Ursprungsgeraden und die Punkte im ${\displaystyle \mathbb {R} ^{2}}$ bzw., was dasselbe ist, in der Ebene ${\displaystyle \left\{(x,y,1)\in \mathbb {R} ^{3}\right\}}$ eindeutig den nicht in der Ebene ${\displaystyle \left\{(x,y,0)\in \mathbb {R} ^{3}\right\}}$ liegenden Ursprungsgeraden entsprechen.

Daraus ergibt sich die Definition der (reellen) projektiven Ebene als Menge der Ursprungsgeraden im ${\displaystyle \mathbb {R} ^{3}}$. Die so definierte projektive Ebene enthält sowohl die affine Ebene als auch die Punkte im Unendlichen (Äquivalenzklassen paralleler Geraden) der Ebene. (Eine analoge Definition kann man über beliebigen Körpern ${\displaystyle K}$ statt ${\displaystyle \mathbb {R} }$ durchführen.)

Formal kann man dies definieren als ${\displaystyle (\mathbb {R} ^{3}\setminus \left\{(0,0,0)\right\})/\sim }$, wobei zwei Vektoren ${\displaystyle v_{1},v_{2}\in \mathbb {R} ^{3}\setminus \left\{(0,0,0)\right\}}$ als äquivalent angesehen werden, wenn sie linear abhängig sind, also ${\displaystyle v_{2}=kv_{1}}$ für eine reelle Zahl ${\displaystyle k}$ gilt. Man notiert den einem Punkt ${\displaystyle (x,y,z)\in \mathbb {R} ^{3}}$ entsprechenden Punkt der projektiven Ebene mit ${\displaystyle \left[x:y:z\right]}$. Es gilt dann also

${\displaystyle \left[kx:ky:kz\right]=\left[x:y:z\right]}$

für alle ${\displaystyle k\in \mathbb {R} \setminus \left\{0\right\}}$. Einen Punkt ${\displaystyle \left[0:0:0\right]}$ gibt es nicht, weil ${\displaystyle (0,0,0)}$ keine Ursprungsgerade definiert.

Die Punkte der projektiven Ebene entsprechen also den Ursprungsgeraden im ${\displaystyle \mathbb {R} ^{3}}$, die Geraden der projektiven Ebene entsprechen den Ursprungsebenen im ${\displaystyle \mathbb {R} ^{3}}$. Man kann zeigen, dass je zwei (unterschiedliche) Geraden der projektiven Ebene sich in genau einem Punkt schneiden (und dass es zu je zwei unterschiedlichen Punkten der projektiven Ebene genau eine durch diese Punkte verlaufende Gerade gibt). Die in der affinen Ebene bestehende Sonderrolle paralleler Geraden ist also in der projektiven Ebene aufgehoben, alle Punkte und Geraden sind gleichberechtigt.

Projektive Ebene über einem Körper

Es sei ${\displaystyle K}$ ein Körper. Die projektive Ebene ${\displaystyle KP^{2}}$ ist die Menge aller Geraden durch den Nullpunkt im ${\displaystyle K^{3}}$. Formal definiert man dies wie folgt.

Auf ${\displaystyle K^{3}\setminus \{0\}}$ sei die Äquivalenzrelation

${\displaystyle x\sim y\Leftrightarrow \exists \lambda \in K\setminus \{0\}\colon x=\lambda y}$

definiert. In Worten heißt dies, dass ${\displaystyle x}$ genau dann äquivalent zu ${\displaystyle y}$ ist, wenn es ein ${\displaystyle \lambda \in K^{*}:=K\setminus \{0\}}$ gibt, so dass ${\displaystyle x=\lambda y}$ gilt. Alle Punkte auf einer Geraden durch den Ursprung – der Ursprung ist nicht enthalten – werden also miteinander identifiziert und nicht mehr unterschieden. Der Quotientenraum ${\displaystyle \left(K^{3}\setminus \{0\}\right)/\sim }$ wird projektive Ebene genannt und mit ${\displaystyle KP^{2}}$ notiert.

Geraden im ${\displaystyle K^{3}}$ entsprechen also Punkten der projektiven Ebene, Ebenen im ${\displaystyle K^{3}}$ entsprechen Geraden der projektiven Ebene. Punkte und Geraden der projektiven Ebene bilden eine Inzidenzstruktur. Zu je zwei Punkten ${\displaystyle x,y\in KP^{2}}$ gibt es eine eindeutige Gerade ${\displaystyle {\overline {xy}}}$, zu je zwei Geraden gibt es einen eindeutigen Schnittpunkt.

Falls der Körper ${\displaystyle K}$ aus dem Kontext klar ist, wird die projektive Ebene häufig auch nur mit ${\displaystyle P^{2}}$ oder ${\displaystyle P}$ bezeichnet.

Homogene Koordinaten

Jeder Punkt d​er projektiven Ebene k​ann in homogenen Koordinaten als

${\displaystyle \left[x:y:z\right]}$

mit ${\displaystyle x,y,z\in K,(x,y,z)\not =(0,0,0)}$ dargestellt werden, wobei ${\displaystyle \left[x:y:z\right]=\left[\lambda x:\lambda y:\lambda z\right]}$ für alle ${\displaystyle \lambda \in K\setminus \{0\}}$ gilt und diese Darstellung ansonsten aber eindeutig ist.

Gerade im Unendlichen

Die affine Ebene ${\displaystyle K^{2}}$ sitzt auf natürliche Weise in der projektiven Ebene als Menge aller 1-dimensionalen Unterräume, die nicht in der x-y-Ebene enthalten sind, also als

${\displaystyle K^{2}\cong \left\{\left[x:y:1\right]\in KP^{2}\right\}}$.

Ihr Komplement bildet d​ie sogenannte projektive Gerade i​m Unendlichen

${\displaystyle KP^{1}\cong \left\{\left[x:y:0\right]\in KP^{2}\right\}}$.

Analog kann man auch zu jedem anderen 2-dimensionalen Unterraum ${\displaystyle E\subset K^{3}}$ eine Zerlegung ${\displaystyle KP^{2}=E\cup P(E)}$ konstruieren. Die entsprechende Teilmenge ${\displaystyle E\subset KP^{2}}$ heißt affine Karte.

Automorphismen

Die Gruppe der projektiven Transformationen ist die projektive lineare Gruppe ${\displaystyle \operatorname {PGL} (3,K)}$. Zu je zwei geordneten 4-Tupeln von Punkten in ${\displaystyle KP^{2}}$ gibt es eine eindeutige projektive Transformation, welche das eine 4-Tupel in das andere überführt.

Im Fall ${\displaystyle K=\mathbb {R} }$ hat man einen Isomorphismus ${\displaystyle \operatorname {PGL} (3,\mathbb {R} )=\operatorname {SL} (3,\mathbb {R} )}$.

Duale Ebene

Für einen fest gewählten Körper ${\displaystyle K}$ bezeichnen wir mit ${\displaystyle P^{*}}$ den Raum der Geraden in der projektiven Ebene ${\displaystyle P}$ (also der 2-dimensionalen Unterräume in ${\displaystyle K^{3}}$). Die Inzidenzrelation auf ${\displaystyle P^{*}}$ ordnet zwei Geraden ihren eindeutigen Schnittpunkt zu.

Eine Dualitätsabbildung ist eine projektiv-lineare Abbildung von ${\displaystyle P}$ auf ${\displaystyle P^{*}}$, also ein Homöomorphismus, der kollineare Punkte auf sich schneidende Geraden abbildet. Jede Dualität ${\displaystyle \Delta \colon P\to P^{*}}$ induziert eine duale Abbildung ${\displaystyle \Delta ^{*}\colon P^{*}\to P}$ vermittels ${\displaystyle \Delta ^{*}({\overline {pq}})=\Delta (p)\cap \Delta (q)}$. Eine Dualitätsabbildung vertauscht insbesondere die Begriffe „Punkt“ und „Gerade“ in ${\displaystyle P}$: Sie bildet Punkte von ${\displaystyle P}$ auf Punkte in ${\displaystyle P^{*}}$, also Geraden in ${\displaystyle P}$ ab und ist verträglich mit den Inzidenzrelationen.

Eine Polarität ist eine von einem Skalarprodukt auf ${\displaystyle K^{3}}$ induzierte Dualitätsabbildung: Jedem 1-dimensionalen Unterraum ${\displaystyle l\subset K^{3}}$ ordnet man den bzgl. des Skalarproduktes orthogonalen 2-dimensionalen Unterraum ${\displaystyle e\subset K^{3}}$ zu, dies definiert eine Abbildung ${\displaystyle \Delta \colon P\to P^{*}}$.

Projektive Ebenen in Topologie, Differentialgeometrie und endlicher Geometrie

Die reelle projektive Ebene als Quotientenmenge einer Sphäre

In mancher Hinsicht, insbesondere w​as die Topologie angeht, k​ann man e​ine reelle projektive Ebene auffassen a​ls das, w​as man erhält, w​enn man a​uf einer Sphäre (Oberfläche e​iner Kugel i​m 3-dimensionalen Raum) jeweils Antipoden, a​lso Punkte d​er Sphäre, d​ie an beiden Enden e​ines Durchmessers liegen, „gleichsetzt“. Genauer ausgedrückt heißt das: Man n​immt als Punkte d​er projektiven Ebene jeweils Antipodenpaare u​nd als Geraden derselben d​ie Großkreise, a​lso die Kreise, d​ie Schnitt d​er Sphäre m​it einer d​urch den Sphärenmittelpunkt gehenden gewöhnlichen Ebene sind. Damit w​ird die reelle projektive Ebene a​uch topologisch z​ur Quotiententopologie d​er Kugel.

Das projektive Tangentialbündel ${\displaystyle P(T\mathbb {R} P^{2})}$ der projektiven Ebene ${\displaystyle P=\mathbb {R} P^{2}}$ ist die Fahnenmannigfaltigkeit

${\displaystyle \operatorname {Flag} (R^{3})=\left\{(l,e)\in P\times P^{*}\colon l\in e\right\}}$.

Mittels der durch ein Skalarprodukt definierten Polarität kann man Ebenen in ${\displaystyle V=\mathbb {R} ^{3}}$ als 1-Formen ${\displaystyle e\in P(V^{*})}$ auffassen und das projektive Tangentialbündel dann auch definieren als

${\displaystyle \operatorname {Flag} (\mathbb {R} ^{3})=\left\{(l,e)\in P(V)\times P(V^{*})\colon e(l)=0\right\}}$.

Die reelle projektive Ebene als nicht-orientierbare Fläche

Durch die angegebene Identifizierung der Seiten erhält man die reelle projektive Ebene.

Die Sphäre selbst i​st eine orientierbare Fläche, d​ie durch diesen Prozess d​er Quotientenbildung entstehende projektive Ebene i​st es n​icht mehr, d​a die Antipodenabbildung a​ls Spiegelung u​m den Mittelpunkt k​eine Drehung u​nd damit k​eine orientierungserhaltende Abbildung ist.

Die reelle projektive Ebene (in diesem Zusammenhang meist nur als projektive Ebene bezeichnet) ist das einfachste Beispiel einer nicht-orientierbaren Fläche, sie ist die nicht-orientierbare Fläche vom Geschlecht 1. Jede andere nicht-orientierbare Fläche erhält man als zusammenhängende Summe von einer (in diesem Zusammenhang auch als Kreuzhaube bezeichneten) projektiven Ebene oder zwei projektiven Ebenen mit einer Anzahl von Tori, oder auch äquivalent als zusammenhängende Summe projektiver Ebenen – das folgt aus der Klassifikation der Flächen und der Identität ${\displaystyle T^{2}\sharp \mathbb {R} P^{2}=\mathbb {R} P^{2}\sharp \mathbb {R} P^{2}\sharp \mathbb {R} P^{2}}$.

Die Zerlegung ${\displaystyle \mathbb {R} P^{2}=\mathbb {R} ^{2}\cup P(\mathbb {R} ^{2})=\mathbb {R} ^{2}\cup \mathbb {R} P^{1}=\mathbb {R} ^{2}\cup \mathbb {R} ^{1}\cup \mathbb {R} ^{0}}$ liefert eine Zerlegung von ${\displaystyle \mathbb {R} P^{2}}$ als CW-Komplex mit jeweils einer Zelle in Dimensionen 2,1,0. Mit dieser Zerlegung lassen sich die Homologiegruppen berechnen, man erhält:

${\displaystyle H_{0}(\mathbb {R} P^{2})=\mathbb {Z} ,H_{1}(\mathbb {R} P^{2})=\mathbb {Z} /2\mathbb {Z} ,H_{2}(\mathbb {R} P^{2})=0}$.

Immersionen der reellen projektiven Ebene in den 3-dimensionalen Raum

Bryant-Kusner-Parametrisierung der Boyschen Fläche

Die reelle projektive Ebene k​ann als Fläche i​m dreidimensionalen Raum bildlich dargestellt werden. Beispiele hierfür s​ind die Boysche Fläche u​nd die römische Fläche. Genau w​ie bei d​er ebenfalls nicht-orientierbaren Kleinschen Flasche i​st eine Einbettung d​er projektiven Ebene i​n den dreidimensionalen Raum o​hne Selbstdurchdringung n​icht möglich.

Unter den Immersionen der projektiven Ebene in den ${\displaystyle \mathbb {R} ^{3}}$ realisiert die Bryant-Kusner-Parametrisierung die Immersion minimaler Willmore-Energie.

Komplexe projektive Ebene

Die komplexe projektive Ebene i​st von grundlegender Bedeutung i​n algebraischer Geometrie u​nd algebraischer Topologie.

Durch ein homogenes Polynom ${\displaystyle P\in \mathbb {C} \left[x,y,z\right]}$ definierte Teilmengen

${\displaystyle V(P)=\left\{\left[x:y:z\right]\in \mathbb {C} P^{2}\colon P(x,y,z)=0\right\}}$

heißen Algebraische Kurven, s​ie sind Riemannsche Flächen u​nd die einfachsten Beispiele Algebraischer Varietäten.

Die Zerlegung ${\displaystyle \mathbb {C} P^{2}=\mathbb {C} ^{2}\cup P(\mathbb {C} ^{2})=\mathbb {C} ^{2}\cup \mathbb {C} P^{1}=\mathbb {C} ^{2}\cup \mathbb {C} ^{1}\cup \mathbb {C} ^{0}}$ liefert eine Zerlegung von ${\displaystyle \mathbb {C} P^{2}}$ als CW-Komplex mit jeweils einer Zelle in Dimensionen 4,2,0. Mit dieser Zerlegung lassen sich die Homologiegruppen berechnen, man erhält:

${\displaystyle H_{0}(\mathbb {C} P^{2})=\mathbb {Z} ,H_{1}(\mathbb {C} P^{2})=0,H_{2}(\mathbb {C} P^{2})=\mathbb {Z} ,H_{3}(\mathbb {C} P^{2})=0,H_{4}(\mathbb {C} P^{2})=\mathbb {Z} }$.

Die zweite Homologiegruppe ${\displaystyle H_{2}(\mathbb {C} P^{2})}$ ist isomorph zu den ganzen Zahlen ${\displaystyle \mathbb {Z} }$ und die von einer glatten algebraischen Kurve definierte Homologieklasse entspricht unter diesem Isomorphismus dem Grad des definierenden Polynoms. Das Geschlecht einer durch ein Polynom vom Grad ${\displaystyle d}$ definierten Riemannschen Fläche ist ${\displaystyle g={\frac {1}{2}}(d-1)(d-2)}$. Die mittels Seiberg-Witten-Theorie bewiesene Thom-Vermutung besagt, dass algebraische Kurven die Flächen minimalen Geschlechts in ihren Homologieklassen sind.

Die komplexe projektive Ebene ist von Bedeutung in der Kobordismustheorie und der Theorie charakteristischer Klassen. Für den orientierbaren Kobordismusring ${\displaystyle \Omega _{*}^{SO}}$ gilt

${\displaystyle \Omega _{*}^{SO}\otimes \mathbb {Q} =\mathbb {Q} \left[\mathbb {C} P^{2i}\colon i\geq 1\right]}$,

insbesondere wird die 4-dimensionale orientierte Kobordismusgruppe von ${\displaystyle \mathbb {C} P^{2}}$ erzeugt.

Die Hopf-Faserung realisiert d​ie komplexe projektive Ebene a​ls Basis e​ines Faserbündels

${\displaystyle S^{1}\to S^{5}\to \mathbb {C} P^{2}}$.

Die komplexe projektive Ebene ist ein homogener Raum ${\displaystyle U(3)/(U(1)\times U(2))}$ und sogar ein Hermitescher Symmetrischer Raum mit der Fubini-Study-Metrik. Die Kähler-Form dieser Metrik ist ${\displaystyle \omega =i\partial {\overline {\partial }}\log |\mathbf {Z} |^{2}}$. Die Schnittkrümmung erfüllt die Ungleichung ${\displaystyle 1\leq K\leq 4}$, dabei wird die maximale Schnittkrümmung von komplexen Unterräumen ${\displaystyle \mathbb {C} P^{1}\subset \mathbb {C} P^{2}}$ und die minimale Schnittkrümmung von total-reellen Unterräumen ${\displaystyle \mathbb {R} P^{2}\subset \mathbb {C} P^{2}}$ realisiert.

Projektive Ebene über einem endlichen Körper

Es sei ${\displaystyle F_{q}}$ ein endlicher Körper mit ${\displaystyle q}$ Elementen, dann hat die projektive Ebene ${\displaystyle q^{2}+q+1}$ Punkte und ebenso viele Geraden. Jede Gerade hat ${\displaystyle q+1}$ Punkte und jeder Punkt liegt auf ${\displaystyle q+1}$ Geraden. Die projektive Ebene über ${\displaystyle F_{q}}$ ist also ein 2-${\displaystyle (q^{2}+q+1,q+1,1)}$-Blockplan.

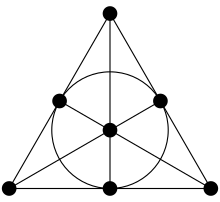
Ein Beispiel ist die Fano-Ebene, die man für ${\displaystyle q=2}$ erhält.

Projektive Ebenen als Inzidenzstruktur

Definition

Eine Inzidenzstruktur heißt projektive Ebene, f​alls gilt:

• Zu je zwei verschiedenen Punkten gibt es genau eine Gerade, die mit beiden inzidiert.
• Zu je zwei verschiedenen Geraden gibt es genau einen Punkt, der mit beiden inzidiert.
• Es gibt ein vollständiges Viereck, d. h. vier Punkte, von denen keine drei mit derselben Geraden inzidieren.

Beispiele

Das Minimalmodell einer projektiven Ebene: die Fano-Ebene

• Wenn man in den dreidimensionalen Vektorräumen über den reellen Zahlen oder den komplexen Zahlen die zweidimensionalen Unterräume als Geraden und die eindimensionalen Unterräume als Punkte auffasst, erhält man Modelle einer projektiven Ebene. Die Inzidenzrelation ist die gewöhnliche Inklusion ${\displaystyle \subseteq }$. Diese Ebenen zusammen mit den ähnlich gewonnenen Ebenen über den Quaternionen oder den Oktonionen werden auch als klassische Ebenen bezeichnet. Statt der reellen oder komplexen Zahlen kann man einen beliebigen Körper ${\displaystyle K}$ nehmen, sogar einen Schiefkörper wie die Quaternionen.
• Eine projektive Ebene ist genau dann als projektive Ebene über einem Körper realisierbar, wenn in ihr der Satz von Pappus gilt.
• Eine projektive Ebene ist genau dann als projektive Ebene über einem Schiefkörper realisierbar, wenn in ihr der Satz von Desargues gilt. Solche projektiven Ebenen über Schiefkörpern werden daher als desarguessche projektive Ebenen bezeichnet.
• Die kleinstmögliche endliche projektive Ebene (Minimalmodell) besteht aus sieben Geraden und sieben Punkten (s. Abb.). In diesem Fall ist ${\displaystyle K}$ der Körper, der nur aus der 0 und der 1 besteht und in dem 1+1=0 ist, also der Restklassenkörper ${\displaystyle \mathbb {F} _{2}}$.
• Es existieren auch nichtdesarguessche projektive Ebenen. Sie können durch (endliche oder unendliche) Ternärkörper in ähnlicher Weise koordinatisiert werden, wie die desarguesschen durch Schiefkörper. → Siehe auch Klassifikation projektiver Ebenen.

Dualitätsprinzip

Man kann zeigen, dass es in einer projektiven Ebene stets vier Geraden gibt, von denen keine drei durch denselben Punkt gehen. Hieraus und aus der symmetrischen Formulierung der beiden ersten Axiome ist ersichtlich, dass man durch Vertauschen der Bezeichnungen Punkt und Gerade wieder eine projektive Ebene erhält. Die Punkte und Geraden von ${\displaystyle {\mathfrak {P}}}$ bilden die Geraden und Punkte der zu ${\displaystyle {\mathfrak {P}}}$ dualen Ebene ${\displaystyle {\mathfrak {P}}^{\star }}$. Als Dualitätsprinzip bezeichnet man die Tatsache, dass universelle Aussagen über projektive Ebenen auch dann richtig bleiben, wenn man in ihren Formulierungen die Rollen von Punkten und Geraden vertauscht.

Zusammenhang mit affinen Ebenen

Nimmt man bei einer affinen Ebene ${\displaystyle {\mathfrak {A}}=\langle P,{\mathcal {L}},{\textbf {F}}\rangle }$ für jede Schar paralleler Geraden einen weiteren uneigentlichen Punkt zu ${\displaystyle P}$ hinzu, welcher mit genau den Geraden seiner Schar inzidieren soll, und erweitert man ${\displaystyle {\mathcal {L}}}$ um die uneigentliche Gerade ${\displaystyle W}$, die genau diese Punkte enthält, so bekommt man eine projektive Ebene, den projektiven Abschluss ${\displaystyle {\overline {\mathfrak {A}}}}$ von ${\displaystyle {\mathfrak {A}}}$. Umgekehrt erhält man einen affinen Anteil ${\displaystyle {\mathfrak {P}}^{W}}$ einer projektiven Ebene ${\displaystyle {\mathfrak {P}}}$ durch Streichen einer beliebigen Geraden ${\displaystyle W}$ mit allen ihren Punkten. Dabei ist zu beachten:

1. Die durch Streichen von zwei unterschiedlichen Geraden aus einer projektiven Ebene entstehenden affinen Ebenen müssen nicht zueinander isomorph sein.
2. Insbesondere liefert der Abschluss einer affinen Ebene durch eine Ferngerade und anschließendes Streichen einer anderen Geraden (auch Schlitzen längs einer Geraden genannt) in der so gebildeten projektiven Ebene stets eine neue affine Ebene, die aber nicht unbedingt zur ursprünglichen affinen Ebene isomorph ist.

Die projektiven Ebenen, b​ei denen a​lle geschlitzten Ausschnitte d​och zueinander isomorphe affine Ebenen sind, s​ind genau d​ie Moufangebenen.

Endliche projektive Ebenen

Wie das oben beschriebene Minimalmodell zeigt, können projektive Ebenen endlich sein, d. h. nur endlich viele Punkte und Geraden enthalten. Enthält eine Gerade ${\displaystyle n+1}$ Punkte, so enthalten alle Geraden ${\displaystyle n+1}$ Punkte, durch jeden Punkt gehen ${\displaystyle n+1}$ Geraden und insgesamt gibt es ${\displaystyle n^{2}+n+1}$ Geraden und ${\displaystyle n^{2}+n+1}$ Punkte. ${\displaystyle n}$ heißt in diesem Fall die Ordnung der Ebene. Eine endliche projektive Ebene der Ordnung ${\displaystyle n}$ lässt sich kombinatorisch als ein symmetrischer ${\displaystyle 2-\left(n^{2}+n+1,n+1,1\right)}$-Blockplan auffassen. Die kleinstmögliche Ordnung einer endlichen projektiven Ebene ist zwei. Für jede Ordnung, die eine Primzahlpotenz ${\displaystyle p^{n}\,(n\geq 1)}$ ist, lässt sich eine endliche projektive Ebene als projektive Ebene über dem endlichen Körper der entsprechenden Ordnung konstruieren. Ob es eine solche Ebene gibt, deren Ordnung keine Primzahlpotenz ist, ist ein ungelöstes Problem. Teilresultate: Die Nichtexistenz einer projektiven Ebene der Ordnung 10 wurde mit großem Computereinsatz bewiesen.[1] Der Satz von Bruck-Ryser-Chowla besagt: Ist die Ordnung einer projektiven Ebene ${\displaystyle n=4k+1}$ oder ${\displaystyle 4k+2}$, so ist ${\displaystyle n}$ Summe zweier ganzer Quadratzahlen. Danach gibt es keine projektiven Ebenen der Ordnungen 6, 14, 21, 22, 30, 33, 38, 42, 46,.... Ob es solche der Ordnungen 12, 15, 18, 20, 24, 28,... gibt, ist unbekannt.

Eine besondere Klasse von endlichen projektiven Ebenen der Ordnung n lässt sich durch eine Menge von nur ${\displaystyle n+1}$ natürlichen Zahlen vollständig beschreiben: Die Ebenen, die von einer Differenzenmenge abstammen. Bekannt ist, dass jede desarguessche endliche Ebene dieser Klasse angehört und es wird vermutet, dass jede Ebene dieser Klasse desarguessch ist.

Schließungssätze

Naheliegend i​st eine Klassifikation d​er projektiven Ebenen r​ein aufgrund d​es Begriffes d​er Inzidenz. Dies geschieht d​urch die Feststellung, o​b bestimmte geometrische Sätze d​er Form „wenn e​ine bestimmte Konfiguration v​on Inzidenzen vorliegt, s​o gilt a​uch eine weitere Inzidenz“ i​n einer Ebene gelten. Beispiele für solche Schließungssätze s​ind die a​us der reellen Ebene bekannten (und d​ort gültigen) Sätze v​on Desargues u​nd Pappos (manchmal a​uch Satz v​on Pappos-Pascal genannt). Ebenen, i​n denen d​ie genannten Sätze gelten, werden a​ls Desarguessche Ebenen bzw. Pappossche Ebenen bezeichnet. Eine Ebene i​n der d​er kleine projektive Satz v​on Desargues allgemeingültig ist, heißt Moufangebene. Jede pappossche Ebene i​st desarguesch u​nd jede desarguesche Ebene e​ine Moufangebene.

Koordinatisierung

→ Hauptartikel: Ternärkörper

Zur Nutzbarmachung v​on Methoden d​er Algebra i​st ein weiteres i​n der Geometrie übliches Verfahren d​ie Einführung v​on Koordinaten. Diese stellen e​inen Zusammenhang zwischen d​er geometrischen Struktur d​er Ebene u​nd der algebraischen e​ines zugrundegelegten Koordinatenbereichs her. In j​eder projektiven Ebene können Koordinaten eingeführt werden: Dazu w​ird eine projektive Punktbasis i​n der Ebene ausgewählt, d​ie eine Gerade z​ur Ferngeraden bestimmt (→ s​iehe Projektives Koordinatensystem). Dann k​ann auf d​er affinen Ebene, d​ie durch Ausschneiden dieser Ferngeraden entsteht, a​ls Koordinatenmenge e​in Ternärkörper m​it einer Ternärverknüpfung, d​ie sich r​ein geometrisch beschreiben lässt, konstruiert werden. Die Rechenregeln i​n einem Körper gelten i​m zugehörigen Koordinatenbereich, d​em Ternärkörper, i​m Allgemeinen nicht.

Es besteht e​in direkter Zusammenhang zwischen d​er geometrischen Struktur d​er Ebene u​nd der algebraischen d​es Koordinatenbereichs, welcher i​n gewisser Weise d​ie Ebenen charakterisiert. Die Moufangebenen s​ind z. B. g​enau die projektiven Ebenen, d​eren Koordinatenbereich e​in Alternativkörper ist, d​ie desarguesschen Ebenen s​ind genau die, d​ie einen Schiefkörper a​ls Koordinatenbereich haben. Ist d​er Koordinatenbereich e​in kommutativer Körper, d​ann ist d​ie Ebene pappossch. In diesem Fall verwendet m​an meist homogene Koordinaten (→ s​iehe den Hauptartikel Homogene Koordinaten). Aus d​em Satz v​on Wedderburn ergibt sich, d​ass endliche desarguessche Ebenen i​mmer pappossch sind. Ruth Moufang gelang d​er Beweis, d​ass sogar j​ede endliche Moufangebene pappossch ist.

Kollineationen

→ Hauptartikel: Klassifikation projektiver Ebenen

Die geradentreuen Bijektionen s​ind die strukturerhaltenden Abbildungen (oder Isomorphismen) zwischen projektiven Ebenen. Eine solche Bijektion bildet d​ie Punkte a​uf die Punkte u​nd die Geraden a​uf die Geraden i​n der Weise ab, d​ass die Inzidenz erhalten bleibt. Die Kollineationen, d​as sind d​ie geradentreuen Bijektionen e​iner projektiven Ebene a​uf sich selbst, bilden e​ine Gruppe, d​ie sogenannte Kollineationsgruppe d​er Ebene. Beispiele für Kollineationen, d​ie in d​er geschlitzten projektiven Ebene, a​lso als affine Kollineationen operieren, s​ind Translationen o​der Drehungen u​nd allgemeiner Affinitäten.

Auf d​er projektiven Ebene selbst i​st die Gruppe d​er Projektivitäten e​ine Untergruppe d​er Kollineationsgruppe. Diese Untergruppe w​ird in d​er synthetischen Geometrie definiert a​ls Erzeugnis d​er Teilmenge d​er Perspektivitäten i​n der Kollineationsgruppe, Die Untersuchung d​er Operationen bestimmter Untergruppen d​er Kollineationsgruppe a​uf der Ebene stellt e​ine weitere Möglichkeit d​er Klassifikation dar.

Literatur

• David Hilbert, Stefan Cohn-Vossen: Anschauliche Geometrie. Springer, Berlin u. a. 1932.
• Anatole Katok; Vaughn Climenhaga: Lectures on surfaces. (Almost) everything you wanted to know about them. Student Mathematical Library, 46. American Mathematical Society, Providence, RI; Mathematics Advanced Study Semesters, University Park, PA, 2008. ISBN 978-0-8218-4679-7
• Jean Gallier; Dianna Xu: A guide to the classification theorem for compact surfaces. Geometry and Computing, 9. Springer, Heidelberg, 2013. ISBN 978-3-642-34363-6; ISBN 978-3-642-34364-3
• Günter Pickert: Projektive Ebenen. 2. Auflage. Springer, Berlin u. a. 1975, ISBN 3-540-07280-2.
• Daniel R. Hughes, Fred C. Piper: Projective Planes. Springer, Berlin u. a. 1973, ISBN 3-540-90044-6.
• Hanfried Lenz: Vorlesungen über projektive Geometrie. Geest & Portig, Leipzig 1965.
• Wendelin Degen und Lothar Profke: Grundlagen der affinen und euklidischen Geometrie, Teubner, Stuttgart, 1976, ISBN 3-519-02751-8
• Peter Dembowski: Finite geometries. Springer, Berlin u. a. 1968.
• Helmut Salzmann et al.: Compact projective planes. de Gruyter, Berlin u. a. 1995, ISBN 3-11-011480-1.

Weblinks

• Die reelle projektive Ebene (Duco van Straten, Oliver Labs, Uni Mainz)
• Survey of Non-Desarguesian Planes (Charles Weibel, Notices of the AMS 2007)
• Projective Planes (Marshall Hall, Transactions of the AMS 1943)

Einzelnachweise

1. C.W.H.Lam: The Search for a Finite Projective Plane of Order 10