Faserbündel

Ein Faserbündel ist in der Mathematik, speziell in der Topologie, ein Raum, der lokal wie ein Produkt aussieht: Faserbündel kann man als stetige surjektive Abbildungen ${\displaystyle \pi \colon E\to B}$ mit einer lokalen Trivialitätsbedingung auffassen: Für jeden Punkt von ${\displaystyle B}$ gibt es eine Umgebung ${\displaystyle U}$, für die die Einschränkung ${\displaystyle \pi |_{\pi ^{-1}(U)}}$ Projektion eines Produkts ${\displaystyle U\times F}$ mit einer Faser ${\displaystyle F}$ ist.

${\displaystyle E,B}$ und ${\displaystyle F}$ heißen Totalraum, Basis und Faser des Bündels. Es gibt verschiedene den Begriff des Faserbündels verallgemeinernde Begriffe von Faserungen, insbesondere Serre- und Hurewicz-Faserungen.

Spezielle Faserbündel s​ind z. B. Vektorbündel, welche e​ine fundamentale Rolle b​ei der mathematischen Formulierung d​er physikalischen Eichtheorie spielen.

Definition

Ein Faserbündel wird durch die Daten ${\displaystyle (E,B,\pi ,F)}$ spezifiziert, wobei ${\displaystyle E}$, ${\displaystyle B}$ und ${\displaystyle F}$ topologische Räume sind und die Projektion ${\displaystyle \pi \colon E\to B}$ eine stetige surjektive Abbildung ist, welche lokal trivialisierbar ist, d. h. es existiert für jeden Punkt ${\displaystyle x}$ in ${\displaystyle B}$ eine offene Umgebung ${\displaystyle U}$, so dass ${\displaystyle \pi ^{-1}(U)}$ homöomorph zum Raum ${\displaystyle U\times F}$, versehen mit der Produkttopologie, ist, und das folgende Diagramm kommutiert:

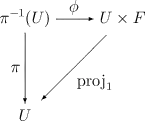
wobei ${\displaystyle \operatorname {proj} _{1}\colon U\times F\to U}$ die natürliche Projektion auf den ersten Faktor und ${\displaystyle \phi \colon \pi ^{-1}(U)\to U\times F}$ ein Homöomorphismus ist. Die Menge aller solcher ${\displaystyle \{(U_{i},\phi _{i})\}}$ nennt man lokale Trivialisierung des Bündels, die ${\displaystyle U_{i}}$ überdecken definitionsgemäß die Basis.

Für jedes ${\displaystyle x}$ aus ${\displaystyle B}$ ist das Urbild ${\displaystyle \pi ^{-1}(x)}$ homöomorph zu ${\displaystyle F}$ und heißt Faser über ${\displaystyle x}$. Ein Faserbündel ${\displaystyle (E,B,\pi ,F)}$ wird oft durch die kurze exakte Sequenz ${\displaystyle F\longrightarrow E\ {\xrightarrow {\,\ \pi \ }}\ B}$ dargestellt. Man beachte, dass jedes Faserbündel ${\displaystyle \pi \colon E\to B}$ eine offene Abbildung ist, da Projektionen von Produkten offene Abbildungen sind. Daher trägt ${\displaystyle B}$ die durch die Abbildung ${\displaystyle \pi }$ induzierte Quotiententopologie.

Ein Faserbündel i​st ein Spezialfall e​iner Serre-Faserung, d​as heißt, e​s besitzt d​ie sogenannte Homotopie-Hochhebungseigenschaft für Abbildungen v​on CW-Komplexen.

Bündelabbildungen

Eine Bündelabbildung zwischen zwei Bündeln ${\displaystyle \pi _{1}\colon E_{1}\to B_{1}}$ und ${\displaystyle \pi _{2}\colon E_{2}\to B_{2}}$ besteht aus zwei Abbildungen

${\displaystyle \phi \colon E_{1}\to E_{2}}$ und ${\displaystyle f\colon B_{1}\to B_{2}}$

mit

${\displaystyle f\circ \pi _{1}=\pi _{2}\circ \phi }$.

Zwei Bündel ${\displaystyle \pi _{1}\colon E_{1}\to B_{1}}$ und ${\displaystyle \pi _{2}\colon E_{2}\to B_{2}}$ heißen äquivalent, wenn es Bündelabbildungen

${\displaystyle (\phi ,f)\colon (E_{1},B_{1})\to (E_{2},B_{2})}$ und ${\displaystyle (\psi ,g)\colon (E_{2},B_{2})\to (E_{1},B_{1})}$

mit

${\displaystyle \phi \circ \psi =id_{E_{2}}}$ und ${\displaystyle \psi \circ \phi =id_{E_{1}}}$

gibt.

Beispiele

Das Möbiusband ist ein nichttriviales Bündel über S¹ mit Faser [0,1].

Die Kleinsche Flasche ist ein nichttriviales Bündel über S¹ mit Faser S¹.

Sei ${\displaystyle E=B\times F}$ und ${\displaystyle \pi \colon E\to B}$ die Projektion auf den ersten Faktor. Dann ist ${\displaystyle E}$ ein Faserbündel über ${\displaystyle B}$ mit Faser ${\displaystyle F}$. In diesem Fall ist ${\displaystyle E}$ nicht nur lokal ein Produktraum, sondern sogar global. Man bezeichnet ${\displaystyle E=B\times F}$ als triviales Bündel und ein zu diesem äquivalentes als trivialisierbares Bündel.

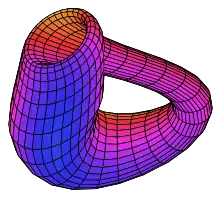
Ein einfaches Beispiel eines nichttrivialen Bündels ist das Möbiusband. Die Basis ${\displaystyle B}$ ist hier ${\displaystyle S^{1}}$ (die Kreislinie), die Faser ${\displaystyle F}$ ein abgeschlossenes Intervall. Das entsprechende triviale Bündel wäre ein Zylinder, von dem sich das Möbiusband durch ein Verdrehen der Faser unterscheidet. Diese Verdrehung ist nur global sichtbar, lokal sind Zylinder und Möbiusband identisch.

Ein ähnliches nichttriviales Bündel ist die Kleinsche Flasche, welche eine ${\displaystyle S^{1}}$-Faserung über ${\displaystyle S^{1}}$ darstellt. Das entsprechende triviale Bündel wäre ein Torus. Jedes Faserbündel über ${\displaystyle S^{1}}$ ist ein Abbildungstorus.

Jede Überlagerung e​ines zusammenhängenden Raumes i​st ein Faserbündel m​it einer diskreten Faser.

Eine spezielle Klasse v​on Faserbündeln, d​ie Vektorbündel, s​ind dadurch ausgezeichnet, d​ass ihre Fasern Vektorräume u​nd die Trivialisierungen faserweise linear sind. Wichtige Beispiele s​ind hier d​ie Tangential- u​nd Kotangentialbündel e​iner Mannigfaltigkeit.

Eine weitere spezielle Klasse v​on Faserbündeln s​ind die Prinzipalbündel o​der Hauptfaserbündel.

Schnitte

→ Hauptartikel: Schnitt (Faserbündel)

Unter einem globalen Schnitt versteht man eine stetige Abbildung ${\displaystyle f\colon B\to E}$, so dass ${\displaystyle \pi (f(x))=x}$ für alle ${\displaystyle x}$ aus ${\displaystyle B}$. Die Theorie der charakteristischen Klassen in der Algebraischen Topologie beschäftigt sich mit der Existenz von globalen Schnitten.

Oft kann man Schnitte nur lokal definieren. Ein lokaler Schnitt ist eine stetige Abbildung ${\displaystyle f\colon U\to E}$, wobei ${\displaystyle U}$ eine offene Menge in ${\displaystyle B}$ ist und ${\displaystyle \pi (f(x))=x}$ für alle ${\displaystyle x}$ aus ${\displaystyle U}$. Für eine lokale Trivialisierung ${\displaystyle (U,\phi )}$ ist dies immer möglich. Diese Schnitte sind äquivalent mit stetigen Abbildungen ${\displaystyle U\to F}$, welche eine Garbe bilden.

Strukturgruppen

Faserbündel werden bis auf topologische Äquivalenz durch „Atlanten“ charakterisiert, die angeben, wie ihre lokalen Trivialisierungen „zusammengeklebt“ sind: Sei ${\displaystyle G}$ eine topologische Gruppe, die mittels einer effektiven Wirkung auf der Faser ${\displaystyle F}$ von links wirkt. Ein ${\displaystyle G}$-Atlas des Bündels ${\displaystyle (E,B,\pi ,F)}$ besteht aus lokalen Trivialisierungen, so dass für je zwei überlappende Karten ${\displaystyle (U_{i},\phi _{i})}$ und ${\displaystyle (U_{j},\phi _{j})}$ der Endomorphismus

${\displaystyle \phi _{i}\phi _{j}^{-1}\colon (U_{i}\cap U_{j})\times F\to (U_{i}\cap U_{j})\times F}$

durch

${\displaystyle \phi _{i}\phi _{j}^{-1}(x,\xi )=(x,t_{ij}(x)\xi )}$

gegeben ist, wobei ${\displaystyle t_{ij}\colon U_{i}\cap U_{j}\to G}$ eine stetige Abbildung ist. Zwei ${\displaystyle G}$-Atlanten sind äquivalent, falls ihre Vereinigung ebenfalls ein ${\displaystyle G}$-Atlas ist. Ein ${\displaystyle G}$-Bündel ist ein Faserbündel zusammen mit einer Äquivalenzklasse von ${\displaystyle G}$-Atlanten. Die Gruppe ${\displaystyle G}$ bezeichnet man als die Strukturgruppe des Bündels. Jedes Faserbündel kann durch einen ${\displaystyle G}$-Atlas beschrieben werden, wenn wir die Automorphismengruppe der Faser als Strukturgruppe wählen; wählen wir ${\displaystyle G}$ kleiner, so gewinnt das Faserbündel zusätzliche Struktur.

Weil die Kartenwechsel ${\displaystyle t_{ij}}$ den Übergang zwischen lokalen Trivialisierungen beschreiben, genügen sie der Cozykel-Bedingung ${\displaystyle t_{ik}(x)=t_{ij}(x)t_{jk}(x)}$ (siehe auch Čech-Kohomologie); insbesondere folgen ${\displaystyle t_{ii}(x)=\operatorname {id} _{U_{i}}}$ und ${\displaystyle t_{ij}(x)=t_{ji}(x)^{-1}}$.

Ein Prinzipalbündel ist ein ${\displaystyle G}$-Bündel, bei dem die Faser mit ${\displaystyle G}$ identifiziert wird und auf dem eine Fasern erhaltende Rechts-${\displaystyle G}$-Wirkung auf dem Totalraum erklärt ist.

Literatur

• Norman Steenrod: The Topology of Fibre Bundles. Princeton University Press, Princeton NJ 1951 (Princeton Mathematical Series 14, ISSN 0079-5194), (7. printing, and 1. paperback printing. ebenda 1999, ISBN 0-691-00548-6 (Princeton Landmarks in Mathematics and Physics. = Princeton Paperbacks)).
• David Bleecker: Gauge Theory and Variational Principles. Addison-Wesley publishing, Reading MA 1981, ISBN 0-201-10096-7, Kapitel 1.
• Martin Schottenloher: Geometrie und Symmetrie in der Physik. Leitmotiv der Mathematischen Physik. Vieweg, Braunschweig u. a. 1995, ISBN 3-528-06565-6 (Vieweg-Lehrbuch Mathematische Physik).

Weblinks

• PlanetMath: Fiber Bundle
• MathWorld: Fiber Bundle