Satz von Desargues
Der Satz von Desargues, benannt nach dem französischen Mathematiker Gérard Desargues, ist zusammen mit dem Satz von Pappos einer der Schließungssätze, die für die affine und die projektive Geometrie als Axiome grundlegend sind. Er wird je nach zugrundeliegender Geometrie in einer affinen oder einer projektiven Variante formuliert. In beiden Formen kann der desarguessche aus dem papposschen Satz gefolgert werden. Da es sowohl affine als auch projektive Ebenen gibt, in denen der Satz von Desargues, aber nicht der Satz von Pappos allgemeingültig ist, stellt er eine echte Abschwächung des Satzes von Pappos dar.
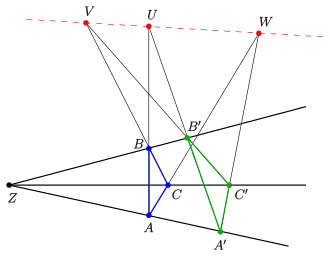
Projektive Form: Wenn sich die Geraden durch zwei sich entsprechende Eckpunkte (siehe Bild) zweier in einer Ebene gelegener Dreiecke und in einem Punkt (dem „Zentrum“) schneiden und die sich entsprechenden verlängerten Seiten sich jeweils in Punkten schneiden, so liegen diese drei Punkte auf einer Geraden (der „Achse“). Die Umkehrung gilt auch.
Projektiv bedeutet hier: alle vorkommenden Geraden schneiden sich, was in einer affinen Ebene nicht der Fall sein muss (siehe affine Form am Ende der Einleitung).
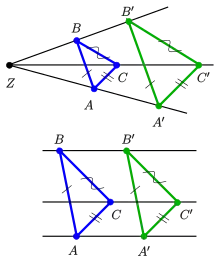
Liegt bei einer Konfiguration das Zentrum auf der Achse , so spricht man vom kleinen Satz von Desargues.
Affine Form: Wenn sich die Geraden durch zwei sich entsprechende Eckpunkte zweier in einer Ebene gelegener Dreiecke in einem Punkt schneiden und zwei Paare korrespondierender Seiten der Dreiecke parallel sind, so ist auch das dritte Paar korrespondierender Seiten parallel.
Die affine Form des kleinen Satzes von Desargues ergibt sich, wenn statt des gemeinsamen Schnittpunkts die Parallelität der Trägergeraden , , vorausgesetzt wird.
Bedeutung für die Synthetische Geometrie
Bei der Klassifikation projektiver Ebenen nach Hanfried Lenz und Adriano Barlotti in der synthetischen Geometrie werden projektive Ebenen formal gruppentheoretisch klassifiziert. Jede Klasse lässt sich aber auch gleichwertig durch eine Spezialisierung des Satzes von Desargues und eine Negation einer anderen Spezialisierung charakterisieren. Die im Folgenden genannten Begriffe bezeichnen Gruppen von Lenz-Barlotti-Klassen, die sich durch die Erfüllung des Satzes von Desargues oder eine seiner Spezialisierungen kennzeichnen lassen:
- Eine affine oder projektive Ebene wird als desarguessche Ebene bezeichnet, wenn die Aussage des (jeweiligen „großen“) Satzes von Desargues allgemeingültig ist. Es gibt auch affine und projektive Ebenen, die nicht desarguessch sind, etwa die Moulton-Ebenen. Sie sind ausgiebig studiert worden, siehe die Bücher von Pickert und Hughes-Piper.
- Eine affine oder projektive Ebene im Sinne der Inzidenzgeometrie ist genau dann eine affine bzw. projektive Ebene im Sinne der linearen Algebra, wenn sie desarguessch ist. Sie lässt sich also genau unter dieser Voraussetzung mithilfe eines zwei- bzw. dreidimensionalen Linksvektorraums über einem Schiefkörper beschreiben. Meist beschränkt man sich in der linearen Algebra auf die Untersuchung der spezielleren papposschen Ebenen, die durch zwei- bzw. dreidimensionale Vektorräume über einem Körper beschrieben werden können.
- Allgemein dienen Ternärkörper (eine Verallgemeinerung der Schiefkörper) zu einer Beschreibung insbesondere der nichtdesargueschen Ebenen durch einen Koordinatenbereich. Hier muss im Allgemeinen keine Spezialisierung des Satzes von Desargues erfüllt sein.
- Als affine Translationsebenen werden affine Ebenen bezeichnet, in denen der kleine affine Satz von Desargues gilt. Sie können mit Hilfe der Gruppe ihrer Parallelverschiebungen, einer Verallgemeinerung des für die affinen Ebenen der linearen Algebra verwendeten Vektorraumkonzepts, untersucht werden. Ihre projektiven Erweiterungen heißen projektive Translationsebenen.
- Eine projektive Ebene, in der der kleine projektive Satz von Desargues allgemeingültig ist, heißt Moufangebene zu Ehren von Ruth Moufang. Durch Ausschneiden einer projektiven Geraden („Schlitzen“) entsteht aus einer Moufang- immer eine affine Translationsebene. Damit lassen sich auch in diesen projektiven Ebenen ähnliche Strukturen wie in affinen Translationsebenen etablieren. Durch projektive Erweiterung einer Translationsebene entsteht allerdings nicht unbedingt eine Moufangebene![1] Insbesondere existieren unendlich viele nichtisomorphe, nichtdesarguessche, endliche Translationsebenen (siehe zum Beispiel Quasikörper#Quasikörper endlicher Moulton-Ebenen), aber jede endliche Moufangebene ist eine Ebene über einem (kommutativen) Körper und daher erst recht desarguessch. Daher kann der projektive Abschluss einer nichtdesarguesschen endlichen Translationsebene nie eine Moufangebene sein.
In mindestens dreidimensionalen affinen und projektiven Räumen gilt der Satz von Desargues immer und ist relativ leicht zu beweisen.[2] Dies ist einer der Gründe, aus denen in der synthetischen Geometrie in der Regel Ebenen besonders intensiv untersucht werden. Siehe dazu auch Axiom von Veblen-Young.
Endliche Ebenen
Die Ordnung einer endlichen affinen Ebene ist die Anzahl der Punkte auf einer (und daher jeder) ihrer Geraden. Welche Ordnungen bei endlichen affinen Ebenen auftreten können, ist ein weitgehend ungelöstes Problem. In endlichen desarguesschen Ebenen (in denen der Satz von Desargues gilt) ist die Ordnung notwendig eine Primzahlpotenz, weil sich in ihnen Koordinaten aus einem endlichen (und daher kommutativen) Körper einführen lassen, und in ihnen gilt automatisch der Satz von Pappos. Zu jeder Primzahlpotenz q existiert eine desarguessche Ebene der Ordnung q. Alle bisher bekannten endlichen affinen Ebenen haben Primzahlpotenzordnung. Die kleinste Ordnung, zu der eine nichtdesarguessche Ebene existiert, ist 9, siehe die Beispiele in Ternärkörper. Ob es affine Ebenen von Nichtprimzahlpotenzordnung gibt, ist ein ungelöstes Problem.
Die Ordnung n ist nicht möglich für n = 6, 14, 21, 22, 30, 33, 42, 46, ...
Wie kommen diese Zahlen zustande? Der Satz von Bruck-Ryser-Chowla sagt folgendes: n lasse bei Division durch 4 den Rest 1 oder 2, sei nicht Summe zweier Quadrate und sei keine Primzahlpotenz (wie in obigen Beispielen). Dann gibt es keine affine Ebene der Ordnung n.
Die Nichtexistenz einer affinen Ebene der Ordnung 10 wurde mit umfangreichem Computereinsatz bewiesen. Für alle hier nicht genannten Ordnungen n, angefangen mit 12, 15, 18, 20, 24, …, ist die Existenzfrage ungelöst.
Literatur
- Albrecht Beutelspacher, Ute Rosenbaum: Projektive Geometrie. Von den Grundlagen bis zu den Anwendungen (= Vieweg Studium: Aufbaukurs Mathematik). 2., durchgesehene und erweiterte Auflage. Vieweg, Wiesbaden 2004, ISBN 3-528-17241-X (Inhaltsverzeichnis).
- Wendelin Degen, Lothar Profke: Grundlagen der affinen und euklidischen Geometrie. Teubner, Stuttgart 1977, ISBN 3-519-02751-8.
- Daniel Hughes, Fred Piper: Projective planes (= Graduate texts in mathematics. Band 6). Springer, Berlin / Heidelberg / New York 1973, ISBN 3-540-90044-6.
- Helmut Karzel, Kay Sörensen, Dirk Windelberg: Einführung in die Geometrie. Vandenhoeck und Ruprecht, Göttingen 1973, ISBN 3-525-03406-7.
- Rolf Lingenberg: Grundlagen der Geometrie I. 3., durchgesehene Auflage. Bibliographisches Institut, Mannheim / Wien / Zürich 1978, ISBN 3-411-01549-7.
- Günter Pickert: Projektive Ebenen. 2. Auflage. Springer, Berlin / Heidelberg / New York 1975, ISBN 3-540-07280-2.
Einzelnachweise
- Günter Pickert: Projektive Ebenen. 2. Auflage. Springer, Berlin / Heidelberg / New York 1975, ISBN 3-540-07280-2.
- Albrecht Beutelspacher, Ute Rosenbaum: Projektive Geometrie. Von den Grundlagen bis zu den Anwendungen (= Vieweg Studium: Aufbaukurs Mathematik). 2., durchgesehene und erweiterte Auflage. Vieweg, Wiesbaden 2004, ISBN 3-528-17241-X, 2.7 Räumliche Geometrien sind desarguessch.