Quantenradierer

Ein Quantenradierer ist ein zentrales Element in quantenphysikalischen Experimenten, mit denen der Doppelcharakter der physikalischen Objekte, mal als ausgedehnte Welle und mal als lokalisiertes Teilchen aufzutreten (Welle-Teilchen-Dualismus), auf besondere Weise verdeutlicht wird. Diese zwei widersprüchlich erscheinenden Aspekte können dabei aber nie gleichzeitig beobachtet werden (Komplementaritätsprinzip).

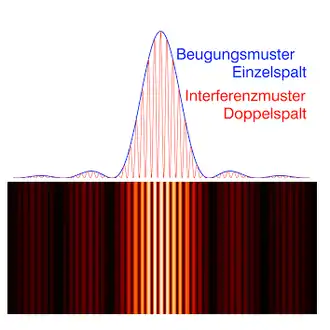
Intensitätsverteilung hinter einem Doppelspalt vor Anbringen einer „Welcher-Weg“-Markierung (rot) bzw. danach (blau). Bei Teilchenstrahlung würde sich nur ein breites zentrales Maximum zeigen.

In dem Experiment wird ein Strahl aus Quantenobjekten (z. B. Photonen, Elektronen, …) auf einen Doppelspalt gerichtet, so dass auf dem Schirm dahinter ein Interferenzmuster entsteht, wie es die Abbildung zeigt. Das Interferenzmuster belegt, dass die Objekte sich nach Art einer Welle bewegen, die aufgrund ihrer Breite durch beide Spalte gleichzeitig hindurch gegangen ist. Sobald aber an einem Spalt dem Zustand der Quantenobjekte beim Passieren eine „Markierung“ aufgeprägt wird, mithilfe derer man erkennen könnte, dass das jeweilige Objekt durch diesen Spalt zum Schirm gelangt ist, entsteht das Interferenzmuster nicht. Stattdessen zeigt sich ein Bild, wie es für klassische Teilchen, die jeweils nur durch einen der Spalte gehen können, zu erwarten ist.

Das klassisch erwartete Bild ohne Interferenzstreifen erscheint nun nicht nur, wenn man die Markierung abliest und dazu nutzt, entweder nur die markierten oder nur die nicht markierten Objekte zu zählen. Denn schon die Erzeugung einer solchen „Welcher-Weg“-Markierung, auch wenn sie gar nicht abgelesen wird, zerstört das Interferenzmuster. Dies ist für Licht, also auch für die einzelnen Photonen, schon lange bekannt. Neuartig am Quantenradierer ist die Beobachtung, dass man das Interferenzmuster wieder herstellen kann, indem man die schon angebrachte Markierung wieder auslöscht („wegradiert“). Dabei kann sogar mit einem späten Ein- oder Ausschalten des Quantenradierers scheinbar nachträglich entschieden werden, ob das Quantenobjekt vorher als Welle durch beide Spalte oder als Teilchen nur durch einen Spalt gegangen ist („Delayed-Choice-Experiment“).

Das Experiment hat innerhalb und außerhalb der Physik Aufmerksamkeit erregt,[1] deckt aber keine neuartigen Eigenschaften der Quantenobjekte auf. Insbesondere überschreitet es nicht den Rahmen der verbreiteten Kopenhagener Deutung der Quantenmechanik, sondern ist bei sorgfältiger Formulierung vollständig mit den bekannten Regeln der Quantenmechanik zu erklären. Der Quantenradierer widerlegt die vereinfachte Vorstellung vom Welle-Teilchen-Dualismus, nach der das Quantenobjekt schon beim Passieren des Doppelspalts darauf festgelegt würde, entweder als Welle gleichzeitig durch beide Spalte oder als Teilchen immer nur durch einen der Spalte zu gehen. In dem Bestreben, diese Sichtweise beizubehalten, gehen manche Vorschläge zur Interpretation so weit, auch eine Rückwärtsverursachung (englisch backward causation oder retrocausality), also eine Umkehrung der zeitlichen Abfolge von Ursache und Wirkung, in Erwägung zu ziehen[2][3][4] oder sogar als erwiesen zu erachten.[5]

Der Quantenradierer wurde 1982 als Gedankenexperiment vorgeschlagen,[6] realisiert worden ist er erstmals 1991 für Photonen.[7] Heute kann er auch im Physikunterricht an der Schule gezeigt werden.[8][9] Für Elektronen wurde der Quantenradierer 2014 realisiert.[10] Für Atomstrahlen wurde das Verschwinden der Interferenzstreifen durch das Anbringen einer Markierung erstmals 1998 experimentell demonstriert,[11] die Realisierung eines Quantenradierers steht hier noch aus.

Überblick über das Experiment

Das typische Experiment mit dem Quantenradierer besteht aus drei Schritten[12]:

Durch einen kohärent beleuchteten Doppelspalt wird auf einem Schirm das charakteristische Interferenzmuster hervorgerufen: ein breiter heller Streifen, der durch mehrere dunkle Interferenzstreifen unterbrochen ist. Die Strahlung kann Licht sein, also aus Photonen bestehen, oder aus anderen Quantenobjekten wie Elektronen, Neutronen, ganzen Atomen usw. Das Streifenmuster entsteht, weil sich die zwei aus den einzelnen Spalten austretenden Strahlungsfelder überlagern. Lässt man nämlich die Strahlung nur durch einen der Spalte hindurch, ist das Interferenzmuster zu einem einheitlich hellen Streifen verwischt. Die Interferenzstreifen beweisen den Wellencharakter der Strahlung, denn ohne dass ein ausgedehntes Wellenfeld durch beide Spalte gleichzeitig hindurchgegangen ist, kann zum Beispiel die gegenseitige Auslöschung nicht eintreten, die die dunklen Streifen erklärt. Mit klassischen Teilchenstrahlen würde man einen einheitlich hellen Streifen (genauer: zwei überlappende helle Streifen) auch dann erhalten, wenn beide Spalte offen sind.
Im nächsten Schritt wird für jedes der den Doppelspalt passierenden Objekte eine „Welcher-Weg“-Markierung erzeugt und irgendwo in der Apparatur gespeichert, ohne dass die weitere Ausbreitung der Strahlung beeinflusst wird. Die Markierung ist eine physikalische Eigenschaft, mit deren Hilfe man von jedem der auf dem Schirm auftreffenden Objekte entscheiden könnte, durch welchen der beiden Spalte es gekommen ist. Damit kann man das Experiment z. B. dahingehend abändern, dass unter den Treffern auf dem Schirm nur diejenigen registriert werden, die zum Durchgang des Quants durch einen bestimmten Spalt gehören. Als Ergebnis würde in diesem Fall dasselbe Bild entstehen, als ob man den anderen Spalt geschlossen gehalten hätte: ein breiter heller Streifen ohne die dunklen Interferenzstreifen darin, als ob diese übermalt worden wären. Doch überraschenderweise entsteht dasselbe verwaschene Bild (also ohne Interferenzstreifen) auch dann, wenn man am Schirm die Welcher-Weg-Markierung gar nicht beachtet, also alle auftreffende Strahlung registriert, unabhängig davon, welche Markierung sie hat. Dieses Bild wäre aber zu erwarten, wenn die Quantenobjekte nicht beide Spalte gleichzeitig, sondern tatsächlich nur wie klassische Teilchen entweder den einen oder den anderen Spalt passiert hätten. Da aber beide Spalte offen sind, ist zu folgern, dass schon nach dem Speichern der Markierung die Strahlungsfelder aus den beiden Spalten einander nicht mehr auslöschen können, obwohl sie sonst unverändert sind. Der einzige Grund kann das Vorhandensein dieser Welcher-Weg-Markierung sein. Es scheint, dass das bloße Erzeugen der Markierung eine Verwandlung der vorher wellenartigen Quanten der Strahlung in teilchenartige bewirkt hat. Es ist aber anzumerken, dass das so entstandene Muster immer noch Merkmale von Interferenz aufweist. Sie zeigen sich seitlich am Rand des breiten verwaschenen Streifens, wo schwach ausgeprägte Interferenzstreifen erscheinen, die von der Beugung der Wellen an jedem Spalt einzeln hervorgerufen werden (siehe in der Abbildung oben die blaue Kurve "Beugungsmuster Einzelspalt", oder den Abschnitt zum Interferenzmuster im Artikel Doppelspaltexperiment). Genau gesagt geht es hier also nicht um Verlust und Wiederherstellung der Interferenzfähigkeit der Strahlung ganz allgemein, sondern nur in Bezug auf die Interferenzfähigkeit der beiden Strahlungsfelder aus den einzelnen Spalten.
Im letzten Schritt durchläuft nun das gesamte Strahlungsfeld aus beiden Spalten, bevor es auf dem Schirm registriert wird, den Quantenradierer. Dieser entfernt die den einzelnen Strahlungsquanten zugeordneten „Welcher-Weg“-Markierungen so gründlich, dass es danach ganz prinzipiell keine physikalische Möglichkeit mehr gibt, die am Schirm eintreffenden Quantenobjekte noch dem einen oder anderen Spalt zuzuordnen. Dann entsteht das durch die „Welcher-Weg“-Markierung vorher zerstörte, für Wellen charakteristische Interferenzbild von neuem. Gewissermaßen wird die vom Vorhandensein der „Welcher-Weg“-Markierung ausgelöste Übermalung des Interferenzbilds „wegradiert“.

Dieses Verhalten erscheint vor allem dann paradox, wenn es so dargestellt wird, als sei die mit dem Strahlungsfeld transportierte Information, die im 1. Schritt das Interferenzmuster entstehen lässt, im 2. Schritt durch die Welcher-Weg-Markierung erst unwiederbringlich verlorengegangen und nun im 3. Schritt durch den Quantenradierer wieder hergestellt worden. Besonders erstaunlich muss es dann erscheinen, dass es genügt, für jedes Objekt den Quantenradierer erst nach dem Passieren des Doppelspalts überhaupt einzuschalten („Delayed-Choice-Experiment“). Man kann das ursprüngliche Interferenzmuster sogar auch dann noch aus der gesamten Strahlung herausfiltern, wenn alle Quantenobjekte auf dem Schirm schon registriert wurden und dann erst der Quantenradierer die (anderswo gespeicherte) Welcher-Weg-Markierung „wegradiert“.

Quantenradierer für Photonen

Der Quantenradierer für Photonen kann relativ einfach aufgebaut werden, so dass er auch zunehmend in Physik-Schulbüchern und Lehrplänen angesprochen wird.[8][9] Er lässt sich schon mit der klassischen Wellenvorstellung des Lichts erklären, denn diese gibt das durchschnittliche Verhalten von Photonen richtig wieder.

In seiner einfachsten Form arbeitet der Quantenradierer mit linear polarisierten Photonen. Es wird die Tatsache ausgenutzt, dass zwei ansonsten kohärente Wellen sich nicht auslöschen oder auf andere Weise destruktiv interferieren können, wenn ihre Polarisationsebenen senkrecht zueinander stehen. Ausgangspunkt ist das Doppelspaltexperiment mit einer unpolarisierten monochromatischen Lichtquelle, die auf dem Schirm das typische Muster von hellen und dunklen Interferenzstreifen erzeugt. Bringt man vor (oder hinter) den beiden Spalten je einen Polarisationsfilter an, so verschwinden die Interferenzstreifen, wenn die beiden Filter unter 90° zueinander verdreht sind, also z. B. horizontal und vertikal. Der Schirm zeigt dann einen einheitlichen breiten Streifen, wie er von jedem Spalt einzeln erzeugt würde, wenn der andere Spalt verschlossen ist. Um die Interferenzstreifen wieder erscheinen zu lassen, filtert man vor dem Schirm das ganze ankommende Licht noch einmal mit einem dritten Polarisationsfilter, der unter 45° („schräg nach rechts oben“) zu den beiden anderen steht. Hierfür gibt es zwei mögliche Positionen, die ihrerseits um 90° gegeneinander verdreht sind („schräg nach rechts“ bzw. „nach links“ oben). Für eine dieser beiden Positionen entsteht auf dem Schirm genau dasselbe Interferenzmuster wie ohne Markierung der Quanten, wenn auch nur mit halbierter Intensität. Der so positionierte dritte Filter ist der Quantenradierer.

In der bei Quantenradierern gebräuchlichen Terminologie wird jeder der beiden Teilwellen, wenn sie ihren Polarisationsfilter durchläuft, die jeweilige Welcher-Weg-Information aufgeprägt. Auf den Schirm trifft dann die kohärente Überlagerung von horizontal und vertikal polarisierten Wellen, die sich nun nicht mehr auslöschen können. Durch den dritten Filter, den sie beide durchlaufen, wird die Information über den Weg wieder gelöscht („ausradiert“), denn für beide Teilwellen haben die Komponenten, die diesen Filter passieren, die gleiche Polarisationsrichtung und bei der Filterstellung ±45° auch gleiche Amplitude. Allerdings wird sowohl beim Aufprägen der Welcher-Weg-Markierung als auch beim Wegradieren jeweils die Intensität halbiert. Nach dem letzten Filter bleiben damit nur diejenigen Komponenten der ursprünglichen Wellen übrig, die eigens ausgewählt wurden, um das ursprüngliche Interferenzmuster wieder erstehen zu lassen. Die in diesen Komponenten vorhandene Information ist also nie gelöscht und daher auch nicht wiederhergestellt worden. Sie war nur verdeckt von den anderen Komponenten, die im letzten Polarisationsfilter absorbiert worden sind. Diese kann man auch für sich allein sichtbar machen, indem man für den letzten Filter die andere der beiden schräg orientierten Richtungen auswählt. Dann ist der Filter auch wieder genau zwischen den beiden Richtungen der Welcher-Weg-Markierung orientiert und lässt infolgedessen ein voll interferenzfähiges Strahlungsfeld passieren. Dieses erzeugt ein Interferenzmuster, das an derselben Stelle liegt wie das erste und auch genau so aussieht, aber mit den hellen und dunklen Interferenzstreifen gegeneinander vertauscht. Die Streifen liegen in den beiden Interferenzbildern also auf Lücke. Bevor der dritte Polarisationsfilter eingefügt wurde, waren diese beiden Strahlungsfelder vereint auf den Schirm gefallen. Der dabei beobachtete einheitliche breite Streifen, vorher als inkohärente Überlagerung der horizontal und vertikal polarisierten Teilwellen aus je einem Spalt interpretiert, wird in dieser Beschreibung also – und genau so richtig – als die inkohärente Überlagerung von zwei komplementären Interferenzbildern des Doppelspalts interpretiert. Beide Beschreibungen desselben Strahlungsfeldes (mit Bestandteilen, die entweder horizontal bzw. vertikal oder aber „schräg nach rechts“ bzw. „nach links“ polarisiert sind) sind physikalisch ununterscheidbar und daher in jeder Hinsicht äquivalent.

Da sich das gleiche Ergebnis immer noch zeigt, wenn die Lichtquelle soweit abgeschwächt wird, dass immer nur ein Photon zur Zeit durch die Apparatur fliegt, muss man den ganzen Vorgang auch anhand eines einzelnen Photons beschreiben können. Das macht zunächst keine Schwierigkeiten, denn die quantenmechanische Amplitude eines Photons verhält sich genau wie eine elektromagnetische Welle nach den Maxwell-Gleichungen. Aber der Vorgang der Aufprägung der Welcher-Weg-Information muss sorgfältig formuliert werden. Denn im Gegensatz zu häufigen Darstellungen kann man hier nicht sagen, ein Polarisationsfilter würde die Polarisation des einzelnen Photons messen oder festlegen.[13] Das würde nämlich bedeuten, dass das Photon als Ganzes im Sinne einer quantenmechanischen Messung auf einen der beiden Eigenzustände parallel bzw. senkrecht zur Orientierung des Filters festgelegt wird. Wenn das einfallende Photon im Eigenzustand parallel zur Polarisationsrichtung ist, kommt es ungeändert durch. Bei beliebig gedrehter Polarisationsrichtung kommt das Photon aber nur mit der Feldkomponente durch, die zur Polarisationsrichtung parallel ist. Der andere Anteil, also die dazu senkrechte Feldkomponente, verschwindet aber nicht durch die Zustandsreduktion, wie es bei einer quantenmechanischen Messung sein müsste. Vielmehr wird er durch eine echte physikalische Wechselwirkung mit dem Material des Filters (z. B. Reflexion) am Passieren des Filters gehindert. Damit hat die hindurchgelassene Feldkomponente dann nicht die volle Amplitude, die zu einem ganzen Photon gehören würde, was ebenfalls im Widerspruch zum Ergebnis einer Zustandsreduktion steht. Die reduzierte Amplitude zeigt sich unter anderem dann, wenn auf einem Schirm direkt hinter dem Filter schließlich eine wirkliche Messung des Photons erfolgt: dort gibt das Quadrat dieser Amplitude die Wahrscheinlichkeit an, dass das Photon angekommen ist. Für die korrekte Darstellung des Quantenradierers ist festzuhalten, dass man von dem Photon nach Passieren des Doppelspalts und der Aufprägung der Welcher-Weg-Markierung weder sagen kann, es sein durch einen bestimmten Spalt gegangen, noch, es habe eine bestimmte Polarisation erhalten. Vielmehr befindet sich das Photon in einem kohärenten Überlagerungszustand aus zwei Komponenten, die den beiden möglichen Wegen und zugehörigen Markierungen entsprechen.

Zu beachten ist auch, dass die Unterscheidung zwischen dem Erscheinen und dem Nichterscheinen eines Interferenzbilds nicht schon durch die Beobachtung eines einzelnen Photons auf dem Schirm getroffen werden kann. Das ist erst anhand der Helligkeitsverteilung möglich, die sich nach Auftreffen vieler Photonen auf dem Schirm zeigt. Jedoch sagt auch dieser Unterschied nichts darüber aus, ob die einzelnen Photonen sich als Welle oder Teilchen verhalten haben. Denn eine Überlagerung von Wellen, die nicht interferenzfähig sind, ist von einem Bündel von Teilchenstrahlen nicht zu unterscheiden, wie sich z. B. an dem nützlichen Konzept der Lichtstrahlen erweist. Daher ist aus der Abwesenheit von Interferenzstreifen nicht zu schließen, dass die Photonen Teilchen sind, denn auch eine inkohärente Überlagerung von Wellen ist damit nicht ausgeschlossen.

Quantenradierer mit einem Paar verschränkter Photonen

Der Quantenradierer funktioniert auch dann, wenn er gar nicht auf das durch den Doppelspalt fliegende Photon wirkt (das hier traditionell mit s bezeichnet wird), sondern auf ein anderes Photon i, das zwar an der Blende mit dem Doppelspalt vorbeifliegt, mit Photon s aber hinsichtlich der Polarisation quantenmechanisch verschränkt ist. Aufgrund der Verschränkung lässt eine Messung an i durch die damit ausgelöste Zustandsreduktion auch das Photon s in der Zustandskomponente zurück, die mit dem an i festgestellten Zustand verschränkt war. (Die damit verbundenen begrifflichen Probleme bilden das Einstein-Podolsky-Rosen-Paradoxon.)

Quantenradierer mit verschränkten Photonen

In dem von Stephen Walborn und anderen an der brasilianischen Universidade Federal de Minas Gerais im Jahr 2001 durchgeführten Experiment[14] (siehe Abb.) werden zuerst durch parametrische Fluoreszenz (engl. Spontaneous parametric down-conversion, SPDC) in einem geeignet orientierten BBO-Kristall solche verschränkten Photonenpaare erzeugt, allerdings mit extrem geringer Wahrscheinlichkeit. Von den beiden Photonen, die in verschiedene Richtungen fliegen, ist eins horizontal und das andere vertikal polarisiert. In Bezug auf die Polarisation gehört zu dem Zustand die 2-Photonen-Wellenfunktion

\Psi _{H,V}=H_{s}\;V_{i}+V_{s}\;H_{i}

,

wobei $H$ und $V$ für die Polarisationsrichtungen eines einzelnen Photons stehen und der Index das jeweilige Photon angibt[15].

Der BBO-Kristall wird so platziert, dass nur eins der beiden verschränkten Photonen (mit s bezeichnet) den Doppelspalt passiert. Danach besteht das s-Photon aus den zwei Teilwellen aus den jeweiligen Spalten, die miteinander infererieren und auf dem Schirm das Streifenmuster erzeugen. Allerdings muss, zwecks nachträglicher Auswahl der nachgewiesenen Photonen, der Schirm hier durch einen elektronischen Zähler ersetzt werden, der außer dem Ort auch die Zeit des Eintreffens des Photons misst. Um diese Interferenz zu zerstören, wird durch zwei um $\pm 45^{o}$ gegen die Vertikale verdrehte Lambda-Viertel-Plättchen, je eines direkt hinter jedem Spalt, eine Welcher-Weg-Markierung in Gestalt einer rechts bzw. links orientierten Zirkularpolarisation erzeugt. Je nach Winkelabstand von $+45^{o}$ bzw. $-45^{o}$ wird die $V_{s}$ -Komponente verlustlos in eine solche rechts- bzw. linkszirkularpolarisierte Welle umgeformt. Diese beiden Teilwellen überlagern sich zwar genauso wie vorher, sie können einander aber aufgrund ihrer entgegengesetzten Zirkularpolarisation nicht mehr auslöschen. Das gleiche passiert mit der horizontal polarisierten Komponente $H_{s}$ , nur mit umgekehrter Zuordnung von rechts und links-Polarisation. Die Zustände von Photon i, mit denen diese beiden Komponenten $H_{s}$ und $V_{s}$ von Photon s durch die Verschränkung verknüpft sind, sind voneinander verschieden (nämlich $V_{i}$ bzw. $H_{i}$ ), daher können auch $H_{s}$ und $V_{s}$ nicht miteinander interferieren. Es entsteht auf dem Schirm die inkohärente Summe aller vier genannten Teilwellen, also ein Bild ohne Interferenzstreifen.

Der Quantenradierer, der gar nicht direkt auf das s-Photon einwirkt, ist nun einfach auf dem Weg des i-Photons ein um 45° gegen die Vertikale verdrehter Polarisationsfilter mit einem elektronischen Zähler dahinter. Der Filter unterscheidet zwischen den schräg um $\pm 45^{o}$ polarisierten Zuständen, die durch die symmetrische bzw. antisymmetrische Linearkombination

\Phi _{i\pm }=H_{i}\pm V_{i}

definiert sind. Eine kommt durch, die andere nicht. Dieses sind zwei Basiszustände, mit deren Linearkombinationen man alle ankommenden i-Photonen beschreiben kann. Wenn der Zähler anspricht und die entsprechende Zustandsreduktion auslöst, steht fest, dass er ein Photon i im richtigen Polarisationszustand gezählt hat, also z. B. immer nur in der antisymmetrischen Linearkombination $\Phi _{i-}$ . Zählt man (durch eine Koinzidenzschaltung) nur die zusammengehörigen Treffer von Photon s und Photon i in ihrem jeweiligen Detektor, dann hat man nur diejenigen Photonen s mitgezählt, deren Partnerphoton durch $\Phi _{i-}$ gegeben ist. Die Auftrefforte dieser s-Photonen kann man zu einem beliebigen späteren Zeitpunkt aus der Gesamtheit aller s-Photonen herausfiltern, wenn man zu jedem von ihnen gespeichert hat, ob gleichzeitig ein i-Photon nachgewiesen wurde. Um diese Photonen näher zu betrachten, drückt man im ursprünglichen 2-Photonen-Zustand $\Psi _{s,i}$ die Zustände des i-Photons durch $\Phi _{i\pm }$ aus. Dann zeigt sich, dass die gesamte Wellenfunktion der 2-Photonen-Polarisation auch so geschrieben werden kann[15]:

\Psi _{+,-}=\Phi _{s+}\,\Phi _{i-}+\Phi _{s-}\;\Phi _{i+}

.

$\Phi _{i-}$ ist also mit der Komponente

\Phi _{s+}=H_{s}+V_{s}

des s-Photons verknüpft, und entsprechend $\Phi _{i+}$ mit

\Phi _{s-}=H_{s}-V_{s}

.

Die Wellenfunktion $\Psi _{+,-}$ sieht zwar ganz anders aus als $\Psi _{H,V}$ , beide sind aber mathematisch identisch[15] und beschreiben ein und denselben physikalischen Zustand. Nur die Komponenten sind anders zusammengefasst. Daran wird deutlich, dass es keine sinnvolle Fragestellung ist, ob die Photonen als $H$ und $V$ erzeugt und dann in verschiedene Richtungen geflogen sind, oder als $\Phi _{\pm }=H\pm V$ erzeugt und sich jedes in beide Richtungen gleichzeitig ausbreitet. Beides ist physikalisch nicht zu unterscheiden und daher gleichzeitig richtig. Je nach Detektor können die Eigenzustände der nachfolgenden Messung an einem der Photonen $\Phi _{+}$ und $\Phi _{+}$ sein, oder aber $H$ und $V$ . Dann eignet sich die eine oder die andere Darstellung besser, die Folgen der Zustandsreduktion darzustellen. Es wird in jedem Fall bei der ersten irreversiblen Messung genau der Summand von $\Psi _{+,-}$ bzw. $\Psi _{H,V}$ durch eine Zustandsreduktion gelöscht, auf den der Detektor nicht empfindlich ist, und im übriggebliebenen Summanden ist mit dem Zustand des ersten nachgewiesenen Photons dann auch der des anderen Photons festgelegt, ganz gleich, welches Photon zeitlich als erstes beobachtet wurde und wann und wo das zweite beobachtet wird.

Nachdem beispielsweise die schräg polarisierte $\Phi _{i-}$ -Komponente des i-Photons den Zähler ausgelöst hat, eine womöglich vorher vorhandene $\Phi _{i+}$ -Komponente also der Zustandsreduktion zum Opfer gefallen ist, ist auch von dem s-Photon nur noch die zu $\Phi _{i-}$ gehörige Komponente $\Phi _{s+}$ übrig. Diese ist entweder unter $+45^{o}$ oder $-45^{o}$ polarisiert und wird daher von beiden Lambda-Viertel-Plättchen ungeändert hindurchgelassen, so dass sie auf dem Schirm (bzw. im ortsempfindlichen Detektor) das ursprüngliche Interferenzmuster erzeugt. Im Endeffekt scheint also die Welcher-Weg-Markierung gelöscht worden zu sein. Genauer ausgedrückt: sie ist nicht gelöscht, sondern war den am Ende durchgekommenen Komponenten gar nicht aufgeprägt worden.

Würde man aber den i-Detektor ausschließlich für die symmetrische Komponente $\Phi _{i+}$ empfindlich machen, was durch einfaches Drehen des davor angebrachten Polarisationsfilters um 90° erreicht werden kann, dann bliebe von den mit diesen i koinzidenten s-Photonen die antisymmetrische Komponente $\Phi _{s-}$ übrig. Sie geht auch ungeändert durch die Lambda-Viertel-Plättchen und würde ein Interferenzbild erzeugen, dem ersten exakt gleich, nur dass die hellen und dunklen Streifen miteinander vertauscht sind.

Quantenradierer mit zwei Paaren verschränkter Photonen

In einem viel zitierten Experiment[16] wurde der BBO-Kristall erst hinter dem Doppelspalt platziert, so dass für jede der beiden austretenden Teilwellen $\Phi _{1},\;\Phi _{2}$ die Wahrscheinlichkeit besteht, ein verschränktes Photonenpaar zu erzeugen. In dem Wellenfeld aus diesen vier Photonen (s₁, i₁ für den einen Spalt und s₂, i₂ für den anderen) können wegen der Energieerhaltung immer nur zwei real nachgewiesen werden, aber bis zum Nachweis können sie alle vier (mit reduzierter Amplitude) in der Gesamtwellenfunktion vorkommen. Darin sind je zwei Photonen mit gleichem Index hinsichtlich der vertikalen bzw. horizontalen Polarisation verschränkt, während zwischen je zwei Photonen mit verschiedenem Index die richtungsabhängige Phasenbeziehung gilt, die für die Doppelspaltinterferenz typisch ist. Die mit mehreren Detektoren ausgestattete Apparatur ist so justiert, dass eins der Photonen aus jedem Paar (i₁ und i₂) durch seine Flugrichtung identifizierbar ist, während sich die Wellenfelder der beiden andern (s₁ und s₂) zu s₁+s₂ überlagern können. s₁ und s₂ erzeugen also, wenn sie gleich polarisiert sind, das Interferenzmuster des Doppelspalts, das mit einem ortsempfindlichen Detektor im Überlagerungsgebiet nachgewiesen werden kann. Spricht nun z. B. der zuständige Detektor auf ein Photon i₁ an, dann steht fest, dass dazu ein s₁ wirklich erzeugt worden ist, aber keins der Photonen mit Index 2. Diese kamen als Komponenten der Wellenfunktion noch vor, sind aber durch die Zustandsreduktion gelöscht worden. Dann kann es kein Interferenzmuster geben. Zwei weitere Detektoren sind auf die Überlagerung i₁+i₂ bzw. i₁-i₂ empfindlich, die mithilfe der teilweisen Reflexion an halbdurchlässigen Spiegeln für einen Teil der Gesamtintensität mit gewisser Wahrscheinlichkeit fortlaufend herbeigeführt wird. Die damit verschränkten s-Photonen befinden sich dann auch im Überlagerungszustand s₁+s₂ bzw. s₁-s₂. Daher erzeugen sie im ortsempfindlichen Detektor das originale Interferenzmuster des Doppelspalts bzw. dessen Gegenstück mit vertauschten hellen und dunklen Streifen. Im wirklichen Experiment kann man den Photonen keine dieser Alternativen vorschreiben. Es wird stattdessen die Intensität des einfallenden Lichts so weit gedrosselt, dass nur die Ereignisse abgespeichert werden, bei denen der s-Detektor und einer der drei i-Detektoren ein Signal gegeben hat, die ursprünglich alle von einem einzigen auf den Doppelspalt einfallenden Photon stammen müssen. Je nachdem, welcher i-Detektor das war, zeigen die s-Signale das originale oder das invertierte Interferenzmuster oder aber das Muster ohne Interferenz. Im ersten Fall hat sich der Wellencharakter der ursprünglich einfallenden Photonen gezeigt, im zweiten der Teilchencharakter.

Es handelt sich also um statistische Korrelationen zwischen s- und i-Detektoren, bei denen es prinzipiell nicht auf die genaue zeitliche Reihenfolge der Signale ankommt. Daher sind auch keine Unterscheidungen von Ursache und Wirkung möglich (obwohl zur leichteren Darstellung des Vorgangs oben eine bestimmte Abfolge angenommen wurde). Daher hat das Experiment das gleiche Ergebnis, wenn der i-Detektor erst deutlich nach dem s-Detektor erreicht wurde. Spekulationen hinsichtlich einer Möglichkeit, dass das spätere Signal des i-Detektors noch das frühere Verhalten der s-Photonen beeinflussen könnte, sind daher abwegig.

Der Vorgang im Einzelnen

Warum verschwindet das Interferenzmuster?

Ein „Welcher-Weg“-Detektor, mit dessen Hilfe man den Weg eines Quantenobjekts bestimmen könnte, schließt dieses von der Möglichkeit der Interferenz aus. Man beobachtet also aufgrund der bloßen Möglichkeit, die Welcher-Weg-Information zu gewinnen – auch wenn sie gar nicht ausgelesen wird – statt Interferenzstreifen eine Häufigkeitsverteilung in Form eines verwaschenen Streifens.[17] Allerdings ist es bei näherer Analyse nicht die räumliche Bedeutung der Welcher-Weg-Information, die die Interferenz verhindert, sondern der Umstand, dass das Quantenobjekt bei deren Aufprägen eine messbare Veränderung durchmacht (die aber die räumliche Ausbreitung unverändert lässt). Das Quantenobjekt (oder ein anderes Objekt in der Apparatur) muss nämlich in einen je nach Weg physikalisch unterscheidbaren Zustand versetzt werden (oder man muss aus dem ankommenden Quantenobjekt physikalisch unterscheidbare Komponenten herausfiltern). Beim Quantenradierer mit Photonen (auch mit Neutronen oder Elektronen) ist das der verschiedene Polarisationszustand, es kann aber auch jede andere Art von innerem Freiheitsgrad genutzt werden. Sind die Quantenobjekte z. B. ganze Atome, kann die Unterscheidungsmöglichkeit durch die Anregung zu einem anderen inneren Zustand geschaffen werden[11] oder durch Hinterlassen eines Mikrowellenphotons in einem kleinen Hohlraumresonator vor einem der Spalte. Da Quantenobjekte in orthogonalen (d. h. messbar verschiedenen) inneren Zuständen (oder verschränkt mit zwei solchen Zuständen eines anderen Objekts) nicht interferenzfähig sind, überlagern sich ihre Wege inkohärent, so dass die resultierende Häufigkeitsverteilung dieselbe wird wie bei Teilchenstrahlen.

Dieser Zusammenhang kann mithilfe der Wellenfunktion $\Psi ({\vec {r}},s)$ des Quantenobjekts im Einzelnen dargestellt werden, wobei hier der Fall einer Markierung in Form eines inneren Zustands angenommen ist.[7] Dabei steht ${\vec {r}}$ für die Ortsvariable und $s$ abgekürzt für alle inneren (d. h. vom Ort des Quantenobjekts unabhängigen) Variablen. Zu Beginn hat die Wellenfunktion die einfache Produktform

\Psi ({\vec {r}},s)=\Phi ({\vec {r}})\,\chi (s)

,

wobei die $\Phi ({\vec {r}})$ den Ortszustand angibt, also die Amplitude der Aufenthaltswahrscheinlichkeit am Ort ${\vec {r}}$ . Entsprechend ist $\chi (s)$ die Wahrscheinlichkeitsamplitude dafür, dass die inneren Variablen den Wert $s$ haben. Nach Passieren des Doppelspalts ist der innere Zustand zunächst ungeändert, aber die Ortswellenfunktion ist nun die kohärente der durch die beiden Spalte erzeugten Teilwellen:

\Psi ({\vec {r}},s)=\left(\Phi _{1}({\vec {r}})+\Phi _{2}({\vec {r}})\right)\chi (s)

Das Absolutquadrat dieser Summe ist auf dem Schirm nicht überall gleich groß, sondern variiert mit dem ortsabhängigen Weglängenunterschied der beiden Teilwellen $\Phi _{1}({\vec {r}}),\;\Phi _{2}({\vec {r}})$ . Es hat überall den Wert null, wo der Weglängenunterschied eine halbe Wellenlänge beträgt, was gerade die dunklen Interferenzstreifen hervorruft. Folglich hat hier auch die ganze Wellenfunktion $\Psi ({\vec {r}},s)$ für das Quantenobjekt den Wert null. Da die Wahrscheinlichkeitsdichte für das ganze Quantenobjekt für beliebigen Ort ${\vec {r}}$ durch

\left|\Psi ({\vec {r}},s)\right|^{2}=\left|\left(\Phi _{1}({\vec {r}})+\Phi _{2}({\vec {r}})\right)\right|^{2}\;\left|\chi (s)\right|^{2}

gegeben ist, kann es nicht an Orten sein, wo allein die Summe der Ortsfunktionen null ist, und zwar unabhängig von seinem inneren Zustand.

Wenn jetzt die Welcher-Weg-Markierung aufgeprägt wird, müssen die Teilwellen $\Phi _{1,2}$ mit verschiedenen inneren Zuständen verknüpft werden. Diese Zustände, hier $\chi _{1,2}$ genannt, müssen physikalisch – also in einem einer Messung zugänglichen Messwert – unterscheidbar sein, und sind daher orthogonal. Bei Experimenten mit Photonen wählt man lineare Polarisation in zwei zueinander senkrechten Richtungen, bei Experimenten mit Atomen wählt man für eine der Teilwellen die Anregung eines inneren Zustands des Atoms, z. B. Anregung in einen anderen Zustand der Hyperfeinwechselwirkung. Die ganze Wellenfunktion heißt dann

\Psi ({\vec {r}},s)=\Phi _{1}({\vec {r}})\,\chi _{1}(s)+\Phi _{2}({\vec {r}})\,\chi _{2}(s)

,

und ein Zusammenfassen der Ortswellenfunktionen in einer kohärenten Summe ist nicht mehr möglich. Dies ist ein Beispiel für die Quantenverschränkung der Ortsvariable mit den inneren Variablen. Diese gesamte Wellenfunktion ist immer noch eine kohärente Summe der Beiträge, die aus den beiden einzelnen Spalten hervorgegangen sind. Daher enthält die Wahrscheinlichkeitsdichte $\left|\Psi ({\vec {r}},s)\right|^{2}$ außer der inkohärenten Summe der beiden Dichten für die einzelnen Teilwellen zwei Interferenzglieder von der Form

\Phi _{1}({\vec {r}})^{*}\,\Phi _{2}({\vec {r}})\,\chi _{1}(s)^{*}\,\chi _{2}(s)

.

Doch weil der innere Zustand gar nicht gemessen wird, muss über die innere Variable $s$ summiert werden. Und weil $\chi _{1}$ und $\chi _{2}$ orthogonale Zustände sind, ergibt jedes Interferenzglied dabei einzeln den Wert null. Übrig bleibt die Wahrscheinlichkeitsdichte

\sum _{s}\left|\Psi ({\vec {r}},s)\right|^{2}=\left|\Phi _{1}({\vec {r}})\right|^{2}+\left|\Phi _{2}({\vec {r}})\right|^{2}

,

eben die inkohärente Summe der räumlichen Intensitäten der beiden Teilwellen. Obwohl die inneren Freiheitsgrade gar nicht gemessen werden, hat allein die Tatsache, dass es sich um zwei messbar unterscheidbare innere Zustände handelt, Einfluss auf das Endergebnis.

In einem Experiment mit Atomstrahlen[11] ist im Jahr 1998 das Verschwinden der Interferenz dadurch ausgelöst worden, dass an einem Spalt die Atome mit etwa 1μeV zu einem anderen Hyperfeinniveau angeregt wurden, eine Markierung, die beim Aufprägen praktisch keinen Einfluss auf die räumliche Bahn der Atome hatte. Nach dem Doppelspalt hatten die Atome also einen von zwei orthogonalen inneren Zuständen, was trotz der extrem geringen Anregungsenergie den Verlust der Interferenzfähigkeit bewirkte. Eine andere Form der Welcher-Weg-Markierung von Atomen wurde 1991 vorgeschlagen[7], blieb aber bisher ein Gedankenexperiment: Hier wird die Welcher-Weg-Markierung nicht von dem Atom selbst mitgenommen, sondern in Form der Anregung eines von zwei Mikrowellenresonatoren gespeichert, die nebeneinander vor den beiden Spalten stehen und von jedem Atom gleichzeitig durchflogen werden. Jedes Atom war vorher angeregt worden und gibt mit Sicherheit die Anregungsenergie dort ab. Es wurde diskutiert[18][19][20], ob mit dieser Energieabgabe nicht doch eine unkontrollierbare Änderung des Impulszustands des Atoms einhergeht, die für sich schon die Bildung eines stabilen Interferenzmusters verhindern würde.

Warum erscheint das Interferenzmuster wieder?

Aus den vorstehenden Formeln geht hervor, dass das Interferenzmuster wieder entsteht, wenn die beiden orthogonalen inneren Zustände $\chi _{1}$ bzw. $\chi _{2}$ der Teilwellen rechtzeitig vor der irreversiblen quantenmechanischen Ortsmessung in denselben Zustand $\chi _{3}$ übergeführt werden. Dieser Übergang löscht die Welcher-Weg-Markierung, die Wellenfunktion ist dann $\Psi ({\vec {r}},s)=\left(\Phi _{1}({\vec {r}})+\Phi _{2}({\vec {r}})\right)\chi _{3}(s)$ und zeigt dasselbe Interferenzbild wie oben. Die Löschung muss zwischen dem Doppelspalt und dem Ort des Messprozesses stattfinden, also irgendwann nach Aufprägen der Welcher-Weg-Markierung, aber noch vor dem Auftreffen des Quantenobjekts auf dem Schirm.

Dieser Löschprozess kann ein verhältnismäßig einfacher Vorgang sein, wenn es sich wie oben bei dem einfachen Quantenradierer um Photonen und beim inneren Zustand um deren Polarisation handelt. Wenn $\chi _{-},\ \chi _{|}$ die beiden linear polarisierten Zustände mit synchron schwingendem elektrischen Feld bezeichnen, die durch die beiden gekreuzten Polarisationsfilter der Welcher-Weg-Markierung definiert sind, und wir als Beispiel ein einfallendes Photon in einem diagonal polarisierten Zustand $\chi _{\diagup }$ betrachten, dann zerlegt man dieses in die durch die beiden Polarisatoren definierten Basiszustände:

\chi _{\diagup }={\tfrac {1}{\sqrt {2}}}\left(\chi _{-}+\chi _{|}\right)

Die erste Komponente kommt ungeändert durch einen Polarisator, die zweite durch den anderen, und die jeweils unpassende Komponente wird absorbiert oder umgelenkt. Also ist $\chi _{1}=\chi _{-}$ und $\chi _{2}=\chi _{|}$ . Nun lässt der dritte, um 45° verdrehte Filter – der Quantenradierer – nur (beispielsweise) die linear polarisierten Photonen $\chi _{\diagdown }$ durch und blockiert die dazu senkrecht polarisierten $\chi _{\diagup }$ . Um die Wirkung auf die markierten Photonen $\chi _{-}$ bzw. $\chi _{|}$ zu ermitteln, zerlegt man diese gemäß der Basis $\chi _{\diagup }\;,\chi _{\diagdown }$ :

\chi _{-,|}={\tfrac {1}{\sqrt {2}}}\left(\chi _{\diagup }\pm \chi _{\diagdown }\right)

.

Wegen des unterschiedlichen Vorzeichens in dieser Formel sind die Zustände orthogonal, die Photonen also nicht interferenzfähig. Der Quantenradierer löscht nun in beiden die Komponente $\chi _{\diagup }$ , und es bleibt für beide nur derselbe Polarisationszustand $\chi _{\diagdown }$ . Damit sind sie wieder interferenzfähig. Allerdings haben sie in diesem Beispiel entgegengesetztes Vorzeichen, was für den Anteil des ursprünglichen Photons, der weiter zum Schirm fliegt, die Gesamtwellenfunktion

\Psi ={\tfrac {1}{2}}\left(\Phi _{1}-\Phi _{2}\right)\chi _{\diagdown }

.

ergibt. In ihrem neu entstandenen Interferenzmuster sind also gegenüber dem ursprünglichen die hellen und dunklen Streifen vertauscht. Genau das ursprüngliche Muster wird wieder hergestellt, wenn das einfallende Photon schon in demselben Polarisationszustand ist, der durch den letzten Polarisationsfilter hindurchkommt. Da man den insgesamt unpolarisierten Strom der einfallenden Photonen immer als Mischung aus Photonen auffassen kann, die je zur Hälfte in zwei zueinander senkrechten Richtungen polarisiert sind, geben die beiden einfachen Beispiele schon die allgemeine Beschreibung.

Handelt es sich um Interferenz von Atomstrahlen, ist die Löschung der Markierung viel schwieriger und bisher auch nicht im Experiment demonstriert worden. Zwar lässt sich das angeregte Atom vom Zustand $\chi _{2}$ wieder in den durch $\chi \ (=\chi _{1})$ charakterisierten Ausgangszustand bringen, es hat aber dann nicht unbedingt wieder dieselbe Wellenfunktion, sondern im Allgemeinen zusätzlich einen Phasenfaktor $\mathrm {e} ^{\mathrm {i} \alpha }$ , der auch noch bei jedem weiteren Atom unkontrolliert variieren würde. Nach Ausklammern der inneren Wellenfunktion $\chi \ (=\chi _{1})$ überlagern sich die Teilwellen dann zu

\Psi ({\vec {r}},s)=\left(\Phi _{1}({\vec {r}})+\mathrm {e} ^{\mathrm {i} \alpha }\Phi _{2}({\vec {r}})\right)\chi (s)

.

Der Ortsanteil darin erzeugt daher wieder ein Interferenzmuster, das aber gegenüber dem ursprünglichen in Abhängigkeit von der Phase $\alpha$ verwaschen und verschoben ist. Nur bei $\alpha =0$ oder $\pi$ zeigt sich das ursprüngliche bzw. das komplementäre Interferenzbild mit Vertauschung der hellen und dunklen Streifen. Bei statistisch fluktuierenden Phasen würden die verschiedenen Muster sich zu dem Bild der inkohärenten Überlagerung, also einem verwaschenen Streifen, ausmitteln.[7]

Delayed-Choice-Experiment

Der Quantenradierer zeigt besonders deutlich, dass bei einem Wechselwirkungsprozess eines Quantenobjekts mit der Art der Beobachtung ausgewählt werden kann, ob sich das Objekt wie eine Welle oder wie ein Teilchen verhält. „Delayed Choice“ (meist mit dem englischen Ausdruck angesprochen, manchmal eingedeutscht als „Verzögerte Quantenwahl“[21]) bedeutet hier, dass die Auswahl der Art der Beobachtung erst entschieden und in die Tat umgesetzt wird, nachdem die Wechselwirkung schon längst abgeschlossen ist. Die Objekte können auch schon den ganzen Apparat durchlaufen und im Extremfall sogar schon eine endgültige quantenmechanische Messung ausgelöst haben, bevor entschieden wird, ob die Beobachtung den Wellen- oder den Teilchencharakter zeigen soll. Dass die Quantenmechanik die Möglichkeit solcher paradox erscheinenden Phänomene voraussagt, wurde schon in den 1930er Jahren von Carl Friedrich von Weizsäcker entdeckt, aber erst in den 1980ern durch Archibald Wheeler in Fachkreisen populär gemacht. (Siehe den umfassenden Überblick[12].)

Dem Alltagsverstand mag sich die Annahme aufdrängen, die später gewählte Art der Beobachtung habe das frühere Verhalten des Quantenobjekts beeinflusst. Doch kann eine solche Umkehrung des Zeitablaufs von Ursache und Wirkung hiermit nicht belegt werden, denn der begriffliche Rahmen ist der falsche. Ganz grundsätzlich ist 2012 mithilfe der Bellschen Ungleichung gezeigt worden, dass eine Beschreibung des Quantenradierers im Rahmen der klassischen Physik (bzw. des Alltagsverstands), wo jedes Objekt zu jeder Zeit einen wohldefinierten Zustand einnimmt, nicht möglich ist.[22][23] Im vorliegenden Fall endet die (quantenmechanisch zu beschreibende) Wechselwirkung des Objekts mit der Apparatur nicht mit dem Durchgang durch den Doppelspalt, sondern mit einer irreversiblen Wechselwirkung im Detektor.

Damit bleibt noch zu erklären, wie dieses Phänomen im Experiment mit einzelnen Paaren verschränkter s- und i-Photonen auch dann noch hervorgerufen werden kann, wenn das s-Photon schon endgültig nachgewiesen wurde (und damit vernichtet ist), und eine spätere Messung des i-Photons scheinbar noch darüber entscheiden kann, ob das s-Photon sich als Welle oder als Teilchen verhalten hat. Richtig bleibt, dass die zeitlich frühere quantenmechanische Messung, die des s-Photons, eine Zustandsreduktion auslöst, die den verschränkten Zustand beider Photonen

\Psi _{s,i}=H_{s}\;V_{i}+V_{s}\;H_{i}\equiv \Phi _{s+}\,\Phi _{i-}-\Phi _{s-}\;\Phi _{i+}

auflöst[15]. Das i-Photon bleibt dann meistens in einem inkohärenten Zustandsgemisch von zwei Basispolarisationen übrig. Darunter kann man sich zum Zweck der einfachen Beschreibung die geeignete Basis beliebig auswählen, bis hierher sind sie alle gleichwertig.

Zur Verdeutlichung ein einfacher Fall: Ein s-Photon traf den Schirm an einer Stelle, die im Fall der sichtbaren Interferenzstreifen dunkel geblieben war. Dann kann dieses Messergebnis offenbar nicht von der Komponente mit $\Phi _{s+}$ in dem verschränkten Zustand herrühren, denn diese ist für das Interferenzmuster verantwortlich und hat dementsprechend im dunklen Interferenzstreifen die Auftreffwahrscheinlichkeit null. Damit ist dieses s-Photon auf den Zustand $\Phi _{s-}$ festgelegt, und damit das i-Photon in diesem Fall nicht auf ein Zustandsgemisch, sondern auf den reinen Zustand $\Phi _{i+}$ . Wenn dieser Zustand aber im Polarisator vor dem i-Detektor blockiert wird, weil nur der Anteil $\Phi _{i-}$ des i-Photons zur Zählung durchgelassen wird, dann kann kein s-Photon, das mit einem der so ausgewählten $\Phi _{i-}$ -Photonen koinzident ist, an diese Stelle gekommen sein. So wird die Intensitätsverteilung der s-Photonen, die die Koinzidenzbedingung erfüllen, eine andere sein als ohne diese Bedingung. Also ergibt sich an der betrachteten Stelle wirklich ein Minimum.

Hier handelt es sich ersichtlich nicht um eine zeitlich rückwirkende Beeinflussung des Verhaltens des s-Photons, auch nicht um die Wiederherstellung einer verlorengegangen Information, sondern um die zu einem beliebigen Zeitpunkt mögliche Auswahl derjenigen s-Photonen, die die bestimmte Eigenschaft hatten, dass das zugehörige i-Photon die richtige Polarisation besitzt. So erfüllt die in der Apparatur realisierte Koinzidenzbedingung zwar den Zweck, die Gleichzeitigkeit zweier Signale von s- und i-Photon festzustellen, dies aber nur, um sicherzustellen, dass das betreffende Photonenpaar wirklich von ein und demselben auf den Doppelspalt auffallenden Photon abstammt. Dennoch tauchen in populären Darstellungen hin und wieder Schlussfolgerungen hinsichtlich einer möglichen Rückwärtsverursachung auf, die auch in der wissenschaftlichen Literatur diskutiert werden (siehe z. B.[2][3]).

Komplementarität, Welle-Teilchen-Dualismus, Unschärfe-Relation, und „Welcher-Weg“-Information

In dem von Niels Bohr schon kurz nach Beginn der Entwicklung der Quantenmechanik entdeckten Komplementaritätsprinzip werden die Erfahrungen dahingehend zusammengefasst, dass die Quantenobjekte die charakteristischen Eigenschaften von Welle und Teilchen nie gleichzeitig zeigen können, weil diese sich gegenseitig ausschließen. Die für das Doppelspaltexperiment relevanten Eigenschaften sind bei einer Welle der gleichzeitige Durchgang durch beide Spalte, bei einem Teilchen die im Prinzip mögliche Kenntnis, durch welchen der Spalte sein Weg führte. Tatsächlich lassen sich die oben im Einzelnen dargestellten Abläufe ausnahmslos darin zusammenfassen, dass die Möglichkeit der Kenntnis des Teilchenweges ausreicht, um die Interferenz der Wellen auszuschließen. (Anzumerken ist, dass mit dem Verschwinden der Doppelspaltinterferenz nicht bewiesen ist, dass das betrachtete Quantenobjekt wirklich ein Teilchen ist. Denn das beobachtete Ausbleiben der Interferenz lässt sich auch dadurch erklären, dass die Wellen aus den beiden Spalten nur ihre gegenseitige Interferenzfähigkeit verloren haben. Dass es trotzdem Wellen geblieben sind, wird z. B. schon daran deutlich, dass die vom Durchgang durch einen einzigen Spalt verursachten Interferenzen am Rand des hellen zentralen Streifens immer noch nachzuweisen sind.)

Zur näheren Deutung der Komplementarität von Welle- und Teilchenbild wird oft auf die Unschärferelation von Werner Heisenberg verwiesen. Sie drückt aus, dass Ort und Impuls eines Quantenobjekts nicht gleichzeitig genau bekannt sein können, ja noch nicht einmal gleichzeitig genau definierte Größen sind. Steht der Wert von einer dieser Größen mit mathematischer Genauigkeit fest, ist der Wert der anderen vollkommen unbestimmt (und nicht etwa nur unbekannt). Der beste nach der Unschärferelation denkbare Kompromiss ist, dass beide Größen im Rahmen gewisser Unschärfebereiche liegen, deren Ausdehnungen zueinander umgekehrt proportional sind. Für die Verhältnisse am Doppelspalt ist eine Welcher-Weg-Markierung nur möglich, wenn die Unschärfe in der Kenntnis der Position kleiner als der Spaltabstand ist. Dann ist die Impulsunschärfe quer zu den Spalten, die gleichbedeutend ist mit der Unbestimmtheit der Ausbreitungsrichtung der Wellen, aber so groß, dass die Interferenzstreifen verwischt werden. In Heisenbergs originalem Gedankenexperiment hierzu entsteht die Impulsunschärfe durch einen Stoß mit einem Lichtquant genügend kurzer Wellenlänge, das in ein Mikroskop abgelenkt wird und so die Beobachtung ermöglicht, durch welchen Spalt das Teilchen fliegt. Damit ergibt sich aus der Unschärferelation eine physikalische Begründung der Komplementarität von Interferenz und Welcher-Weg-Information. Das oben erwähnte Gedankenexperiment mit Atomen und Mikrowellenresonatoren[7] hingegen würde – wenn es so durchführbar ist – diese Unschärfe unterbieten und trotzdem die Komplementarität von Wellen- und Teilchenverhalten zeigen. Demnach wäre die Komplementarität eine Eigenschaft der Quantenobjekte, die noch grundlegender wäre als die Unschärferelation. Die Voraussetzung ist, dass das Atom durch diese Markierung seines Weges keinen Stoß bekommt, der seinen Impuls unkontrollierbar verändert. Diese Voraussetzung wurde angezweifelt.[18][19][20]

Quellen

Michael Springer: Welle oder Teilchen - ein Test mit dem Quantenradierer. In: Spektrum der Wissenschaft. Band 1/1996. Spektrum der Wissenschaft Akademischer Verlag, 1996.
Anil Ananthaswamy: Quantenmechanik - kein Ausweg aus der Unwirklichkeit. In: Spektrum der Wissenschaft. Nr. 12, 2018, S. 13–19.

Weblinks

Quantenradierer mit einzelnen Photonen im Interferometer (Experiment interaktiv verfügbar)
Bauanleitung eines Quantenradiers (Quantenphysik in der Schule, im Webarchiv)
Ausführliche Beschreibung sowie Bau- und Experimentieranleitung zum Quantenradierer (Schülerlabor Physik (PSI), Karlsruher Institut für Technologie (KIT))
Download des Programms Programm „Quantum Eraser“, mit dem sich die Interferenz einzelner Photonen in einem Mach-Zehnder-Interferometer betrachten lässt (LMU München).

Einzelnachweise

Anil Ananthaswamy: Through two doors at once - the elegant experiment that captures the enigma of our quantum reality. Dutton, New York 2018, ISBN 978-1-101-98609-7. Eine gut lesbare Geschichte des Doppelspaltversuchs von Young bis zum Quantenradierer (englisch)
Alexander Wendt: Quantum Mind and Social Science: Unifying Physical and Social Ontolog. Cambridge University Press, Cambridge 2015, ISBN 1-316-29991-0, S. 202 ff.
G GalliCarminati, Flavie Martin: Quantum mechanics and the psyche. In: Physics of Particles and Nuclei. Band 39, Nr. 4, 2008, S. 560- 577, doi:10.1134/S1063779608040047.
Eintrag „Backward Causation“ in der Stanford Encyclopedia of Philosophy. Siehe auch die ausführliche Darstellung und Diskussion solcher Vorschläge in der englischen Wikipedia (abgerufen 2019-02-26)
Stuart Hameroff: How quantum brain biology can rescue conscious free will. In: Frontiers in integrative neuroscience. Band 6, 2012, S. 93 (online [abgerufen am 12. Februar 2019]).
Marlan O. Scully, Kai Drühl: Quantum eraser: A proposed photon correlation experiment concerning observation and "delayed choice" in quantum mechanics. In: Physical Review A. Band 25, Nr. 4, 1982, S. 2208–2213.
Marian O. Scully, Berthold-Georg Englert, Herbert Walther: Quantum optical tests of complementarity. In: Nature. Band 351, 9. Mai 1991, S. 111–116, doi:10.1038/351111a0.
Gymnasialer Lehrplan Baden-Württemberg (PDF; 43 kB)
Physik - Gymnasiale Oberstufe. Duden Paetec, 2005, ISBN 3-89818-311-4.
E Weisz, HK Choi, I Sivan, M Heiblum, Y Gefen, D Mahalu, V Umansky: An electronic quantum eraser. In: Science. Band 344, Nr. 6190, 2014, S. 2014-1366, doi:10.1126/science.1248459.
S. Dürr, T. Nonn, G. Rempe: Origin of quantum-mechanical complementarity probed by a ‘which-way’experiment in an atom interferometer. In: Nature. Band 395, 1998, S. 33–37 (online [PDF; abgerufen am 11. Februar 2019]). Hier wurde kein materieller Doppelspalt benutzt, sondern ein Gitter aus stehenden Lichtwellen. Die Anregungsenergie für die Welcher-Weg-Markierung betrug nicht mehr als einige µeV.
Xiao-song Ma, Johannes Kofler, and Anton Zeilinger: Delayed-choice gedanken experiments and their realizations. In: Rev. Mod. Phys. Band 88, 2016, S. 015005, doi:10.1103/RevModPhys.88.015005.
David Ellerman: Why delayed choice experiments do Not imply retrocausality. In: Quantum Studies: Mathematics and Foundations. Band 2, 2015, S. 183–199, doi:10.1007/s40509-014-0026-2.
S. P. Walborn, M. O. Terra Cunha, S. Pádua, C. H. Monken, Double Slit Quantum Eraser, Phys. Rev. A 65, 2002, S. 033818, doi:10.1103/PhysRevA.65.033818
Normierungsfaktoren werden für bessere Lesbarkeit hier weggelassen.
Yoon-Ho Kim, Rong Yu, Sergei P Kulik, Yanhua Shih, Marlan O Scully: Delayed "choice" quantum eraser. In: Physical Review Letters. Band 84, Nr. 1, 2000, S. 1.
Herbert Walther, B.-G. Englert, Marlan Scully: Komplementarität und Welle Teilchen Dualismus. In: Spektrum der Wissenschaft. Band 2. Spektrum der Wissenschaft Akademischer Verlag, 1995, S. 50 ff.
P. Storey, S. Tan, M. Collett, D. Walls: Path detection and the uncertainty principle, Nature. Band 367, S. 626–628, 17. Februar 1994.
Berthold-Georg Englert, Marian O. Scully, Herbert Walther: Complementarity and uncertainty. In: Nature. Band 375, 1995, S. 367–368, doi:10.1038/375367b0.
E. Pippa Storey, Sze M. Tan, Matthew J. Collett, Daniel F. Walls: Complementarity and uncertainty. In: Nature. Band 375, 1995, S. 368, doi:10.1038/375368a0.
Delayed-Choice-Experiment. In: Lexikon der Physik. Spektrum der Wissenschaft Verlagsgesellschaft, 1998, abgerufen am 21. Februar 2019.
A. Peruzzo, P. Schadbolt, N. Brunner, S. Popescu, J. O'Brien: A quantum delayed choice experiment. In: Science. Band 338, 2012, S. 634–637, doi:10.1126/science.1226719.
F. Kaiser, Th. Coudeau, P. Milman, B. Ostrowsky, S. Tanzilli: Entanglement-Enabled Delayed-Choice Experiment. In: Science. Band 338, 2012, S. 637–640, doi:10.1126/science.1226755.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Anil Ananthaswamy: Through two doors at once - the elegant experiment that captures the enigma of our quantum reality. Dutton, New York 2018, ISBN 978-1-101-98609-7. Eine gut lesbare Geschichte des Doppelspaltversuchs von Young bis zum Quantenradierer (englisch)

[Wendt2015-2] Alexander Wendt: Quantum Mind and Social Science: Unifying Physical and Social Ontolog. Cambridge University Press, Cambridge 2015, ISBN 1-316-29991-0, S. 202 ff.

[CarminatiFlavie2008-3] G GalliCarminati, Flavie Martin: Quantum mechanics and the psyche. In: Physics of Particles and Nuclei. Band 39, Nr. 4, 2008, S. 560- 577, doi:10.1134/S1063779608040047.

[4] Eintrag „Backward Causation“ in der Stanford Encyclopedia of Philosophy. Siehe auch die ausführliche Darstellung und Diskussion solcher Vorschläge in der englischen Wikipedia (abgerufen 2019-02-26)

[Hameroff2012-5] Stuart Hameroff: How quantum brain biology can rescue conscious free will. In: Frontiers in integrative neuroscience. Band 6, 2012, S. 93 (online [abgerufen am 12. Februar 2019]).

[6] Marlan O. Scully, Kai Drühl: Quantum eraser: A proposed photon correlation experiment concerning observation and "delayed choice" in quantum mechanics. In: Physical Review A. Band 25, Nr. 4, 1982, S. 2208–2213.

[ScullyEnglertWalther1991-7] Marian O. Scully, Berthold-Georg Englert, Herbert Walther: Quantum optical tests of complementarity. In: Nature. Band 351, 9. Mai 1991, S. 111–116, doi:10.1038/351111a0.

[GymBW-8] Gymnasialer Lehrplan Baden-Württemberg (PDF; 43 kB)

[GymDuden-9] Physik - Gymnasiale Oberstufe. Duden Paetec, 2005, ISBN 3-89818-311-4.

[Weisz2014-10] E Weisz, HK Choi, I Sivan, M Heiblum, Y Gefen, D Mahalu, V Umansky: An electronic quantum eraser. In: Science. Band 344, Nr. 6190, 2014, S. 2014-1366, doi:10.1126/science.1248459.

[Dürr1998-11] S. Dürr, T. Nonn, G. Rempe: Origin of quantum-mechanical complementarity probed by a ‘which-way’experiment in an atom interferometer. In: Nature. Band 395, 1998, S. 33–37 (online [PDF; abgerufen am 11. Februar 2019]). Hier wurde kein materieller Doppelspalt benutzt, sondern ein Gitter aus stehenden Lichtwellen. Die Anregungsenergie für die Welcher-Weg-Markierung betrug nicht mehr als einige µeV.

[MaKofZeilinger_2016-12] Xiao-song Ma, Johannes Kofler, and Anton Zeilinger: Delayed-choice gedanken experiments and their realizations. In: Rev. Mod. Phys. Band 88, 2016, S. 015005, doi:10.1103/RevModPhys.88.015005.

[13] David Ellerman: Why delayed choice experiments do Not imply retrocausality. In: Quantum Studies: Mathematics and Foundations. Band 2, 2015, S. 183–199, doi:10.1007/s40509-014-0026-2.

[14] S. P. Walborn, M. O. Terra Cunha, S. Pádua, C. H. Monken, Double Slit Quantum Eraser, Phys. Rev. A 65, 2002, S. 033818, doi:10.1103/PhysRevA.65.033818

[unnormiert-15] Normierungsfaktoren werden für bessere Lesbarkeit hier weggelassen.

[Kim1999-16] Yoon-Ho Kim, Rong Yu, Sergei P Kulik, Yanhua Shih, Marlan O Scully: Delayed "choice" quantum eraser. In: Physical Review Letters. Band 84, Nr. 1, 2000, S. 1.

[17] Herbert Walther, B.-G. Englert, Marlan Scully: Komplementarität und Welle Teilchen Dualismus. In: Spektrum der Wissenschaft. Band 2. Spektrum der Wissenschaft Akademischer Verlag, 1995, S. 50 ff.

[PippaStorey-18] P. Storey, S. Tan, M. Collett, D. Walls: Path detection and the uncertainty principle, Nature. Band 367, S. 626–628, 17. Februar 1994.

[EnglertReplik1-19] Berthold-Georg Englert, Marian O. Scully, Herbert Walther: Complementarity and uncertainty. In: Nature. Band 375, 1995, S. 367–368, doi:10.1038/375367b0.

[StoreyReplik2-20] E. Pippa Storey, Sze M. Tan, Matthew J. Collett, Daniel F. Walls: Complementarity and uncertainty. In: Nature. Band 375, 1995, S. 368, doi:10.1038/375368a0.

[21] Delayed-Choice-Experiment. In: Lexikon der Physik. Spektrum der Wissenschaft Verlagsgesellschaft, 1998, abgerufen am 21. Februar 2019.

[22] A. Peruzzo, P. Schadbolt, N. Brunner, S. Popescu, J. O'Brien: A quantum delayed choice experiment. In: Science. Band 338, 2012, S. 634–637, doi:10.1126/science.1226719.

[23] F. Kaiser, Th. Coudeau, P. Milman, B. Ostrowsky, S. Tanzilli: Entanglement-Enabled Delayed-Choice Experiment. In: Science. Band 338, 2012, S. 637–640, doi:10.1126/science.1226755.