Quanten-Zeno-Effekt
Der Quanten-Zeno-Effekt ist ein Effekt aus der Quantenmechanik, bei dem der Übergang eines quantenmechanischen Systems von einem Zustand in einen anderen, z. B. durch Lichtaussendung eines angeregten Atoms, durch wiederholt ausgeführte Messungen aufgehalten werden kann. Damit erinnert der Effekt an das Pfeil-Paradoxon des griechischen Philosophen Zenon von Elea. Der Begriff stammt von George Sudarshan und B. Misra.[1]
Bildhafte Argumentation
Wenn ein Atom spontan zerfällt, so geschieht dies nach den Gesetzen der Quantenmechanik nicht zu einem vorbestimmten Zeitpunkt, sondern zufällig, d. h. nach rein statistischen Gesetzmäßigkeiten. Dieses Ereignis kann am einfachsten als Superposition (Überlagerung) der Zustände A (nicht zerfallen) und B (zerfallen) aufgefasst werden. Von diesem Überlagerungszustand aus gibt es dann eine gewisse Wahrscheinlichkeit, mit der sich der Zerfall ereignet. Bei einem spontan zerfallenden System steigt diese Wahrscheinlichkeit mit dem Fortschreiten der Zeit. Wenn nun zu einem gewissen Zeitpunkt nachgesehen wird, ob das Atom bereits zerfallen ist oder nicht, so findet man entweder Zustand A (Atom nicht zerfallen) oder B (Atom zerfallen) vor. Dies entspricht einer quantenmechanischen Messung mit der grundlegenden Eigenschaft, dass nur Eigenzustände des Messoperators (also A oder B) und keine Überlagerungszustände detektiert werden können. Die Wahrscheinlichkeit für das Vorfinden von Zustand A bzw. B ist durch den Gewichtsanteil des jeweilig gemessenen Zustands in der Überlagerung gegeben, der sich mit der Zeit immer mehr von A nach B verschiebt. Durch den Messprozess selbst wird die Wellenfunktion zu Zustand A oder B reduziert, wobei man dann von einem Kollaps der Wellenfunktion spricht.
Wenn nun am Anfang das einzelne Atom im Zustand A (nicht zerfallen) ist, dann ist der Anteil des Zustandes B (zerfallen) nach kurzer Zeit äußerst gering. Bei einer Messung wird es also mit sehr hoher Wahrscheinlichkeit noch nicht zerfallen sein. Durch die Beobachtung geht es in diesem Fall wieder in den Eigenzustand A (zu 100 % nicht zerfallen) über, und der Zerfallsvorgang beginnt wieder von Neuem.
Insgesamt bekommt man somit bei häufiger Beobachtung eine Zerfallsrate, die deutlich unter der unbeobachteten Zerfallsrate liegt. Lässt man die Abstände der Beobachtungen gegen null gehen, was einer Dauerbeobachtung gleichkommt, so geht auch die Zerfallswahrscheinlichkeit gegen null, d. h. das dauernd beobachtete Atom sollte aufgrund dieser Beobachtung gar nicht mehr zerfallen.
Der Quanten-Zeno-Effekt wurde von mehreren Gruppen weltweit mithilfe von Methoden der Lasertechnik und Atomphysik experimentell bestätigt.[2][3][4][5][6]
Eine deutschsprachige populärwissenschaftliche Aufarbeitung erschien 1994 nach Messungen an der Ludwig-Maximilians-Universität München: Die Bewegung eines Quantensystems wurde dort nachweislich alleine durch eine Folge dichter Messungen zum Stillstand gebracht, was die theoretische Modellierung des Quanten-Zeno-Effekts untermauerte.[7]
Allgemeine Voraussetzung
Vorbedingungen aus der Quantentheorie für das Zustandekommen des Effektes:
- Der Messoperator und der Zeitentwicklungsoperator vertauschen nicht miteinander.
- Zwischen den Messungen entwickelt sich das System kohärent (ungestört).
Analogie: Ein umgekehrter Zeno-Effekt in der Optik
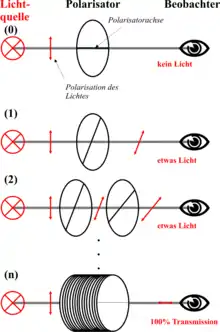
Ein auch im Rahmen der klassischen Physik beschreibbares Experiment, das dazu dient, sich einem Verständnis des Zeno-Effektes zu nähern, besteht aus einer polarisierten Lichtquelle und mehreren Polarisatoren, wie in nebenstehender Abbildung gezeigt.
Zunächst (Abb. (0)) ist das Licht aus der Lichtquelle rein vertikal polarisiert. Bei freier Ausbreitung ändert sich diese Ausrichtung nicht, wird also nie horizontal polarisiert sein. Ein horizontaler Polarisator führt daher immer zur Auslöschung.
Fügt man nun einen gegen die Polarisationsrichtung des Lichtes um verdrehten Polarisator hinzu, so sinkt die Intensität beim Beobachter proportional zu , da nur die Projektion der Schwingungsebene auf die Polarisatorachse durchgelassen wird. Interessant ist aber vor allem, dass dieser Polarisator eine quantenmechanische Messung darstellt. Danach liegt also die Polarisationsebene parallel zur Polarisatorachse (Abb (1)), was einer quantenmechanischen Zustandspräparation entspricht.
Fügt man nun Polarisatoren hintereinander, im Grenzfall: , die jeweils zueinander nur um einen infinitesimalen Winkel verdreht sind, so ist der Verlust pro Polarisator minimal und geht im Grenzfall gegen null. Somit kann man rein durch hintereinander ausgeführte verlustfreie Messungen die Polarisationsrichtung drehen, d. h. die Erwartungsgröße der Observablen ändern. Dieses Szenario entspricht in etwa der oben beschriebenen kontinuierlichen Messung.
Kritik und andere Aspekte
Bisher wurde noch kein Anhalten des radioaktiven Zerfalls durch experimentelle Messungen eines Ensembles von radioaktiven Atomen oder gar eines einzelnen radioaktiven Atoms bestätigt, wie es die Theorie des Quanten-Zeno-Effekts erfordern würde. Vor allem stellt das Gegenteil, die Umkehrung des Zeno-Effekts, keine Analogie, sondern nur einen konträren oder polaren Gegensatz dar. Die Experimente von Itano und Mitarbeitern[2] beziehen sich auf stabile Isotope von 9Be in Mischungen mit 26Mg, wobei Übergänge im UV-Bereich stimuliert und beobachtet wurden. Da das quantenmechanische System in diesem Fall a priori durch den Beobachter definiert oder gestört wurde, kann grundsätzlich nicht von der Beobachtung eines indeterminierten Systems ausgegangen werden, wodurch der experimentelle Ansatz in Frage gestellt wird. Tatsächlich ist es wahrscheinlicher, dass der entsprechende quantenmechanische Prozess, insbesondere der radioaktive Zerfall, sogar beschleunigt wird, wenn er mit hoher Beobachtungsfrequenz untersucht wird.[8]
Literatur und Weblinks
- Christian Speicher: "Trügerische Bewegung in der Quantenwelt. Eine moderne Version von Zenos Paradoxon. Messung als Eingriff mit weitreichenden Folgen." – Natur und Wissenschaft (Beilage der Frankfurter Allgemeinen Zeitung), 6. April 1994, N1 f.
- PDF, Quantenmechanische Paradoxa (1,01 MB)
- NZZ Forschung und Technik, populärwiss. Artikel über den QM-Zeno-Effekt (Memento vom 27. Mai 2008 im Internet Archive)
- http://www.spektrum.de/magazin/zeno-und-der-quanten-schnellkochtopf/828346
Quellen
- B. Misra and E.C.G. Sudarshan: The Zeno's paradox in quantum theory. J. Math. Phys. 18, 756-763 (1977)
- W. M. Itano, D. J. Heinzen, J. J. Bollinger, D. J. Wineland: Quantum Zeno effect. Phys. Rev. A 41, 2295-2300 (1990)
- M. C. Fischer, B. Gutiérrez-Medina M. G. Raizen: Observation of the Quantum Zeno and Anti-Zeno effects in an Unstable System. Physical Review Letters 87, 040402 (2001)
- Chr. Wunderlich, Chr. Balzer, and P. E. Toschek: Evolution of an Atom Impeded by Measurement: The Quantum Zeno Effect. In: Zeitschrift für Naturforschung A. 56, 2001, S. 160–164 (PDF, freier Volltext).
- Chr. Balzer, R. Huesmann, W. Neuhauser, P.E. Toschek, The Quantum Zeno Effect - Evolution of an Atom Impeded by Measurement. Opt. Comm. 180 (2000) 115-120, quant-ph/0105004
- Chr. Balzer, Th. Hannemann, D. Reiß, Chr. Wunderlich, W. Neuhauser, P.E.Toschek: A relaxationless demonstration of the Quantum Zeno Paradox on an individual atom. Optics Communications Vol. 211, 235-241 (2002), quant-ph/0406027
- Christian Speicher: "Trügerische Bewegung in der Quantenwelt. Eine moderne Version von Zenos Paradoxon. Messung als Eingriff mit weitreichenden Folgen." - Natur und Wissenschaft (Beilage der Frankfurter Allgemeinen Zeitung), 6. April 1994, N1 f.
- Zeno's Quantum Paradox Reversed: Watching A Flying Arrow Increase Its Speed