Astronomische Refraktion
Astronomische Refraktion ist die Richtungsänderung eines von außen auf die Erde fallenden Lichtstrahls durch Brechung in der geschichteten Atmosphäre. Ursache ist der Anstieg des Brechungsindex von n=1 im Vakuum des Weltalls auf etwa n=1,00029 am Erdboden. Die astronomische Refraktion ist ein Spezialfall der terrestrischen Refraktion.
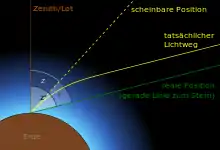

Die Krümmung der Lichtstrahlen erfolgt nach unten – im selben Sinn wie die Erdkrümmung, aber wesentlich weniger. Die stärkste Krümmung tritt in Bodennähe auf und macht bei sehr flachen Visuren maximal 10–15 % der Erdkrümmung aus.
Auf Meereshöhe und ausgedrückt im Winkelmaß beträgt die astronomische Refraktion je nach Temperatur
- etwa 0,6 Grad (34′ bis 39′) für horizontal einfallende Lichtstrahlen – also beim Auf- oder Untergang eines Gestirns,
- etwa 29′ bei einem halben Grad über dem Horizont,
- etwa 5′ bei einem Höhenwinkel von 10°,
- etwa 1′ (55″ bis 65″) in einem Höhenwinkel von 45°
- und Null bei senkrechtem Einfallswinkel – also im Zenit.
- Sie folgt einer komplizierten Formel mit mehreren atmosphärischen Parametern und Winkelfunktionen der Zenitdistanz (z = 90° minus Höhenwinkel). Für Zenitdistanzen z < 70° kann man für die Refraktion r auf Meeresniveau bei durchschnittlichem Luftdruck näherungsweise schreiben:
Sterne erscheinen angehoben
Die Erdatmosphäre ist nahe der Erdoberfläche dichter als in größeren Höhen. Deshalb werden vom Weltraum her schräg einfallende Lichtstrahlen durch die astronomische Refraktion zunehmend nach unten gebogen. Einem Beobachter auf der Erde erscheinen demnach Gestirne, wenn sie nicht ungefähr im Zenit stehen, höher, als es ohne die irdische Lufthülle der Fall wäre, Der Betrag der Refraktion hängt vom Tangens der Zenitdistanz sowie von Temperatur und Luftdruck am Ort des Beobachters ab. In 5 km Höhe wird etwa die Hälfte des Wertes auf Meeresniveau erreicht.
Ursache der astronomischen Refraktion ist die Brechung, die jeder Lichtstrahl beim Übertritt aus einem optisch dünneren in ein dichteres Medium erfährt. Die Änderung der Ausbreitungsrichtung tritt in differentiell kleinen Schritten zwischen benachbarten Luftschichten auf (Snelliussches Brechungsgesetz) und muss über den gesamten Lichtweg integriert werden.
Hierfür ist ein geeigneter Ansatz des Temperatur- und Druckverlaufs nach der Höhe notwendig – eine sogenannte Norm- oder Standardatmosphäre (bodennah: 15 °C Temperatur und 1013,25 hPa Luftdruck, vertikaler Temperaturgradient −6 bis 7 K/km). Genähert kann man sie berechnen, indem man die Atmosphäre als 8 km dicke planparallele Platte aus Luft ansetzt („Höhe der homogenen Atmosphäre“).
Tatsächlich weicht die astronomische Refraktion von diesem Standardwert ab, wenn die Luftschichten nicht regulär gelagert sind. Liegen sie geringfügig schräg – was über jedem Gebirgszug wegen der Sonnen- und Schattenseite der Fall ist – tritt im Zenit statt des Wertes 0 die sogenannte Zenitrefraktion auf.[1]
Solche Refraktionsanomalien können 0,2″[1] und mehr erreichen und sind der Grund, warum in der Astronomie und Geodäsie ausgeklügelte Messverfahren erforderlich sind, wenn eine Messgenauigkeit von besser als 1″ gewünscht wird. Sie sind auch ein wesentlicher Grund, warum sich durch Astrometriesatelliten wie Hipparcos die Genauigkeit der Astrometrie von 0,01″ bis 0,1″ auf 0,001″ steigern lässt.
Kleine Temperatur-Änderungen innerhalb des optischen Systems von Fernrohr, Kuppel der Sternwarte oder Kamera bzw. Sensor oder durch Abkühlung während der Nacht bewirken ebenfalls kleine Anomalien. Um sie unter der Messgenauigkeit zu halten, muss man die Instrumente vor Gebrauch an die Umgebungstemperatur angleichen bzw. die Saalrefraktion der Kuppel oder der Fernrohröffnung modellieren. Dies ist besser möglich, wenn die Einstrahlung verringert wird, etwa durch einen weißen Anstrich der Kuppel oder durch Temperaturregelung im Innern von Fernrohr oder Satellit.
Terrestrische und Satelliten-Refraktion
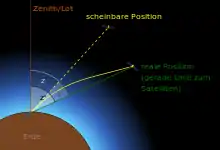
Verläuft ein Lichtstrahl zur Gänze innerhalb der Atmosphäre, so spricht man von „terrestrischer Refraktion“. Sie tritt bei jeder geodätischen Messung an der Erdoberfläche auf und wirkt der Erdkrümmung um etwa ein Siebentel entgegen. Dieser Faktor heißt Refraktionskoeffizient (übliches Formelzeichen k) und wurde bereits um 1800 von Carl Friedrich Gauß genau bestimmt. Bei der Hannover’schen Landesvermessung erhielt Gauß als Durchschnittswert 13 % der Erdkrümmung (k = 0,13).
Man kann die terrestrische Refraktion auf ähnliche Art modellieren bzw. berechnen wie die astronomische Refraktion, doch spielen lokale Temperaturänderungen der Luft eine größere Rolle. Nimmt die Lufttemperatur nach oben nicht wie bei der Normalatmosphäre mit 0,6 °C pro 100 Meter ab, krümmt sich ein Lichtstrahl stärker oder schwächer als normal. Bekannt ist der Spiegeleffekt über heißem Asphalt, wenn man – etwa auf der Autobahn – in flachem Winkel daraufblickt. Hier ist der Refraktionskoeffizient der bodennahen Luftschichten sogar negativ (Refraktionskoeffizient bis −2,0). Verlaufen die Messstrahlen in größerer Höhe über dem Gelände, kann k immer noch zwischen 0,10 und 0,15 variieren. Diese Anomalien (Abweichungen der Luftschichten von der Kugelform) begrenzen die Genauigkeit, mit der die Höhe von Vermessungspunkten bestimmt werden kann, auf einige Millimeter bis Zentimeter.
Bei der Messung zu Satelliten wiederum beginnt bzw. endet der Lichtstrahl nicht in völligem Vakuum, und das Ziel ist auch nicht „unendlich“ weit entfernt wie ein Gestirn. Dadurch tritt ein parallaktischer Effekt auf, der einige Prozent der astronomischen Refraktion ausmachen kann (kleiner Winkel s im obigen Bild), bei Satelliten in sehr tiefen Umlaufbahnen (englisch Low Earth Orbit, LEO) jedoch auch mehr.
Differentielle Refraktion
Astronomische Objekte bewegen sich bedingt durch die Erdrotation scheinbar auf Kreisbögen über den Himmel. Mit Ausnahme der Himmelspole ändert sich die Höhe bzw. der Zenitabstand eines Objektes dabei ständig. Da die astronomische Refraktion stark nicht-linear mit dem Zenitabstand zunimmt, wird sich ein Objekt nahe am Horizont für den Beobachter scheinbar etwas langsamer auf seinem (durch die Refraktion leicht verbogenen) Kreisbogen bewegen als ein Objekt mit kleinerem Zenitabstand.
Auf Langzeitbelichtungen des Sternhimmels kann das Bildfeld immer nur für einen Stern mittels eines sog. Leitsterns durch entsprechende Korrekturen des Fernrohr-Antriebs punktförmig abgebildet werden. Alle anderen Sterne werden durch die unterschiedlichen Zenitabstände, die sie während der Belichtung durchlaufen, zu Strichen auseinandergezogen. Dieser Effekt ist für die horizontnahen Sterne überproportional ausgeprägt und führt bei Weitwinkel-Aufnahmen zu tropfenförmigen Sternabbildungen in Horizontnähe. Dieser Effekt kann mit Bildbearbeitungsprogrammen nur ungenügend korrigiert werden.
Atmosphärische Dispersion
Als atmosphärische Dispersion wird die unterschiedlich starke Brechung von Licht verschiedener Wellenlängen bezeichnet. Blaues Licht wird stärker gebrochen als rotes, sodass der obere Rand beobachteter Himmelsobjekte blau gesäumt ist, der untere hingegen rot (siehe Korrektor (Teleskop)).
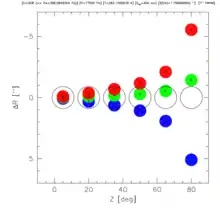
Sie macht sich bei Höhenwinkeln unter etwa 20° überdeutlich bemerkbar. Bereits bei 45° Höhe beträgt die Dispersion zwischen blauem und rotem Licht größer als 1" und begrenzt damit das Auflösungsvermögen von Teleskopen bereits ab ca. 100 mm Öffnung. Dieser Effekt lässt sich sehr deutlich an Venus, Merkur oder anderen hellen und tief stehenden Objekten schon bei relativ geringer Vergrößerung beobachten.
Solange man nur in einem schmalbandigen Spektralbereich beobachtet, spielt die Atmosphärische Dispersion nur eine untergeordnete Rolle. Sie lässt sich bei elektronischen Farbkameras mit einem RGB-Farbsensor ebenso wie bei Einzelaufnahmen mit RGB-Filtern teilweise korrigieren, indem mit einer geeigneten Software die 3 Farbauszüge für Rot, Grün und Blau entsprechend der atmosphärischen Dispersion leicht verschoben wieder zu einem Farbbild überlagert werden,
Bei professionellen Groß-Teleskopen wird schon seit längerem ein variabel einstellbarer Korrektor in den Strahlengang gebracht, mit dem die Auswirkungen der atmosphärischen Dispersion in Abhängigkeit von der Höhe korrigiert werden können und das Auflösungsvermögen des Teleskops auch bei Aufnahmen im gesamten zugänglichen Spektralbereich erhalten bleiben kann.
Für Amateurteleskope gibt es seit einiger Zeit ebenfalls mehr oder weniger komplexe Korrektoren, sog. „Atmosphärische Dispersions-Kompensatoren“ oder (englisch) „Atmospheric Dispersion Compensator“, abgekürzt ADC.[2]
Wirkung auf Entfernungsmessungen
Manchmal wird der Begriff Refraktion auch für die atmosphärischen Effekte in der Entfernungsmessung verwendet, wo nicht die Änderung des Winkels, sondern der Wellenlänge entscheidend ist. Auch hier sind für eine präzise Reduktion von Messwerten relativ komplizierte Formeln nötig, von denen jene des finnischen Geodäten Juhani Saastamoinen[3] (1972) für Änderung einer EDM-Messstrecke durch die Atmosphäre die bekannteste ist:
Darin ist die Zenitdistanz, die geografische Breite, die mittlere Höhe der Punkte, der mittlere Luftdruck, die integrale Lufttemperatur (in Kelvin) und der Dampfdruck sowie den weiteren Parametern und .
Zufällige Brechungseffekte in der Atmosphäre
Turbulenzen in der Erdatmosphäre vergrößern und verkleinern das Bild eines Sternes, so dass er mehrmals in der Sekunde heller und blasser erscheint. Dieses vom Auge wahrgenommene Blinken wird Szintillation genannt.
Zudem treten Bildunschärfe und Bildbewegungen auf. Alle drei Effekte werden unter dem Begriff Seeing zusammengefasst.
Dazu kommt noch der Einfluss der Saalrefraktion – eine geringfügige Lichtablenkung am Spalt der Sternwartekuppel, wenn zwischen Innen- und Außentemperatur noch ein kleiner Unterschied besteht.
Siehe auch
Literatur
- Karl Ramsayer: Geodätische Astronomie. Band IIa des Handbuchs der Vermessungskunde, J.B. Metzler-Verlag, Stuttgart 1969
- Refraktionstafeln in Lehr- oder Jahrbüchern der Astronomie oder Meteorologie
- Astro-geodätische Refraktionstafeln des Berliner Astronomischen Jahrbuches (bis 1960) oder in Internationale Astronomische Union (IAU)-Institutionen (ARI Heidelberg etc.)
- Christian Hirt: Monitoring and analysis of anomalous refraction using a digital zenith camera system.. In: Astronomy and Astrophysics. 459, Nr. 1, 2006, S. 283–290. doi:10.1051/0004-6361:20065485.
Weblinks
- Juergen Weiprecht: Kugelschalenmodell der Atmosphäre - allgemeine Theorie der Refraktion (Memento vom 18. Mai 2008 im Internet Archive) Astrophysikalisches Institut und Universitäts-Sternwarte, Friedrich-Schiller-Universität Jena
- Aufbau der Atmosphäre, Vergleich von Refraktionsmodellen
- Anomalie der Refraktion an untergehender Mondsichel
- Java-Applet als Rechenhilfe zur atmosphärischen Refraktion
Einzelnachweise
- Christian Hirt: Monitoring and analysis of anomalous refraction using a digital zenith camera system.. In: Astronomy and Astrophysics. 459, Nr. 1, 2006, S. 283–290. doi:10.1051/0004-6361:20065485.
- Peter Oden: Was ist eigentlich ... ein Atmospheric Dispersion Corrector (ADC)? In: Abenteuer Astronomie. 12. Juni 2017, abgerufen am 18. Oktober 2020 (deutsch).
- J. Saastamoinen: Contributions to the theory of atmospheric refraction. In: Bulletin Géodésique. Band 105, Nr. 1, 1972, S. 279–298, doi:10.1007/BF02521844.