Sichtbarkeit (Astronomie)
Als Sichtbarkeit eines astronomischen Objekts bezeichnet man die Zeit zwischen seinem scheinbaren Auftauchen über dem Horizont des eigenen Standortes (Aufgang), und dem Verschwinden des Gestirns unter dem örtlichen Horizont (Untergang).

Die Ursache der Erscheinung ist die Rotation der Erde bzw. eines anderen Standortes – etwa des Mondes – und (in geringerem Ausmaß) die Eigenbewegung des Objekts gegenüber dem Beobachter: In der Raumfahrt und für Erdsatelliten ist die Bahngeschwindigkeit des Flugkörpers der vorherrschende Einfluss.
Auf- und Untergänge sind neben der Kulmination die wichtigsten Aspekte der Astronomischen Phänomenologie, weshalb alle astronomischen Kalender bzw. Jahrbücher entsprechende Daten für Sonne und Mond enthalten. Die Berechnung erfolgt mit den sphärischen Formeln des Astronomischen Dreiecks.
Überblick
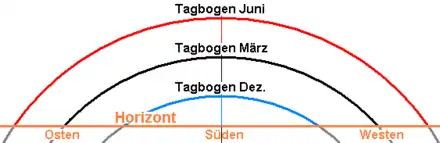
Die Zeit zwischen Auf- und Untergang eines Himmelskörpers wird in der Astronomie als Tagbogen bezeichnet. Bei völlig flachem Horizont teilt er sich in zwei gleiche Abschnitte: Vom Aufgang bis zum Höchststand (Kulmination oder Meridiandurchgang) im Süden – bzw. auf der Südhalbkugel im Norden – und von dort bis zum Untergang.
Dieser Zusammenhang gilt für einen topozentrischen Standort auf jedem Himmelskörper. Speziell auf der Erde gelten folgende Besonderheiten:
Bei Fixsternen verfrühen sich alle drei Zeitpunkte täglich um 4 Minuten, weil die Erde für eine Drehung nicht 24 Stunden, sondern nur 23,934 Stunden braucht (siderischer Tag). Bei der Sonne kommt noch der Einfluss der Jahreszeiten hinzu: Die Kulminationszeit (wahrer Mittag) kann um ±16 Minuten variieren (Zeitgleichung), die Auf- und Untergänge in Mitteleuropa sogar um ±2 Stunden (siehe Sonnenaufgang und Sonnenuntergang). Auf- und Untergangszeitpunkte des Mondes können – aufgrund der von der Sonnenposition unabhängigen Bahn des Mondes – zu jeder Tageszeit stattfinden.
Die Richtung bzw. der Zeitpunkt von Auf- und Untergängen hängt vor allem von drei Faktoren ab:
- Geografische Breite B des Standortes
- Deklination D des Gestirns (Winkelabstand von Himmelsäquator)
- Höhe des natürlichen Horizonts.
Mathematischer Auf-/Untergang
Die beiden erstgenannten Faktoren bestimmen den mathematischen Auf- und Untergang am idealen Horizont:
Diese an sich einfache Bedingung stellt sich in der Praxis der Ephemeridenrechnung äußerst komplex dar: In der Ableitung der Position in Bezug zum Beobachter aus der wahren Bahnkurve über die diversen astronomischen Koordinatensysteme ist die Ermittlung der Horizonthöhe der letzte Schritt, in den alle Irregularitäten der Himmelsmechanik, der Geodäsie, der Atmosphärischen Optik und auch der Relativitätstheorie – von Bahnstörungen der Bahn selbst über die Komplexitäten der Bewegung der Erde (Erdbahn, Erdrotation) als Beobachtungsort erster Näherung bis hin zur nicht-idealen Form des Geoids als wahrer Standpunkt des Beobachters und alle anderen Störungen auf der Sichtachse Objekt–Beobachter – einfließen. Daher gibt es keine geschlossenen Formeln für die Höhe, die sich nullsetzen ließen, sondern nur mehr oder minder präzise und/oder aufwändige Näherungen. Am einfachsten ist die Auf-/Untergangsrechnung für die „Fixsterne“ (die darum auch ihren Namen haben), neben irregulären Himmelskörpern wie Asteroiden und Kometen gilt die Berechnung für den Mond als die komplexeste (und diese Rechnung war auch eine der wichtigsten Triebfedern in der frühen Entwicklung der Mondtheorie) – die „Wandelgestirne“ haben davon ebenfalls ihren Namen; und die Auf-/Untergangsrechnung gilt als eine der aufwändigsten Problematiken der astronomischen Phänomenologie wie auch als leistungsfähiges Eichmaß der theoretischen Himmelsmechanik und numerischer Methoden der Ephemeridenrechnung.
Auf- und Untergang nichtzirkumpolarer Objekte
Zu einem (mathematischen) Auf- oder Untergang kommt es nur, wenn ein Gestirn (Sonne, Mond, Stern usw.) vom Himmelsäquator einen geringeren Winkelabstand hat als der Standort vom Nordpol (bzw. auf der Südhemisphäre vom Südpol).
- oder bzw.
- D ..Deklination, P ..Poldistanz, B ..Geografische Breite (positiv für die Nordhalbkugel)
Andernfalls steht das Gestirn immer über dem Horizont („Zirkumpolarstern“) oder bleibt immer unter dem Horizont, das heißt, es gibt gar keine Auf- und Untergänge (Sichtbarkeitsbedingung).
Sonnenaufgang und -untergang
Bei der Sonne verändert sich die Deklination im Zyklus der Jahreszeiten zwischen +23,4° und −23,4° (siehe Ekliptikschiefe). Daher kann sie jenseits der Polarkreise (B=+66,6° bzw. −66,6°) zeitweilig zirkumpolar sein (Polartag im Sommer) oder wochenlang unsichtbar (Polarnacht im Winter). Auf den Polen ist dies jeweils ein halbes Jahr der Fall (Mitternachtssonne), am Polarkreis (theoretisch) nur einen Tag.
Außerdem ist der Moment des Aufgangs bei der Sonne definiert als der Moment, in dem die Oberkante der Sonnenscheibe den Horizont überschreitet [2] (der Untergang entsprechend). Dieser findet etwas früher statt als der Aufgang des theoretischen Mittelpunkts der Sonnenscheibe und variiert mit der im Jahresablauf schwankenden Entfernung von Erde und Sonne (Apsidendistanz) und daraus folgend dem scheinbaren Durchmesser der Sonne, im Mittel beträgt er 0°32′.
Zusammen mit der weiter unten beschriebenen Lichtbrechung ergibt das insgesamt etwa 4 Minuten (−0°53′ in Höhe[1]), am Äquator verkürzt sich der Vorgang wegen der steileren Sonnenbahn auf 2,1 Minuten. Der lichte Tag ist also knapp 5–10 Minuten länger als der Tagbogen der Sonne, und das Phänomen Mitternachtssonne erscheint auch, wenn die Sonne nur teilweise oberhalb des Horizonts entlangwandert, also noch etwa einen Breitengrad südlich des Polarkreises. Noch etwas südlicher davon geht die Sonne zwar unter, aber die bürgerliche Dämmerung erstreckt sich auf den ganzen Zeitraum bis zum Aufgang – das wird als Weiße Nacht bezeichnet.
- Siehe auch: Erdbahn – zum Jahresumlauf der Erde um die Sonne bzw. Sonnenbahn – dem scheinbaren Umlauf der Sonne um den Standpunkt des Beobachters.
Mondaufgang und Monduntergang

Der Mond bleibt in seiner täglichen Bewegung durchschnittlich etwa 50 Minuten hinter der Sonne zurück, dies ist aber stark von der Position auf seiner elliptischen Umlaufbahn abhängig. Außerdem variiert seine Deklination im Laufe eines tropischen Monats um den Wert der Inklination von etwa 5°.
Daher verschieben sich die Auf- und Untergangszeiten entsprechend. Die Länge eines „Mond-Tags“ (von einem Aufgang bis zum darauffolgenden) kann zwischen etwa 24 h 15 min und 25 h 10 min schwanken. Weil er im Mittel 24 Stunden 48 Minuten dauert, gibt es jeden synodischen Monat einmal einen Kalendertag, an dem der Mond nicht aufgeht, und einen, an dem er nicht untergeht. Unter speziellen Umständen (etwa relativ hoch im Norden) kann der Mond sogar zweimal an einem Tag auf- oder untergehen.[3]
Satelliten
Die Sichtbarkeit von Satelliten ist etwa für die satellitengestützte Positionsbestimmung entscheidend, da deren Messgenauigkeit in direktem Zusammenhang steht mit der Zahl der Satelliten, die gerade über dem Horizont stehen. Daher muss die Anzahl der insgesamt in das System eingebundenen Satelliten so gewählt werden, dass für jeden Ort des abgedeckten Bereichs der Erdoberfläche möglichst immer, wenn ein Satellit „untergeht“, ein anderer auch „aufgeht“ und diesen ersetzt, sowie die Zahl der sichtbaren Satelliten nie unter vier absinkt. Näheres hierzu siehe im Abschnitt Aufbau und Funktionsweise der Ortungsfunktion in Global Positioning System sowie Galileo (Satellitennavigation).
- Siehe auch: Satellitenbahnelement – mit Grundlagen zur Sichtbarkeit von Satelliten
Kometen
Bei Kometen kommt neben der schnell ändernden Bahnposition als dominanter Faktor die stark ändernde Helligkeit, also die visuelle Sichtbarkeit (Freisichtigkeit) zum Tragen.
Der tatsächliche Aufgang

Die folgenden Erläuterungen gelten analog auch für den tatsächlichen Untergang.
Horizont
Der oben genannte dritte Faktor (Natürlicher Horizont) hat – außer am Meer und in der Ebene – den entscheiden Einfluss auf den Termin: Der tatsächliche Aufgang findet erst statt, wenn sich das Objekt über den Landschaftshorizont erhebt.
Im Gebirge beträgt die Winkeldistanz zwischen mathematischem und tatsächlichem Aufgang oft etliche Grad, der Zeitabstand geht also in die Stunden und kann in ungünstiger Lage auch dazu führen, dass die Sonne in manchen Tälern im Winter gar nicht aufgeht. Daher ist Sonnenseite und Schattenseite ein zentraler Aspekt der Siedlungsgeografie und beeinflusst auch die Waldgrenze und andere mikroklimatische Aspekte sowie über die Erosion auch viele Geländeformationen.
Auf dem Meer tritt – für größere Höhe über dem Meeresspiegel – wegen der Erdkrümmung an Stelle des Landschaftshorizonts die Kimmtiefe, durch welche die Sichtbarkeit von Gestirnen um einige Minuten verlängert wird. Den Einfluss der Kimmtiefe auf die Zeitpunkte wird – für den Fall hinreichend großer Krümmung – höchst anschaulich am Planeten von Saint-Exupérys Kleinen Prinzen dargestellt: Auf seinem kleinen Planeten reicht es, den Sessel etwas weiter zu stellen, um einen neuerlichen Sonnenuntergang zu erleben.
Auf den – in einer niederen Erdumlaufbahn – kreisenden Raumstationen und Raumfähren tritt in etwa entsprechend der kurzen Umlaufzeit ein Aufgang etwa alle 1½ Stunden ein.
Erdatmosphäre
Großen Einfluss hat die Astronomische Refraktion der Erdatmosphäre, die ein horizontnahes Gestirn um etwa 0°34’ höher erscheinen lässt.[1] Im Gebirge ist zusätzlich das lokale Klima am Talboden bzw. auf einer Talschulter entscheidend.
In Horizontnähe wird das Licht jedes Gestirns abgeschwächt (Extinktion) und verfärbt, da es den längstmöglichen Weg durch die Erdatmosphäre zurücklegen muss. Je nach Wetterlage können Sonne und Mond mit einem Farbenspiel von Rot bis Gelb oder Violett verbunden sein, das mit der Lichtbrechung und mit Schwebstoffen (Aerosolen) zusammenhängt. Darüber hinaus kann das Gestirn bzw. der Mond- und Sonnenrand beim Auf/Untergang stark wallen, weil warme, bodennahe Luftschichten die astronomische Refraktion beeinflussen.
Berechnung
Nach der Formel erfolgt auch die Berechnung der mathematischen Auf- und Untergänge: Da die Höhe kaum implizit berechnet wird, ermittelt man die Höhe für den vermutlichen Zeitpunkt (etwa, bei fortlaufenden Ephemeridenrechnung, den des Vortags plus dem – oben erwähnten – mittleren Wert für die Tagesdifferenz), und bestimmt dann iterativ einen hinreichend genauen Wert, oder interpoliert zwischen die Werte einer Ephemeridentabelle. [4]
Für den tatsächlichen Aufgang benötigt man dann etwa tabellierte Werte für den Landschaftshorizont. Da dieser – im Allgemeinen – halbwegs stetig ist, ermittelt man den Azimut für den gefundenen Wert, löst in fortschreitender Näherung die Gleichung im Zeitintervall
mit
Oder man ermittelt direkt als zweidimensionale Iteration:
mit
- : Position im topozentrischen Koordinatensystem,
- : Scheinbare Winkelgeschwindigkeiten in Azimut und Höhe,
- : Zeitargument.
Die Berechnung eines Aufgangs alleine aus dem Ort des Beobachters gehört zu den aufwändigsten Leistungen der astronomischen Phänomenologie, ist aber heute – zumindest bis zum Stadium des mathematischen Aufgangs – in viele astronomische Programme implementiert oder interaktiv im Internet verfügbar.
Besondere Bedeutung hat die Berechnung des Tagbogens der Sonne für die Effektivitätsberechnung von Solaranlagen oder in der Architektur für eine Abschätzung des Sonneneinfalls (Sonnenstandsdiagramm) und ist in CAAD-Software als Lichtmodul implementiert.
Literatur
- The Astronomical Almanac for the year 2006, The Stationery Office, London 2004, ISBN 0-11-887333-4.
- Jean Meeus: Astronomical Algorithms, Willmann-Bell, Richmond 2000 (2nd ed., 2nd printing), ISBN 0-943396-61-1.
- MZMsoft (Hrsg.): Sonnenaufgang – Sonnenuntergang. In: Genaues Analemma mit EXCEL • Version 2.0. Kapitel 4. (Webbook)
- Karl Ramsayer: Geodätische Astronomie, Band IIa des Handbuchs der Vermessungskunde. J.B.Metzler-Verlag, Stuttgart 1969.
- Wolfgang Vollmann: Erscheinungen der täglichen Bewegung. In: Hermann Mucke (Hrsg.): Moderne astronomische Phänomenologie. 20. Sternfreunde-Seminar, 1992/93. Zeiss Planetarium der Stadt Wien und Österreichischer Astronomischer Verein 1992, S. 185–196.
Weblinks
- Zur Berechnung siehe Weblinks in Ephemeride
Einzelnachweise
- Vollmann, A.2.1, S. 2
- Comparative Lengths of Longest Day and Longest Night, and of Shortest Day and Shortest Night. Astronomical Applications Department. U.S. Naval Observatory. (29. Sept. 2007)
- Vollmann, S. 8 gibt ein Beispiel für 23. Juli 1989, 66° Nord
- Vollmann, B.6, S. 9f