Mondfinsternis

Während einer Mondfinsternis (österreichisch Mondesfinsternis)[1] durchquert der Mond den Schatten, den die von der Sonne beleuchtete Erde in den Weltraum wirft. Dieses astronomische Ereignis kann nur eintreten, wenn Sonne, Erde und Mond hinreichend genau auf einer Linie liegen. Von der Erde aus gesehen stehen sich Sonne und Mond gegenüber. Es ist Vollmond, und von der Erde aus ist die Mondfinsternis überall dort zu sehen, wo der Mond zurzeit über dem Horizont steht bzw. wo Nacht ist.

Fotomontage von Aufnahmen der totalen Kernschattenfinsternis vom 28. August 2007 (rechts länger belichtete Aufnahmen)

Schema des Verlaufs der totalen Kernschattenfinsternis vom 28. August 2007 im Stundenabstand

Kern- und Halbschatten der Erde
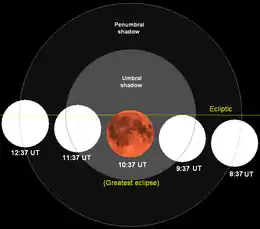
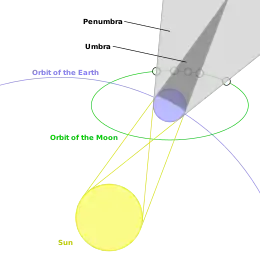
(nicht maßstabsgetreu)

Deutlich wahrzunehmen ist dieses Ereignis, wenn der Mond nicht nur durch den ringförmigen Halbschatten der Erde läuft, sondern ganz oder teilweise auch durch den kreisförmigen inneren Kernschatten. Umgangssprachlich ist mit Mondfinsternis i. d. R. eine Kernschattenfinsternis gemeint. Halbschattefinsternisse sind wenig auffällig und werden nur in der Astronomie mitgezählt. In beiden Fällen wird zwischen totalen und partiellen Finsternissen unterschieden, je nachdem, ob der Mond ganz oder nur teilweise in den jeweiligen Schatten eintaucht.

Die Mondbahnebene ist gegenüber der Ekliptik (Bahnebene der Erde um die Sonne) geneigt. Es gibt nur zwei Momente pro Umlauf, in denen sich der Mond mit der Sonne und der Erde in der Ekliptikebene befindet. Innerhalb weniger Stunden vor oder nach Vollmond tritt das nur bei jedem sechsten, manchmal auch bei einem fünften Vollmond ein. Pro Jahrhundert ereignen sich im Durchschnitt etwa 154 Kernschattenfinsternisse. Halbschattenfinsternisse finden etwa 88-mal pro Jahrhundert statt.

Grundlagen

Entstehung von Mondfinsternissen

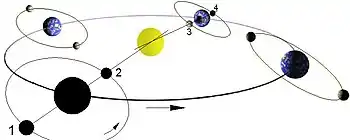
Konstellationen für Mond- und Sonnenfinsternisse (Erdbahn als großer Kreis, Mondbahn als kleine Kreise):
Eine Mondfinsternis kann bei den Mondstellungen 1 und 4, eine Sonnenfinsternis bei 2 und 3 entstehen.
(nicht maßstabsgetreu, Neigung der Mondbahn vergrößert)

Bei Vollmond steht der Mond in Opposition zur Sonne. Er befindet sich dabei meist nicht in der Ebene der Umlaufbahn der Erde um die Sonne (Ekliptik), da die Ebene der Umlaufbahn des Mondes reichlich 5° gegenüber der Ekliptik geneigt ist. Nur wenn der Mond zu Vollmond einem der beiden gedachten Schnittpunkte von Ekliptikebene und Mondbahn, Mondknoten genannt, hinreichend nahe ist, ereignet sich eine Mondfinsternis.

Von einer Mondfinsternis bis zum folgenden Vollmond vergeht rund ein synodischer Monat als mittlere Dauer einer Lunation. In manchen Fällen kann sich nun wieder eine Mondfinsternis ereignen, in den meisten Fällen jedoch nicht, da der Abstand zum Mondknoten zu groß ist. Der Mond durchläuft dann den Knoten nicht mehr zu Vollmond, und die sogenannte Knotenlinie – die gedachte Verbindung zwischen den beiden Mondknoten – ist daher nicht mehr auf die Sonne gerichtet. Somit findet bei diesem Umlauf des Mondes keine Finsternis statt. Beim sechsten Vollmond in Folge aber hält sich der Mond wieder recht nahe bei einem der Knoten auf, diesmal dem anderen, und somit ist eine Finsternis möglich. Sie findet statt, sofern der Abstand zum Knoten wieder so gering ist, dass eine gewisse Knotendistanz, das Finsternis-Limit genannt, unterschritten wird.

Nach den sechs Lunationen, die mit etwa 177 Tagen etwas weniger als ein halbes Jahr dauern, hat die Erde also noch nicht die Hälfte ihrer Bahn (oder 180°) absolviert. Auch der Gegenknoten liegt nach dieser Zeit nicht genau gegenüber der Ausgangsstellung, denn die Knotenlinie hat sich leicht gegenläufig gedreht und zeigt schon nach etwa 173 Tagen (ein halbes Finsternisjahr) wieder zur Sonne.

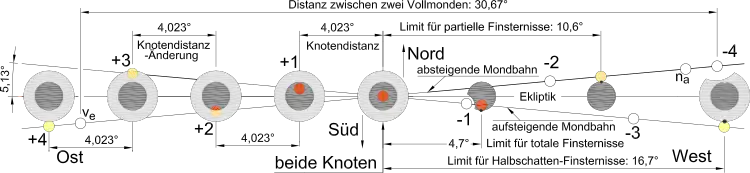
Semester-Zyklus aus neun Mondfinsternissen (−4 bis +4)

Bezogen auf die Knotenpassage ist der Vollmond mithin nach sechs Mondphasenzyklen um etwa vier Tage verspätet, und der Knotenabstand hat sich um einen Betrag von etwa 4° (auf der Ekliptik gemessen) verändert. Wenn die Distanz gemessen zum Knotenpunkt größer als 4,7° geworden ist, befindet sich der Mond nicht mehr total innerhalb des Kernschattens, es kann aber zu einer partiellen Kernschattenfinsternis kommen. Über etwa 10,6° Knotendistanz läuft der Mond nicht mehr durch den Kernschatten und es sind nur noch Halbschattenfinsternisse möglich, jenseits von etwa 16,7° befindet er sich auch außerhalb des Halbschattens.

Mit einer unauffälligen Finsternis durch den Halbschatten hört somit ein solcher Zyklus von knapp halbjährlich einander folgenden Finsternissen auf und ein Semester-Zyklus – mit der Finsternisperiode von etwa 177 Tagen der Basis-Zyklus aller Finsterniszyklen – ist beendet. Manchmal aber liegt gegen Ende eines Semesterzyklus – wie in der Abbildung dargestellt – schon der um eine Lunation frühere Vollmond innerhalb des (westlichen) Finsternis-Limits. Mit dieser Finsternis hat dann bereits ein neuer Semesterzyklus begonnen. Dessen nächste Finsternis findet fünf Lunationen nach der letzten Finsternis des vorherigen Zyklus statt.

Bei den ersten Finsternissen eines Zyklus nähert sich der Vollmond dem Knoten sukzessive, erreicht den kleinsten Abstand (als auffälligstes Ereignis) und entfernt sich wieder, bis das östliche Finsternis-Limit überschritten und der Zyklus zu Ende ist. Ein Semesterzyklus enthält 8 bis 10 Mondfinsternisse und dauert um die vier Jahre, wobei er sich mit anderen Semesterzyklen überschneiden kann. Mehr als die Hälfte der Ereignisse ist auffällig, zu Anfang und Ende eines Zyklus finden unauffällige Halbschattenfinsternisse statt.

Sichtbarkeit

Im Unterschied zur Sonnenfinsternis ist eine Mondfinsternis von jedem Ort auf der Nachtseite der Erde aus zu sehen und bietet – abgesehen von der relativen Lage zum Horizont – auch überall den gleichen Anblick. Lokal gesehen, auf einen festen Ort bezogen, ist daher eine Mondfinsternis weitaus häufiger zu beobachten als eine Sonnenfinsternis. Global betrachtet, auf die Erdkugel als ganze bezogen, kommen Sonnenfinsternisse allerdings häufiger vor als die auffälligen Mondfinsternisse im Kernschatten der Erde.

Selbst für eine totale Mondfinsternis sind der genaue Zeitpunkt des Eintritts und des Austritts in bzw. aus dem Kernschatten mit einer irdischen Perspektive nicht exakt vorhersagbar. Nicht nur ist der Kernschattenrand unscharf und vom angrenzenden Halbschatten nicht leicht abzugrenzen, ein verbleibender feiner Randstreifen im Halbschatten wäre mit bloßem Auge von der Erde aus nicht sichtbar.

Schwierigkeiten der Vorausberechnung

Die Voraussage von Finsternisterminen gehört zu den schwierigeren astronomischen Aufgaben, da bei der Bahnbestimmung der Himmelskörper Erde und Mond zahlreiche Einflüsse zu berücksichtigen sind, die periodisch schwanken oder sich in langen Zeiträumen verändern und sich als Bahnstörungen auswirken. Wegen der gegenseitigen Beeinflussung der Körper ist eine exakte Lösung für dieses Mehr-Körper-Problem nicht möglich, sondern nur eine Approximation durch numerische Verfahren der Modellierung. Inwieweit diese Annäherungen zutreffen, kann anhand von Beobachtungsdaten bestätigt beziehungsweise verbessert werden.

Der Schattenwurf der Erde stimmt zudem nicht genau mit dem geometrischen Modell überein, da die Sonne auch außerhalb ihrer als „Sonnenscheibe“ erscheinenden Photosphäre eine gewisse veränderliche Helligkeit hat (siehe Sonnenkorona und Protuberanz). Auch die Brechung des Sonnenlichts in der Erdatmosphäre wird bei der Berechnung vernachlässigt.

Arten von Mondfinsternissen

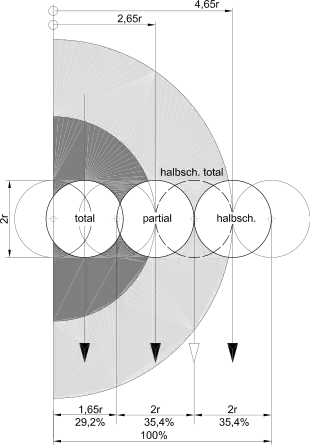
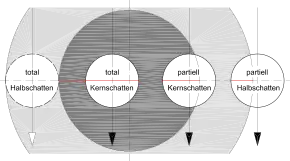
Arten von Mondfinsternissen und ihre hypothetische relative Häufigkeit, wenn Mondbahn und Erdbahn kreisförmig wären, bei Halbschattenradius = 4,65 Mondradien und Kernschattenradius = 2,65 Mondradien

Nach der Tiefe des Eintauchens in den Erdschatten in der Phase der größten Verdunkelung des Mondes werden Kernschatten- von Halbschattenfinsternissen unterschieden, und dabei jeweils totale von partiellen.

Totale Kernschattenfinsternis

Totale Kernschattenfinsternis
(27. September 2015)

Tritt der Mond während der Finsternis vollständig („total“) in den Kernschatten der Erde ein, so handelt es sich um eine totale Kernschattenfinsternis, auch totale Mondfinsternis genannt. Das durch die Luftschichten der Erdatmosphäre fallende Sonnenlicht wird nach innen gebrochen, wobei vor allem die kurzwelligen blauen Anteile durch Streuung geschwächt werden. Daher wird der Mond auch im Kernschatten der Erde noch von den langwelligen roten Anteilen erreicht und bleibt schwach sichtbar. Der Anblick des während einer Kernschattenfinsternis braun-rötlich verdunkelten Mondes wird umgangssprachlich auch Kupfermond oder Blutmond genannt. Die maximal mögliche Dauer einer totalen Mondfinsternis beträgt etwa 106 Minuten.[2]

Zentrale (Kernschatten-)Finsternis

Berührt der Mond nicht nur den Kernschatten, sondern auch die zentrale Linie des Kernschattens, spricht man von einer zentralen Finsternis. Dabei handelt es sich immer um eine totale Kernschattenfinsternis, da der Durchmesser des Mondes immer deutlich kleiner als der Radius des Kernschattens ist.

Partielle Kernschattenfinsternis

Partielle Kernschattenfinsternis
(16. August 2008)

Tritt der Mond während der Finsternis nur teilweise („partiell“) in den Kernschatten der Erde ein, handelt es sich um eine partielle Kernschattenfinsternis. Teile des Mondes bleiben also während der gesamten Finsternisdauer außerhalb des Kernschattens; sie befinden sich entweder im Halbschatten oder sind bei schmalem Halbschatten (Mond in Erdnähe) auch überhaupt nicht verfinstert.

Der Rand des von der Erde geworfenen Kernschattens wird dabei auf der Mondoberfläche abgebildet. Wie auch zu Anfang und Ende einer totalen Kernschattenfinsternis wird die Kernschattengrenze als eine gebogene Linie sichtbar. Bereits die Griechen der Antike interpretierten das als Schattenwurf der Erde und schlossen aus ihrem kreisförmigen Schatten, dass die Erde eine Kugel sei.

Totale Halbschattenfinsternis

Schematischer Verlauf einer totalen Halbschattenfinsternis
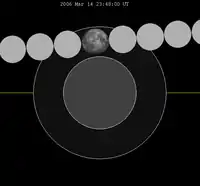
(14. März 2006)

Tritt der Mond während der Finsternis vollständig in den Halbschatten der Erde ein, ohne im Verlauf den Kernschatten zu berühren, handelt es sich um eine totale Halbschattenfinsternis. Dabei ist der dem Kernschatten zugewandte Teil des Mondes merklich dunkler als dessen abgewandter Teil. Totale Halbschattenfinsternisse sind selten, da der Ring des Halbschattens selbst im günstigsten Fall nur maximal 11 Prozent breiter als der Durchmesser des Mondes ist und der Mond nahezu passend durch den Halbschatten ziehen muss. Die letzte totale Halbschattenfinsternis fand am 14. März 2006 statt, die nächste wird am 29. August 2053 stattfinden.[3]

Ist der Halbschatten schmaler als der Durchmesser des Mondes, kann keine totale Halbschattenfinsternis auftreten, es sind nur partielle Halbschatten- oder partielle Kernschattenfinsternisse möglich. In sehr seltenen Fällen (wie am 25. April 2013) kann es passieren, dass selbst in der Phase der maximalen Bedeckung sich der Mond gleichzeitig teilweise im Kernschatten, im Halbschatten und außerhalb des Schattens befindet.

Partielle Halbschattenfinsternis

Partielle Halbschattenfinsternis
(10. Januar 2020)

Tritt der Mond während der Finsternis nur teilweise in den Halbschatten der Erde ein, handelt es sich um eine partielle Halbschattenfinsternis. Der Mond wird dabei kaum merklich verdunkelt. Erst ab einer penumbralen Magnitude von 0,7 wird mit freiem Auge eine Verfinsterung der dem Kernschatten zugewandten Seite sicher erkennbar.[3] Partielle Halbschattenfinsternisse des Mondes sind relativ häufig. Da dessen Durchmesser annähernd so groß wie der Ring des Halbschattens der Erde breit ist, tritt sie etwa genauso häufig wie partielle Kernschattenfinsternisse auf.

Häufigkeit

Im über mehrere Jahrhunderte gemittelten Durchschnitt sind Halbschattenfinsternisse ungefähr halb so häufig wie Kernschattenfinsternisse (37 Prozent bzw. 63 Prozent; etwa 88 bzw. 154 Ereignisse pro Jahrhundert). Kernschattenfinsternisse treten etwas weniger oft als totale denn als partielle Finsternisse auf (29 Prozent bzw. 34 Prozent aller Mondfinsternisse; etwa 70 bzw. 84 Ereignisse pro Jahrhundert).[3]

Im 21. Jahrhundert sind allerdings deutlich mehr totale (85) als partielle (57) Kernschattenfinsternisse zu erwarten,[3] denn der Mond durchläuft in diesem Jahrhundert häufiger als im Durchschnitt bei Vollmond nahe der Erde deren breiteren Schatten.

Kenngrößen

Magnitude der Finsternisarten
(rot gezeichnete Strecke je im Verhältnis zum Monddurchmesser).

Magnitude (oder Größe)

Die Magnitude oder Größe einer Mondfinsternis ist ein Maß für die Eindringtiefe des Mondes in den Erdschatten. Auf einer durch die Mitte des Schattens und die Mondmitte gelegten Geraden wird der Abstand gemessen zwischen dem schattenzentrumnäheren Mondrand und dem mondnäheren Schattenrand. Der zum Monddurchmesser ins Verhältnis gesetzte Messwert stellt die Magnitude der Finsternis dar.

Für Kernschattenfinsternisse wird das Eindringen in den Kernschatten (lat. umbra) gemessen. Im Mittel ist der Kernschattendurchmesser etwa 2,63 mal so groß wie der Monddurchmesser; bei diesem Verhältnis kann die umbrale Magnitude zwischen 0 und 1,815 variieren. Werte zwischen 0 und 1 kennzeichnen eine partielle, Werte ab 1 eine totale Finsternisform.

Für Halbschattenfinsternisse wird das Eindringen in den Halbschatten (lat. penumbra) gemessen. Das Verhältnis von Halbschattenbreite und Monddurchmesser beträgt im Mittel um die 1,03. Bei einer partiellen Halbschattenfinsternis liegt die penumbrale Magnitude zwischen 0 und 1. Werte ab 1 kennzeichnen eine totale Halbschattenfinsternis; sie kann nur eintreten, wenn der Halbschatten mindestens so breit wie der Mond ist.

Danjon-Skala

Totale Kernschattenfinsternisse lassen sich auch durch die Helligkeit und Färbung des Kernschattens infolge des von der Erdatmosphäre gebrochenen Lichtes charakterisieren. Abhängig vom Verschmutzungsgrad der Atmosphäre (insbesondere der Stratosphäre) zeigen sich Unterschiede, zum Beispiel können nach explosiven vulkanischen Eruptionen mit starkem Ascheausstoß dunkle oder sehr dunkle Finsternisse auftreten. André Danjon hat folgende einfache Skala vorgeschlagen, um die beobachtete Helligkeit (als Parameter L) zu kennzeichnen, die nach ihm benannte Danjon-Skala:

L = 0: sehr dunkle Finsternis; Mond fast unsichtbar, besonders in der Mitte der Totalität

L = 1: dunkle Finsternis; graue oder bräunliche Färbung; Details der Mondoberfläche nur schwierig erkennbar

L = 2: tiefrote oder rostrote Finsternis, mit einem sehr dunklen Zentrum, aber relativ hellem Rand des Kernschattens

L = 3: ziegelrote Finsternis, gewöhnlich mit einem hellen oder gelblichen Rand des Kernschattens

L = 4: sehr helle kupferrote oder orange Finsternis mit einem sehr hellen bläulichen Kernschattenrand.

Berechnung

Abstand des Mondes vom Mittelpunkt des Erdschattens

Eine wesentliche Größe zur Beschreibung einer Mondfinsternis ist der üblicherweise als Winkeldistanz (Sehwinkel) angegebene Abstand des Mondes vom Mittelpunkt des Erdschattens. Scheitelpunkt des Sehwinkels ist der Mittelpunkt der Erde.[4] Bezugsachse ist die von der Sonne durch den Mittelpunkt der Erde zum Mittelpunkt des Erdschattens führende Gerade. Sie ist die Polachse des zur Darstellung des Sehwinkels als Referenzsystem verwendeten sphärischen Koordinatensystems.

Ausgangsgrößen der Berechnung[5][6] sind die äquatorialen Winkelkoordinaten (Ephemeriden) der Sonne und des Mondes, deren Rektaszension $\alpha$ und Deklination $\delta \!\,$ .

Die positive Seite der Polachse zeigt in Richtung zum Mond (weg von der Sonne, hin zur Gegensonne). Somit ergeben sich die äquatorialen Winkelkoordinaten $a$ und $d$ der Polachse aus den Ephemeriden der Sonne wie folgt:

a=\alpha _{s}+180^{\circ }\quad {\text{und}}\quad d=-\delta _{s}\,.

Bei der Transformation zwischen Winkelkoordinaten werden in einem Zwischenschritt die jeweiligen kartesischen Koordinaten ineinander umgerechnet. Da nur der zusammenfassende Sehwinkel zu ermitteln ist, kann bereits die Resultierende aus der x- und der y-Koordinate des Mondes im Referenzsystem (z-Achse = Polachse) gebildet und daraus sofort der Sehwinkel errechnet werden. Die Richtungen der x- und y-Achse sind in diesem Fall beliebig. Im Folgenden ist die y-Achse in der Äquatorebene verblieben. Sie zeigt nach Osten, und die x-Achse ergänzt ein Rechtssystem:

{\begin{aligned}x&=\sin \delta _{m}\cos d-\cos \delta _{m}\sin d\cos \left(\alpha _{m}-a\right)\,,\\y&=\cos \delta _{m}\sin \left(\alpha _{m}-a\right)\,.\end{aligned}}

Diese kartesischen Koordinaten sind auf den Abstand $1$ zwischen Erde und Mond normiert.

Der gesuchte Sehwinkel $\sigma$ für den Abstand des Mondes vom Mittelpunkt des Erdschattens ist:

\sigma \approx \sin \sigma ={\sqrt {x^{2}+y^{2}}}\,.

Berechnung von x und y

Zur Berechnung werden die äquatorialen Koordinaten des Einheitsvektors zur Mondposition und die Drehmatrix für die Koordinatendrehung aus dem äquatorialen ins Bezugs-System benötigt und miteinander multipliziert:

Mond-Einheitsvektor: [7]

{\begin{aligned}{\begin{pmatrix}X\\Y\\Z\\\end{pmatrix}}&={\begin{pmatrix}\cos \delta _{m}\cdot \cos \alpha _{m}\\\cos \delta _{m}\cdot \sin \alpha _{m}\\\sin \delta _{m}\\\end{pmatrix}}\end{aligned}}\,.

Drehmatrix: [8]

{\begin{aligned}D&={\begin{pmatrix}\sin \delta _{s}\cdot \cos \alpha _{s}&\sin \delta _{s}\cdot \sin \alpha _{s}&-\cos \delta _{s}\\\sin \alpha _{s}&-\cos \alpha _{s}&0\\\dots &\dots &\dots \end{pmatrix}}\end{aligned}}\,.

Multiplikation:

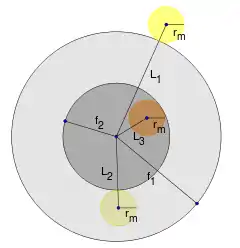
{\begin{aligned}{\begin{pmatrix}x\\y\\z\\\end{pmatrix}}&=D\cdot {\begin{pmatrix}X\\Y\\Z\\\end{pmatrix}}\end{aligned}}\,.

Sehwinkel der Schattenradien f_i und der Kontakte L_i

Radien des Erdschattens und Sehwinkel für Kontakte

Die Radien $f_{2}$ und $f_{1}$ von Kern- und Halbschatten können ebenfalls als Sehwinkel angegeben werden. Sie werden als Konstante betrachtet, da sich die Abstände zwischen Sonne, Erde und Mond während einer Finsternis fast nicht ändern. Zusammen mit dem Mondradius $r_{m}$ (ebenfalls als Sehwinkel angegeben) lassen sich diejenigen Abstände $\sigma _{i}$ ( $L_{i}$ in nebenstehender Skizze) des Mondes vom Mittelpunkt des Erdschattens berechnen, die die Kontakte des Mondes mit den Schattenrändern kennzeichnen:

L_{1}=f_{1}+r_{m}

Ein- und Austritt des Mondes in aus den Halbschatten

L_{2}=f_{2}+r_{m}

Ein- und Austritt des Mondes in aus den Kernschatten

L_{3}=f_{2}-r_{m}

Beginn und Ende der totalen Finsternis

Aus einer in engen Zeitintervallen berechneten Reihe von Positionen des Mondes im Erdschatten lassen sich die zu den vorgegebenen Sehwinkeln $L_{i}$ gehörenden Kontaktzeiten interpolieren.

Berechnung von $f_{2}$ und $f_{1}$

Geometrie des Kernschattens[5]

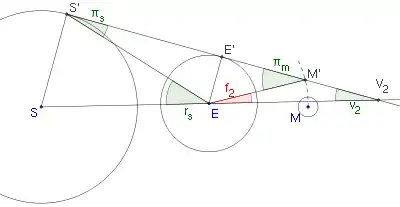
Als Parallaxen $\pi _{s}$ und $\pi _{m}$ angegebenen Entfernungen der Sonne und des Mondes von der Erde sind Sehwinkel. Ebenfalls als Sehwinkel $r_{s}$ ist der Radius der Sonne angegeben.

Aus dem Dreieck EM'V₂ folgt

f_{2}=\pi _{m}-v_{2}

,

und aus dem Dreieck ES'V₂ folgt

v_{2}=r_{s}-\pi _{s}

.

Dann ist:

f_{2}=\pi _{s}+\pi _{m}-r_{s}

.

$f_{1}$ ist mithilfe einer analogen Skizze[5] (die Sonne und Erde tangierenden Randlinien des Halbschattens kreuzen sich zwischen Sonne und Erde im Punkt V₁) und mit analogem Rechnen zu ermitteln.

Durch die Wirkung der Erdatmosphäre sind die tatsächlichen Radien des Kern- und des Halbschattens gegenüber einer rein geometrischen Berechnung vergrößert, was bei einer Berechnung der Kontakzeiten durch eintsprechende Korrekturen in den astronomische Elementen entsprechend zu berücksichtigen ist.

Astronomische Elemente

Die Größen $x\!\,$ , $y\!\,$ , $\sigma \!\,$ , $L_{1}\!\,$ , $L_{2}\!\,$ , $L_{3}\!\,$ , $f_{1}\!\,$ und $f_{2}\!\,$ sind astronomische Elemente, die gelegentlich[5] auch „Besselsche Elemente einer Mondfinsternis“ genannt werden. Zu den vorwiegend bei der Behandlung von Sonnenfinsternissen in einem Zwischenschritt formulierten Besselschen Elementen besteht aber nur ein rechnerisch formaler und kein sachlicher Zusammenhang. Dieser besteht auch nur bei zwei von in beiden Fällen acht astronomischen Elementen: Die Ausdrücke für die Elemente x und y haben als Ergebnis einer Koordinatentransformation nur die gleiche Grundform, und das jeweils zugehörende Koordinatensystem ist nicht identisch mit dem anderen.

Optische Effekte während einer Mondfinsternis

Rötliche Farbe

Der bei einer totalen Finsternis vollständig im Kernschatten der Erde liegende Mond ist noch schwach als rötlich gefärbter Blutmond erkennbar. Ursache ist, dass das Sonnenlicht, das den Mond erreicht, einen teilweise mehrere hundert Kilometer langen Weg durch die Erdatmosphäre hinter sich hat. Durch Rayleigh-Streuung an den Molekülen der Erdatmosphäre werden die kurzwelligen blauen Anteile vom weißen Sonnenlicht deutlich stärker in andere Richtungen gestreut als die langwelligen roten Anteile. Dadurch besteht das die Erdatmosphäre passierende Licht fast nur noch aus rötlichen Anteilen. Durch die Atmosphäre wird das Sonnenlicht um maximal 2,2° nach innen abgelenkt[9] (siehe auch terrestrische Refraktion). Daher dringt es teilweise in den Kernschatten der Erde ein und trifft somit auch auf die Mondoberfläche.

Die folgenden Abbildungen zeigen dasselbe Bild einer Mondfinsternis beim Austritt aus dem Kernschatten in den drei Primärfarben Rot, Grün und Blau. Im vom direkten weißen Sonnenlicht getroffenen Bereich links haben alle drei Primärfarben eine hohe Intensität. Nach rechts, in Richtung Kernschattenzentrum, nimmt die Intensität bei allen drei Farben ab. Die rechte Mondhälfte wird allerdings kaum noch von blauem Licht erreicht, und das grüne Licht ist im rechten Mondviertel äußerst schwach. Im Kernschatten sind also praktisch fast ausschließlich die roten Lichtanteile vorhanden, die für die Namensgebung eines Blutmondes ursächlich sind.

Mondfinsternis in den drei Primärfarben Rot, Grün und Blau
Farbbild (Farbtemperatur 4100 Kelvin)
Roter Lichtanteil
Grüner Lichtanteil
Blauer Lichtanteil

Helligkeit

Bei einer zentralen Finsternis nimmt die scheinbare visuelle Helligkeit des Mondes von etwa −12^m,5 auf etwa +2^m um etwa den Faktor 600 000 ab. Im Zentrum des Kernschattens beträgt die Abnahme der Intensität (die Helligkeitsabnahme, die ein Beobachter auf der Mondoberfläche feststellen würde) sogar 1 bis 2 Millionen, rund hundertmal mehr als bei einer totalen Sonnenfinsternis.

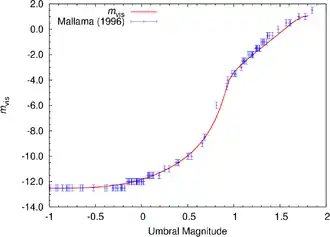
Theoretische Lichtkurve m_vis einer Mondfinsternis in Abhängigkeit von der Magnitude (zum Vergleich Messdaten von Mallama)

Die Mondfinsternisse der vergangenen Jahre waren überwiegend hell, um L = 3, was auf eine verhältnismäßig saubere Stratosphäre schließen lässt. Nach dem Ausbruch des Vulkans Pinatubo im Jahr 1991 wurden teilweise sehr dunkle Finsternisse beobachtet. Bei einer solchen Finsternis kann die Mondhelligkeit bis auf etwa +5^m abfallen, entsprechend einem Faktor von 10 Millionen. Um etwa denselben Faktor nimmt auch die Intensität im Zentrum ab; die untere Grenze wird durch das Licht der Korona der Sonne bestimmt, die durch die Erde nur teilweise verdeckt wird. Somit ermöglicht die Farbe und Helligkeit des verfinsterten Mondes Rückschlüsse auf die Reinheit der Erdatmosphäre. Heute ist diese Methode jedoch überholt, da Messungen von Satelliten oder Flugzeugen aus viel genauere Informationen über Verunreinigungen der Luft liefern als die reine optische Abschattung dies erlaubt.

Vergrößerung des Erdschattens

unscharfer, diffus verwaschener Kernschattenrand bei der Finsternis im Juli 2018, 21:19 UTC nach Ende der Totalität

Ein weiterer interessanter Effekt ist die Erdschattenvergrößerung. Wer schon eine Mondfinsternis teleskopisch verfolgt hat, wird unschwer festgestellt haben, dass die Kontaktzeiten oft von den gerechneten Werten abweichen. In der Tat erscheint der Schattenkegel der Erde wegen der Atmosphäre etwa 2 Prozent größer, ein Effekt, auf den bereits Philippe de La Hire im frühen 18. Jahrhundert hinwies. Der Kernschattenrand erscheint nicht scharf, sondern diffus verwaschen.

Fotografische Aufnahme

Eine fotografische Aufnahme des Mondes im Kernschatten stellt wegen der geringen Leuchtdichte eine vergleichsweise anspruchsvolle Aufgabe dar. Je nach Aufnahmebedingungen liegt der Belichtungswert deutlich unter 1 EV.

Je größer der Höhenwinkel des Mondes bei der Aufnahme ist, desto geringer sind atmosphärische Störungen, die dazu führen, dass Konturen in den Bildern verwaschen werden. Gleichermaßen nimmt auch die Lichtabschwächung durch die Extinktion in der Erdatmosphäre mit zunehmendem Abstand vom Horizont ab.[10]

Entfernungseinstellung

In der Praxis kann das Objektiv wegen der sehr großen Entfernung in der Regel auf „unendlich“ eingestellt werden. Da der Mond sehr weit entfernt ist, muss das Objektiv für Aufnahmen, die von Menschen betrachtet nicht als unscharfes Bild empfunden werden sollen, mindestens auf die hyperfokale Distanz eingestellt werden. In diesem Fall werden alle Objekte zwischen der halben hyperfokalen und unendlicher Distanz hinreichend scharf abgebildet. Bei Bildern, die technisch ausgewertet oder von denen Ausschnitte verwendet werden sollen, muss die Entfernung entsprechend den Anforderungen gegebenenfalls noch genauer eingestellt werden.

Belichtungszeit

Wenn die Kamera mit der Erdoberfläche bewegt wird, verschiebt sich der Bildort des Mondes mit der Zeit, so dass sich im Bild eine Bewegungsunschärfe ergibt. Dies kann kompensiert werden, indem die Kamera mit einer geeigneten Vorrichtung um die Erdachse mitgedreht wird. Alternativ können auch bewegliche Bildsensoren zu diesem Zweck eingesetzt werden (siehe zum Beispiel „Astro Tracer“ der Pentax K-1).[11]

Ansonsten muss die maximale Belichtungszeit $t_{\mathrm {max} }$ so weit begrenzt werden, dass die Bewegungsunschärfe nicht erkennbar ist. Bei vorgegebenem Bildwinkel $\alpha$ in Grad kann dafür die folgende Faustformel angewendet werden, um die maximale Belichtungszeit in Sekunden abzuschätzen:[12]

t_{\mathrm {max} }={\frac {\alpha }{6}}

Bei einer feststehenden, omnidirektionalen Kamera (Bildwinkel = 360°) sind somit Aufnahmen mit einer Belichtungszeit von einer Minute möglich, wenn keine vergrößerten Bildausschnitte verwendet werden sollen. Formatfüllende (quadratische) Aufnahmen des Mondes mit einem diagonalen Bildwinkel von 0,7° können jedoch nur mit einer Belichtungszeit von gut einer Zehntelsekunde aufgenommen werden, wenn die Kamera während der Aufnahme nicht mitbewegt wird.

Bei digitalen Steh- und Bewegtbildaufnahmen mit längeren Belichtungszeiten ist zu beachten, dass sich der Bildsensor im Betrieb erwärmt und das Bildrauschen mit steigender Temperatur deutlich zunimmt. Ferner nimmt bei vielen Bildsensoren, wie zum Beispiel Active Pixel Sensoren, das Bildrauschen mit der Belichtungszeit zu. Für eine Bilderzeugung mit hohem Signal-Rausch-Verhältnis kann der Bildsensor passiv oder aktiv gekühlt werden. Ansonsten können mehrere Bilder mit begrenzter Belichtungszeit aufgenommen und später softwaretechnisch zusammengefügt werden („Stacking“, siehe unten). Zu kurze Belichtungszeiten erzeugen aufgrund der vielen Einzelaufnahmen allerdings vermehrtes Ausleserauschen, so dass ein Kompromiss gefunden werden muss.[13]

Blendenzahl

Da sehr wenig Licht zur Verfügung steht, empfiehlt es sich, möglichst kleine Blendenzahlen und somit große Blendenöffnungen zu wählen, damit für die Aufnahme möglichst viel Licht eingefangen werden kann.

Da die Abbildungsqualität von optischen Systemen bei großer Öffnungsweite durch Abbildungsfehler begrenzt wird, ist es empfehlenswert, optische korrigierte Objektive oder Teleskope einzusetzen, wie zum Beispiel Asphären zur Reduktion der sphärischen Aberration oder Apochromaten zur Reduktion der chromatischen Aberration. Der Farbquerfehler kann bei modernen digitalen Kamerasystemen automatisch kompensiert werden.

Farbtemperatur

Die Farbtemperatur kann bei Farbaufnahmen entsprechend dem weiß-neutralen Wert des vom Vollmond reflektierten Lichtes auf zirka 4100 Kelvin eingestellt werden. Höhere Werte, wie zum Beispiel der Wert für das direkte Sonnenlicht von 5500 Kelvin, ergeben Bilder mit stärkerem roten Anteil, der der subjektiven Assoziation zur Farbe von Blut häufig näher kommt.

Stacking

Um die Lichtausbeute zu erhöhen, können mit Bildsensoren Serienbilder aufgenommen werden, die anschließend softwaremäßig deckungsgleich übereinandergelegt und zusammengesetzt werden (englisch: „stacking“). Dies hat den Vorteil, dass jedes einzelne Bild hinreichend frei von Bewegungsunschärfe sowie von mit der Belichtungszeit anwachsenden Signalstörungen ist, aber dennoch deutlich mehr Licht für die zusammengesetzte Aufnahme zur Verfügung steht. Dadurch ergibt sich ein deutlich besseres Signal-Rausch-Verhältnis und somit weniger Bildrauschen sowie ein größerer Dynamikumfang.

Mondfinsternisse

Totale Mondfinsternisse zwischen 1900 und 2100 ab 100 Minuten Dauer

Datum	Dauer	Datum	Dauer	Datum	Dauer
4. Aug. 1906	1h 41m	6. Jul. 1982	1h 46m	26. Jun. 2029	1h 42m
16. Jul. 1935	1h 40m	16. Jul. 2000	1h 46m	7. Jul. 2047	1h 40m
26. Jul. 1953	1h 41m	15. Jun. 2011	1h 40m	17. Jun. 2076	1h 41m
25. Jun. 1964	1h 41m	27. Jul. 2018	1h 43m	28. Jun. 2094	1h 41m

Das Datum gibt jeweils den Tag an, auf den die Mitte der Finsternis in Weltzeit fällt.

Alle Mondfinsternisse der Jahre 2014 bis 2020

Datum	Art	Größe		Eintritt		Beginn Totalität	Maxi- mum	Ende Totalität	Austritt		Sichtbarkeit 10° östl. Länge	siehe
Datum	Art	p	u	Halb	Kern	Beginn Totalität	Maxi- mum	Ende Totalität	Kern	Halb	Sichtbarkeit 10° östl. Länge	siehe
15. Apr. 2014	Kern, total	2,318	1,291	04:53	05:58	07:06	07:47	08:24	09:33	10:37	nicht sichtbar	[14]
8. Okt. 2014	Kern, total	2,146	1,166	08:15	09:14	10:25	10:55	11:24	12:34	13:33	nicht sichtbar	[15]
4. Apr. 2015	Kern, total	2,079	1,001	09:01	10:15	11:57	12:01	12:02	13:44	14:58	nicht sichtbar	[16]
28. Sep. 2015	Kern, total	2,230	1,276	00:11	01:07	02:11	02:47	03:23	04:27	05:22	komplett	[17]
23. Mrz. 2016	Halb, part.	0,775	−0,312	09:39	11:48					13:54	nicht sichtbar	[18]
16. Sep. 2016	Halb, part.	0,908	−0,064	16:54	18:55					20:53	bei Mondaufgang	[19]
11. Feb. 2017	Halb, part.	0,988	−0,035	22:34	00:45					02:53	vollständig	[20]
7. Aug. 2017	Kern, part.	1,288	0,246	15:50	17:23	18:21			19:18	20:51	bei Mondaufgang	[21]
31. Jan. 2018	Kern, total	2,294	1,316	10:51	11:48	12:52	13:31	14:08	15:11	16:08	nicht sichtbar	[22]
27. Jul. 2018	Kern, total	2,679	1,609	17:15	18:24	19:30	20:23	21:13	22:19	23:29	bei Mondaufgang	[23]
21. Jan. 2019	Kern, total	2,168	1,195	02:36	03:34	04:41	05:13	05:43	06:51	07:48	vollständig	[24]
16. Jul. 2019	Kern, part.	1,704	0,653	18:44	20:02	21:32			23:00	00:18	vollständig	[25]
10. Jan. 2020	Halb, part.	0,896	−0,116	17:07	19:11					21:12	bei Mondaufgang	[26]
5. Jun. 2020	Halb, part.	0,908	−0,405	16:54	18:55					20:54	bei Mondaufgang	[27]
5. Jul. 2020	Halb, part.	0,355	−0,644	03:07	04:31					05:52	vollständig	[28]
30. Nov. 2020	Halb, part.	0,828	−0,262	07:32	09:44					11:53	nicht sichtbar	[29]

17. Juli 2019, 00:32 in Spanien

part.: partielle, total: totale, Kern: Kernschatten, Halb: Halbschatten
Uhrzeiten in UTC (Mitteleuropäische Zeit: MEZ = UTC + 1h; Mitteleuropäische Sommerzeit: MESZ = UTC + 2h)

Alle Mondfinsternisse des letzten und des aktuellen Jahrhunderts[30][31][32]

Siehe auch

Literatur

Jean Meeus, Hermann Mucke: Canon der Mondfinsternisse −2002 bis +2526. 3. Auflage. Astronomisches Büro, Wien 1992
Fred Espenak: Thousand Year Canon of Lunar Eclipses 1501 to 2500. Astropixels Publishing, Portal 2014, ISBN 978-1-941983-03-4 (online)

Weblinks

Commons: Mondfinsternis – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Mondfinsternis – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Mondfinsternis.info – deutschsprachige Informationen, sehr ausführlich zu jeder Finsternis
„Frag' den Sterngucker – Wann kommt es zu einer Mondfinsternis?“ – Video mit erklärender Animation
frei skalierbare Skizze von Sonne, Erde und Mond sowie Kern- und Halbschatten der Erde
NASA – Lunar Eclipse Page (englisch)
Robert Harry van Gent: A Catalogue of Eclipse Cycles. In: Webpages on the History of Astronomy. 8. September 2003, abgerufen am 4. Oktober 2008 (englisch, Zusammenstellung aller Zyklen in den Serien der Finsternisse).
Mondfinsternis beim Bayerischen Rundfunk Wissen – ausführliche Informationen zur jeweils nächsten Mondfinsternis in Deutschland mit Grafiken, Fotos und Erklärvideo

Einzelnachweise

Eintrag Mondesfinsternis in Duden (online).
J. Meeus: More Mathematical Astronomy Morsels, Willmann-Bell Inc., 2002, Kap.24 ISBN 0-943396-74-3
J. Meeus, H. Mucke: Canon der Mondfinsternisse -2002 bis +2526, 3. Auflage, S. XXVI. Astronomisches Büro, Wien, 3. Auflage 1992.
Dass der Scheitel des Sehwinkels bei Beobachtung von der Erdoberfläche aus ein anderer ist, bedeutet einen vernachlässigbaren Unterschied.
P. Kenneth Seidelmann: Explanatory Supplement to the Astronomical Almanac, 2nd ed. 1992 Seite 467–470 und 428–430
Siegfried Wetzel: Mondfinsternis und Besselsche Elemente? online
Die kartesischen Koordinaten X, Y und Z des Mond-Einheitsvektors werden mit $r=r_{m}=1$ erhalten.
Die erste Drehung erfolgt um die alte Z-Achse mit $\gamma =a=\alpha _{s}+\pi$ .
Die zweite Drehung erfolgt um die neue y-Achse mit $\beta =\pi -d=\pi +\delta _{s}$ .
Die Drehung um die neue z-Achse entfällt: $\alpha =0$ .
Jerome Meyer, Dissertation Uni Bremen, 2004 online, Abb. 6.5, Wert verdoppelt
Atmosphärische Störungen, Wikibook „Digitale bildgebende Verfahren“, Kapitel „Bildaufnahme“, abgerufen am 31. Juli 2018
Kamera Pentax K-1: Spiegelreflexkamera für hohe Ansprüche, test.de vom 3. August 2016, abgerufen am 31. Juli 2018
Maximale Belichtungszeit, Wikibook „Digitale bildgebende Verfahren“, Kapitel „Bildaufnahme“, abgerufen am 31. Juli 2018
Sensor-Rauschen, Stemmer Imaging, abgerufen am 3. August 2018
NASA: Total Lunar Eclipse of 2014 Apr 15. (PDF; 52 kB) Abgerufen am 16. Dezember 2012.
NASA: Total Lunar Eclipse of 2014 Oct 08. (PDF; 52 kB) Abgerufen am 16. Dezember 2012.
NASA: Total Lunar Eclipse of 2015 Apr 04. (PDF; 50 kB) Abgerufen am 5. Januar 2015.
NASA: Total Lunar Eclipse of 2015 Sep 28. (PDF; 52 kB) Abgerufen am 5. Januar 2015.
NASA: Penumbral Lunar Eclipse of 2016 Mar 23. (PDF; 43 kB) Abgerufen am 5. Januar 2015.
NASA: Penumbral Lunar Eclipse of 2016 Sep 16. (PDF; 44 kB) Abgerufen am 5. Januar 2015.
NASA: Lunar Eclipse of 2017 Feb 11. (PDF) Abgerufen am 1. November 2017 (englisch).
NASA: Lunar Eclipse of 2017 Aug 07. (PDF) Abgerufen am 1. November 2017 (englisch).
NASA: Lunar Eclipse of 2018 Jan 31. (PDF) Abgerufen am 1. November 2017 (englisch).
NASA: Lunar Eclipse of 2018 Jul 27. (PDF) Abgerufen am 1. November 2017 (englisch).
NASA: Lunar Eclipse of 2019 Jan 21. (PDF) Abgerufen am 1. November 2017 (englisch).
NASA: Lunar Eclipse of 2019 Jul 16. (PDF) Abgerufen am 1. November 2017 (englisch).
NASA: Penumbral Lunar Eclipse of 2020 Jan 20. (PDF) Abgerufen am 1. November 2017 (englisch).
NASA: Penumbral Lunar Eclipse of 2020 Jun 05. (PDF) Abgerufen am 1. November 2017 (englisch).
NASA: Penumbral Lunar Eclipse of 2020 Jul 05. (PDF) Abgerufen am 1. November 2017 (englisch).
NASA: Penumbral Lunar Eclipse of 2020 Nov 30. (PDF) Abgerufen am 1. November 2017 (englisch).
NASA Eclipse Web Site
NASA: Lunar Eclipses: 2011–2020. Abgerufen am 10. Dezember 2011.
NASA: Lunar Eclipses: 2001–2010. Abgerufen am 10. Dezember 2011.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Duden-1] Eintrag Mondesfinsternis in Duden (online).

[MeeusMorselsIIKap24-2] J. Meeus: More Mathematical Astronomy Morsels, Willmann-Bell Inc., 2002, Kap.24 ISBN 0-943396-74-3

[MeeusMuckeCanon-3] J. Meeus, H. Mucke: Canon der Mondfinsternisse -2002 bis +2526, 3. Auflage, S. XXVI. Astronomisches Büro, Wien, 3. Auflage 1992.

[4] Dass der Scheitel des Sehwinkels bei Beobachtung von der Erdoberfläche aus ein anderer ist, bedeutet einen vernachlässigbaren Unterschied.

[seid-5] P. Kenneth Seidelmann: Explanatory Supplement to the Astronomical Almanac, 2nd ed. 1992 Seite 467–470 und 428–430

[6] Siegfried Wetzel: Mondfinsternis und Besselsche Elemente? online

[7] Die kartesischen Koordinaten X, Y und Z des Mond-Einheitsvektors werden mit $r=r_{m}=1$ erhalten.

[8] Die erste Drehung erfolgt um die alte Z-Achse mit $\gamma =a=\alpha _{s}+\pi$ .
Die zweite Drehung erfolgt um die neue y-Achse mit $\beta =\pi -d=\pi +\delta _{s}$ .
Die Drehung um die neue z-Achse entfällt: $\alpha =0$ .

[9] Jerome Meyer, Dissertation Uni Bremen, 2004 online, Abb. 6.5, Wert verdoppelt

[10] Atmosphärische Störungen, Wikibook „Digitale bildgebende Verfahren“, Kapitel „Bildaufnahme“, abgerufen am 31. Juli 2018

[11] Kamera Pentax K-1: Spiegelreflexkamera für hohe Ansprüche, test.de vom 3. August 2016, abgerufen am 31. Juli 2018

[12] Maximale Belichtungszeit, Wikibook „Digitale bildgebende Verfahren“, Kapitel „Bildaufnahme“, abgerufen am 31. Juli 2018

[13] Sensor-Rauschen, Stemmer Imaging, abgerufen am 3. August 2018

[14] NASA: Total Lunar Eclipse of 2014 Apr 15. (PDF; 52 kB) Abgerufen am 16. Dezember 2012.

[15] NASA: Total Lunar Eclipse of 2014 Oct 08. (PDF; 52 kB) Abgerufen am 16. Dezember 2012.

[16] NASA: Total Lunar Eclipse of 2015 Apr 04. (PDF; 50 kB) Abgerufen am 5. Januar 2015.

[17] NASA: Total Lunar Eclipse of 2015 Sep 28. (PDF; 52 kB) Abgerufen am 5. Januar 2015.

[18] NASA: Penumbral Lunar Eclipse of 2016 Mar 23. (PDF; 43 kB) Abgerufen am 5. Januar 2015.

[19] NASA: Penumbral Lunar Eclipse of 2016 Sep 16. (PDF; 44 kB) Abgerufen am 5. Januar 2015.

[20] NASA: Lunar Eclipse of 2017 Feb 11. (PDF) Abgerufen am 1. November 2017 (englisch).

[21] NASA: Lunar Eclipse of 2017 Aug 07. (PDF) Abgerufen am 1. November 2017 (englisch).

[22] NASA: Lunar Eclipse of 2018 Jan 31. (PDF) Abgerufen am 1. November 2017 (englisch).

[23] NASA: Lunar Eclipse of 2018 Jul 27. (PDF) Abgerufen am 1. November 2017 (englisch).

[24] NASA: Lunar Eclipse of 2019 Jan 21. (PDF) Abgerufen am 1. November 2017 (englisch).

[25] NASA: Lunar Eclipse of 2019 Jul 16. (PDF) Abgerufen am 1. November 2017 (englisch).

[26] NASA: Penumbral Lunar Eclipse of 2020 Jan 20. (PDF) Abgerufen am 1. November 2017 (englisch).

[27] NASA: Penumbral Lunar Eclipse of 2020 Jun 05. (PDF) Abgerufen am 1. November 2017 (englisch).

[28] NASA: Penumbral Lunar Eclipse of 2020 Jul 05. (PDF) Abgerufen am 1. November 2017 (englisch).

[29] NASA: Penumbral Lunar Eclipse of 2020 Nov 30. (PDF) Abgerufen am 1. November 2017 (englisch).

[30] NASA Eclipse Web Site

[31] NASA: Lunar Eclipses: 2011–2020. Abgerufen am 10. Dezember 2011.

[32] NASA: Lunar Eclipses: 2001–2010. Abgerufen am 10. Dezember 2011.