Geometrische Modellierung
Geometrische Modellierung, auch englisch Computer-Aided Geometric Design (CAGD) genannt, bezeichnet die computergestützte Beschreibung der Form geometrischer Objekte. Sie beschäftigt sich sowohl mit der Beschreibung von zweidimensionalen Kurven als auch von dreidimensionalen Flächen und Körpern. Die geometrische Modellierung findet in der Computergrafik, im Computer-Aided Design (CAD), bei der Methode der Finiten Elemente und anderen ingenieurtechnischen und wissenschaftlichen Bereichen Anwendung.

Freiformkurven und -flächen

Freiformkurven und -flächen lassen sich mittels Splines, hier gemeint also stückweise polynomiale Funktionen, beschreiben. Das Prinzip kann von den zweidimensionalen Kurven auf dreidimensionale Flächen erweitert werden.
Hermite-Kurven
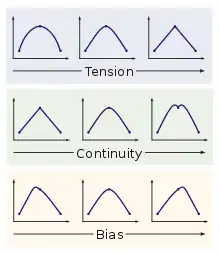
Kubisch Hermitesche Kurven sind aus hermiteschen Polynomen dritten Grades zusammengesetzt. Jedes Polynom wird dabei durch einen Anfangs- und Endpunkt sowie den entsprechenden Tangenten bestimmt. Wenn die hermiteschen Polynome zu einem Spline zusammengesetzt werden, werden die Tangenten zweier aneinander liegenden Polygone gleichgesetzt. Für die Wahl der Tangenten gibt es verschiedene Möglichkeiten. Die einfachste besteht darin, eine Tangente mit der die nächsten Kontrollpunkte verbindenden Geraden gleichzusetzen, es wurden jedoch noch andere Methoden entwickelt:
- Bei Cardinal Splines werden die Tangenten durch einen Parameter c zwischen 0 und 1 bestimmt, der die „Spannung“ am Kontrollpunkt angibt.
- Catmull-Rom-Splines sind ein Spezialfall der Cardinal Splines, wobei c=0 ist. Sie werden oft in der Computeranimation als Animationskurven verwendet, da sie genau durch die Kontrollpunkte verlaufen und ihre Ableitung stetig ist.
- Kochanek-Bartels-Splines, auch TCB-Splines genannt, bieten eine weitere Parametrisierung von Hermite-Kurven mit den drei Parametern Tension, Continuity und Bias.
Bézierkurven
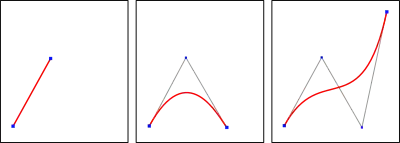
Eine Bézierkurve n-ten Grades ist eine parametrische Kurve, die durch n+1 Kontrollpunkte definiert wird. Das Polygon, das die Kontrollpunkte miteinander verbindet, wird als Kontrollpolygon bezeichnet. Während eine lineare Bézierkurve, also eine Bézierkurve ersten Grades, ein einfaches Segment zwischen den beiden Kontrollpunkten ist, beschreibt eine quadratische Bézierkurve einen Parabelteil. Viele Grafikprogramme verwenden kubische Bézierkurven.
Eine Bézierkurve interpoliert zwischen den einzelnen Kontrollpunkten mittels Bernsteinpolynomen, die den Einfluss der Kontrollpunkte in Abhängigkeit vom Kurvenparameter angeben. Abgesehen vom Anfangs- und Endpunkt verläuft die Kurve im Allgemeinen nicht durch die Kontrollpunkte, sondern ist in deren konvexer Hülle enthalten. Zur Zeichnung einer Bézierkurve kann der De-Casteljau-Algorithmus verwendet werden, der eine Bézierkurve durch einen Polygonzug annähert.
Bézierkurven sind invariant unter affinen Abbildungen. Das bedeutet, dass eine affine Abbildung der Kontrollpunkte die gleiche Kurve wie eine affine Abbildung der Originalkurve ergibt. Ein Problem von Bézierkurven ist, dass bei bestimmter Lage der Kontrollpunkte Berühr- oder Doppelpunkte möglich sind. Lokale Änderungen an den Kontrollpunkten wirken sich zwar unerwünschterweise auf die gesamte Kurve aus, sind jedoch nur lokal von Bedeutung.
B-Spline-Kurven und NURBS

B-Spline-Kurven bieten eine im Vergleich zu Bézierkurven verbesserte Lokalität und Kontrollierbarkeit: Änderungen wirken sich nur lokal aus, und nur ein Teil der Kurve muss neu berechnet werden. Ähnlich wie Hermite-Kurven sind B-Spline-Kurven stückweise aus einzelnen Polynomen zusammengesetzt. Die Nahtstellen werden Knotenpunkte genannt. Unerwünschte Oszillationen (Runges Phänomen) bei einer großen Zahl von Knotenpunkten werden so vermieden. B-Spline-Kurven sind eine linear gewichtete Kombination von Basisfunktionen, genannt B-Splines.[1] Die Basisfunktionen sind stückweise Polynome mit einem kleinen Träger. Änderungen außerhalb des Trägers wirken sich nicht auf die B-Spline-Kurve aus.
Uniforme Basisfunktionen sind verschobene, jeweils auf einem Knotenpunkt zentrierte Kopien voneinander. Bei uniformen, linearen Basisfunktionen handelt es sich um Dreieckfunktionen, die an einem bestimmten Knotenpunkt zentriert sind und einen Träger haben, der über drei Knotenpunkte reicht. Quadratische und kubische Basisfunktionen sind aus entsprechend höheren Polynomen zusammengesetzt, aber stets über einem Knotenpunkt zentriert. Im Gegensatz dazu haben nichtuniforme Basisfunktionen unterschiedliche Formen. B-Spline-Kurven können mit dem De-Boor-Algorithmus in einen Polygonzug umgewandelt werden.
Eine Erweiterung sind rationale B-Spline-Kurven oder im Allgemeinen Non-Uniform Rational B-Splines (NURBS), deren Parameterdarstellung ein mathematischer Bruch ist. NURBS sind allgemein genug, um alle üblichen Kurven und Flächen zu beschreiben. Einige neuere Modellierungswerkzeuge verwenden sie als alleinige interne Repräsentationsmethode.
Darstellungsschemata
Es wurden verschiedene Methoden zur Repräsentation von Körpern (Darstellungsschemata) entwickelt, die sich durch ihre Speicheranforderungen, numerische Präzision, Komplexität und Fähigkeit, in andere Darstellungsschemata umgewandelt werden zu können, unterscheiden. Eine weitere Eigenschaft eines Darstellungsschemas ist die Möglichkeit, überprüfen zu können, ob ein Modell korrekt ist, also ein „echtes“, physikalisch mögliches Objekt definiert.
Man unterscheidet zwischen direkten Darstellungsschemata, die das Volumen selbst beschreiben, und indirekten Schemata, bei denen die Beschreibung über Kanten und Oberflächen erfolgt. Außerdem sind Hybridschemata denkbar, die beide Methoden kombinieren.
Normzellen-Aufzählungsschema
Beim Normzellen-Aufzählungsschema wird der Raum in ein gleichmäßig aufgeteiltes Gitter aus Zellen (Voxel) aufgeteilt. Ein Körper wird durch eine Menge von Zellen dargestellt. Je kleiner die Voxel sind, desto besser wird der Körper angenähert. Das Aufzählungsschema verbraucht sehr viel Speicherplatz.
Constructive Solid Geometry
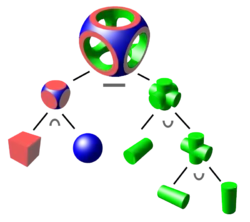
Bei Constructive Solid Geometry (CSG) werden Objekte mit Hilfe von Grundkörpern wie Kugel, Quader oder Zylinder sowie Operatoren wie Schnitt, Vereinigung oder Differenz modelliert. Ein CSG-Körper lässt sich anhand einer Formel, die die Operatoren auf Grundkörper anwendet, beschreiben und als Baum veranschaulichen.
CSG ist besonders im CAD-Bereich gebräuchlich. Eine Untersuchung kam zu dem Ergebnis, dass sich 63 % aller mechanischen Bauteile mit einem CSG-System, das nur Quader und gerade Kreiszylinder verwendet, modellieren lassen. Wenn mehr Grundkörper zugelassen werden, so lassen sich 90 % aller Bauteile im klassischen Maschinenbau (vorrangig Bohren, Fräsen, Drehen der Bauteile oder ihrer Gussformen) auf natürliche Weise per CSG beschreiben.[2]
Ein großer Vorteil von CSG gegenüber anderen Darstellungsschemata ist, dass ihre Korrektheit garantiert ist, sofern nur bestimmte Grundkörper zugelassen werden. Wenn beispielsweise R-Sets als Grundkörper verwendet werden, so garantieren deren Eigenschaften, dass ein entsprechender CSG-Baum korrekt ist. Außerdem sind CSG-Körper sehr kompakt und einfach zu erzeugen. Viele Rendermethoden können jedoch nicht direkt mit CSG umgehen und verlangen, dass CSG-Körper zunächst in B-reps umgewandelt werden, was eine vergleichsweise schwierige Aufgabe ist.
Bis in die 1980er Jahre basierten die meisten Modellierungswerkzeuge entweder auf Boundary Representations oder auf CSG.
Generative Modellierung
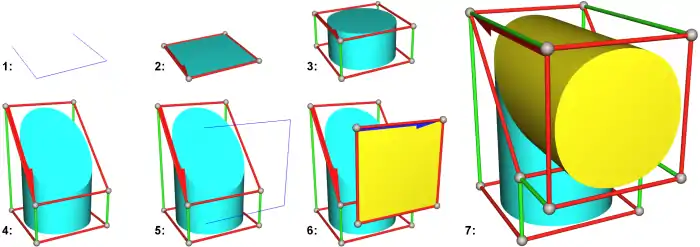
Ein generatives Modell ist eine Form, die durch eine kontinuierliche Transformation einer Form, Generator genannt, erzeugt wurde. Die Dimension des Modells spielt dabei keine Rolle. Die Modellierung findet auf hohem Niveau statt und ist erweiterbar. Mit Hilfe einer Programmiersprache wie der Generative Modelling Language kann der Anwender recht einfach eine Bibliothek nützlicher Formen aufbauen.
Verschiebegeometrien, auch Sweeps genannt, sind ein Spezialfall generativer Modelle. Sie werden erzeugt, indem eine Kurve oder ein Volumen entlang einer Kurve geführt wird.
Ein Spezialfall von Sweeps sind Rotationsflächen, die erzeugt werden, indem eine bestimmte Menge um eine beliebige Achse rotiert wird.
Voxelgitter
Voxelgitter sind räumlich und gitterförmig angeordnete Werte, die die „Dichte“ eines Objektes beschreiben und mit den Mitteln der Volumengrafik dargestellt werden können. Voxelgitter ermöglichen es, Teile von Objekten „wegzuschneiden“ und ins Innere zu sehen. Auch CSG-Operationen sind leicht realisierbar. Allerdings benötigen Voxelgitter sehr viel Speicherplatz, und sie neigen zu unerwünschten Aliasing-Effekten. Der erhöhte Speicherbedarf kann in manchen Anwendungsfällen durch Verwendung von Octrees reduziert werden. Die Modellierung mittels Voxelgitter findet vor allem in der Medizin, Fluiddynamik und bei der Darstellung natürlicher Objekte wie Wolken Anwendung.
Drahtgittermodell
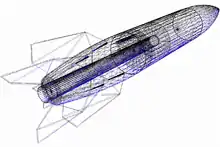
Ein Drahtgittermodell definiert einen Körper ausschließlich über seine Kanten. Dieses Modell bietet Geschwindigkeitsvorteile, da die Darstellung sehr effizient ist. Ein Problem mit diesem Schema ist seine Mehrdeutigkeit. Ein Drahtgittermodell kann mehrere verschiedene Körper repräsentieren, da nicht klar ist, wo die Oberflächen verlaufen. Eine Verdeckungsberechnung wie bei Oberflächen ist daher nicht möglich, allerdings kann der Haloed-Line-Algorithmus angewandt werden.
Oberflächendarstellung
Eine Oberflächendarstellung, auch Boundary Representation oder B-rep genannt, ist die Beschreibung eines Körpers anhand seiner Oberfläche; B-reps sind also „hohl“. B-reps sind das wahrscheinlich am häufigsten verwendete Darstellungsschema in der Computergrafik.[3] Insbesondere Polygonnetze werden häufig verwendet.
B-reps eignen sich gut zum effizienten Rendern allgemeiner Oberflächen und erlauben es, lokale Änderungen am Modell vorzunehmen. Nachteile von B-reps sind ihre hohen Speicheranforderungen und die schwierige Überprüfung der Korrektheit.
Auf sogenannten Euler-Operationen basierende Darstellungsschemata werden dazu verwendet, bei der Modellierung von Körpern als B-rep die Korrektheit zumindest teilweise zu garantieren. Die Idee besteht darin, nur sogenannte Euler-Operationen zuzulassen, die die Euler-Charakteristik beibehalten oder sie in bestimmter Art und Weise verändern.
Modellierungstechniken
Polygonisierung
Viele Algorithmen in der Computergrafik, darunter einige Rendermethoden, arbeiten ausschließlich mit Polygonnetzen. Auch Finite-Elemente-Methoden basieren auf dieser Darstellungsform. Es wurden zahlreiche Polygonisierungsalgorithmen entwickelt, die Ergebnisse von unterschiedlicher Qualität liefern. Im Allgemeinen soll eine Polygonisierungsmethode eine gute Annäherung an die Form des Originalobjekts erzielen, Polygone mit ausgewogener, nicht zu schmaler Form produzieren, und die lokale Topologie des Originalobjekts respektieren, also keine Spalten oder Bruchstellen entstehen lassen. Beispiele von Polygonisierungsalgorithmen sind
- der cutting cube Algorithmus von M. Schmidt[4] und
- der Verfolgungsalgorithmus von E. Hartmann[5]. Siehe[6]
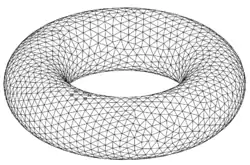
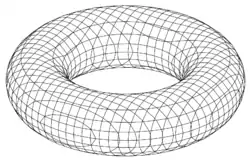
Physikalisch basierte Modellierung

Modellierungsmethoden, die zusätzlich zu den statischen auch die dynamischen Eigenschaften von Objekten berücksichtigen, nennt man physikalisch basiert. Objekte können dabei nicht nur starr, sondern auch flexibel sein. Ein Beispiel ist ein Stück Stoff, das über andere Objekte gelegt wird und dessen Faltenwurf automatisch berechnet wird.
Literatur
- Stephan Abramowski, Heinrich Müller: Geometrisches Modellieren. BI Wissenschaftsverlag, Mannheim 1991
- Max Agoston: Computer Graphics and Geometric Modeling: Implementation and Algorithms. Springer, London 2005, ISBN 1-85233-818-0
- Max Agoston: Computer Graphics and Geometric Modeling: Mathematics. Springer, London 2005, ISBN 1-85233-817-2
- Gerald Farin: Curves and Surfaces for Computer-Aided Geometric Design. Academic Press, San Diego 1997, ISBN 0-12-249054-1
- Josef Hoschek, Dieter Lasser: Grundlagen der geometrischen Datenverarbeitung. Teubner, Stuttgart 1992, ISBN 3-519-12962-0
- Michael Mortenson: Geometric Modeling. Industrial Press, New York 2006, ISBN 0-8311-3298-1
Weblinks
- Erich Hartmann: Geometry and Algorithms for CAD. (PDF; 2,87 MB) Lecture Note, 2003, TU Darmstadt
- Basics der Freiformgeometrie zur Klima- und Geländemodellierung. (PDF; ~700 kB) Summary, 2015, Vienna
Einzelnachweise und Anmerkungen
- Mit „B-Splines“ werden oft nicht nur die Basisfunktionen, sondern auch die aus ihnen zusammengesetzten B-Spline-Kurven bezeichnet. Hier werden zur Unterscheidung die Begriffe „Basisfunktionen“ beziehungsweise „B-Spline-Kurven“ verwendet.
- M. M. Samuel u. a.: Methodology and Results of an Industrial Parts Survey. In: Technical Memorandum 21, Production Automation Project, University of Rochester, New York 1976. Zitiert in Max Agoston: Computer Graphics and Geometric Modeling: Implementation and Algorithms, S. 169
- Max Agoston: Computer Graphics and Geometric Modeling: Implementation and Algorithms, S. 166
- M. Schmidt: Cutting Cubes - visualizing implicit surfaces by adaptive polygonization. Visual Computer (1993) 10, S. 101–115
- E. Hartmann: A marching method for the triangulation of surfaces, The Visual Computer (1998), 14, S. 95–108
- Geometry and Algorithms for COMPUTER AIDED DESIGN, S. 81