Farbraum

Alle Farben eines Farbmodells, die durch eine farbgebende Methode tatsächlich ausgegeben werden können, werden in dem dreidimensionalen Farbraum dargestellt. Jede farbgebende Methode hat ihren eigenen Farbraum. Eine Darstellung aller Farbörter (Singular: Farbort) eines Farbmodells bildet den Farbkörper.

Farbmodell, hier nach HSV

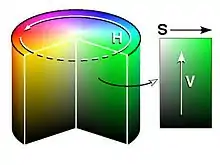
Alle Verfahrensweisen und damit verbundenen Geräte und Materialien, die Farbe zur Darstellung bringen können, werden farbgebende Methoden genannt. Solche Verfahren sind Drucker, Monitore, Ausbelichtungen, Kunstdrucke, Lackierungen oder manueller Farbauftrag.

Definitionen

Verschiedene Darstellungen von Farbmodellen und Farbräumen
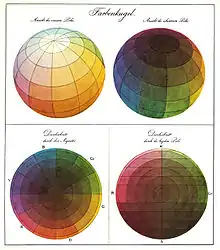Runges Farbenkugel 1810
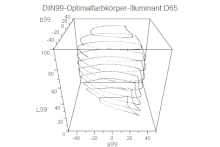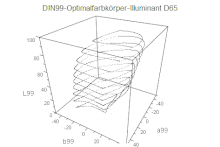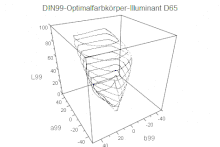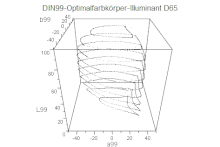Farbraumanimation
HSB-Modell: Änderung jeweils einer von drei notwendigen Variablen

Farbe

Farben, in der Farbmetrik genauer als Farbvalenz bezeichnet, beruhen auf Farbreizen, die sich durch ihre spektrale Zusammensetzung unterscheiden. Durch die Notwendigkeit, diese Unterschiede exakt definieren zu können, wurden verschiedene Farbmodelle entwickelt. Grundlage dafür sind die Graßmannschen Gesetze. Jede Farbe kann durch einen Farbnamen (beschreibende Worte), aber auch durch den numerischen Farbort definiert werden. Je nach Farbmodell kann nach Helligkeit, Sättigung und Farbton, aber auch nach Hell-/Dunkel-, Rot-/Grün- und Gelb/Blau-Wert mit drei derartigen Größen die Farbe eindeutig beschrieben sein.

Farbsystem

Ein Farbsystem ist die Systematik zur Anordnung der Farbvalenzen, die auf unterschiedliche Art Farben erzeugen: durch „Mischung“ von Licht als Lichtfarben oder die Verwendung von Farbmitteln auf einem Trägermaterial als Körperfarben. Je nach Anwendungszweck kann eine unterschiedliche Anzahl von Grundfarben genutzt werden: mindestens drei, aber auch vier oder mehr farbgebende Substanzen werden verwendet. Diese sind allerdings nicht mehr unabhängig voneinander.

Das Farbsystem stellt immer nur das Grundprinzip einer Farbmischung dar, nie die technische Umsetzung der farbgebenden Methode. Am deutlichsten wird das an der Farbe Weiß. Diese kann je nach verwendeter farbgebender Methode gleißend und blendend, aber auch matt und stumpf sein. Beide Arten, Weiß darzustellen, widersprechen nicht dem zugrunde liegenden Farbsystem.

Farbmodell

Das Farbmodell entsteht aus dem abstrakten Farbsystem meist dreidimensional für die praktische Darstellung, die unterschiedliche Formen haben kann. Innerhalb der Modelle sind allen Farben eindeutige Zahlenwerte, die Farborte, zugeordnet.

Wird der Farbort einer Farbe mit Hilfe einer Software innerhalb des gleichen Farbmodells geändert, so kann ein Informationsverlust entstehen. Auch durch den Übertragungsweg bis zur farbgebenden Methode entstehen diese Qualitätsverluste. Dies kann nicht verhindert, nur verringert werden. Die Anzahl der Differenzierungsstufen innerhalb des Farbmodells zu erhöhen und ein geeignetes Farbmanagement sind dabei am wirkungsvollsten. Das eingesetzte Farbmodell ist der Träger der Information der Schärfe und so beeinflusst wiederum das Modell das Ergebnis der Schärfe in der Fotografie.

Farbkörper

Der Farbkörper ist der geometrische Körper, mit dem sich das Farbmodell darstellen lässt. Für Philipp Otto Runge war es die Kugel, durch Erwin Schrödinger wurde der Farbkörper nach Siegfried Rösch angeregt, Wilhelm Ostwald wählte den Doppelkegel und Harald Küppers das Rhomboeder. Es ist eine systematische Anordnung im dichten, kontinuierlichen Zusammenhang aller Farbörter des zugrunde gelegten Farbsystems.

Farbort

Der Farbort (Plural: Farbörter, nicht Farborte)[1] liegt als Punkt im oder auf dem Farbkörper, und wird im Farbraum mit geeigneten Koordinaten in seiner Lage beschrieben. Dieser Ort repräsentiert die vereinbarte Farbe. Farbörter sind in Farbräumen kontinuierlich beschreibbar, ihre reale Präsentation in Farbatlanten ist dagegen naturgemäß nur diskontinuierlich möglich.

Farbraum

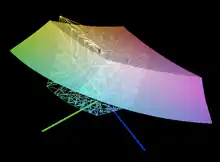
Bildschirm- und Druckmaschinen-Gamut im CIELAB-Farbraum

Der Farbraum einer farbgebenden Methode umfasst möglichst alle Farben, die innerhalb des Farbmodells darstellbar sind. Bei der Verwirklichung der Farbdarstellung sind zwangsläufig alle farbgebenden Methoden verlustbehaftet. Einige Farben haben zwar einen definierten Farbort, sind aber mit den verfügbaren Farbmitteln nicht darstellbar. Die darstellbaren Farben bilden innerhalb des Farbmodells einen Körper, auch als Gamut bezeichnet. Dieser Körper wird Farbraum genannt, der Farbraum kann im idealen Falle das ganze Farbmodell erfüllen. Farbräume dienen zur Visualisierung von Differenzen zwischen einem Idealzustand und der geforderten Realität.

Überblick

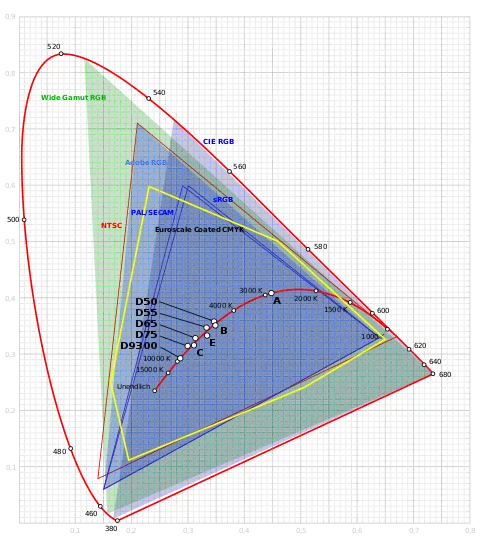
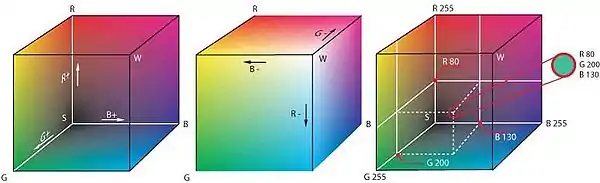
Die Lage einiger technischer Farbräume auf der xy-Chromazitätsebene

Die Menge der in einem Farbraum präsentierten Farben ist die Gesamtheit aller Farbreize, die vom Sehsinn wahrgenommen werden. So bildet beispielsweise die Menge der Farben, die an einem Bildschirm sichtbar sind, einen Farbraum, in diesem Falle den Geräte-Farbraum des Bildschirms mit den Koordinaten R(ot), G(rün) und B(lau).
Es können auch mehrere (materielle) Basisfarben den jeweils definierten und begrenzten Messraum dieser Farben aufspannen. Als Grundfarben eines Farbmodells dürfen nur solche Farbvalenzen gewählt werden, die nach den Graßmannschen Gesetzen als unabhängig voneinander definiert sind.
Farben werden durch ein Farbmodell quantifiziert. Ein Farbmodell ist ein Koordinatensystem mit Basiskoordinaten entsprechend den gewählten Farbvalenzen. Die Zahlenangaben sind Ortsvektoren des Farbmodells, ihre Angabe kann in Form eines Tupels (hier 3-Tupel) erfolgen.
Farbräume sind ein notwendiges Werkzeug in der Farbmetrik, bei der gerätebedingten Umwandlung von Reproduktionen und Design (Colormanagement) und Gegenstand verschiedener Farbenlehren. Ein Farbraum unterliegt als „Modell der Wirklichkeit“ den Grenzen seiner Definition.
Ziel der Gestaltung von Farbräumen ist, innerhalb der Modellgrenzen Übereinstimmung mit der Farbwahrnehmung des Menschen zu erreichen. Dabei müssen Eingabegerät und Ausgabegerät aufeinander abgestimmt werden. Durch verbesserte farbgebende Methoden entstehen wiederum neue Anforderungen an das Colormanagement.

Farbempfindung

Das menschliche Auge besitzt im Regelfall drei Zapfenarten, die als farbempfindliche Rezeptoren das Sehen „in Farbe“ ermöglichen. Die spektrale Empfindlichkeit der Zapfen deckt ihrerseits ein Teilintervall des sichtbaren Lichtes ab.

Das Farbensehen kann dreidimensional beschrieben werden. Diese Feststellung ist im 1. Graßmannschen Gesetz begründet, damit ist ein Farbraum (hier als Raum der Farben) dreidimensional. Die Ursache dafür ist die Reizintensität an den drei Farbrezeptoren. Die Farbvalenz (umgangssprachlich „die Farbe“) wird durch drei Vektorlängen zum Farbort dargestellt, einem Punkt im Farbraum. Die Dreidimensionalität war Kunstmalern schon lange bekannt und wurde von Thomas Young erstmals mit der Drei-Farben-Theorie beschrieben.

Bei der Nachstellung von Körperfarben ist eine spektralgerechte Wiedergabe kaum möglich, da unterschiedliche Materialien oder Gerätesysteme oder die verschiedenen farbgebenden Methoden kaum gleiche Eindrücke hinterlassen, zudem ist die (reale) Farbe von Umgebungsbedingungen beeinflusst. Durch das Phänomen der Metamerie wird beschrieben, dass Farben auf verschiedene Arten aus drei Grundfarben entstehen können. So können Farben mit drei Grundvalenzen für praktische Zwecke meist ausreichend genau dargestellt werden, solange die Bedingungen nicht zu stark verändert sind. Die Vielfalt der spektralen Zusammensetzungen wird für das Individuum auf drei wahrnehmende Zapfenwerte abgebildet.

Übertragung von additiv zu subtraktiv

Durch die selbstleuchtenden Eigenschaften der additiven Farbmischung entsteht ein hoher Kontrastumfang. Die „Strahlkraft“ dieser Luminanz vermittelt nicht nur einen hohen Schärfeeindruck, sondern lässt auch Farbdarstellungen zu, die nur durch additive Farbmischung möglich sind.

Bei der subtraktiven Farbmischung (Körperfarbe) können, weil andere Primärfarben benutzt werden, andere Farben als bei der additiven Farbmischung dargestellt werden. Die Farbräume von Geräten mit additiver und subtraktiver Farbemischung unterscheiden sich grundsätzlich. Beide beinhalten andererseits auch viele Farben, die sie gemeinsam darstellen können. Wegen dieser Gemeinsamkeiten ist eine Farbseparation überhaupt erst möglich.

Problematisch wird es, wenn die farbgebenden Methoden nicht mehr unter Normbedingungen betrachtet werden. Die subtraktive Farbmischung „lebt“ von reflektiertem Licht, während die additive Farbmischung selbstleuchtende Farben benutzt. Beide reagieren also anders auf die Änderung des Umgebungslichtes – hier kann auch das beste Farbmanagement (noch) nichts ausrichten.

Graues, von einem Tintenstrahldrucker auf Papier erzeugtes Zeichen

Ein häufiger Praxisfall für Farbseparation ist die Umrechnung von RGB-Daten (additiv, etwa vom Bildschirm) in das CMYK-System für den Druck (subtraktiv). Der Übergang von einer additiven zu einer subtraktiven Mischung erfolgt über eine einfache Transformation der Farbräume von Gerät zu Gerät, da das nichtlineare Mischverhalten der Druckpigmente ebenso wie die Farbe des Papieres (möglicherweise mit einem Farbstich) berücksichtigt werden müssen. Da die Farbabdeckung beim Druck nicht linear ist, wird die Farbraumumrechnung beträchtlich erschwert. Hierfür sind besondere Farbräume (ICC) oder für diesen Zweck erstellte LUT (look-up table) nötig.

Ein weiteres Problem dieser Umrechnung ist die Verwendung unterschiedlicher Farbmengen, drei oder vier Farben, oder mehr wie beim Einsatz von Schmuckfarben.

Schwarz wird zusätzlich im Druck meist aus folgenden Gründen eingesetzt (überdies steht mit Farbruß ein effektives Farbmittel zur Verfügung):

Soll auf subtraktiv mit einer farbgebenden Methode Schwarz oder dunkelgrau dargestellt werden, ist es wirtschaftlicher, Schwarz als gesonderte Farbe zu benutzen. Die Darstellung von Schwarz aus nur drei Farben ist auf Grund der tatsächlichen Absorption der Farbpigmente sehr aufwändig, teuer, teilweise unmöglich und wird daher (fast) nur bei der Farbfotografie benutzt.
Der subtraktiven Farbmischung fehlt der hohe Kontrastumfang, die der additiven Mischung eigen ist. Die Zugabe von Schwarz verbessert den subjektiven Kontrasteindruck (der Drucker spricht von Tiefe).
Da Druckverfahren rasterorientierte Verfahren sind, entstehen bei der Darstellung zarter Farben starke subjektive Schärfeverluste. Die Rasterweite vergrößert sich, dadurch enthält das Bilddetail weniger Informationen, das wird vom Auge als Schärfeverlust interpretiert. Durch die Zumischung von Schwarz entsteht ein subjektiver Ausgleich dieses Verlustes. Demgegenüber können zu druckende Grauwerte aus dem gleichen Grund oft besser aus zusammengesetzten Farben statt aus schwarz erzeugt werden.

Bedingt durch Probleme wie nichtlineares Farbverhalten, Farbmengenunterschiede, Luminanzverlust, subjektiver Schärfeausgleich ist eine Farbseparation sehr aufwendig.

Bei der Fotoreproduktion ist die Ausbelichtung im klaren Vorteil, da sie das gleiche Farbmodell (nämlich RGB) wie die Eingabegeräte (Scanner, Fotoapparat) und das Kontrollgerät (Bildschirm) benutzt. Lediglich für das fertige Foto (farbgebende Methode) muss die additive in die subtraktive Farbmischung übertragen werden.

Farbabstände und Gleichabständigkeit

Es existieren keine Geräte, die den kompletten Farbumfang der menschlichen Wahrnehmung erfassen oder erzeugen können. MacAdam arbeitete an einer Farbmetrik, die die Gleichabständigkeit von Farbabständen ermöglichen sollte, die Farbabstände sollen als visuell gleich empfunden werden. Eine solche Farbmetrik hat zur Folge, dass die Parameter für die Farbabstände von der Lage im Farbarten- oder Chromatizitätsdiagramm abhängig sind.

Die menschliche Wahrnehmung von Farbabständen in technisch definierten Farbräumen darzustellen ergibt im CIE-Farbraum Toleranzellipsen gleicher Farbwahrnehmung, bekannt als MacAdam-Ellipsen. Hier ist der Ansatzpunkt für die Weiterentwicklung der höheren Farbmetrik. Weiterführende Arbeiten auf diesem Gebiet wurden von Walter S. Stiles und D. Farnsworth geleistet. Stiles entwickelte ein Linienelement, dass gleichabständig wahrgenommene Farbabstände auch mathematisch gleichabständig (mit dem gleichen Abstand) beschreibt. Farnsworth entwickelte eine nichtlineare Transformation, die alle MacAdams-Ellipsen zu Kreisen verformt. Von der CIE wurde als Lösung zunächst der UCS-Farbraum in mehreren Versionen geschaffen. Später (1976) wurden sowohl der Lab-Farbraum (für Körperfarben bevorzugt) als auch der LUV-Farbraum (für Lichtfarben bevorzugt) als gleichabständige Farbräume präsentiert.

Geschichte

Runges Farbenkugel 1810

Beispiel eines modernen Farbraums: DIN99-Optimalfarbkörper in Schnittdarstellung. Schnittebenen von Helligkeit L₉₉=5 bis 95 in Zehnerschritten. a₉₉ liegt etwa gelb-blau Richtung von Runges Farbenkugel, b₉₉ stellt die rot-grüne Richtung dar. Eine entfernte Ähnlichkeit zu Runges Farbenkugel ist erkennbar. Die Verzerrungen kommen dadurch zustande, dass in modernen Farbräumen die Verknüpfung der Farben mit Helligkeiten einfließt. Die Oberfläche dieses Farbkörpers wird durch Spektren erzeugt, die dem unten gezeigten Rechteckspektrum entsprechen. Die Oberfläche stellt die Gesamtheit aller Optimalfarben (Farben höchster Sättigung und Leuchtkraft) dar. Das Volumen des Farbkörpers bildet alle theoretisch realisierbaren Farben ab.

Rechteckspektrum einer Mittel-Optimalfarbe nach Ostwald, hier mit 40 nm Breite (550 nm bis 590 nm)

Obwohl bereits Leonardo da Vinci Versuche unternommen hatte, Farben künstlerisch zu ordnen, blieben die Versuche wegen der fehlenden theoretischen Grundlagen in Ansätzen stecken. Noch um 1800, zu Zeiten von Goethes Interesse für die Farblehre, waren die Vorstellungen zu Farben sehr subjektiv orientiert. Das Ziel war noch vorwiegend, Malern die Beziehungen zwischen Farben zu erleichtern. Beispielhaft sei Runges Farbkugel[2] genannt.

Um 1900 erforderte die fortschreitende Industrialisierung numerische Farbangaben, auch ohne momentan vorhandene Farbvorlage soll die Festlegung eines Designs möglich werden. Diesem Ziel Ordnung in die Vielfalt der Farbnuancen zu bringen dienten die Arbeiten von Munsell, Ostwald, Rösch, Schrödinger voraus. Wichtige physikalische Grundlagen stammen von Maxwell, Young, Hering. Messungen zum Farbreiz wurden 1928 von William David Wright und Guild ausgeführt.[3]

Im Ergebnis dieser Arbeiten war die erste Normung eines Farbraumes durch die Internationale Beleuchtungskommission (CIE) möglich geworden. Ausarbeitungen der CIE sind Empfehlungen, die weltweit durch die speziellen Gremien der Geräteklassen Abstimmung ermöglichen.

Das erste Farbmodell wurde 1931 von der CIE mit dem Tristimulus-Modell vorgeschlagen. Dieses Modell beruhte auf dem gemittelten 2°-Normalbeobachter (aus einer Gruppe von 17 Versuchspersonen). Dieses 2°-Gesichtsfeld entspricht der Größe der Netzhautregion mit der dichtesten Packung von Zapfen (Farbrezeptoren) im menschlichen Auge, der Sehgrube (Fovea). Da die Probenflächen zur Abmusterung allerdings größer waren, wurde 1964 das Tristimulus-Modell für den 10°-Normalbeobachter eingeführt. Da die heutigen Dimensionen für farbige Kleinbildschirme, zum Beispiel für MP3-Player, portable Spielekonsolen und Handys sehr gering ausfallen, gewinnt der 2°-Normalbeobachter von 1931 für kleine Betrachtungswinkel wieder an Bedeutung. Bereits in den 1940er Jahren stellte MacAdam ein Problem in der xy-Fläche fest: die perzeptive Ungleichmäßigkeit im XYZ-Modell (auch als (Schuh)sohle bezeichnet), führte dazu, dass die xy-Fläche durch die Transformation ins UCS-System (Uniform Chromaticity Scale, Yuv und Yu'v') so verformt wurde, dass die Farbabstände dem Ideal der perzeptiven Gleichförmigkeit (Gleichheit von Farbabstanden im Farbraum und empfundenen Farbabstanden) stark angenähert wurden. In der ursprünglichen xy-Ebene schwankt die Größe der Toleranzellipsen in Etwa um den Faktor 20, mit den kleinsten Ellipsen im blauen Bereich und den größten Ellipsen im grünen Bereich des Diagramms. Im UCS-System von 1976 wurde diese Ungleichförmigkeit stark vermindert. Die Größe der Toleranzellipsen im CIE 1976 UCS-Diagramm (u'v'-Diargramm), schwankt ungefähr nur noch um einen Faktor 4.[4] Dies ist laut MacAdam der beste Wert, der durch Transformationen dieser Art erreicht werden kann.[5]

Die Farbarten-Fläche eliminiert die dritte Achse des Hellbezugswertes A, der mit dem Tristimuluswert Y gleichgesetzt ist. Der Hellbezugswert wird auch mit L (Luminance) bezeichnet.

1976 wurden dann von der CIE sowohl das L*a*b*- als auch das L*u*v*-Modell verabschiedet. In beiden Systemen wird die Angleichung der Farbabstände im Farbraum an die Wahrnehmung erreicht, indem beide Systeme für L* einen Term verwenden, der die dritte Wurzel des Quotienten aus dem Tristimuluswert Y und dem Weißpunkt Y_n beinhaltet. Dieser Term dient dazu, die logarithmische Helligkeitswahrnehmung des menschlichen Sehapparates nachzuahmen. Diese Nichtlinearität fließt zusätzlich in die Werte a* und b* bzw. u* und v* ein. Die nichtlineare Transformation ist umkehrbar. Das L*a*b*-Modell gilt bevorzugt für Körperfarben und kann statt in kartesischen Koordinaten auch in Polarkoordinaten (genauer Zylinderkoordinaten), in Gestalt des L*C*h°-Systems, dargestellt werden. Die zylindrische Darstellungsform ergibt die zusätzlichen Koordinaten C* (chroma) und den Farbtonwinkel h° (hue). Für Lichtfarben ist das L*u*v*-System besser geeignet, da dieses ein zugeordnetes Farbartendiagramm besitzt. L*u*v* kann ebenfalls in Zylinderkoordinaten überführt werden, mit den zusätzlichen Parametern C* (chroma), h_uv (hue). Ein dritter Parameter, s_uv (psychometric saturation), kann, im Gegensatz zum L*C*h°-System, ebenfalls abgeleitet werden.

Die Entwicklung und Normierung der fotografischen und elektronischen Geräte brachte eine Anzahl von speziell ausgewählten RGB-Farbräumen (sRGB, Adobe RGB 1998), die an die eingesetzten Leuchtstoffe (Phosphore) für Rot, Grün und Blau und an realisierbare Filter (TFT-Bildschirme) angepasst wurden. Das Ziel ist es, den damit darstellbaren Farbreizen gerecht zu werden. In Darstellungen auf dem Chromazitätsdiagramm (xy-Fläche der CIE) sind RGB-Systeme Farbflächen innerhalb der durch die Phosphore (stoffliche Realisierungen der durch Elektronen angeregten Strahlung im erforderlichen Spektralbereich). Da die xy-Fläche (Schuhsohle, Hufeisen en: horseshoe) definitionsgemäß die maximal wahrnehmbaren Farben festlegt, müssen die RGB-Farbarten innerhalb des Spektralfarbenzuges liegen.

Mit dem Fortschritt der mathematischen Topologie, andererseits den steigenden Anforderungen der Reproduzierbarkeit des Farbeindruckes in der elektronischen Aufnahme- und Wiedergabetechnik werden weitere Anpassungen an die Realität notwendig sein. Anschaulich wird dieser Trend an den Farbabstandsformeln (ΔE), die das Maß im Farbraum festlegen und 1976, 1994 und 2000 modifiziert wurden.[6] Einen ähnlichen Trend stellen die ICC-Profile dar, mit diesen werden anwendungsorientierte, auch geräteorientierte Arbeitsfarbräume gebildet. Im Colormanagement ist es möglich für die Anpassung der Farbwiedergabe/-umsetzung mit unterschiedlichen Gerätekategorien die speziellen Farbräume der Geräte zu bestimmen. Durch Matrizenrechnung oder LUT (Look-Up-Tabellen) wird der Farbort aus dem speziellen Arbeitsraum des Ausgangsgerätes in einen geeigneten (möglichst) umfassenden Farbraum als Zwischenergebnis transformiert, um aus diesem „Zwischenraum“ (Vermittlungsfarbraum) wiederum den Farbort im Arbeitsfarbraum des Zielgerätes zu bestimmen.

Entwicklungen

30 bis 40 Farbmodelle wurden bislang erstellt, die sich durch den beabsichtigten Einsatzbereich unterscheiden. Entsprechend lassen sie sich kategorisieren in:

Technisch-physikalische Modelle, die den Farbreiz aus realen oder idealisierten farbgebenden Stoffen erzeugen, wie
- RGB,
- CMY,
- CMYK.
Wahrnehmungsorientierte Modelle, die Farben durch die Merkmale Helligkeit, Sättigung und Farbton beschreiben, wie
- HSV,
- HSL,
- HSB und HSI.
Spezielle Modelle für die Farbdarstellung von selbstleuchtenden Geräten, wie
- Röhrenmonitor, Farbfernsehbildröhre
- Flüssigkristallbildschirme
- Plasmabildschirme
- PAL-TV
- NTSC-TV

Farbabstandsformeln

Farbabstände können mit Farbabstandsformeln quantitativ bestimmt werden. Das Ergebnis solch einer Formel, ΔE, gilt als recht zuverlässiger Indikator für wahrgenommene Farbabstände. Die seit Einführung des Lab-Farbraums 1976 geänderte Farbabstandsformel ΔE 1976 und die Entwicklung ihrer Nachfolger verdeutlicht, dass es sich dabei keineswegs um ein triviales Problem handelt. ΔE 1976 wurde aus dem euklidischen Abstandsmaß zwischen den Farbörtern ermittelt. Diese einfache Berechnung wurde erheblich weiterentwickelt und erweitert zu CIE94 (ΔE 1994), und 1995 veröffentlicht. CIE94 wurde im Jahr 2000 nochmals erweitert zu CIEDE2000 (ΔE 2000). CIEDE2000 ist streng genommen ein Hybridmodell, da nicht nur die Farbabstandsformeln geändert wurden, sondern auch eine einfache Transformation des LAB-Farbraumes der eigentlichen Farbabstandsberechnung vorausgeht. Der Weg der Farbraumanpassung wurde im DIN99-Farbraum vollständig umgesetzt. Die Farbabstandsformel $\Delta \mathrm {E} _{99}$ bleibt unberührt und ist im Aufbau mit dem ursprünglichen ΔE 1976 identisch. Eine weitere gebräuchliche Farbabstandsformel ist ΔE CMC(l:c), entwickelt vom Colour Measurement Committee of the Society of Dyers and Colourists of Great Britain (Farbmessungskomitee der Gesellschaft der Färber und Koloristen Großbritanniens), die 1984 veröffentlicht wurde.

Bei der Weiterentwicklung wurden auch früh zweckgebundene Faktoren eingeführt. Besonders für die Textilindustrie (ΔE CMC(l:c)) wurden spezielle Korrekturfaktoren in die Berechnungen des Farbabstandes eingeführt. Diese Faktoren können auch für die Farbabstandsbestimmung bei grafischen Anwendungen angepasst werden.

Variation der Farbräume

Eine Sonderstellung nimmt der DIN99-Farbraum ein. Er wurde erstmals 1999 als Farbraum nach DIN 6176 veröffentlicht und später zur DIN 6176:2001-03 weiterentwickelt. Anstelle einer Anpassung der Farbabstandsformeln wurde eine komplette Transformation des CIELAB-Farbraumes vorgenommen. Damit lassen sich Farbabstände als euklidische Abstände nach dem gleichen Prinzip wie ΔE des CIELAB-Farbraums bestimmen.

Wirtschaftliche Bedeutung des Farbabstandes

Der Farbabstand ist für Vertragsgestaltungen (Welche Farbe muss „Ferrari-roter“ Autolack haben?) und auch für die Farbrezeptierung von Interesse. Besonders bei Farben mit hohem Wiedererkennungswert, wie bei vielen Marken als Corporate Identity üblich, ist eine durchgängig einwandfreie Farb(re)produktion und -wiedergabe sehr wichtig. Im Bereich des Verkehrswesens sind Farben für Lichtsignale wie Ampeln genau vorgeschrieben. Sie müssen dementsprechend farbgenau vom Hersteller geliefert werden. Bei „weiß-grauen“ (nahezu unbunten) Farben besteht zusätzlich das Problem, dass selbst kleinste Abweichungen zu deutlich wahrnehmbaren Farbstichen (Farben von Hose und Jackett „beißen“ sich) führen können, was in vielen Bereichen, etwa beim Nachkauf von Wandfarben, bei Schnittteilen von Kleidung oder bei Autolacken nicht akzeptabel ist. Wirtschaftlich entstehen schwerwiegende Konsequenzen für den Hersteller oder Lieferanten.

Farbmuster und Farbkatalog

Farbenkatalog

Die Darstellung von Farbräumen wird oft durch abstrakte topografische Beschreibungen realisiert. Eine Alternative dazu bilden Farbmuster in einem Farbenkatalog. Allerdings werden technisch bedingt nur ausgewählte Farben präsentiert. Für alle Farben eines Farbraumes, also den kontinuierlichen Übergang aller Farbörter ist dies für Lichtarten denkbar, aber praktisch nicht möglich.

Varianten der Farbraumgestalt

Ein Farbraum beschreibt die Farben, die von einem Eingabegerät (Sehsinn, Fotoapparat, Scanner) oder einem Ausgabegerät (Bildschirm, Ausbelichter, Drucker, Projektor) unter spezifischen Bedingungen erkannt respektive dargestellt werden können. Wie jeder Mensch individuell Farben wahrnimmt, haben auch Geräte, zumindest Geräteklassen, unterschiedliche Farbräume, in denen sie Farben registrieren oder darstellen. Eine solche Individualität ist durch Produktionsschwankungen und Konstruktionsunterschiede bedingt.

Weitere Abweichungen entstehen durch optische Effekte, die bei der messtechnischen Erfassung von Farbräumen nicht berücksichtigt werden:

Eingabegeräte (Sehsinn, Fotoapparat, Scanner) verändern in starkem Maße ihre Farbsensibilität bei wesentlichen Helligkeitsunterschieden. Da dieser Fall in der Praxis eher die Regel als die Ausnahme darstellt, kann ein unter Normbedingungen erstellter Farbraum nur eine Orientierungshilfe darstellen.
Ausgabegeräte (Bildschirm, Ausbelichter, Drucker, Projektor) arbeiten unter bestimmten Lichtverhältnissen. Je nach Farbtemperatur des Umgebungslichts werden die Farben vom Auge verschieden wahrgenommen. Nur ein Ausgabegerät, das unter Normlichtbedingungen benutzt wird, liefert Ergebnisse, die dem vorher ermittelten Farbraum nahekommen.

Ein großer Teil dieser Unterschiede wird durch automatische Bildoptimierungen korrigiert. Dabei werden metamere Effekte ausgenutzt, die – vereinfacht erklärt – Farben simulieren. Diese Farbsimulation ist technisch hochentwickelt und fester Bestandteil im Alltag. Ein typisches Beispiel sind Tintenstrahldrucker, die durch einen hohen Schwarz-Anteil die Mängel bei der Darstellung von Farben kaschieren.

Rechts ist ein Ausdruck ohne zusätzlichen Schwarzanteil zu sehen. Die Farbmängel sind deutlich zu erkennen. Der hohe Schwarzanteil des linken Bildes wird oft als angenehm empfunden, da er gleichzeitig einen hohen Schärfeeindruck simuliert.

Einige Farbräume und Farbmodelle

In vielen Anwendungsbereichen spielen spezialisierte Modelle und deren Räume eine Rolle:

LMS-Farbraum – der physiologische Farbraum, der auf den spektralen Empfindlichkeiten der L-, M-, S-Zapfen aufbaut.
XYZ-Farbraum – von der CIE ursprünglich aufgestellter Normfarbraum, auf rechnerischen Koordinaten X, Y, Z konstruiert, die aus Zapfenempfindlichkeiten erstellt sind.
RGB-Farbraum – Computermonitore, Internetstandard.
CMYK-Farbmodell – Desktoppublishing, Druck-Endstufe.
HSV-Farbraum mit den Varianten HSL, HSB, HSI – Design, Dokumentation von Malerei, Videokunst.
Lab-Farbraum – CIE-Farbenraum aus XYZ abgeleitet, der ebenfalls alle wahrnehmbaren Farben umfasst; und dessen Weiterentwicklung DIN99-Farbraum.
LCh°-Farbraum bezeichnet keinen weiteren Farbraum im eigentlichen Sinne, sondern die Darstellung von HSV, LUV oder LAB in Polarkoordinaten.
I1I2I3-Farbraum – rechentechnisch optimierter Raum der Bildverarbeitung.
YCbCr-Farbmodell (manchmal kurz YCC genannt, vgl. unten) – digitales Fernsehen, sowohl digitales PAL als auch digitales NTSC, DVB, JPEG, MPEG, DVD-Video.
xvYCC – gegenüber YCbCr erweiterter Farbraum, der die gesamten 8 Bit pro Farbkanal nutzt und für neue Flachbildschirme verwendet werden kann.
YPbPr-Farbmodell – analoges HDTV, analoges Component Video.
YUV-Farbmodell – für analoges PAL und NTSC.
YIQ-Farbmodell – veraltet, früher verwendet bei analogem NTSC.
YDbDr-Farbmodell – für analoges SECAM.
YCC-Farbmodell – Kodak Photo CD.

Farbwerte bei der Darstellung von Internetseiten

Die Angabe der Farbwerte in den Cascading Style Sheets ist ein anschauliches Beispiel für ein dreidimensionales Farbmodell.[7] Definiert sind die Werte im System eines RGB-Farbmodells mit Rot, Grün und Blau. Der Anwendungsfarbraum bei Röhrenmonitoren ist der Farbraum des Bildschirms mit den typischen Leuchtstoffen, die bei Elektronenanregung in Rot, Grün und Blau phosphoreszieren. Der zugrunde liegende Standard ist sRGB, der als Primärvalenzen die im ITU-R BT.709-5-Standard festgelegten Farbkoordinaten verwendet.

CSS eines Paares komplementärer Farben und die daraus folgende farbgebende Wirkung
`background-color:rgb(255,0,229)`
`background-color:rgb(0,255,150)`

Im „CSS(-rgb)-Modell“ werden für den Hintergrund (background) des Feldes der Website Werte zwischen 0 und 255 definiert (also in 2⁸ Werte). Im Beispiel steht

ein „Purpur“ mit folgenden Farbwerten
- r = 255 für die ideale Basisfarbe Rot in voller Reinheit und Stärke,
- g = 0 entsprechend für fehlende Basisfarbe Grün,
- b = 229 legt fest, dass die Basisfarbe Blau zu 1,055 × (229/255)^2,4 − 0,055 = 76 % anteiliger Stärke beteiligt sein soll (siehe sRGB-Farbraum)
ein „Grün“ mit folgenden Farbwerten, die (RGB-)Komplementärfarbe
- r = 0 fehlende Basisfarbe Rot,
- g = 255 Basisfarbe Grün in voller Stärke und Intensität,
- b = 150 komplementäre Basisfarbe Blau in 1,055 × (150/255)^2,4 − 0,055 = 24 % anteiliger Stärke (24 % + 76 % = 100 %)

Durch die verwendete Software des PCs werden die Farbwerte der CSS umgerechnet. Die drei Bildschirmleuchtstoffe für Rot, Grün und Blau werden in der Strahlintensität angesteuert. In ausreichendem Abstand vom Bildschirm führt dieser Farbreiz beim Nutzer zu einer Farbvalenz in seinem „individuellen Zapfenfarbraum“. So entsteht beim Betrachten der Website der angestrebte Farbeindruck. Der Zapfenfarbraum des Betrachters („Jener“ der „jetzt“ „diesen“ Bildschirm ansieht.) ist ein LMS-Farbraum des Betrachter„individuums“.

Farbsystem für Bildschirme

Beim Mischen dreier Primärfarben (RGB-System) können Farben mit herkömmlichen Darstellungsgeräten, wie Röhren- und LC-Bildschirmen, nur im Rahmen der Emissionsquellen oder durch absorbierende Färbemittel (Filter) erzeugt werden. Farbsysteme mit wellenlängengleicher Farbe und Helligkeit (HSV) sind besser dafür geeignet, die reinen Farben zu bezeichnen; die technische Interpretation ist aber schwieriger. Die Sonderstellung der Purpur-/Magentafarben wird im hufeisenförmigen CIExy- oder CIELuv-Farbdiagramm durch die abschließende Gerade, die den äußersten Blauwert mit dem äußersten Rotwert verbindet, erkennbar.

Die CIE-Systeme

Tristimulusraum von 1931 (2°-Normalbeobachter, engl.: 2° standard observer), 1964 mit neuen Datensätzen für ein Sichtfeld von 10° ergänzt (10°-Normalbeobachter, engl.: 10° supplementary standard observer)
CIE XYZ-Farbraumsystem (Chromatizitäts-Diagramm)
- Normfarbtafel
- da die Spektralwertfunktion y(λ) genau der Helligkeitsempfindlichkeit beim Zapfensehen entspricht, kann die (nicht normalisierte) Koordinate Y als Helligkeitswert (Luminanz) verwendet werden, hier sollte als Konstante besser „A“, statt Y gewählt werden
- Koordinaten: Y, x, y oder in der Normfarbtafel nur x, y
CIEYUV-Farbraumsystem, auch CIE UCS, 1960 vorgeschlagen, (CIE 1960 UCS, Uniform Chromaticity Scale, de: Einheitliche Farbskala)
- lineare Transformation von CIEXYZ, um die ortsabhängige Nichtlinearität der wahrgenommenen Farbabstände zu verringern
- nur 2D-Farbabstände definiert
- Trotz oft gleicher Schreibweise (YUV statt CIEYUV oder CIEYuv) nicht mit YUV aus der Videotechnik verwandt!
- Koordinaten: Y, u, v
YUV-Farbmodell, (CIE 1964 UCS), 1964 vorgeschlagen
- lineare Transformation des CIEYUV (Yuv)-Farbraums
- weiterer lineare Transformation, um die ortsabhängige Nichtlinearität der wahrgenommenen Farbabstände zu verringern
- nur 2D-Farbabstände definiert
- Koordinaten: Y, u', v'
CIELUV-Farbraumsystem von 1976
- nichtlineare Transformation des CIEXYZ-Farbraums, bezieht den CIE 1964 UCS-Farbraum (CIEYU'V') für den Weißpunkt ein, Transformation ist umkehrbar
- Spektrallinie ist äußere Begrenzung des Farbdiagramms, daher ist die absolute Sättigung (relativ zur Spektrallinie) einer Farbe messbar
- Farbmischungen liegen auf Geraden im Raum, daher sehr gut für farbmetrische Berechnungen und Darstellung additiver Farbmischung geeignet, wie zur Beschreibung selbstleuchtender Quellen (Lichtfarben)
- Farbdiagramm psychometrisch orientiert und orientiert sich an der Gegenfarbtheorie, ähnlich wie CIELAB
- Schwerpunkt Gleichabständigkeit der Farbwahrnehmung, vergleichbar mit dem LAB-Farbraum
- Koordinaten: L*, u*, v*
CIELAB-Farbraumsystem von 1976
- nichtlineare Transformation von CIEXYZ, Transformation ist umkehrbar
- Farbdiagramm psychometrisch orientiert und basiert auf der Gegenfarbtheorie
- im Gegensatz zu CIELUV ist in CIELAB die Messung der absoluten Sättigung (relativ zur Spektrallinie) nicht möglich, da die Spektrallinie im LAB-Farbraum keine bevorzugte Lage besitzt und im Diagramm statt der Sättigung die Buntheit einer Farbe dargestellt wird
- keine Farbtafel vorhanden
- gute Gleichabständigkeit von Farbabständen durch die nichtlineare Transformation gewährleistet
- besonders zur Beschreibung von nichtleuchtenden Farben (Körperfarben) verwendet
- Koordinaten: L*, a*, b*

Systeme außerhalb der CIE

DIN99-Farbraum, (Farbraum nach DIN 6176), seit 1999
- Koordinaten: $\mathrm {L_{99}}$ , $\mathrm {a_{99}}$ , $\mathrm {b_{99}}$
- Alternative zur Farbabstandsformel CIE94, vergleichbare Gleichabständigkeit
- Durch spätere Weiterentwicklung (DIN 6176:2001-03) Gleichabständigkeit verbessert. Die derzeit beste Variante (DIN99d) liegt qualitativ zwischen CIE94 und CIEDE2000
- Sonderstellung gegenüber allen CIELAB-Nachfolgern, statt der Farbabstandsformeln wird der gesamte Farbraum transformiert
- Anpassung von $\mathrm {L^{*}}$ , dunkle Farben stärker gewichtet, helle komprimiert
- „runde“ Gestalt (Gleichabständigkeits-Idealform) durch radiale Kompression der Bunttonebene, dadurch:
- Farbabstände nahe der Unbuntachse werden durch die radiale Kompression gesättigter Farben stärker gewichtet (ähnlich CIEDE2000)
- Berechnung einfacher als CIE94 und CIEDE2000, $\mathrm {\Delta E_{99}}$ $\text{[math]}$ wird wie $\mathrm {\Delta E}$ $\text{[math]}$ berechnet, da der Farbraum transformiert wird und die Farbabstandsformeln unberührt bleiben
  - Im Falle der Variante DIN99d findet ein Teil der Transformation schon im XYZ-Farbraum statt

Farbkomponenten

Farbkomponenten, die für die CIE Farbraumsysteme essenziell sind:

CIE XYZ oder Tristimulus-Werte

Color/Image Appearance Models (CAM/IAM)

Derzeit werden intensiv Untersuchungen und Forschungen im Bereich der „Color Appearance Models“ (CAM), zu Deutsch etwa: Modelle zur Erscheinung von Farbe, und „Image Appearance Models“ (IAM), zu Deutsch: Modelle zur Erscheinung von Bildern, betrieben. Da die mathematischen Beschreibungen, die nur Farben und Farbabstände berechnen, höhere Ebenen der menschlichen Farbwahrnehmung nicht berücksichtigen, sind fortgeschrittenere Modelle gefragt, da eine Vielzahl von anderen Faktoren starke Einflüsse auf den Gesamteindruck haben können. Die Entwicklungen von CAM und IAM entspringen der Fragestellung: „Wie erscheint eine bestimmte Farbe oder ein Bild im allgemeinen Kontext der näheren und ferneren Umgebung eines Bildes?“ Phänomene, wie etwa Simultankontrast, Adaptation an die Umgebungshelligkeit und deren zeitlichen Verlauf, Verringerung der räumlichen Auflösung beim Dämmerungs- (mesopisches Sehen) und Dunkelsehen (skotopisches Sehen) spielen nämlich eine große Rolle bei der Farbwahrnehmung.

Ein sehr alltägliches Problem in diesem Zusammenhang ist der grundlegende Widerspruch zwischen Schärfe und Schärfeempfinden. IAM sind ein Schritt in Richtung einer Lösung dieses Konflikts, da die Verarbeitung von Detailkontrasten, Farbkontrasten usw. in diesen Modellen gesondert berücksichtigt wird.

CIELAB

ist im Grunde genommen das erste CAM. Es wird schon die Adaption an den Weißpunkt berücksichtigt (Mittels Transformationsmatrizen, wie z. B. von-Kries- oder Bradford-Matrizen), außerdem die Kompression der Helligkeitswahrnehmung. Die Weiterentwicklung führte dann zu CIECAM97s.

CIECAM97s

ist genauer und umfangreicher, was die Betrachtungsbedingungen usw. angeht. Die Entwicklung wurde fortgesetzt zu CIECAM02.

CIECAM02

liefert allgemein genauere Werte für Farbabstände und berücksichtigt in größerem Umfang Bildhelligkeit, Farbhintergrund, Bildumgebung, Weißpunkt, Adaptation und Simultankontrast.

iCAM

ist ein weiterer Schritt in der Entwicklung. Der neueste Vertreter dieser Modelle ist iCAM06. Es werden lokale Farbadaptation, lokale Helligkeit und Umgebungshelligkeit, HDR, und zeitlicher Verlauf der Adaptation an die Umgebungshelligkeit berücksichtigt. Der Bereich der IAM wird betreten. iCAM06 ist im Gegensatz zu seinen Vorgängern schon ein ausgewachsenes IAM, da beispielsweise die Weißpunktadaptation und Kontrastberechnungen nicht mehr mit einem rein lokalen Modell (Pixel für Pixel), sondern räumlich berechnet werden. Somit können Bildbereiche je nach Struktur und Bildkomposition auch fernere Bereiche beeinflussen und somit den Gesamteindruck eines Bildes ändern.

Siehe auch

Farbtiefe

Weblinks

Commons: Farbräume – Sammlung von Bildern, Videos und Audiodateien

Einzelnachweise

hs-aalen.de: Was ist eigentlich Farbe? Teil 1: Farbmetrik, S. 44–49, hier S. 46.
Farbkugel nach Runge
William David Wright, Guild
R.W.G. Hunt: Measuring Colour, Kap. 3.6 – Uniform Chromaticity Diagrams
MacAdam:Color Measurement 2. ed. Springer-Verlag, Kap. 8.3 – Nonlinear Transformations of the Chromaticity Diagram
http://www.brucelindbloom.com/ Navigation: Math
CSS bei W3C

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] s-aalen.de: Was ist eigentlich Farbe? Teil 1: Farbmetrik, S. 44–49, hier S. 46.

[2] Farbkugel nach Runge

[3] William David Wright, Guild

[4] R.W.G. Hunt: Measuring Colour, Kap. 3.6 – Uniform Chromaticity Diagrams

[5] MacAdam:Color Measurement 2. ed. Springer-Verlag, Kap. 8.3 – Nonlinear Transformations of the Chromaticity Diagram

[6] ttp://www.brucelindbloom.com/ Navigation: Math

[7] CSS bei W3C