Scanline-Algorithmus
Als Scanline-Algorithmus bzw. Bildzeilenalgorithmus wird in der Computergrafik ein Bildzeile für Bildzeile (englisch scan line) arbeitendes Verfahren zur Verdeckungsberechnung von aus Polygonen aufgebauten 3D-Szenen bezeichnet. Der gesamte Darstellungsprozess wird auch Scanline-Rendering bzw. Bildzeilenrenderung genannt. Scanline-Algorithmen nutzen die Tatsache aus, dass durch die Zeile für Zeile erfolgende Arbeitsweise das Problem der Verdeckungsberechnung von drei auf zwei Dimensionen reduziert wird. Die ersten Scanline-Algorithmen wurden Ende der 1960er Jahre veröffentlicht.[1][2][3][4]
Grundprinzip
Scanline-Algorithmen basieren auf dem Kantenlisten-Algorithmus mit aktiver Kantenliste zum Füllen von Polygonen (siehe Rastern von Polygonen), der manchmal ebenfalls Scanline-Algorithmus genannt wird. Dieser Algorithmus wird dahingehend erweitert, dass er auch mehrere Polygone auf einmal rastern kann und in Zweifelsfällen entscheidet, welches Polygon vom Betrachter aus sichtbar ist.
Der Scanline-Algorithmus zum Rendern von Polygonen verwendet eine Kantentabelle, die einen Eintrag für jede Kante eines Polygons enthält. Horizontale Kanten werden ignoriert. Jeder Eintrag der Kantentabelle enthält folgende Informationen:
- die x-Koordinate des Kanteneckpunkts mit kleinerer y-Koordinate,
- die y-Koordinate des anderen Kanteneckpunkts,
- Δx, die Differenz der x-Koordinaten der Schnittpunkte mit zwei aufeinanderfolgenden Bildzeilen (der Kehrwert der Steigung der Kante),
- die Nummer des Polygons, zu dem die Kante gehört.
Zusätzlich ist eine Polygontabelle erforderlich, die für jedes Polygon, zusätzlich zu dessen Nummer, zumindest folgende Informationen enthält:
- die Koeffizienten der Ebenengleichung der Ebene, die das Polygon enthält,
- Shading- oder Farbinformationen,
- ein Flag, das während des Scanline-Algorithmus verwendet wird und angibt, ob man sich aktuell innerhalb dieses Polygons befindet. Es muss zu Beginn auf falsch initialisiert sein.
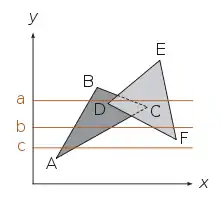
Weiterhin ist wie beim einfachen Algorithmus zum Füllen von Polygonen eine aktive Kantentabelle (Tabelle der aktiven Kanten) erforderlich, die alle Kanten enthält, die die aktuell verarbeitete Bildzeile schneiden. Für die im Beispiel angegebenen Bildzeilen enthält die aktive Kantentabelle folgende Werte:
| Bildzeile | Kanten |
|---|---|
| c | AB AC |
| b | AB AC FD FE |
| a | AB DE CB FE |
Die Bildzeilen werden von links nach rechts abgearbeitet. Bei der Bildzeile c verfährt der Algorithmus folgendermaßen: Sobald die Kante AB erreicht wird, wird das In-out-Flag des entsprechenden Polygons gesetzt; der Algorithmus ist jetzt „in“ diesem Polygon, und Pixel werden entsprechend der mit dem Polygon verknüpften Shading-Informationen eingefärbt. Sobald die Kante AC erreicht ist, wird das Flag wieder auf falsch gesetzt. Da die Kante AC die letzte in der aktiven Kantentabelle ist, ist der Vorgang für diese Bildzeile beendet. Bei der Bildzeile b sind zwei Polygone beteiligt, da sie aber hier einander nicht überlappen, betrachtet der Algorithmus genau wie im vorherigen Fall stets nur maximal ein Polygon pro Pixel.
Bei der Bildzeile a ist mehr Aufwand erforderlich. Sobald das Dreieck ABC erreicht wird, setzt der Algorithmus das entsprechende Flag in der Polygontabelle. Die Shading-Informationen dieses Polygons werden verwendet, bis die Kante DE erreicht wird. Hier wird nun auch das Flag für das Dreieck DEF gesetzt, der Algorithmus ist jetzt also „in“ zwei Polygonen gleichzeitig. Es muss nun entschieden werden, welches dieser beiden Polygone dem Betrachter näher liegt. Dies geschieht, indem mit Hilfe der gespeicherten Ebenengleichungs-Koeffizienten die z-Koordinate des Polygons an diesem Punkt berechnet wird. In diesem Beispiel hat ABC die größere z-Koordinate, also ist es nicht sichtbar. Wenn man annimmt, dass die beiden Polygone einander nicht schneiden, so werden demzufolge die Shading-Parameter des Dreiecks DEF verwendet. Wenn die nächste Kante CB erreicht ist, wird das Flag des Polygons ABC auf falsch gesetzt und der Algorithmus befindet sich nur noch im Polygon DEF, dessen Shading-Parameter weiterhin verwendet werden.
Varianten
Der grundlegende Scanline-Algorithmus berechnet die Tiefe der überlappenden Polygone an jedem Pixel. Die Anzahl dieser Berechnungen kann durch das Einteilen der Bildzeile in einzelne Bereiche („Spans“), für die jeweils nur eine Berechnung durchgeführt wird, reduziert werden. Derartige Verfahren, zu denen auch der von Watkins 1970 veröffentlichte Algorithmus gehört, werden Spanning-Scanline-Algorithmen genannt.
Scanline-Algorithmen können auch mit dem Z-Buffer kombiniert werden. Dabei wird ein nur eine Bildzeile umfassender Z-Buffer, ein sogenannter Scanline-Z-Buffer, für die aktuelle Bildzeile verwendet.[5] Er bietet sich an, wenn nicht ausreichend Speicher für einen vollständigen Z-Buffer vorhanden ist.
Vergleich mit dem Z-Buffer
Gegenüber dem Z-Buffer haben Spanning-Scanline-Algorithmen den Vorteil, dass Shading-Berechnungen nur einmal pro Pixel durchgeführt werden müssen. Allerdings beginnen und enden Spans nicht unbedingt an den Schnittpunkten mit den Kanten des sichtbaren Polygons. Dies erschwert die inkrementelle (schrittweise) Shading-Berechnung, da die Startwerte an einem beliebigen Punkt des Polygons berechnet werden müssen. Der Z-Buffer ist ab einer bestimmten Anzahl von Polygonen effizienter als Spanning-Scanline-Algorithmen, weshalb er für die heute üblichen komplexen Szenen meist vorgezogen wird.[6]
Literatur
- Hans-Joachim Bungartz u. a.: Einführung in die Computergraphik: Grundlagen, geometrische Modellierung, Algorithmen. Vieweg, Braunschweig 2002, ISBN 3-528-16769-6
- James Foley u. a.: Computer Graphics: Principles and Practice. Addison-Wesley, Reading 1995, ISBN 0-201-84840-6
- William Newman, Robert Sproull: Principles of Interactive Computer Graphics, S. 313–321. McGraw-Hill, New York 1973, ISBN 0-07-046337-9
- David Rogers: Procedural Elements for Computer Graphics. WCB/McGraw-Hill, Boston 1998, ISBN 0-07-053548-5
Einzelnachweise
- Jack Bouknight: A procedure for generation of three-dimensional half-toned computer graphics presentations. Communications of the ACM 13, 9 (Sep. 1970): 527–536, ISSN 0001-0782
- Jack Bouknight, K. Kelley: An algorithm for producing half-tone computer graphics presentations with shadows and movable light sources. In AFIPS Conference Proceedings, vol. 36: 1970 Fall Joint Computer Conference. S. 1–10. AFIPS Press, Montvale 1970
- Gary Scott Watkins: A Real Time Visible Surface Algorithm. Dissertation, University of Utah 1970
- C. Wylie u. a.: Halftone perspective drawings by computer. In AFIPS Conference Proceedings, vol. 31: 1967 Fall Joint Computer Conference. S. 49–58. AFIPS Press, Montvale 1967
- A. J. Myers: An Efficient Visible Surface Program. Report to the National Science Foundation, Computer Graphics Research Group, Ohio State University 1975
- Alan Watt: 3D Computer Graphics, S. 194. Addison-Wesley, Harlow 2000, ISBN 0-201-39855-9