Diffusions-Tensor-Bildgebung

Die Diffusionsgewichtete Magnetresonanztomografie (abgekürzt DW-MRI von englisch diffusion-weighted magnetic resonance imaging) ist ein bildgebendes Verfahren, das mit Hilfe der Magnetresonanztomografie (MRT) die Diffusionsbewegung von Wassermolekülen in Körpergewebe misst und räumlich aufgelöst darstellt. Sie wird zur Untersuchung des Gehirns eingesetzt, da sich das Diffusionsverhalten im Gewebe bei einigen Erkrankungen des zentralen Nervensystems charakteristisch verändert und die Richtungsabhängigkeit der Diffusion Rückschlüsse auf den Verlauf der großen Nervenfaserbündel erlaubt. Wie die klassische MRT ist die diffusionsgewichtete Bildgebung nichtinvasiv: Da der Bildkontrast allein mittels magnetischer Feldgradienten erzielt wird, erfordert sie weder eine Injektion von Kontrastmitteln, noch den Einsatz von ionisierender Strahlung.

Die Diffusions-Tensor-Bildgebung (abgekürzt DTI von englisch diffusion tensor imaging oder DT-MRI von diffusion tensor magnetic resonance imaging) ist eine häufig eingesetzte Variante der DW-MRI, die auch die Richtungsabhängigkeit der Diffusion erfasst. Pro Volumenelement (Voxel) bestimmt sie nicht nur einen einzelnen Zahlenwert, der im Schnittbild als Grauwert dargestellt werden kann, sondern berechnet einen Tensor (konkret: eine 3×3-Matrix), der das dreidimensionale Diffusionsverhalten beschreibt. Derartige Messungen sind zeitaufwändiger als herkömmliche MRT-Aufnahmen und erzeugen größere Datenmengen, die der Radiologe erst durch den Einsatz verschiedener Visualisierungs-Techniken interpretieren kann.

Die Diffusions-Bildgebung entstand in den 1980er Jahren. Inzwischen wird sie von allen neuen MRT-Geräten unterstützt und hat sich im klinischen Alltag zur Schlaganfall-Diagnose etabliert, da die betroffenen Hirnregionen in diffusionsgewichteten Bildern früher zu erkennen sind als in der klassischen MRT. Die Diffusions-Tensor-Bildgebung wurde Mitte der 1990er Jahre von Peter J. Basser und Denis Le Bihan entwickelt. Einige Kliniken setzen sie zur Operations- und Bestrahlungs-Planung ein. Darüber hinaus wird die DT-MRI in der medizinischen Forschung zur Erforschung von Krankheiten, die mit Veränderungen der weißen Substanz einhergehen (wie etwa Morbus Alzheimer oder Multiple Sklerose) genutzt. Auch die Weiterentwicklung der diffusionsgewichteten Bildgebung selbst ist aktueller Forschungsgegenstand, etwa im Rahmen des Human Connectome Project.

Die DT-MRI ermöglicht eine Rekonstruktion von Nervenbahnen im Gehirn (Traktografie).

Messverfahren

Grundlagen

Die Diffusions-Bildgebung beruht auf den gleichen physikalischen Grundlagen wie herkömmliche MRT (siehe auch Hauptartikel Magnetresonanztomografie). Sie nutzt die Tatsache, dass Protonen ein magnetisches Moment besitzen und sich in einem äußeren Magnetfeld entweder parallel (niederenergetischer Zustand) oder antiparallel (hochenergetischer Zustand) ausrichten. Im Gleichgewicht befindet sich eine größere Anzahl der Protonen im niederenergetischen Zustand, wodurch ein Summenvektor parallel zum äußeren Feld entsteht (paramagnetischer Effekt). Die Richtung des äußeren Felds bezeichnet man im Kontext der MRT als z-Achse; senkrecht dazu steht die xy-Ebene.

Die Rotationsachse der Protonen präzediert um die z-Achse. Die Frequenz dieser Bewegung ist zur Feldstärke des äußeren Magnetfelds proportional und wird Larmorfrequenz genannt. Eine hochfrequente elektromagnetische Welle („HF-Puls“) mit dieser Frequenz regt die magnetischen Momente zu einem Wechsel ihres Zustands an (Kernspinresonanz). Dadurch ändert sich in Abhängigkeit von Stärke und Dauer des Pulses die Ausrichtung des Summenvektors, er „klappt um“. Die umgeklappten Momente rotieren zunächst phasengleich, so dass der Summenvektor nun auch eine (rotierende) Komponente in der xy-Ebene besitzt.

Dieser Effekt kann mit einer Mess-Spule beobachtet werden, die senkrecht auf der xy-Ebene steht; in ihr induziert das rotierende Netto-Moment eine Spannung. Schaltet man den HF-Puls ab, kehren die Protonen wieder in ihren Gleichgewichtszustand zurück. Durch Inhomogenitäten im äußeren Feld und thermische Stöße („Spin-Spin-Wechselwirkung“) verliert sich auch die Phasenkohärenz und die xy-Komponente des Summenvektors verschwindet. Zur Beobachtung der Diffusionsbewegung muss man ein „ortsaufgelöstes“ NMR-Experiment machen, also ein Feldgradienten-NMR-Experiment, in dem durch das Anlegen von Magnetfeld-Gradienten die NMR-Signalfrequenz ortsabhängig gemacht wird und somit Ortsveränderungen der Wassermoleküle durch Diffusion beobachtbar werden.

Diffusionsgewichtete MRT-Sequenzen

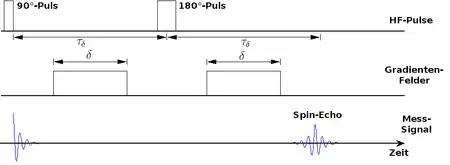
Schema der Stejskal-Tanner-Sequenz. Eine Diffusionsbewegung entlang der Gradientenfelder wird als Abschwächung des Spin-Echos gemessen (Erläuterungen im Artikeltext).

Eine diffusionsgewichtete MRT-Sequenz (siehe Schema) beginnt damit, dass der Summenvektor zunächst um 90° in die xy-Ebene gekippt wird. Die Diffusionswichtung geschieht durch ein kurzzeitig geschaltetes Gradientenfeld, das die Feldstärke des äußeren Magnetfelds in einer vorgegebenen Richtung variiert. Entlang dieser Richtung präzedieren die Kerne nicht mehr mit der gleichen Larmorfrequenz; sie geraten aus der Phase und die in der Mess-Spule induzierte Spannung verschwindet.

Anschließend kehrt man mit einem erneuten HF-Puls die Drehrichtung der Kerne um (180°-Puls) und schaltet nochmals das gleiche Gradientenfeld ein. Aufgrund der identischen Frequenzunterschiede bei umgekehrter Drehrichtung gelangen die magnetischen Momente nun wieder in Phase und es tritt erneut eine Spannung auf, das Spin-Echo. Dies ist allerdings schwächer als das Signal zu Beginn der Sequenz, da ein Teil der Kerne nicht wieder in Phase gerät – das sind insbesondere diejenigen, die sich während der Messung in Richtung des Gradientenfelds bewegt haben. Eine Diffusionsbewegung in dieser Richtung äußert sich also in einer Abschwächung des Signals.

Wie oben beschrieben schwächen auch Spin-Spin-Wechselwirkungen das Spin-Echo ab; die Auswirkungen von Feldinhomogenitäten werden dagegen durch die Mess-Sequenz eliminiert. Um den Einfluss der Diffusionsbewegung abschätzen zu können, ist daher zum Vergleich eine zweite Aufnahme notwendig, in der kein Gradient geschaltet wird.

Das physikalische Modell

Um die Richtungsabhängigkeit der Diffusion zu beschreiben, nutzt die DT-MRI das mathematische Modell der freien Diffusion, die in der Physik durch die Fickschen Gesetze beschrieben wird. Im dreidimensionalen Fall lautet das erste Ficksche Gesetz

{\vec {J}}=-D\nabla c.

Es stellt die Teilchenstromdichte ${\vec {J}}$ in Beziehung zum Konzentrationsgradienten $\nabla c$ . Als Proportionalitätsfaktor tritt dabei der skalare Diffusionskoeffizient $D$ auf. In anisotropen Medien ist der Diffusionskoeffizient richtungsabhängig und muss in obiger Gleichung daher durch den Diffusions-Tensor $\mathbf {D}$ ersetzt werden – eine symmetrische 3×3-Matrix, die hier eine lineare Abbildung beschreibt.

Die Diffusions-Bildgebung misst die Selbstdiffusion von Wasser, das heißt die Brownsche Molekularbewegung, die Wasser-Moleküle aufgrund ihrer thermischen Energie ständig ausführen. Diese ist nicht mit einem Konzentrationsgradienten verbunden, bildet jedoch die physikalische Grundlage des durch die Fickschen Gesetze beschriebenen Prozesses und folgt daher dem gleichen mathematischen Modell. Dennoch ist das beschriebene Diffusionstensor-Modell streng genommen in der DT-MRI nicht anwendbar, weil hier keine freie Diffusion vorliegt, sondern die Molekularbewegung durch Hindernisse auf zellularer Ebene eingeschränkt ist. Ziel des Verfahrens ist es, aus der Beobachtung dieser Einschränkung Rückschlüsse auf die Struktur des Gewebes zu ziehen, in dem das Wasser diffundiert.

Aus diesem Grund spricht man statt von Diffusionskoeffizienten genauer von einem apparent diffusion coefficient (ADC), einem „scheinbaren“ Diffusionskoeffizienten, der nicht nur von der Richtung, sondern auch von der Diffusionslänge abhängt: Schaltet man die Gradientenfelder in so kurzem zeitlichen Abstand, dass der Großteil der Moleküle während dieser Zeit auf kein Hindernis trifft, erscheint die Diffusion frei; erhöht man die Diffusionszeit, zeigt sich die Einschränkung der Bewegung, der ADC nimmt ab. In technischen Anwendungen nutzt man diesen Effekt, um durch Messungen mit variabler Diffusionszeit den Porendurchmesser von mikroporösen Stoffen zu ermitteln. In der Diffusions-Tensor-Bildgebung ist die Größenordnung der untersuchten Zellstrukturen bekannt, so dass die Diffusionszeit an sie angepasst werden kann. In der Praxis der DT-MRI kann man daher die Abhängigkeit des ADC von der Diffusionslänge ignorieren und spricht häufig weiterhin vereinfachend von Diffusionskoeffizienten.

Berechnung des Diffusions-Tensors

Die zentrale Gleichung der Diffusions-Tensor-Bildgebung beschreibt die Abschwächung des Mess-Signals in Abhängigkeit von den Messparametern und dem Diffusions-Tensor. Sie wird als Stejskal-Tanner-Gleichung bezeichnet:

A({\vec {g}})=A_{0}\cdot e^{-b\,{\vec {g}}^{T}\mathbf {D} {\vec {g}}}.

$A({\vec {g}})$ steht hier für die Signalstärke unter Wirkung eines Gradientenfelds in Richtung ${\vec {g}}$ , $A_{0}$ ist die Signalstärke einer ungewichteten Messung und $b$ fasst die Messparameter zusammen. Der Diffusions-Tensor $\mathbf {D}$ beschreibt eine positiv semidefinite quadratische Form, die jeder Richtung ${\vec {g}}$ einen ADC zuordnet.

${\vec {g}}$ und $b$ werden vor der Messung festgelegt. $A({\vec {g}})$ und $A_{0}$ sind nach der Messung bekannt. Da die symmetrische Matrix $\mathbf {D}$ sechs Freiheitsgrade besitzt, sind neben der ungewichteten mindestens sechs diffusionsgewichtete Messungen in verschiedenen Richtungen notwendig, um mittels der Gleichung den vollständigen Diffusionstensor schätzen zu können. Da die Genauigkeit der Ergebnisse aufgrund von Rauschen und Mess-Artefakten eingeschränkt ist, werden die Messungen in der Regel wiederholt oder zusätzliche Richtungen herangezogen. Die Schätzung des Tensors erfolgt dann beispielsweise nach der Methode der kleinsten Quadrate.

Die hohe Zahl von Einzelmessungen erklärt den Zeitaufwand des Verfahrens, der je nach Anzahl der Schnittbilder, benötigter Genauigkeit und Feldstärke des Scanners zwischen einigen Minuten und einer Stunde beträgt. Da das Verfahren empfindlich auf äußere Bewegungen reagiert, wird der Kopf des Probanden während dieser Zeit durch ein Gestell fixiert.

Interpretation des Diffusionskoeffizienten

Im Hirngewebe ist die Beweglichkeit der Wasser-Moleküle durch Hindernisse wie zum Beispiel Zellmembranen eingeschränkt. Insbesondere können sich die Moleküle in Anwesenheit dicht gepackter Nervenfasern entlang der langgestreckten Axone ungehinderter bewegen als quer zu ihnen. Die grundlegende Annahme bei der Interpretation von Diffusions-Tensor-Daten ist daher, dass die Richtung des größten Diffusionskoeffizienten den Verlauf der Nervenfasern widerspiegelt.

Eine solche Interpretation muss berücksichtigen, dass die Axone mit einem Durchmesser im Mikrometer-Bereich deutlich unterhalb der Auflösung des Verfahrens liegen, die wenige Millimeter beträgt. Das gemessene Signal stellt also einen Mittelwert über ein bestimmtes Volumen dar, der nur dann aussagekräftig ist, wenn das Gewebe innerhalb dieses Gebiets homogen ist. Daher können nur größere Nervenfaserbündel dargestellt werden. Die genauen Mechanismen, die dem beobachteten Diffusionsverhalten zugrunde liegen, sind nicht abschließend geklärt. Aufgrund der bisherigen Untersuchungen geht man davon aus, dass die Richtungsabhängigkeit sowohl die Moleküle innerhalb als auch jene außerhalb der Zellen betrifft und durch die Myelinisierung von Nervenfasern verstärkt, aber nicht allein verursacht wird.[1]

Auch in Muskelfasern weist die Diffusionsbewegung eine klare Vorzugsrichtung auf. So wurde das Diffusions-Tensor-Modell zuerst mittels Messungen an Skelettmuskeln erprobt, da die Ergebnisse hier leicht zu verifizieren sind.[2] Auch der Aufbau des Herzmuskels von Säugetieren, in dem die Ausrichtung der einzelnen Fasern zwischen innerer und äußerer Wand (Endokard bzw. Epikard) um etwa 140° rotiert, konnte mittels Diffusions-Tensor-Messungen an präparierten Herzen sichtbar gemacht werden. Mit speziell angepassten Mess-Sequenzen ist auch eine Untersuchung des schlagenden Herzens möglich; diese ist jedoch aufwändig und bisher (Stand: 2012) noch keine klinische Routine.[3]

Visualisierung

In DTI-Schnittbildern wird die Hauptrichtung der Diffusion häufig durch Farben dargestellt.

Diffusions-Ellipsoide erlauben es, Ausschnitte der Daten detailliert darzustellen.

Ein vollständiger Diffusions-Tensor-Datensatz enthält mehr Informationen, als der Mensch durch eine einzige Abbildung aufnehmen könnte. Daher wurde eine Vielzahl von Techniken entwickelt, die sich jeweils darauf beschränken, bestimmte Aspekte der Daten zu veranschaulichen und sich gegenseitig ergänzen. In der Praxis etabliert haben sich Darstellungen von Schnittbildern, Traktografie, sowie Tensor-Glyphen.

Schnittbilder

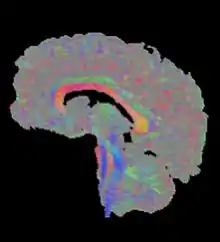
Zur Darstellung von Schnittbildern, wie sie aus der traditionellen MRT bekannt sind, werden die Diffusions-Tensoren auf einen Grau- oder Farbwert reduziert. Grauwerte werden aus den Eigenwerten des Diffusions-Tensors berechnet. Üblich sind vor allem der mittlere Diffusionskoeffizient und die Fraktionale Anisotropie. Letztere gibt an, wie richtungsabhängig die Diffusion ist und gilt als Indikator für die Unversehrtheit eines Faserbündels. Derartige Bilder werden zur Diagnostik oft rein visuell ausgewertet und ermöglichen zum Beispiel die Diagnose von Schlaganfällen. Im Rahmen von Gruppenstudien werden statistische Unterschiede in diesen Maßen untersucht, zum Beispiel ein Rückgang der Anisotropie bei bestimmten Erkrankungen.

Außerdem wird die Richtung des größten Diffusionskoeffizienten häufig als Farbwert kodiert. Hierbei wird jeder der drei Achsen eine der Grundfarben rot, grün und blau zugeordnet, die bei dazwischen liegenden Richtungen gemischt werden.[4] Voxel ohne klare Hauptrichtung erscheinen grau (siehe Abbildung).

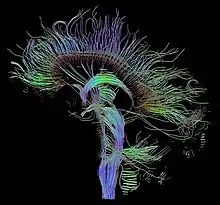
Traktografie

Als Traktografie oder Fiber Tracking werden Verfahren bezeichnet, die den Verlauf größerer Nervenfaserbündel rekonstruieren. Zur Visualisierung sind hierbei Darstellungen von Hyperstromlinien üblich, dreidimensionalen Linien, deren Verlauf der Richtung des größten Diffusionskoeffizienten folgt.[5][6] Die Abbildung am Beginn dieses Artikels zeigt beispielhaft alle Bündel, die die Medianebene schneiden. Einen alternativen Ansatz stellt die probabilistische Traktografie dar. Sie berechnet für jeden Punkt im Gehirn eine Wahrscheinlichkeit, mit der auf Grundlage der Daten eine Nervenverbindung mit einem gegebenen Ausgangsareal angenommen werden kann.[7] Derartige Ergebnisse eignen sich weniger für die Erzeugung aussagekräftiger Bilder, ermöglichen jedoch quantitative Aussagen und finden daher in der Kognitionsforschung Verwendung.

Die Tatsache, dass die Diffusions-Tensor-Bildgebung derzeit das einzige Verfahren ist, das eine nicht-invasive Darstellung der Nervenfaserbündel erlaubt, hat wesentlich zu ihrer Verbreitung beigetragen. Andererseits ist es aufgrund dessen schwierig zu überprüfen, inwiefern die Ergebnisse gängiger Traktografie-Verfahren mit dem tatsächlichen Verlauf der Nervenbahnen übereinstimmen. Erste Versuche der Validierung im Tierexperiment stützen die Vermutung, dass die Hauptrichtung der Diffusion die Ausrichtung kohärenter Nervenfasern anzeigt[8] und weisen Übereinstimmungen zwischen nichtinvasiver Traktografie und nach dem Tod durchgeführten histologischen Untersuchungen nach.[9] Bereiche, in denen Faserbündel sich auffächern oder kreuzen, werden von der DT-MRI nur unzureichend erfasst und motivieren daher ihre Weiterentwicklung zu Methoden mit hoher Winkelauflösung (siehe unten).

Tensor-Glyphen

Als Glyphen werden in der Visualisierung geometrische Körper bezeichnet, deren Form und Ausrichtung die gewünschte Information vermitteln. Sie bieten die Möglichkeit, die in einem Diffusionstensor enthaltene Information vollständig darzustellen. Allerdings kann in diesem Fall nur ein Ausschnitt der Daten gezeigt werden, da Glyphen eine gewisse Größe haben müssen und sich nicht verdecken dürfen, um erkennbar zu bleiben. Die verbreitetsten Tensor-Glyphen sind Ellipsoide, deren Halbachsen mit der Stärke der Diffusion in der jeweiligen Richtung skaliert sind; die längste Halbachse zeigt also in Richtung der stärksten Diffusion. Ist der Diffusionskoeffizient in allen Richtungen etwa gleich, so ähnelt der Diffusions-Ellipsoid einer Kugel (siehe Abbildung).

Anwendungen

Diagnostik

Eine häufige Anwendung von diffusionsgewichteter MRT ist die Schlaganfall-Diagnostik. Das betroffene Hirngewebe weist oft schon nach wenigen Minuten geringere Diffusionskoeffizienten auf als die gesunde Umgebung. Dieser Effekt wird darauf zurückgeführt, dass nach Ausfall der Natrium-Kalium-Pumpen im geschädigten Bereich extrazelluläre Flüssigkeit in die Zellen einströmt, wo ihre Diffusionsbewegung stärkeren Einschränkungen unterliegt.

In herkömmlichen MRT-Bildern wird der Infarkt erst später sichtbar, in manchen Fällen erst nach 8 bis 12 Stunden.[10] Dieser Unterschied ist klinisch bedeutsam, da eine Thrombolyse-Therapie in der Regel nur innerhalb von 3 bis 4,5 Stunden nach Beginn des Infarkts sinnvoll ist.[11]

Operationsplanung

Bei chirurgischen Eingriffen im Gehirn und der Bestrahlung von Hirntumoren ist es wichtig, die Nervenbahnen so weit wie möglich zu erhalten, da ihre Verletzung in der Regel zu bleibenden Funktionsausfällen führt. Die Diffusions-Tensor-Bildgebung kann helfen, vorab die Lage der Nerven festzustellen und bei der Operations- bzw. Bestrahlungsplanung zu berücksichtigen. Da sich das Gehirn während des Eingriffs verformt, kann es sinnvoll sein eine Operation zu unterbrechen, um eine erneute Aufnahme anzufertigen.

Die Diffusions-Tensor-Bildgebung gibt zudem Hinweise darauf, ob ein Tumor bereits in eine Nervenbahn eingedrungen ist und kann in einigen Fällen die Einschätzung unterstützen, ob eine Operation überhaupt aussichtsreich ist.

Forschung

Die Diffusions-Tensor-Bildgebung wird zunehmend als Forschungsinstrument in medizinischen und kognitionswissenschaftlichen Studien eingesetzt. Im Zentrum des Interesses stehen hier meist Veränderungen des mittleren Diffusionskoeffizienten (Mittlere Diffusivität) und der Fraktionalen Anisotropie, wobei letztere häufig als Indikator für die Integrität von Nervenfasern interpretiert wird.

So konnte etwa gezeigt werden, dass normale Alterungsprozesse mit einem signifikanten Rückgang der Fraktionalen Anisotropie und einer Erhöhung der mittleren Diffusivität einhergehen.[12] Auch bei vielen neurologischen und psychiatrischen Krankheiten, darunter Multiple Sklerose, Epilepsie, Morbus Alzheimer, Schizophrenie und HIV-Enzephalopathie, lassen sich Veränderungen in der DT-MRI nachweisen. Viele Studien auf Basis der Diffusion-Bildgebung gehen der Frage nach, welche Hirnregionen besonders betroffen sind. Die Diffusions-Tensor-Bildgebung wird hier auch komplementär zur funktionellen Magnetresonanztomografie eingesetzt.

Die Neurowissenschaft nutzt zudem probabilistische Traktografie-Verfahren, die Hinweise auf Nervenverbindungen zwischen bestimmten Hirnarealen liefern. Dies erlaubt es, den Thalamus weiter zu untergliedern, obwohl er in der herkömmlichen Magnetresonanztomographie als einheitliche Struktur erscheint.[13]

Einen besonderen Schwerpunkt bilden aktuelle Varianten der Diffusions-Bildgebung im Human Connectome Project, dessen Ziel es ist, die natürliche Variabilität des gesunden menschlichen Konnektoms zu untersuchen. Im Rahmen dieses während der Jahre 2010 bis 2015 mit insgesamt knapp 40 Millionen US-Dollar geförderten Programms werden die Ergebnisse der Diffusions-Bildgebung unter anderem mit Genanalysen und kognitiven Fähigkeiten korreliert.

Historische Entwicklung

Der Chemiker Edward O. Stejskal und sein Doktorand John E. Tanner beschrieben bereits 1965, wie sich ein kurzzeitig geschaltetes Gradientenfeld in Kernspinresonanz-Experimenten dazu nutzen lässt, die Diffusionsbewegung von Wasserstoff-Kernen zu messen.[14] Nach ihnen sind sowohl die für die Diffusions-Bildgebung grundlegende Mess-Sequenz benannt, als auch die Formel, die es ermöglicht, aus der Abschwächung des Spin-Echos den Diffusionskoeffizienten zu errechnen.

In den 1970er Jahren schufen Paul Christian Lauterbur und Peter Mansfield mit der ortsaufgelösten Magnetresonanztomografie die Möglichkeit, die Kernspinresonanz zur Bildgebung einzusetzen. 1985 führte der Neuroradiologe Denis LeBihan das von Stejskal und Tanner entwickelte Verfahren zur Diffusionsmessung in die MRT ein. In Zusammenarbeit mit LeBihan schlug der Ingenieurwissenschaftler Peter J. Basser 1994 schließlich den Diffusions-Tensor als Modell vor. Er berücksichtigt die Richtungsabhängigkeit des Diffusionskoeffizienten und erlaubt somit Rückschlüsse auf den Verlauf großer Nervenbahnen. Etwa seit dem Jahr 2000 entwickeln verschiedene Forschergruppen aufwändigere Varianten der Diffusions-Bildgebung, die eine große Zahl von Messungen und/oder eine besonders starke Diffusionswichtung erfordern. Für diese Daten wurde eine Vielzahl neuer Modelle vorgeschlagen, von denen bislang (Stand: 2011) keins eine dem Diffusions-Tensor vergleichbare Verbreitung erfahren hat.

Weiterentwicklung des Verfahrens

Verbesserung der Bildqualität

Diffusionsgewichtete MRT-Messungen bieten häufig nur eine eingeschränkte Bildqualität. Die gegenüber traditioneller MRT höhere Anfälligkeit gegen Störungen erklärt sich aus dem oben beschriebenen Messverfahren: Da sich die Diffusionsbewegung in einer Abschwächung des gemessenen Signals äußert, wird dies stärker vom Rauschen der Mess-Apparatur beeinflusst. Aus diesem Grund gibt es kaum Fortschritte in Richtung einer höheren Ortsauflösung des Verfahrens, da kleinere Volumenelemente ein entsprechend schwächeres Ausgangssignal bieten. Zudem benötigt man eine große Zahl von Einzelmessungen und nutzt daher meist zeitsparende Mess-Sequenzen wie das Echo Planar Imaging, um den Gesamtaufwand und die Belastung des Patienten vertretbar zu halten. Diese Sequenzen führen jedoch besonders häufig zu Artefakten.

Diesen Problemen begegnet man zum einen durch Nachbearbeiten der Messdaten im Computer, wodurch die Störungen zum Teil korrigiert werden können. Die radiologische Forschung sucht außerdem nach neuen MRT-Sequenzen, die weniger fehleranfällig sind.

Erhöhung der Winkelauflösung

Das Diffusions-Tensor-Modell beschreibt das Diffusionsverhalten innerhalb eines Voxels nur dann annähernd korrekt, wenn die Diffusion eine einzige Hauptrichtung besitzt. Somit stößt es in Voxeln, in denen Nervenbahnen sich kreuzen oder auffächern, an seine Grenzen. In den vergangenen Jahren wurden daher Ansätze entwickelt, in sehr vielen (60 und mehr) verschiedenen Richtungen diffusionsgewichtete Aufnahmen zu machen, um komplexes Diffusionsverhalten besser erfassen zu können. Derartige Verfahren bezeichnet man mit der Abkürzung HARDI (High Angular Resolution Diffusion Imaging, „Diffusions-Bildgebung mit hoher Winkelauflösung“).

Verarbeitung und Auswertung der Daten

Auch die Methoden, mit denen die Daten der Diffusions-Bildgebung für medizinische Studien weiterverarbeitet und ausgewertet werden, sind derzeit (Stand: 2011) Gegenstand der Forschung. Frühe Studien nutzten zum Teil sehr einfache Methoden der Bildregistrierung, um aus den Diffusions-Daten abgeleitete Maße über größere Probandengruppen hinweg zu vergleichen. Dies hat sich als problematisch erwiesen, da es schwierig ist, die anatomischen Strukturen verschiedener Individuen perfekt zur Deckung zu bringen und Abweichungen zu irreführenden und widersprüchlichen Studienergebnissen führen können. Neben verbesserten Algorithmen zur Registrierung werden daher derzeit auch Methoden zur statistischen Auswertung entwickelt, die weniger empfindlich auf Registrierungsfehler reagieren.[15]

Literatur

Derek K. Jones (Hrsg.): Diffusion MRI: Theory, Methods, and Applications. Oxford University Press, 2011. ISBN 978-0-19-536977-9 Englischsprachiges Fachbuch, das in Beiträgen internationaler Experten physikalische und biologische Grundlagen, Messmethoden, algorithmische Auswertung, Anwendungen, aktuelle Forschungsthemen und historische Hintergrunde abdeckt.
Bernhard Preim, Dirk Bartz: Visualization in Medicine. Morgan Kaufmann, 2007. ISBN 978-0-12-370596-9 Englischsprachiges Fachbuch. Behandelt in Kapitel 18 Messung, Verarbeitung, Visualisierung und Interpretation von Diffusions-Tensor-Daten.
Charles D. Hansen, Christopher R. Johnson (Hrsg.): Visualization Handbook. Academic Press, 2004. ISBN 978-0-12-387582-2 Englischsprachiges Fachbuch. Behandelt in Kapitel 16 die visuelle Aufbereitung von Diffusions-Tensor-Daten.
Le Bihan D, Mangin JF, Poupon C, Clark CA, Pappata S, Molko N, Chabriat H: Diffusion Tensor Imaging: Concepts and Applications. In: Journal of Magnetic Resonance Imaging. 2001, S. 534–546 (englisch, Diffusion Tensor Imaging: Concepts and Applications (Memento vom 19. Oktober 2013 im Internet Archive) [PDF; 696 kB; abgerufen am 22. Juni 2016] Übersichts-Artikel in Fachzeitschrift).
Joachim Weickert, Hans Hagen (Hrsg.): Visualization and Processing of Tensor Fields. Springer, Berlin 2006. ISBN 3-540-25032-8 Englischsprachiges Fachbuch zur Visualisierung und Verarbeitung von Tensor-Daten, mit einem deutlichen Schwerpunkt auf DT-MRI.
Den Geheimnissen des Gehirns auf der Spur. in: Ärzte-Woche. Wien 16.2002, Nr. 27. ISSN 1862-7137 Allgemein verständlicher Überblick über das Verfahren, deutsch.

Weblinks

Commons: Diffusions-Tensor-Bildgebung – Sammlung von Bildern, Videos und Audiodateien

Informationen des Zentrums für Bildgebung in den Neurowissenschaften (Brain Imaging Center, Frankfurt) zur Funktionsweise der DT-MRI
Pressemitteilung der National Institutes of Health (2000) zu den Möglichkeiten der DT-MRI (englisch)

Einzelnachweise

Christian Beaulieu: The basis of anisotropic water diffusion in the nervous system – a technical review. In: NMR in Biomedicine 2002, 15, S. 435–455.
P.J. Basser, J. Mattiello, D. LeBihan: Estimation of the effective self-diffusion tensor from the NMR spin echo. In: Journal of Magnetic Resonance. Series B. San Diego Cal 103.1994, S. 247–254. ISSN 1064-1866
Sonia Nielles-Vallespin, Choukri Mekkaoui u. a.: In vivo diffusion tensor MRI of the human heart: Reproducibility of breath-hold and navigator-based approaches. In: Magnetic Resonance in Medicine. 70, 2013, S. 454, doi:10.1002/mrm.24488.
S. Pajevic, C. Pierpaoli: Color schemes to represent the orientation of anisotropic tissues from diffusion tensor data. Application to white matter fiber tract mapping in the human brain. In: Magnetic Resonance in Medicine. New York 42.1999,3, S. 526–540. ISSN 0740-3194
S. Mori, B. J. Crain, V. P. Chacko, P. C. M. van Zijl: Three-dimensional tracking of axonal projections in the brain by magnetic resonance imaging. In: Annals of Neurology, 45(2), S. 265–269, 1999
P. J. Basser, S. Pajevic, C. Pierpaoli, J. Duda, A. Aldroubi: In vivo fiber tractography using DT-MRI data. In: Magnetic Resonance in Medicine. New York 44.2000, S. 625–632. ISSN 0740-3194
T.E.J. Behrens, M.W. Woolrich, M. Jenkinson, H. Johansen-Berg, R.G. Nunes, S. Clare, P.M. Matthews, J.M. Brady, S.M. Smith: Characterization and Propagation of Uncertainty in Diffusion-Weighted MR Imaging. In: Magnetic Resonance in Medicine. 50, S. 1077–1088, 2003.
C.-P. Lin, W.-Y. I. Tseng, H.-C. Cheng, J.-H. Chen: Validation of diffusion tensor magnetic resonance axonal fiber imaging with registered manganese-enhanced optic tracts. In: NeuroImage, 14(5), S. 1035–1047, 2001.
J. Dauguet, S. Peled, V. Berezovskii, T. Delzescaux, S. K. Warfield, R. Born, C.-F. Westin: 3D histological reconstruction of fiber tracts and direct comparison with diffusion tensor MRI tractography. In: Medical Image Computing and Computer-Assisted Intervention, Seiten 109–116, Springer, 2006.
K.-O. Lövblad, H.-J. Laubach, A.E. Baird, F. Curtin, G. Schlaug, R.R. Edelman, S. Warach: Clinical Experience with Diffusion-Weighted MR in Patients with Acute Stroke. In: American Journal of Neuroradiology. Oak Brook Ill 19.1998, S. 1061–1066. ISSN 0195-6108
W.Hacke et al.: Trombolysis with Alteplase 3 to 4.5 Hours after Acute Ischemic Stroke. In The New England Journal of Medicine, 359, 2008, S. 1317.
E. V. Sullivan und A. Pfefferbaum: Diffusion Tensor Imaging in Aging and Age-Related Neurodegenerative Disorders. Kapitel 38 in D. K. Jones (Hrsg.): Diffusion MRI: Theory, Methods, and Applications. Oxford University Press, 2011.
T.E.J. Behrens, H. Johansen-Berg u. a.: Non-invasive mapping of connections between human thalamus and cortex using diffusion imaging. In: Nature Neuroscience. New York 6.2003,7, 750-757. ISSN 1097-6256
E.O. Stejskal, J.E. Tanner: Spin Diffusion Measurements – Spin echoes in the presence of a time-dependent field gradient. In: Journal of Chemical Physics. Melville 42.1965, S. 288–292. ISSN 0021-9606
S. M. Smith, M. Jenkinson, H. Johansen-Berg, D. Rueckert, T. E. Nichols, C. E. Mackay, K. E. Watkins, O. Ciccarelli, M. Z. Cader, P. M. Matthews, T. E. J. Behrens: Tract-based spatial statistics: Voxelwise analysis of multi-subject diffusion data. In: NeuroImage. 31(4), S. 1487–1505, 2006.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Christian Beaulieu: The basis of anisotropic water diffusion in the nervous system – a technical review. In: NMR in Biomedicine 2002, 15, S. 435–455.

[2] P.J. Basser, J. Mattiello, D. LeBihan: Estimation of the effective self-diffusion tensor from the NMR spin echo. In: Journal of Magnetic Resonance. Series B. San Diego Cal 103.1994, S. 247–254. ISSN 1064-1866

[3] Sonia Nielles-Vallespin, Choukri Mekkaoui u. a.: In vivo diffusion tensor MRI of the human heart: Reproducibility of breath-hold and navigator-based approaches. In: Magnetic Resonance in Medicine. 70, 2013, S. 454, doi:10.1002/mrm.24488.

[4] S. Pajevic, C. Pierpaoli: Color schemes to represent the orientation of anisotropic tissues from diffusion tensor data. Application to white matter fiber tract mapping in the human brain. In: Magnetic Resonance in Medicine. New York 42.1999,3, S. 526–540. ISSN 0740-3194

[5] S. Mori, B. J. Crain, V. P. Chacko, P. C. M. van Zijl: Three-dimensional tracking of axonal projections in the brain by magnetic resonance imaging. In: Annals of Neurology, 45(2), S. 265–269, 1999

[6] P. J. Basser, S. Pajevic, C. Pierpaoli, J. Duda, A. Aldroubi: In vivo fiber tractography using DT-MRI data. In: Magnetic Resonance in Medicine. New York 44.2000, S. 625–632. ISSN 0740-3194

[7] T.E.J. Behrens, M.W. Woolrich, M. Jenkinson, H. Johansen-Berg, R.G. Nunes, S. Clare, P.M. Matthews, J.M. Brady, S.M. Smith: Characterization and Propagation of Uncertainty in Diffusion-Weighted MR Imaging. In: Magnetic Resonance in Medicine. 50, S. 1077–1088, 2003.

[8] C.-P. Lin, W.-Y. I. Tseng, H.-C. Cheng, J.-H. Chen: Validation of diffusion tensor magnetic resonance axonal fiber imaging with registered manganese-enhanced optic tracts. In: NeuroImage, 14(5), S. 1035–1047, 2001.

[9] J. Dauguet, S. Peled, V. Berezovskii, T. Delzescaux, S. K. Warfield, R. Born, C.-F. Westin: 3D histological reconstruction of fiber tracts and direct comparison with diffusion tensor MRI tractography. In: Medical Image Computing and Computer-Assisted Intervention, Seiten 109–116, Springer, 2006.

[10] K.-O. Lövblad, H.-J. Laubach, A.E. Baird, F. Curtin, G. Schlaug, R.R. Edelman, S. Warach: Clinical Experience with Diffusion-Weighted MR in Patients with Acute Stroke. In: American Journal of Neuroradiology. Oak Brook Ill 19.1998, S. 1061–1066. ISSN 0195-6108

[11] W.Hacke et al.: Trombolysis with Alteplase 3 to 4.5 Hours after Acute Ischemic Stroke. In The New England Journal of Medicine, 359, 2008, S. 1317.

[12] E. V. Sullivan und A. Pfefferbaum: Diffusion Tensor Imaging in Aging and Age-Related Neurodegenerative Disorders. Kapitel 38 in D. K. Jones (Hrsg.): Diffusion MRI: Theory, Methods, and Applications. Oxford University Press, 2011.

[13] T.E.J. Behrens, H. Johansen-Berg u. a.: Non-invasive mapping of connections between human thalamus and cortex using diffusion imaging. In: Nature Neuroscience. New York 6.2003,7, 750-757. ISSN 1097-6256

[14] E.O. Stejskal, J.E. Tanner: Spin Diffusion Measurements – Spin echoes in the presence of a time-dependent field gradient. In: Journal of Chemical Physics. Melville 42.1965, S. 288–292. ISSN 0021-9606

[15] S. M. Smith, M. Jenkinson, H. Johansen-Berg, D. Rueckert, T. E. Nichols, C. E. Mackay, K. E. Watkins, O. Ciccarelli, M. Z. Cader, P. M. Matthews, T. E. J. Behrens: Tract-based spatial statistics: Voxelwise analysis of multi-subject diffusion data. In: NeuroImage. 31(4), S. 1487–1505, 2006.