Boundary Representation
Boundary Representation, auf deutsch Begrenzungsflächenmodell, (B-rep oder Brep) ist eine Darstellungsform eines Flächen- oder Volumenmodells, in der Objekte durch ihre begrenzenden Oberflächen beschrieben werden. Der Begriff setzt sich aus den englischen Worten boundary für Begrenzung, Rand und representation für Darstellung zusammen.
Anwendung
Visualisierung
Boundary Representation Modelle finden bevorzugt in der Visualisierung von 3D-Computergrafik und bei CAD-Programmen ihre Anwendung, da sie algorithmisch schnell verarbeitbar sind.
Volumenmodellierung
Mit dem Boundary Representation Modell lassen sich auch Volumenmodelle beschreiben. Da hierbei ein Körper nur durch seine berandenden Oberflächen dargestellt wird, spricht man von einer indirekten Modellierung (im Gegensatz zur direkten Modellierung mit Constructive Solid Geometry, bei der mit Körpern konstruiert wird). Der Anwender oder ein intelligenter Prüfalgorithmus muss dabei sicherstellen, dass es sich um eine geschlossene Hülle handelt.
Objekterzeugung
Die Definition von Instanzen kann mit einem Knoten-Kanten-Flächen-Graph (vef-Graph, engl. vertex, edge, face) erfolgen. Die Geometrie wird hierbei durch die Koordinaten der Punkte festgelegt. Die Topologie, also die Beziehungen zwischen den Punkten, beschreiben die Kanten und Flächen. Kanten referenzieren dabei auf Punkte und Flächen auf Kanten.
Beispiel
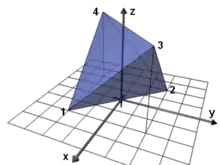
Beispielhaft wird für ein Tetraeder ein vef-Graph aufgebaut. Die Speicherung der Informationen geschieht mit einem relationalen Datenbankmodell. Die Beschreibung des Objektes kann auf vielerlei Weisen geschehen. Hier werden dazu folgende drei Listen definiert:
- Die Knotenliste, welche die Koordinaten der Punkte enthält,
- die Kantenliste, welche für jede Kante auf zwei Punkte referenziert, und
- die Flächenliste, welche für jede Fläche eine geschlossene Kantenfolge besitzt.
Um eine Eindeutigkeit zu erreichen, legt man den Umlaufsinn der Kantenfolge mit der Definition, die Fläche sei z. B. links davon, fest. So ist es im 2D möglich, mit gegensätzlicher Umlaufrichtung Löcher zu beschreiben. Im 3D bestimmt sich damit über die Drei-Finger-Regel die Flächennormale, welche wiederum zur Festlegung der „Vorderseite“ herangezogen werden kann. Zu beachten ist, dass dabei nicht die Reihenfolge der Punkte, sondern der Kanten ausgewertet wird.
| Knotennummer | x | y | z |
|---|---|---|---|
| 1 | 2 | −2 | 0 |
| 2 | −2 | 2 | 0 |
| 3 | 2 | 2 | 4 |
| 4 | −2 | −2 | 4 |
| Kantennummer | Knotennummer 1 | Knotennummer 2 |
|---|---|---|
| 1 | 1 | 2 |
| 2 | 2 | 3 |
| 3 | 1 | 3 |
| 4 | 1 | 4 |
| 5 | 2 | 4 |
| 6 | 3 | 4 |
| Flächennummer | Kantenfolge (Kantennummer 1, Kantennummer 2, …) |
|---|---|
| 1 | 1 2 3 |
| 2 | 3 6 4 |
| 3 | 2 5 6 |
| 4 | 1 4 5 |
Möchte man ein Volumenmodell beschreiben, ist noch eine vierte Tabelle notwendig, die alle umschließenden Flächen aufzählt. Der Anwender muss – wie oben erwähnt – dafür Sorge tragen, dass die Teilflächen das Volumen vollständig umgrenzen und keine Lücken verbleiben. Der Eintrag der Spalte „Orientierung“ legt fest, ob der Normalenvektor der ersten in der Liste der Begrenzungsflächen angegebenen Fläche vom Volumen weg oder in das Volumen hinein zeigt. Wie im 2D für Flächen lassen sich so Löcher modellieren.
| Volumennummer | Orientierung | Begrenzungsflächen (Flächennummer 1, Flächennummer 2, …) |
|---|---|---|
| 1 | 1 | 1 2 3 4 |
Siehe auch
Literatur
- Christoph Martin Hoffmann: Geometric & Solid Modeling. Morgan Kaufmann Publishers, San Mateo, California 1989, ISBN 1-55860-067-1.
- Martii Mäntylä: An Introduction to Solid Modeling. Computer Science Press, Rockville, Maryland 1988, ISBN 0-88175-108-1.