Polygonnetz

Untereinander mit Kanten verbundene Punkte bilden in der Computergrafik ein Polygonnetz, das die Gestalt eines Polyeders definiert. Dreiecksnetze und Vierecksnetze sind hier am geläufigsten. Zur Speicherung von Polygonnetzen und Polygonen gibt es eine Reihe bekannter Datenstrukturen. Die bekanntesten Strukturen sind die Knotenliste, Kantenliste, Winged Edge und die doppelt verkettete Kantenliste (doubly connected halfedge list).

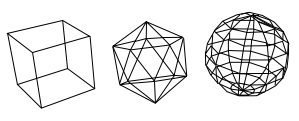
Unterschiedliche Drahtgittermodelle, die einfachste Möglichkeit, ein Polygonnetz darzustellen.

Jeder Knoten muss mindestens eine Verbindung zum Restnetz haben, um Mitglied des Netzes zu sein. Daraus folgt, dass jeder Knoten von jedem anderen im Netz erreichbar ist. In der Graphentheorie sind Polygonnetze als ungerichtete Graphen ohne Mehrfachkanten darstellbar.[1][2]

Eigenschaften von Polygonnetzen

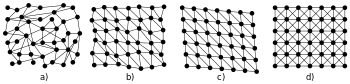
Das Bild zeigt typische Netzeigenschaften an verschiedenen Polygonnetzen: a) Zeigt ein Polygonnetz ohne besondere Eigenschaften, b) ein strukturiertes Polygonnetz, c) zeigt ein Polygonnetz, das strukturiert und regulär ist, und d) ist strukturiert, regulär und orthogonal.

Folgende Eigenschaften kann ein Netz haben, keine davon ist allerdings für ein Polygonnetz erforderlich:[1]

Strukturiertheit: Ein Polygonnetz wird als strukturiert bezeichnet, wenn jeder innere Punkt die gleiche Anzahl anliegender Kanten und Flächen hat.
Regularität: Ein Polygonnetz ist regulär, wenn die Kantenlängen in jede Richtung konstant sind. Diese Eigenschaft baut auf der Strukturiertheit auf.
Orthogonalität: Ein Polygonnetz wird als orthogonal bezeichnet, wenn die Netzkanten rechte Winkel bilden. Die Orthogonalität baut auf die Eigenschaft der Strukturiertheit und der Regularität auf.

Polygonnetz als Dreiecksnetz

Das Polygonnetz als Dreiecksnetz ist eine weit verbreitete Form des Polygonnetzes. Es ist vor allem bei Triangulationen und beim Meshing von Bedeutung.

(TIN)

Datenstrukturen

Knotenliste

Bei der Knotenliste werden die Punkte in einer separaten Punktliste abgelegt. Eine Fläche wird dann als eine Liste von Zeigern auf die Punkte in dieser Liste definiert. Dadurch wird eine Trennung zwischen der Geometrie (den Koordinaten der Knoten) und der Topologie (welche Knoten verbinden welche Kanten, welche Kanten begrenzen welche Flächen) realisiert.

Kantenliste

Die Nachteile der Knotenliste werden bei der Kantenliste dadurch umgangen, dass alle Kanten in einer separaten Liste gespeichert werden. Facetten werden hier als Zeiger auf die Kantenliste definiert. Neben dem Anfangs- und Endpunkt werden auch die maximal zwei zugehörigen Facetten für jede Kante abgelegt. Die Reihenfolge der Angabe der Eckpunkte für Kanten legt eine Orientierung fest und bestimmt bei Facetten, wo innen und wo außen ist.

Vor- bzw. Nachteile

Datenstruktur	Vorteile	Nachteile
Knotenliste	Trennung von Geometrie und Topologie minimale Redundanzen (Punkte werden nur einmal abgelegt)	Kanten werden mehrmals durchlaufen und ausgegeben Suche nach zu Kanten gehörenden Facetten nicht effizient möglich (nur mit erschöpfender Suche möglich) Für alle Kanten in F1 (jedes Knotenpaar) suchen wir in allen weiteren Facetten, ob sie enthalten ist, wenn nein, dann Randkante Suchen nach Facetten, welche eine Kante bzw. Ecke enthalten, ist ineffizient
Kantenliste	Trennung von Geometrie und Topologie Schnelle Bestimmung von Randkanten (Kanten mit nur einem Verweis auf Facette)	Suchen nach Facetten, welche eine Kante bzw. Ecke enthalten, ist ineffizient

Generell gilt für Knoten- und Kantenlisten, dass die Suche ausgehend von einer Facette nach untergeordneten Objekten wie Kanten und Knoten sehr effizient durchführbar ist. In umgekehrter Richtung verhält es sich jedoch gegenteilig. So ist z. B. die Suche nach allen Facetten, welche eine bestimmte Ecke enthalten, immer noch nur durch eine erschöpfende Suche möglich.

Winged Edge nach Baumgart

Eine Datenstruktur, mit deren Hilfe sehr viele Abfragen effizient bearbeitet werden können, ist die Winged-Edge-Darstellung nach Baumgart. Zusätzlich zu den Informationen der Kantenliste werden hier noch Zeiger auf die Kanten abgelegt, die von Anfangs- und Endpunkt der aktuellen Kante abgehen. Aufgrund der Orientierung wird jede Kante einmal positiv (im Uhrzeigersinn) und einmal negativ (gegen den Uhrzeigersinn) durchlaufen.

Mit der Winged-Edge-Datenstruktur ist es möglich, in konstanter Zeit abzufragen, welche Knoten oder Facetten zu einer gegebenen Kante gehören. Hat eine Facette k Kanten, können in linearer Zeit diese Kanten nacheinander abgesucht werden (nur bei polygonalen Netzen ohne Änderung der Durchlaufrichtung eines Polygons). Andere Anfragen, insbesondere solche ausgehend von einer Ecke, die nach den Kanten oder Facetten, in denen diese Ecke enthalten ist, suchen, sind deutlich langsamer.

Doppelt verkettete Kantenliste (Half Edge)

Die Half-Edge-Datenstruktur ist ein wenig ausgereifter als die Winged-Edge-Liste. Sie erlaubt, die meisten in der folgenden Tabelle aufgeführten Operationen in konstanter Zeit auszuführen, d. h. konstanter Zeit pro gesammelte Information. Wenn man z. B. alle zu einem Eckpunkt benachbarten Kanten herausfinden will, ist die Operation linear bezüglich der Anzahl der benachbarten Kanten aber konstant in der Zeit pro Kante. Half Edge funktioniert nur mit zweidimensionaler Mannigfaltigkeit, d. h. jede Kante ist von genau zwei Facetten (zu jeder Halbkante gibt es eine entgegengesetzte Halbkante) umgeben, d. h. T-Verbindungen, innere Polygone und Brüche sind nicht erlaubt.

Bei der Half-Edge-Struktur werden nicht Kanten, sondern Halbkanten abgelegt. Halbkanten sind gerichtet und zwei zusammengehörende Halbkanten (Paar) bilden eine Kante und zeigen in die entgegengesetzte Richtung.

Eine weitere Datenstruktur ist die Doubly-connected edge list (DCEL).

Laufzeitvergleich

Folgende Tabelle zeigt einen Vergleich der asymptotischen Laufzeit in Abhängigkeit von den vorhandenen Elementen Knoten, Kanten und Flächen. Es gibt neun mögliche Abfragen auf die Struktur, nämlich „welche Ecke, Kante oder Fläche gehört zu welcher Ecke Kante oder Fläche“. Alle Abfragen bis auf diejenige nach den benachbarten Ecken einer gegebenen Ecke werden in der Tabelle aufgeführt. Der Vergleich zeigt, wie unterschiedlich gut die Datenstrukturen die Anfrageklassen bearbeiten.

Suchanfrage (gegeben → gesucht)	Knotenliste	Kantenliste	Winged Edge	Half Edge
Kante → Eckpunkte	N/A	${\mathcal {O}}(1)$	${\mathcal {O}}(1)$	${\mathcal {O}}(1)$
Kante → Facetten	N/A	${\mathcal {O}}(1)$	${\mathcal {O}}(1)$	${\mathcal {O}}(1)$
Kante → angrenzende Kanten	N/A	${\mathcal {O}}(k)$	${\mathcal {O}}(k)$	${\mathcal {O}}(k_{v})$
Eckpunkt → Kanten	${\mathcal {O}}(f*k_{f})$	${\mathcal {O}}(k)$	${\mathcal {O}}(k)$	${\mathcal {O}}(k_{v})$
Eckpunkt → Facetten	${\mathcal {O}}(f*k_{f})$	${\mathcal {O}}(k)$	${\mathcal {O}}(k)$	${\mathcal {O}}(k_{v})$
Facette → Kanten	${\mathcal {O}}(k_{f})$	${\mathcal {O}}(k_{f})$	${\mathcal {O}}(k_{f})$	${\mathcal {O}}(k_{f})$
Facette → Eckpunkte	${\mathcal {O}}(k_{f})$	${\mathcal {O}}(k_{f})$	${\mathcal {O}}(k_{f})$	${\mathcal {O}}(k_{f})$
Facette → benachbarte Facette	${\mathcal {O}}(f*k_{f}^{2})$	${\mathcal {O}}(k_{f})$	${\mathcal {O}}(k_{f})$	${\mathcal {O}}(k_{f})$

Hierbei bezeichnet:

$k$ : Anzahl aller Kanten
$k_{f}$ : Anzahl der Kanten einer Facette
$k_{v}$ : Anzahl der Kanten, welche zu einem Punkt gehören
$f$ : Anzahl aller Facetten

Erläuterung der Anfrageklassen

Anfrage	Knotenliste	Kantenliste	Winged Edge	Half Edge
Kante → Eckpunkte	Nicht möglich (es gibt keine Kanten)	direkt über Kanten ablesbar	direkt über Eintrag für Kante abzulesen	über Halbkante→vert und pair→vert.
Kante → Facetten	Nicht möglich (es gibt keine Kanten)	direkt aus Kanten ablesbar	direkt aus Kante ersichtlich	die angrenzenden Flächen über edge→face und edge→pair→face bestimmen.
Kante → angrenzende Kanten	Nicht möglich (es gibt keine Kanten)	für beide Eckpunkte: „Eckpunkt → Kante“ durchführen	siehe Kantenliste	siehe Kantenliste
Eckpunkt → Kanten	Da es sich um geschlossene Polygone handelt, hat jede Facette (genauso viele Kanten wie Punkte) Kanten, diese müssen zu jeder Fläche bestimmt werden und nachgeschaut werden, ob die gegebene Ecke darin enthalten ist	einfach alle Kanten durchlaufen	Startkante zum Punkt ermitteln, dann über „Vorgänger rechts“ suchen solange bis keine Kante mehr da ist, dann wieder bei Startkante beginnen und in andere Richtung laufen.	über vert→edge erste Kante holen, danach entgegengesetzte Kante holen und links weiterlaufen. Dies so lange machen, bis links keine Nachfolgerkante da ist, dann wieder mit vert→edge anfangen und diesmal so lange nach rechts laufen, bis keine Nachbarkante mehr vorhanden ist.
Eckpunkt → Facetten	Einfach für alle Facetten die Kanten durchgehen, und schauen, ob der gesuchte Eckpunkt enthalten ist.	„Eckpunkt → Kante“ ausführen und aus diesen Kanten dann direkt die zugehörige Facette lesen.	einfach nur die Kanten zum Punkt ermitteln und in konstanter Zeit die dazugehörigen Flächen ermitteln	siehe Kantenliste
Facette → Kanten	Alle Kanten einer Facette jeweils paarweise bilden	direkt aus Facetten ablesbar	siehe Half Edge	Bei Startkante der Facette beginnen und nach links laufen. Gehört die nachfolgende Kante zur selben Facette, dann in gleicher Laufrichtung weitermachen. Wird das erste Mal kein Nachfolger gefunden, kehrt man die Laufrichtung um. Gehört der Nachfolger zur selben Facette, dann in dieser Laufrichtung weitermachen, ansonsten abbrechen. Die Laufrichtung kann sich mehrmals ändern. Irgendwann kommt man bei der Startkante an. Dann kann man aufhören.
Facette → Eckpunkte	Einfach direkt aus Facetten auslesen	„Facette → Kanten“ ausführen und in konstanter Zeit die zugehörigen Eckpunkte auslesen	siehe Half Edge	„Facette → Kanten“ ausführen und aus den Kanten die Punkte herauslesen, doppelte Punkte rausschmeißen.
Facette → benachbarte Facette	Alle Kanten der zu überprüfenden Facette ermitteln und für jede Kante schauen, ob die anderen Facetten diese Kante auch enthalten.	„Facette → Kanten“ ausführen und dann direkt aus den Kanten die zugehörigen Facetten ablesen	„Facette → Kanten“ ausführen und zu jeder Kante die angrenzende Fläche auslesen	siehe Winged Edge

Zusammenfassung

Wie man sieht, sind die Winged-Edge- und die Half-Edge-Struktur von den enthaltenen Informationen nahezu identisch. Sie weisen deshalb auch fast die gleichen Laufzeiten für das Suchen auf. Half Edge ist in den komplexeren Anfragen etwas besser. Hier müssen aufgrund des Zeigers eines Punktes auf eine zugehörige Startkante beim Suchen aller Kanten eines Punktes auch nur diese angefasst werden. Die Knotenliste scheidet von vornherein aus und die Kantenliste ist vom Suchen her genauso gut wie die Winged-Edge-Liste, benötigt jedoch etwas mehr Speicherplatz, da bei Winged Edge zu einer Facette nur eine Startkante abgelegt werden muss.

Siehe auch

Weblinks

Polygon Mesh Processing Library

Einzelnachweise

Jens Neumann: Verfahren zur adhoc-Modellierung und -Simulation räumlicher Feder-Masse-Systeme für den Einsatz in VirtualReality-basierten Handhabungssimulationen. Technische Universität Berlin, Fraunhofer IRB Verlag, 2009, ISBN 978-3-8167-7954-4.
Oliver Burgert: Modellbildung II – Nodale Netze – Medizinische Planungs- und Simulationssysteme. (Memento des Originals vom 10. August 2007 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2Vorlage:Webachiv/IABot/www.iccas.de (PDF) Universität Leipzig, 2005.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[neumann-1] Jens Neumann: Verfahren zur adhoc-Modellierung und -Simulation räumlicher Feder-Masse-Systeme für den Einsatz in VirtualReality-basierten Handhabungssimulationen. Technische Universität Berlin, Fraunhofer IRB Verlag, 2009, ISBN 978-3-8167-7954-4.

[bur-2] Oliver Burgert: Modellbildung II – Nodale Netze – Medizinische Planungs- und Simulationssysteme. (Memento des Originals vom 10. August 2007 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2Vorlage:Webachiv/IABot/www.iccas.de (PDF) Universität Leipzig, 2005.