UNIFAC

UNIFAC[1][2] (Abkürzung für Universal Quasichemical Functional Group Activity Coefficients) ist ein Verfahren zur Abschätzung von Aktivitätskoeffizienten, das in der Verfahrenstechnik und der Technischen Chemie häufig eingesetzt wird.

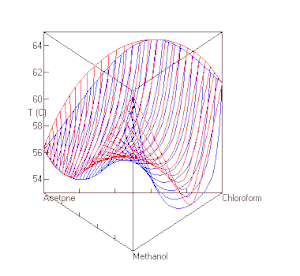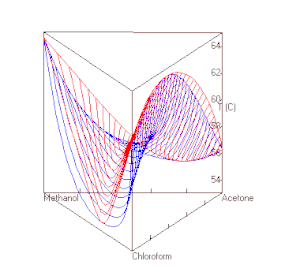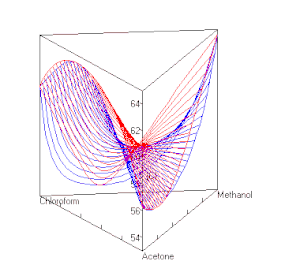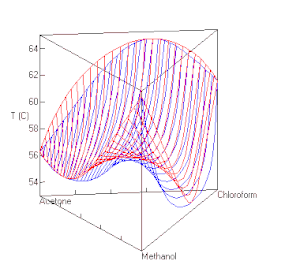
Dampf-Flüssig-Gleichgewicht mit Sattelazeotrop
berechnet mit UNIFAC bei P=1 atm. Die roten Linien sind Dampfzusammensetzungen, die blauen die Zusammensetzung der Flüssigkeit.

UNIFAC ist von UNIQUAC abgeleitet. UNIQUAC verwendet stoffspezifische Parameter, die aus experimentell ermittelten Daten bestimmt werden müssen. Diese Parameter werden in UNIFAC vorhergesagt, so dass keine gemessenen Daten mehr benötigt werden.

Prinzipien

UNIFAC ist eine Gruppenbeitragsmethode, die auf dem Prinzip der Mischung aus Strukturgruppen basiert. Dies steht im Gegensatz zu der normalen Betrachtungsweise der Mischung aus Molekülen. Die Gruppen sind dabei üblicherweise funktionelle Gruppen, bspw. Alkohol- oder Carbonylgruppe, aber auch kleinere Molekülfragmente wie einzelne Atome, jedoch werden diese kleinen Fragmente stets unter Berücksichtigung ihrer chemischen Umgebung betrachtet. Einige wenige kleinere Moleküle (etwa Wasser) werden vollständig als eigenständige Gruppe definiert.

Gruppenbeitragsmethodenprinzip

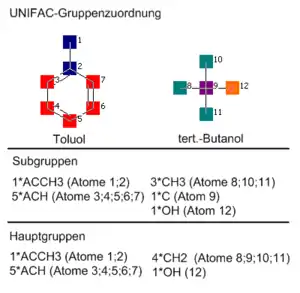
Beispiel einer Gruppenzuordnung in UNIFAC

Das Prinzip der Gruppenbeitragsmethoden besteht im Wesentlichen darin, dass nur die Eigenschaften einiger Dutzend Strukturgruppen bekannt sein müssen, statt die Eigenschaften von einigen Millionen Stoffen für die Berechnung von Stoffgemischeigenschaften zu benötigen. Mit diesen wenigen Strukturgruppen als Bausteinen kann eine sehr große Anzahl von Molekülen konstruiert werden.

UNIFAC-Gruppenbeiträge

UNIFAC benutzt zur Vorhersage zwei Arten von Gruppenbeiträgen:

Additive Beiträge, die sehr kleinen Gruppen (Untergruppen) zugeordnet werden. Dies sind Gruppenvolumina und Gruppenoberflächen.
Wechselwirkungsparameter zwischen größeren Gruppen, die mehrere ähnliche Untergruppen umfassen.

Die Gruppenvolumina- und oberflächen basieren auf angenäherten van der Waalsschen Oberflächen und Volumina[3] und sind somit Konstanten im Modell, die einen physikalisch-chemischen Hintergrund haben.

Die Wechselwirkungsparameter werden an experimentelle Aktivitätskoeffizienten sowie an Phasengleichgewichtsdaten, aus denen Aktivitätskoeffizienten abgeleitet werden können, mit nichtlinearen Optimierverfahren angepasst. Die Wechselwirkungsparameter werden somit ausschließlich empirisch ermittelt.

Aktuelle Parametrisierung

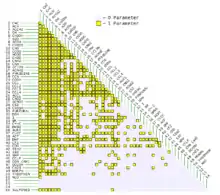
UNIFAC-Parametermatrix (letzte veröffentlichte Version[4])

Das UNIFAC-Modell erlaubt die Vorhersage von Aktivitätskoeffizienten in Gemischen mit Alkanen, Alkenen, Alkinen, Alkoholen, Aromaten, Estern, Ethern, Aminen, Carbonsäuren, organischen Fluoriden, organischen Chloriden, organischen Bromiden, organischen Iodiden, Thiolen, Sulfonen, Wasser, Furfural, Thiophenen, Pyridinen, Morpholin, Isocyanaten, Silanen, Siloxanen, Amiden und organischen Nitraten.

Für diese funktionellen Gruppen sind Wechselwirkungsparameter mit mindestens einer der anderen Gruppen vorhanden. Es sind jedoch nicht alle Kombinationen vollständig parametrisiert, bspw. kann ein Aktivitätskoeffizient eines Gemisch aus 3-Methylthiophen und n-Hexan berechnet werden, eine Vorhersage eines Aktivitätskoeffizienten in einem Gemisch des Thiophens mit 3-Hexen scheitert jedoch an fehlenden Parametern.

UNIFAC kann nicht verwendet werden, um Aktivitätskoeffizienten in Gemischen zu berechnen, die Salze bzw., allgemeiner, Elektrolyte oder Polymere enthalten. Für diese beiden Stoffklassen gibt es aber Erweiterungen des hier beschriebenen UNIFAC-Modells.

Gleichungen

Ausführliche Formulierungen können im Originalartikel gefunden werden oder auch in Lehrbüchern.[5][6]

Die Berechnung des Aktivitätskoeffizienten erfolgt additiv über zwei Terme:

$\ln \gamma _{i}=\ln \gamma _{i}^{C}+\ln \gamma _{i}^{R}$

Kombinatorischer Anteil

γ^C wird als kombinatorischer Anteil bezeichnet und wird aus van der Waalsschen Oberflächen (F) und Volumina (V) sowie Molenbrüchen (x) berechnet.

$\ln \gamma _{i}^{C}=1-V_{i}+\ln V_{i}-5q_{i}\left(1-{{V_{i}} \over {F_{i}}}+\ln {{V_{i}} \over {F_{i}}}\right)$

mit

$V_{i}={{r_{i}} \over {\sum _{j}{r_{j}x_{j}}}}$

$F_{i}={{q_{i}} \over {\sum _{j}{q_{j}x_{j}}}}$

Neben den Molenbrüchen werden van der Waalsche Oberflächen q_i und Volumina r_i der Moleküle benötigt. Diese lassen sich aus tabellierten Werten für die Gruppen (Gruppenoberfläche Q_k und Gruppenvolumen R_k) bestimmen.

$q_{i}=\sum {\nu _{k}^{(i)}Q_{k}}$

$r_{i}=\sum {\nu _{k}^{(i)}R_{k}}$

ν_k⁽ⁱ⁾ ist die Häufigkeit der Gruppe k im Molekül i.

Restanteil

γ^R wird als Restanteil bezeichnet und wird schlussendlich aus angepassten Wechselwirkungsparametern berechnet.

Der Restanteil wird aus Gruppenaktivitätskoeffizienten Γ_k berechnet.

$\ln \gamma _{i}^{R}=\sum _{k}{\nu _{k}^{(i)}\left(\ln \Gamma _{k}-\ln \Gamma _{k}^{(i)}\right)}$

Die Gruppenaktivitätskoeffizienten in der Mischung Γ_k und im Reinstoff Γ_k⁽ⁱ⁾ werden über die Beziehung

$\ln \Gamma _{k}=Q_{k}\left[1-\ln \left(\sum _{m}{\Theta _{m}\Psi _{mk}}\right)-\sum _{m}{{\Theta _{m}\Psi _{km}} \over {\sum _{n}{\Theta _{n}\Psi _{nm}}}}\right]$

berechnet.

Θ ist der Oberflächenanteil

$\Theta _{m}={{Q_{m}X_{m}} \over {\sum _{m}{Q_{m}X_{m}}}}$

und X der Gruppenmolenbruch.

$X_{m}={{\sum _{j}{\nu _{m}^{(j)}x_{j}}} \over {\sum _{j}\sum _{m}{\nu _{n}^{(j)}x_{j}}}}$

Der Parameter ψ enthält die anpassbaren Parameter des UNIFAC-Modells.

$\Psi _{nm}=\exp {\frac {-a_{nm}}{T}}$ mit a_nm als Wechselwirkungsparameter zwischen den Gruppen.

Beispielrechnung

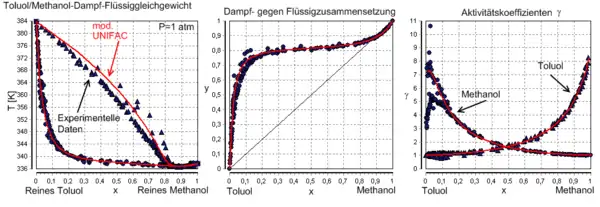
Die Bilder zeigen das Dampf-Flüssiggleichgewicht des Gemischs aus Toluol und Methanol. Die roten Linien zeigen die mit (mod.) UNIFAC berechneten Daten. Für dieses System zeigt die Berechnung eine sehr gute Übereinstimmung mit den experimentell ermittelten Daten.

Geschichte

UNIFAC wurde in den 1970er Jahren entwickelt, wobei der Schwerpunkt zu Beginn alleine auf die Vorhersage von Dampf-Flüssig-Gleichgewichten von Mischungen einfacher, im Wesentlichen organischer Substanzen und von Wassergemischen gelegt wurde. Da für die Modellentwicklung Aktivitätskoeffizienten für eine Vielzahl von Gemischen benötigt wurden, wurde mit dem Aufbau einer Faktendatenbank (der Dortmunder Datenbank) begonnen, die noch heute existiert, wenn auch in stark erweiterter und veränderter Form.

Da Aktivitätskoeffizienten es auch erlauben, mit einfachen thermodynamischen Beziehungen Fest-Flüssig-Gleichgewichte (Löslichkeiten von Feststoffen in Flüssigkeiten) und Flüssig-Flüssig-Gleichgewichte (siehe hierzu Mischungslücke) zu berechnen, wurde das UNIFAC-Modell in den achtziger Jahren auch zunehmend für die Berechnung dieser Phasengleichgewichte verwendet. Die dabei zutage tretenden Modellschwächen des Originalmodells führte zum einen zur Entwicklung von speziell parametrisierten Modellen für die Berechnung von Flüssig-Flüssig-Gleichgewichten (UNIFAC-LLE) und später zu einem Modell für die Abschätzung von Octanol-Wasser-Verteilungskoeffizienten.[7] Zum anderen wurde das Modell selbst erweitert, bspw. um temperaturabhängige Wechselwirkungsparameter:

$\psi =\exp \left({{\frac {-a_{nm}}{T}}+{\frac {-b_{nm}\cdot T}{T}}+{\frac {-c_{nm}\cdot T^{2}}{T}}}\right)$

Diese erweiterten Modelle werden als modifizierte UNIFAC-Modelle[8] bezeichnet.

Bedeutung

UNIFAC (insbesondere die neueren Varianten) ist heute das am häufigsten verwendete Verfahren zur Abschätzung von Stoffgemischdaten. Die Vorhersagen werden bspw. in der Prozesssimulation verwendet, dem heute vorherrschenden Verfahren zur Auslegung und Optimierung chemischer Prozesse, Anlagen und ganzer Fabriken. UNIFAC wird außerdem bei der Prozesssynthese verwendet, bei dem, sehr allgemein formuliert, Stoffe mit bestimmten Eigenschaften für bestimmte Aufgaben gesucht werden. Diese Aufgabe kann bspw. die eines Schleppmittels für die Azeotrop- oder Extraktivrektifikation sein.

Aktuelle Entwicklungen

UNIFAC wird in einer Reihe von Forschungsgruppen genutzt und weiterentwickelt. Aktuelle Entwicklungen (Auswahl) zielen auf

die Berechnung von Elektrolyt-haltigen Mischungen[9]
die Abschätzung von Viskositäten[10]
die Integration von UNIFAC in Mischungsregeln für Zustandsgleichungen (PSRK)[11]
die Vorhersage von UNIFAC-Wechselwirkungsparametern[12]
die Erweiterung des UNIFAC-Modells auf spezielle Stoffgruppen[13]
die Ableitung des UNIFAC-Modells zur Vorhersage von Verdampfungsenthalpien und Exzessenthalpien: Gruppenbeitragsmodelle UNIVAP & EBGCM[14]
die Überarbeitung von Wechselwirkungsparametern für bestehende Gruppen und die Ergänzung von Wechselwirkungsparametern für neue funktionelle Gruppen, um die Anwendbarkeit und die Qualität des UNIFAC-Modells zu verbessern (UNIFAC-Konsortium).

Literatur

A. Fredenslund, R. L. Jones, J. M. Prausnitz: Group-Contribution Estimation of Activity Coefficients in Nonideal Liquid Mixtures. In: AIChE J. 21(6), 1975, S. 1086–1099.
Å. Fredenslund, J. Gmehling, P. Rasmussen: Vapor-Liquid Equilibria Using UNIFAC - A Group Contribution Method. Elsevier, Amsterdam 1977.
A. Bondi: van der Waals Volumes and Radii. In: J.Phys.Chem. 68(3), 1964, S. 441–451.
R. Wittig, J. Lohmann, J. Gmehling: Vapor-Liquid Equilibria by UNIFAC Group Contribution. 6. Revision and Extension. In: Ind.Eng.Chem.Res. 42(1), 2003, S. 183–188.
J. Gmehling, B. Kolbe: Thermodynamik. 2. Auflage. VCH-Verlag, Weinheim 1992.
J. Vidal: Thermodynamique. Méthodes appliquées au raffinage et au Génie Chimique. Editions Technip, 1997.
Gudrun Wienke: Messung und Vorausberechnung von n-Octanol/Wasser-Verteilungskoeffizienten. Doktorarbeit. Univ. Oldenburg, 1993, S. 1–172.
U. Weidlich, J. Gmehling: A Modified UNIFAC Model. 1. Prediction of VLE, hE, and γ^∞. In: Ind.Eng.Chem.Res. 26(7), 1987, S. 1372–1381.
H.-M. Polka: Experimentelle Bestimmung und Berechnung von Dampf-Flüssig-Gleichgewichten für Systeme mit starken Elektrolyten. Doktorarbeit. Univ. Oldenburg, 1993, S. 1–144.
Y. Gaston-Bonhomme, P. Petrino, J. L. Chevalier: UNIFAC-VISCO Group Contribution Method for Predicting Kinematic Viscosity: Extension and Temperature Dependence. In: Chem.Eng.Sci. 49(11), 1994, S. 1799–1806.
T. Holderbaum: Die Vorausberechnung von Dampf-Flüssig-Gleichgewichten mit einer Gruppenbeitragszustandsgleichung. In: Fortschrittsber. VDI Reihe 3, 243, 1991, S. 1–154.
H. E. Gonzàlez, J. Abildskov, R. Gani, P. Rousseaux, B. Le Bert: A method for prediction of UNIFAC group interaction parameters. In: AIChE J. 53, 2007, S. 1620–1633.
Y. Zhang, X. Zhang, W. Zhang, H. Qu, W. Wang: Prediction of Solid-Liquid Equilibrium to Synthetic Nitro-Musk by using UNIFAC Group-Contribution Method. In: Huaxue-gongcheng. 33(5), 2005, S. 69–71.
P. Ulbig: Gruppenbeitragsmodelle UNIVAP & EBGCM. Entwicklung der Gruppenbeitragsmodelle UNIVAP und EBGCM zur Vorhersage thermodynamischer Größen sowie Bestimmung der Modellparameter unter Verwendung evolutionärer Algorithmen. Hannemann-Verlag, 1996, ISBN 3-920088-70-0.

Weblinks

Commons: UNIFAC – Sammlung von Bildern, Videos und Audiodateien

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] A. Fredenslund, R. L. Jones, J. M. Prausnitz: Group-Contribution Estimation of Activity Coefficients in Nonideal Liquid Mixtures. In: AIChE J. 21(6), 1975, S. 1086–1099.

[2] Å. Fredenslund, J. Gmehling, P. Rasmussen: Vapor-Liquid Equilibria Using UNIFAC - A Group Contribution Method. Elsevier, Amsterdam 1977.

[3] A. Bondi: van der Waals Volumes and Radii. In: J.Phys.Chem. 68(3), 1964, S. 441–451.

[4] R. Wittig, J. Lohmann, J. Gmehling: Vapor-Liquid Equilibria by UNIFAC Group Contribution. 6. Revision and Extension. In: Ind.Eng.Chem.Res. 42(1), 2003, S. 183–188.

[5] J. Gmehling, B. Kolbe: Thermodynamik. 2. Auflage. VCH-Verlag, Weinheim 1992.

[6] J. Vidal: Thermodynamique. Méthodes appliquées au raffinage et au Génie Chimique. Editions Technip, 1997.

[7] Gudrun Wienke: Messung und Vorausberechnung von n-Octanol/Wasser-Verteilungskoeffizienten. Doktorarbeit. Univ. Oldenburg, 1993, S. 1–172.

[8] U. Weidlich, J. Gmehling: A Modified UNIFAC Model. 1. Prediction of VLE, hE, and γ^∞. In: Ind.Eng.Chem.Res. 26(7), 1987, S. 1372–1381.

[9] H.-M. Polka: Experimentelle Bestimmung und Berechnung von Dampf-Flüssig-Gleichgewichten für Systeme mit starken Elektrolyten. Doktorarbeit. Univ. Oldenburg, 1993, S. 1–144.

[10] Y. Gaston-Bonhomme, P. Petrino, J. L. Chevalier: UNIFAC-VISCO Group Contribution Method for Predicting Kinematic Viscosity: Extension and Temperature Dependence. In: Chem.Eng.Sci. 49(11), 1994, S. 1799–1806.

[11] T. Holderbaum: Die Vorausberechnung von Dampf-Flüssig-Gleichgewichten mit einer Gruppenbeitragszustandsgleichung. In: Fortschrittsber. VDI Reihe 3, 243, 1991, S. 1–154.

[12] H. E. Gonzàlez, J. Abildskov, R. Gani, P. Rousseaux, B. Le Bert: A method for prediction of UNIFAC group interaction parameters. In: AIChE J. 53, 2007, S. 1620–1633.

[13] Y. Zhang, X. Zhang, W. Zhang, H. Qu, W. Wang: Prediction of Solid-Liquid Equilibrium to Synthetic Nitro-Musk by using UNIFAC Group-Contribution Method. In: Huaxue-gongcheng. 33(5), 2005, S. 69–71.

[14] P. Ulbig: Gruppenbeitragsmodelle UNIVAP & EBGCM. Entwicklung der Gruppenbeitragsmodelle UNIVAP und EBGCM zur Vorhersage thermodynamischer Größen sowie Bestimmung der Modellparameter unter Verwendung evolutionärer Algorithmen. Hannemann-Verlag, 1996, ISBN 3-920088-70-0.