Simplex-Verfahren

Ein Simplex-Verfahren (auch Simplex-Algorithmus) ist ein Optimierungsverfahren der Numerik zur Lösung linearer Optimierungsprobleme, auch als Lineare Programme (LP) bezeichnet. Es löst ein solches Problem nach endlich vielen Schritten exakt oder stellt dessen Unlösbarkeit oder Unbeschränktheit fest. Die Grundidee der Simplex-Verfahren wurde 1947 von George Dantzig vorgestellt; seitdem haben sie sich durch zahlreiche Verbesserungen zu den wichtigsten Lösungsverfahren der linearen Optimierung in der Praxis entwickelt. Simplex-Verfahren sind Pivotverfahren.

Das Primalsimplex-Verfahren läuft von einer Ecke eines LP-Polyeders zur nächsten, bis keine Verbesserung mehr möglich ist

Obwohl bisher für jede Variante des Verfahrens ein Beispiel konstruiert werden konnte, bei dem der Algorithmus exponentielle Laufzeit benötigt, läuft ein Simplex-Algorithmus in der Praxis meist schneller als andere Verfahren, obwohl es zur Lösung einzelner linearer Programme auch andere konkurrenzfähige Methoden gibt, wie z. B. Innere-Punkte-Verfahren. Der große Vorteil eines Simplex-Algorithmus liegt jedoch darin, dass er bei leichter Veränderung des Problems – beispielsweise dem Hinzufügen einer zusätzlichen Bedingung – einen „Warmstart“ von der letzten verwendeten Lösung durchführen kann und daher meist nur wenige Iterationen zur erneuten Lösung benötigt, während andere Verfahren von vorne beginnen müssen. Darüber hinaus nutzt ein Simplex-Verfahren die engen Zusammenhänge zwischen einer linearen Optimierungsaufgabe und seiner dualen Aufgabe aus und löst grundsätzlich beide Probleme gleichzeitig. Beide Eigenschaften sind in der ganzzahligen linearen oder auch nichtlinearen Optimierung dort von Bedeutung, wo sehr viele ähnliche lineare Aufgaben in Folge gelöst werden müssen.

Die geometrische Grundidee des Algorithmus besteht darin, von einer beliebigen Ecke eines Polytops, das durch die lineare Optimierungsaufgabe definiert wird, entlang seiner Kanten zu einer optimalen Ecke zu laufen. Der Name des Verfahrens rührt daher, dass die nichtnegativen Linearkombinationen der Basisspalten in jeder Iteration einen simplizialen Kegel beschreiben. Ein Namensvetter dieses Verfahrens namens Downhill-Simplex-Verfahren (Nelder und Mead 1965[1]) basiert ebenfalls auf einem Simplex, ist aber ein iteratives Verfahren zur nichtlinearen Optimierung.

Geschichte

Die Grundlagen der linearen Optimierung wurden 1939 von dem russischen Mathematiker Leonid Witaljewitsch Kantorowitsch in seinem Buch „Mathematische Methoden in der Organisation und Planung der Produktion“ gelegt. Kurz danach (1941) präsentierte der US-Amerikaner Frank L. Hitchcock (1875–1957) eine Arbeit zu einem Transportproblem. Im Jahre 1947 veröffentlichte George Dantzig das Simplex-Verfahren, mit dem lineare Programme erstmals systematisch gelöst werden konnten. Eine der ersten dokumentierten Anwendungen der neuen Methode war das Diäten-Problem von George Stigler, dessen Ziel eine möglichst kostengünstige Nahrungszusammensetzung für Soldaten war, die bestimmte Mindest- und Höchstmengen an Vitaminen und anderen Inhaltsstoffen erfüllte. An der optimalen Lösung dieses linearen Programms mit neun Ungleichungen und 77 Variablen waren damals neun Personen beschäftigt, die zusammen etwa 120 Manntage Rechenarbeit benötigten.[2] Interesse an dieser Arbeit zeigte zunächst das amerikanische Militär, speziell die US Air Force, die militärische Einsätze optimieren wollte. In den Folgejahren entwickelten John von Neumann und Oskar Morgenstern das Verfahren weiter.

Mit dem Aufkommen von Computern Mitte der 1950er Jahre konnten auch größere Probleme gelöst werden. Es wurden spezielle Varianten der Simplexmethode entwickelt, wie das revidierte Simplex-Verfahren, das sehr sparsam mit dem damals knappen und teuren Hauptspeicher umging. Im Jahre 1954 brachte William Orchard-Hays die erste kommerzielle Implementierung dieses Verfahrens auf den Markt. Im selben Jahr veröffentlichten Carlton Lemke und E. M. L. Beale das duale Simplex-Verfahren, das sich heute – nach weiteren Verbesserungen – zu einer der Standardmethoden zur Lösung linearer Programme entwickelt hat.

Die theoretische Komplexität des Simplex-Verfahrens war lange Zeit unklar. Erst im Jahre 1972 konstruierten Victor Klee und George Minty ein Beispiel, bei dem der Algorithmus alle exponentiell vielen Ecken eines Polyeders abläuft, und zeigten damit die exponentielle Laufzeit des Verfahrens. Ähnliche Beispiele wurden bisher für alle bekannten Varianten des Verfahrens gefunden.

Ab den 1970er Jahren profitierte der Simplex-Algorithmus – wie auch andere Verfahren der Linearen Optimierung – von algorithmischen Fortschritten der numerischen linearen Algebra, insbesondere bei der Lösung großer linearer Gleichungssysteme. Vor allem die Entwicklung numerisch stabiler LR-Zerlegungen für dünnbesetzte Matrizen trug maßgeblich zum Erfolg und der Verbreitung des Simplex-Verfahrens bei.

Seit Mitte der 1970er bis Anfang der 1990er Jahre wurde das Verfahren durch die Entwicklung neuer Pivotstrategien deutlich verbessert. Vor allem die wachsende Bedeutung der ganzzahligen linearen Optimierung in den 1980er Jahren sowie die Entwicklung des dual steepest edge pricing in der Implementierung von J. J. Forrest und Donald Goldfarb (1992) machten das duale Simplex-Verfahren zum ernsthaften Konkurrenten für andere Lösungsmethoden. Umgekehrt hatte diese Verbesserung des dualen Simplex-Algorithmus einen maßgeblichen Anteil am Erfolg von Schnittebenenverfahren und Branch-and-Cut zur Lösung ganzzahliger linearer Programme. Darüber hinaus sorgten neue Preprocessing-Methoden in den 1990er Jahren dafür, dass immer größere LPs gelöst werden konnten. Unter der – in praktischen Anwendungen fast immer erfüllten – Voraussetzung, dass die auftretenden LP-Matrizen dünnbesetzt sind, können heute lineare Programme mit mehreren hunderttausend Variablen oder Ungleichungen innerhalb weniger Stunden optimal gelöst werden.

Grundidee

Die Simplex-Verfahren dienen zur Lösung linearer Optimierungsaufgaben, das ist die Suche nach reellen Variablenwerten, die ein System linearer Ungleichungen und Gleichungen erfüllen und dabei eine lineare Zielfunktion maximieren oder minimieren. Ausgegangen wird dabei von der Form

(LP)

\max _{x\in \mathbb {R} ^{n}}\left\{c^{T}x\mid \;Ax\leq b,\;x\geq 0\right\}\,,

wobei $A\in \mathbb {R} ^{m\times n}$ eine Matrix mit reellen Einträgen ist, $c\in \mathbb {R} ^{n}$ der sogenannte Zielfunktionsvektor, und $b\in \mathbb {R} ^{m}\!,~b\geq 0$ ein Spaltenvektor mit nichtnegativen Einträgen $b_{i}\geq 0$ . Ziel ist es, einen Punkt $x$ zu finden, der das lineare Ungleichungssystem erfüllt und einen möglichst hohen Zielfunktionswert $F(x)=c^{T}x$ hat.

Jedes lineare Programm kann durch einfache Umformungen in die Form

(LP)

\max _{x\in \mathbb {R} ^{n}}\left\{c^{T}x\mid \;Ax\leq b,\;x\geq 0\right\}

gebracht werden, bei welcher die Vorzeichen in $b\in \mathbb {R} ^{m}$ freilich immer noch beliebig sind. Das geschieht wie folgt:

Ein Minimierungsproblem kann durch Multiplikation der Zielfunktion mit $(-1)$ in ein Maximierungsproblem verwandelt werden.
Ungleichungen $\textstyle {\sum _{j}A_{ij}x_{j}\geq b_{i}}$ können als $\textstyle {\sum _{j}(-A_{ij})x_{j}\leq -b_{i}}$ geschrieben werden.
Vorhandene Gleichungsgruppen $\forall i~~\textstyle {\sum _{j}A_{ij}x_{j}=b_{i}}$ können in Ungleichungsgruppen $\forall i~~\textstyle {\sum _{j}A_{ij}x_{j}\leq b_{i}}$ mit $\textstyle {\sum _{j}{\big (}-\sum _{i}A_{ij}{\big )}x_{j}\leq -b_{i}}$ aufgespalten werden.
Variablengruppen $x_{j}$ mit beliebigem Wertebereich können über eine zusätzliche Variable und $x_{j}=u_{j}-w$ durch nichtnegative Variablen $\forall j~~u_{j}\geq 0,~~w\geq 0$ ersetzt werden.

Im Gegensatz zu diesen Umformungen ist die immer vorausgesetzte Startbedingung $b\geq 0$ nur über die Lösung einer Hilfsaufgabe in einer sogenannten "Phase 1" zu erreichen; dabei ist diese Hilfsaufgabe grundsätzlich ebenso aufwendig wie die eigentliche Optimierung.

Geometrisch lässt sich die Menge der zulässigen Lösungen, also die Menge der Punkte mit nichtnegativen Koordinaten, die das lineare Ungleichungssystem $Ax\leq b$ erfüllen, als konvexes Polyeder (mehrdimensionales Vieleck) $P$ interpretieren, dessen Dimension durch die Anzahl der Variablen nach oben begrenzt ist. Ziel ist es, einen Punkt $x$ in $P$ mit möglichst hohem Zielfunktionswert $F(x)=c^{T}x$ zu finden. Anschaulich entspricht dies der Verschiebung der Hyperebene $c^{T}x=0$ so weit wie möglich in Richtung des Vektors $c$ , so dass sie gerade noch das Polyeder berührt. Alle Berührungspunkte sind dann optimal.

Für die Menge der zulässigen Lösungen gibt es drei Möglichkeiten:

das LP besitzt keine zulässigen Lösungen, d. h., das Polyeder ist leer (z. B. $\max\{x\;|\;x\leq 1,\;x\geq 2\ \}$ ).
das LP ist unbeschränkt, d. h., es gibt Lösungen mit beliebig hohem Zielfunktionswert (z. B. $\max\{x\;|\;x\geq 0\}$ ).
es gibt genau eine oder unendlich viele Optimallösungen, die dann alle auf einer gemeinsamen Seitenfläche (Ecke, Kante, …) des Polyeders $P$ liegen.

Man kann zeigen, dass es immer eine optimale Ecke gibt, falls das Optimierungsproblem überhaupt zulässige Lösungen besitzt und beschränkt ist. Man kann sich also bei der Suche nach Optimallösungen auf die Ecken des Polyeders beschränken, von denen es allerdings sehr viele geben kann.

Die anschauliche Grundidee des Simplex-Verfahrens besteht nun darin, sich schrittweise von einer Ecke des Polyeders zu einer benachbarten Ecke mit besserem Zielfunktionswert zu hangeln, bis es keinen besseren Nachbarn mehr gibt. Da es sich bei der linearen Optimierung um ein konvexes Optimierungsproblem handelt, ist die so gefundene lokal optimale Ecke dann auch global optimal, d. h., es gibt in ganz $P$ keine andere Ecke mit besserem Zielfunktionswert mehr.

Laufzeit

Die Zahl der Ecken eines Polyeders kann exponentiell in der Anzahl der Variablen und Ungleichungen sein. Beispielsweise lässt sich der $n$ -dimensionale Einheitswürfel durch $2n$ lineare Ungleichungen beschreiben, besitzt aber $2^{n}$ Ecken. Klee und Minty konstruierten im Jahre 1972 einen verzerrten Einheitswürfel, den sogenannten Klee-Minty-Würfel, bei dem die von Dantzig vorgestellte Variante des Simplex-Verfahrens tatsächlich alle diese Ecken besuchte.[3] Ähnliche Beispiele wurden bisher für alle Zeilen- und Spaltenauswahlregeln gefunden. Dies bedeutet, dass der Simplex-Algorithmus in allen bisher bekannten Varianten im schlechtesten Fall exponentielle Laufzeit besitzt.

Bei degenerierten linearen Programmen, wie sie in der Praxis häufig auftreten, kann es zu sogenannten Zyklen kommen, bei dem das Simplex-Verfahren immer wieder dieselbe Ecke betrachtet und dadurch nicht terminiert. Dies lässt sich aber durch Anwendung der lexikographischen Zeilenauswahlregel oder durch absichtliche numerische Störungen verhindern.

Aus theoretischer Sicht ist das Simplex-Verfahren daher beispielsweise den Innere-Punkte-Verfahren mit polynomialer Laufzeit unterlegen. Aus praktischer Sicht hat es sich aber in vielen Fällen als schneller erwiesen. Der größte Vorteil des Simplex-Algorithmus gegenüber anderen Verfahren liegt jedoch darin, dass es bei kleinen Änderungen der Eingabedaten im Laufe des Algorithmus einen „Warmstart“ erlaubt, also die letzte berechnete Basis als Ausgangspunkt für wenige weitere (primale oder duale) Iterationen nehmen kann, während beispielsweise Innere-Punkte-Verfahren in solch einem Fall von vorne anfangen müssen. Dieser Fall tritt sehr häufig auf, wenn sehr viele ähnliche lineare Programme in Folge gelöst werden müssen, beispielsweise im Rahmen von Schnittebenenverfahren, Branch-and-Bound oder Branch-and-Cut.

In der Praxis hängt die Laufzeit des Simplex-Verfahren oft im Wesentlichen linear von der Anzahl der Zeilen ab. Tatsächlich zeigten Borgwardt und andere in den 1980er Jahren, dass solche Fälle wie der Klee-Minty-Würfel extrem selten sind und dass einige Varianten des Simplex-Algorithmus unter bestimmten Annahmen an den Input im Mittel nur polynomiale Laufzeit benötigen. Es ist aber bis heute unklar, ob es eine Variante mit polynomialer Laufzeit für alle Instanzen gibt.

Mathematische Beschreibung

Das Simplex-Verfahren setzt sich aus zwei Phasen zusammen:

Phase I bestimmt eine zulässige Startlösung oder stellt fest, dass das Problem keine Lösung besitzt,
Phase II verbessert eine bestehende Lösung immer weiter, bis keine Verbesserung der Zielfunktion mehr möglich ist oder die Unbeschränktheit des Problems festgestellt wird.

Die Big-M-Methode bietet eine Möglichkeit, beide Phasen zu verbinden, sprich den Simplex anzuwenden, auch wenn zunächst keine zulässige Startlösung gegeben ist.

Bestimmung einer Startlösung (Phase I)

Zunächst muss eine zulässige Startlösung berechnet werden, bevor man die Phase II starten kann. Eine Möglichkeit dafür ist, für jede Zeile $i$ eine künstliche Variable $z_{i}$ einzuführen und dann folgendes lineare Programm zu betrachten:

(LP1)

\min \left\{\left.\sum _{i=1}^{m}z_{i}\;\right|\;Ax+z=b,\;x,z_{1},\cdots ,z_{m}\geq 0\right\}~.

In einer Optimallösung dieses Hilfsproblems sind die künstlichen Variablen so klein wie möglich, wobei sie immer nichtnegativ bleiben müssen. Das ursprüngliche Problem (LP) besitzt genau dann eine zulässige Lösung, wenn es eine Lösung des Hilfsproblems mit $z=0$ gibt, bei der also keine künstlichen Variablen verwendet werden.

Das Hilfsproblem (LP1) besitzt für $b\geq 0$ eine einfache zulässige Startlösung, nämlich $(x,z)=(0,b)$ . Darüber hinaus gilt für jede zulässige Lösung des Hilfsproblems $z\leq b$ , so dass die Zielfunktion nach oben durch $\textstyle \sum _{i=1}^{m}b_{i}$ beschränkt ist. Dieses lineare Programm besitzt also eine Optimallösung, die ausgehend von der Startlösung $(0,b)$ mit Phase II des Hilfsproblems bestimmt werden kann. Findet man dabei eine Optimallösung $(x^{*},z^{*})$ mit $z^{*}=0$ , ist $x^{*}$ offensichtlich eine zulässige Startlösung für das Ausgangsproblem (LP), mit der dessen Phase II gestartet werden kann. Gelingt dies nicht, so ist das Ausgangsproblem nicht lösbar und man kann aufhören.

Bestimmung einer Optimallösung (Phase II)

Phase II ist ein iteratives Verfahren, das in jedem Schritt versucht, aus einer zulässigen Lösung eine neue Lösung mit besserem Zielfunktionswert zu konstruieren, bis dies nicht mehr möglich ist. Dies entspricht im Wesentlichen der wiederholten Lösung eines linearen Gleichungssystems mit Hilfe des Gaußschen Eliminationsverfahrens. Dabei kann auch evtl. die Unbeschränktheit des Optimierungsproblems festgestellt werden. Zur Erklärung dieser Phase ist die Definition einiger Begriffe notwendig.

Basen, Basislösungen und Ecken

In der Phase II des Simplex-Verfahrens spielt der Begriff der Basis eine wesentliche Rolle. Eine Basis $B$ von $A$ ist eine Teilmenge der Spalten von $A$ , die eine reguläre Untermatrix $A_{B}$ bilden. $B$ wird dabei als Indexvektor über die Spalten von $A$ dargestellt. Die Variablen, die zu den Basisspalten gehören, also in $B$ enthalten sind, heißen Basisvariablen, die anderen Nichtbasisvariablen. Die Basislösung zu einer gegebenen Basis $B$ ist der eindeutige Vektor $x$ , dessen Basisvariablen sich als $A_{B}^{-1}b$ ergeben und dessen Nichtbasisvariablen alle den Wert 0 haben (also $A_{B}\cdot x_{B}=b$ und $x_{N}=0$ ). Solch eine Basislösung ist also eine zulässige Lösung des Gleichungssystems $Ax=b$ mit höchstens $m$ Nicht-Null-Einträgen. In dem Fall, dass alle Komponenten von $x_{B}$ nichtnegativ sind, ist $x\geq 0$ auch eine zulässige Lösung von (LP), also ein Punkt des Polyeders $P$ .

Man kann zeigen, dass jede zulässige Basislösung einer Ecke (Extremalpunkt) des Polyeders entspricht und umgekehrt. Eine Basislösung heißt nicht degeneriert (nicht entartet), wenn sie genau $m$ Nicht-Null-Basiseinträge besitzt, also $x_{B}>0$ gilt. In diesem Fall gibt es eine eindeutige zugehörige Basis. Sind alle Basislösungen nicht degeneriert, gibt es also eine bijektive Abbildung zwischen Basen der Matrix $A$ und Ecken des Polyeders $P$ .

Ist eine Basislösung dagegen degeneriert, so hat sie weniger als $m$ Nicht-Null-Einträge und kann zu mehreren Basen gehören. In diesem Fall definiert also jede Basis der Matrix $A$ genau eine Ecke des Polyeders $P$ , aber nicht umgekehrt. Dieser Fall tritt auf, wenn eine Ecke von mehr als $n$ Ungleichungen definiert wird, was bei praktischen Planungsproblemen so gut wie immer der Fall ist.

Iterative Simplexschritte

Die Phase II versucht iterativ in jedem Austauschschritt, aus einer bestehenden Basislösung, wie sie z. B. in Phase I bestimmt wurde, eine neue Basislösung mit mindestens genauso gutem Zielfunktionswert zu konstruieren, indem sie eine Basisvariable aus der Basis entfernt und dafür eine bisherige Nichtbasisvariable in die Basis aufnimmt. Dies wird so lange wiederholt, bis kein verbessernder Austausch mehr möglich ist.

In dieser Phase gibt es zu Beginn jeder Iteration ein sogenanntes Simplextableau zur aktuellen Basis $B$ , in dem die Berechnungen durchgeführt werden. Es entspricht im Wesentlichen dem linearen Gleichungssystem $[A\;I\,]\,x=b\,$ , $[c^{T}\;0]\,x=z$ , nach einer Basistransformation in die aktuelle Basis.

Simplextableau

Für die Formulierung des Simplextableaus gibt es unterschiedliche Möglichkeiten; die hier vorgestellte Version basiert auf einem Vorlesungsskript[4] von Martin Grötschel. Jeder Simplexschritt geht von einer zulässigen Basis $B$ aus. Zu Beginn des Schrittes hat das zugehörige Simplextableau die folgende Form:

\left[\left.{\begin{matrix}{\bar {A}}&I&0\\{\bar {c}}&0&1\end{matrix}}\;\right|\;{\begin{matrix}{\bar {b}}\\{\bar {f}}\end{matrix}}\;\right]

Hierbei sind zur Vereinfachung der Darstellung die Spalten so umsortiert worden, dass alle Nichtbasisspalten links stehen und alle Basisspalten rechts. $I$ ist die $(m\!\times \!m)$ -dimensionale Einheitsmatrix. Die $(m\!\times \!n)$ -dimensionale Matrix ${\bar {A}}$ und die restlichen obigen Einträge sind definiert durch

{\bar {A}}=A_{B}^{-1}A_{N}

{\bar {b}}=A_{B}^{-1}b

{\bar {c}}=c_{N}^{T}-c_{B}^{T}A_{B}^{-1}A_{N}

{\bar {f}}=c_{B}^{T}A_{B}^{-1}b

Dabei ist

$A_{B}$ die reguläre Untermatrix von $A$ , die aus den Spalten der aktuellen Basis $B$ besteht,
$A_{N}$ die (meistens nicht quadratische) Untermatrix von $A$ , die aus den Nichtbasisspalten besteht,
$c_{B}$ die Teile des Zielfunktionsvektors $c$ , die aus den Basisspalten bestehen, und
$c_{N}$ die Teile des Zielfunktionsvektors $c$ , die aus den Nichtbasisspalten bestehen.

Die rechte Seite ${\bar {b}}$ enthält die Werte der Basisvariablen von der zu $B$ gehörenden Basislösung; ${\bar {f}}$ ist der Zielfunktionswert dieser Basislösung. Zu Beginn der Phase I bilden die Variablen $z_{i}$ eine zulässige Basis mit der Einheitsmatrix als Basismatrix und der zugehörigen Basislösung $(x,z)=(0,b)$ . Daher steht am Anfang auf der rechten Seite einfach der Vektor $b$ .

Die Einträge des Vektors ${\bar {c}}$ heißen reduzierte Kosten der Nichtbasisvariablen. Der Wert ${\bar {c}}_{j}$ gibt die Verbesserung der Zielfunktion an, wenn Variable $x_{j}$ um eine Einheit erhöht wird. Sind zu Beginn eines Simplexschrittes alle reduzierten Kostenkoeffizienten negativ oder 0, sind daher die aktuelle Basis und die zugehörige Basislösung optimal, da die Aufnahme einer bisherigen Nichtbasisvariable in die Basis den Zielfunktionswert verschlechtern würde. Gibt es dagegen Nichtbasisvariablen mit positiven reduzierten Kosten, wird im nächsten Simplexschritt eine von ihnen in die Basis aufgenommen und dafür eine andere Variable aus der Basis entfernt. Wenn die neue Variable innerhalb der Nebenbedingungen $Ax=b$ erhöht werden kann, verbessert sich der Zielfunktionswert.

Ein einzelner Simplexschritt

Für den eigentlichen Simplexschritt wählt man nun eine Spalte $s$ der einzufügenden Nichtbasisvariable und eine Zeile $r$ der aus der Basis zu entfernenden Basisvariablen. Seien ${\bar {a}}_{ij}$ die (Matrix-)Elemente des aktuellen Simplextableaus. Dann heißt ${\bar {a}}_{rs}$ das Pivotelement des Simplextableaus. Die Spalte $s$ heißt Pivotspalte, die Zeile $r$ heißt Pivotzeile. Ein Austauschschritt entspricht exakt einem Schritt beim Lösen eines linearen Gleichungssystems, bei dem man die Pivotzeile $r$ nach der Variablen $x_{s}$ auflöst und dann $x_{s}$ in die restlichen Gleichungen einsetzt. Bei einem Austauschschritt berechnet sich das neue Simplextableau folgendermaßen:

Pivotelement:

(1)

\qquad \;{\bar {a}}_{rs}:={\frac {1}{{\bar {a}}_{rs}}}

Pivotzeile für $j$ ungleich $s$ :

(2)

\qquad \;{\bar {a}}_{rj}:={\frac {{\bar {a}}_{rj}}{{\bar {a}}_{rs}}}

(3)

\qquad \;{\bar {b}}_{r}\;:={\frac {{\bar {b}}_{r}}{{\bar {a}}_{rs}}}

Pivotspalte für $i$ ungleich $r$ :

(4a)

\qquad {\bar {a}}_{is}:=-{\frac {{\bar {a}}_{is}}{{\bar {a}}_{rs}}}

(4b)

\qquad {\bar {c}}_{s}\;:=-{\frac {{\bar {c}}_{s}}{{\bar {a}}_{rs}}}

Restliche Elemente der Matrix und reduzierte Kosten:

(5a)

\qquad {\bar {a}}_{ij}:={\bar {a}}_{ij}-{\frac {{\bar {a}}_{is}{\bar {a}}_{rj}}{{\bar {a}}_{rs}}}

(5b)

\qquad {\bar {c}}_{j}\;:={\bar {c}}_{j}-{\frac {{\bar {c}}_{s}{\bar {a}}_{rj}}{{\bar {a}}_{rs}}}

Rechte Seite:

(6)

\qquad \;{\bar {b}}_{i}\;:={\bar {b}}_{i}-{\frac {{\bar {b}}_{r}{\bar {a}}_{is}}{{\bar {a}}_{rs}}}

Diese Rechenschritte entsprechen der Anwendung des Gaußschen Eliminationsverfahrens, um die Pivotspalte s im Tableau in einen Einheitsvektor zu transformieren. Dadurch wird die inverse Matrix $A_{B'}^{-1}$ zur neuen Basis $B'$ nicht komplett neu berechnet, sondern durch Modifikation der alten Basisinversen $A_{B}^{-1}$ konstruiert.

Ein Simplexschritt, der von einer nicht degenerierten Basislösung ausgeht, führt auf jeden Fall zu einer neuen Basislösung und damit auch zu einer neuen Ecke des Polyeders mit besserem Zielfunktionswert. Ist dagegen die Basislösung degeneriert, kann es passieren, dass die neue Basis nach dem Simplexschritt zur selben Basislösung und damit auch zur selben Ecke gehört, so dass der Zielfunktionswert sich nicht ändert. Bei unvorsichtiger Wahl der Pivotelemente kann es zu sogenannten Zyklen kommen, bei der reihum immer wieder dieselben Basen besucht werden, so dass der Algorithmus in eine Endlosschleife läuft. Dies lässt sich aber beispielsweise durch eine geeignete Auswahl der Pivotzeile verhindern. In der Praxis ist eine weitere Methode, mit Zykeln umzugehen, eine absichtliche Perturbation (numerische Störung) der Daten, die nach einigen Iterationen wieder rausgerechnet wird, wenn der Algorithmus die betreffende Ecke verlassen hat.

Für die Wahl des Pivotelements gibt es meist mehrere Möglichkeiten. Die ursprünglich von Dantzig vorgeschlagene Methode wählt eine der Spalten mit dem größten reduzierten Kostenwert und eine beliebige Zeile, bei der nach dem Simplexschritt wieder eine zulässige (insbesondere nichtnegative) Basislösung entsteht. Dazu muss bei gegebener Pivotspalte $s$ eine Pivotzeile gewählt werden, bei der das Minimum

{\displaystyle \lambda

angenommen wird. Sind alle Einträge in Spalte $s$ negativ, ist das Optimierungsproblem unbeschränkt, da man Lösungen mit beliebig gutem Zielfunktionswert konstruieren könnte. In diesem Fall kann man aufhören.

Im Normalfall gibt es sowohl mehrere Spalten mit positiven reduzierten Kosten als auch mehrere Zeilen, bei denen das Minimum $\lambda$ angenommen wird, so dass eine Wahlmöglichkeit besteht. Da die Wahl des Pivotelements einen großen Einfluss auf die Rechenzeit haben kann, sind innerhalb der letzten 60 Jahre zahlreiche verbesserte Pivotstrategien gegenüber der Lehrbuchvariante entwickelt worden (siehe unten).

Beispielrechnung

Veranschaulichung des Beispiels (Erklärung siehe Text)

Anhand eines einfachen Beispiels zur Produktionsplanung mit zwei Variablen soll der Lösungsweg Schritt für Schritt gezeigt werden. In diesem einfachen Fall ist eine Optimallösung leicht zu finden. Reale Probleme können dagegen leicht aus mehreren Hunderttausend Variablen und Nebenbedingungen bestehen, so dass man ihnen meistens die Existenz einer Lösung oder den Wert einer Optimallösung nicht unmittelbar ansehen kann.

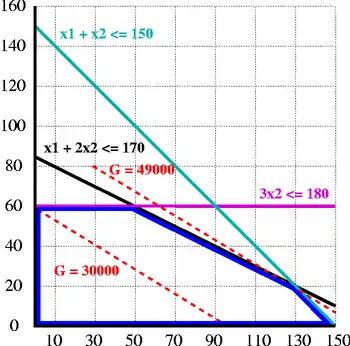
Eine Firma stellt zwei verschiedene Produkte her. Es stehen drei Maschinen A, B, C zur Verfügung. Maschine A hat eine maximale monatliche Laufzeit (Kapazität) von 170 Stunden, Maschine B von 150 Stunden und Maschine C von 180 Stunden. Eine Mengeneinheit (ME) von Produkt 1 liefert einen Deckungsbeitrag von 300 Euro, eine ME von Produkt 2 dagegen 500 Euro. Fertigt man 1 ME von Produkt 1, benötigt man dafür 1 Stunde die Maschine A und zusätzlich 1 Stunde die Maschine B. 1 ME von Produkt 2 belegt sowohl 2 Stunden Maschine A, als auch 1 Stunde Maschine B und 3 Stunden Maschine C.

Daraus erhält man folgende Bedingungen:

{\begin{matrix}1\cdot x_{1}&+&2\cdot x_{2}&\leq &170&{\mbox{(Maschine A)}}\\[2pt]1\cdot x_{1}&+&1\cdot x_{2}&\leq &150&{\mbox{(Maschine B)}}\\[2pt]0\cdot x_{1}&+&3\cdot x_{2}&\leq &180&{\mbox{(Maschine C)}}\\[2pt]\end{matrix}}

x_{1}\geq 0,\ x_{2}\geq 0

Die Firma möchte den Deckungsbeitrag $z\,$ maximieren:

\max \;z=300\cdot x_{1}+500\cdot x_{2}

$z\,$ ist daher der sogenannte Zielfunktionswert.

Eventuelle Fixkosten sind unabhängig von der Produktionsmenge und können daher einfach am Ende der Berechnung vom Gesamtdeckungsbeitrag abgezogen werden, um den Gewinn zu erhalten.

Überführung in Gleichungen

Für das Simplex-Verfahren werden die Ungleichungen zunächst in Gleichungen überführt. Dazu führt man so genannte Schlupfvariablen $y_{A}\,$ , $y_{B}\,$ und $y_{C}\,$ ein, welche die nicht genutzten Zeiten der einzelnen Maschinen darstellen. Offensichtlich dürfen die Schlupfvariablen nicht negativ sein. Damit lässt sich das Problem so formulieren, dass man die Schlupfvariablen bezüglich der ursprünglichen Variablen freilegt. Ein derart genormtes Gleichungssystem heißt im Englischen dictionary (Benennung von V. Chvátal):

Maximiere die Zielfunktion $z\,$ unter den Nebenbedingungen:

{\begin{matrix}z&=&~~~~~~0&+~300\,x_{1}&+~500\,x_{2}\\[3pt]y_{A}&=&~~~170&-~~~~1\,x_{1}&-~~~~2\,x_{2}\\[2pt]y_{B}&=&~~~150&-~~~~1\,x_{1}&-~~~~1\,x_{2}\\[2pt]y_{C}&=&~~~180&+~~~~0\,x_{1}&-~~~~3\,x_{2}\end{matrix}}

x_{1}\geq 0,\ x_{2}\geq 0

y_{A}\geq 0,\ y_{B}\geq 0,\ y_{C}\geq 0

Die obigen Gleichungen kann man in das vorher beschriebene Simplex-Tableau übertragen:

      -----------------------------
      |  x₁     x₂   | rechte Seite
  ---------------------------------
  -z  |  300   500  |      0
  ---------------------------------
  y_A  |   1      2   |      170  = b₁
  y_B  |   1      1   |      150  = b₂
  y_C  |   0      3   |      180  = b₃

In der Kopfzeile stehen die Nichtbasisvariablen $x_{1},\,x_{2}$ mit dem Wert 0, während die Basisvariablen $y_{i}\,$ in der ersten Spalte stehen. In der obersten Zeile – der Gleichung für die Zielfunktion – stehen die Zielfunktionskoeffizienten $c_{i}\,$ , also 300 und 500. Auf der rechten Seite steht die aktuelle Basislösung, was in diesem Fall genau $b\,$ ist. In der obersten Zeile der rechten Seite steht das Negative des Zielfunktionswertes für die aktuelle Basislösung, im Beispiel also das Negative des Gesamtdeckungsbeitrags. Dieser ist momentan 0, da nichts produziert wird.

Bestimmung einer zulässigen Ausgangslösung (Phase I)

Da die konstanten Größen des obigen Gleichungssystems nicht negativ sind, kann man die unabhängigen Variablen des Gleichungssystems (Nichtbasisvariablen) auf Null setzen und so eine triviale zulässige Lösung angeben, mit der direkt die Phase II gestartet werden kann:

x_{1}=0,\ x_{2}=0\qquad y_{A}=170,\ y_{B}=150,\ y_{C}=180

Die Variablen $y_{i}\,$ bilden eine zulässige Basis $B\,$ , deren Basismatrix $A_{B}\,$ die Einheitsmatrix ist. Die zugehörige Basislösung ist also $A_{B}^{-1}b=b$ . Diese Lösung entspricht dem Fall, dass nichts produziert wird ( $x_{i}=0\,$ ). Die Restkapazität der Maschinen, die durch die Werte der $y_{i}\,$ angegeben wird, ist hier deren Gesamtkapazität (170, 150 und 180), da die Maschinen nicht genutzt werden.

Verbesserung der Ausgangslösung (Phase II)

Da die soeben berechnete Ausgangslösung unbefriedigend ist, wird nun in Phase II versucht, bessere zulässige Lösungen zu finden.

Auswahl einer Pivotspalte und -zeile

In einer Simplex-Iteration wird eine Basisvariable gegen eine der unabhängigen Variablen ausgetauscht. In Frage kommen Nichtbasisvariablen mit positivem Zielfunktionskoeffizienten, da deren Aufnahme in die Basis den Zielfunktionswert verbessern kann. Diese Variable soll soweit erhöht werden, bis eine oder mehrere der Basisvariablen auf 0 stoßen. Eine beliebige dieser Basisvariablen verlässt dann die Basis und wird gegen die Nichtbasisvariable ausgetauscht.

Variable $x_{1}\,$ hat den positiven Zielfunktionskoeffizienten 300; indem sie erhöht wird, lässt sich die Zielfunktion $z\,$ vergrößern; sie kommt also als basis-eintretende Pivotvariable in Frage. Solange $x_{1}\,$ die einzige erhöhte Nichtbasisvariable ist, soll diese Erhöhung ${\bar {x}}_{1}\,$ durch folgende Bedingungen eingeschränkt werden:

{\begin{matrix}0\leq {\bar {y}}_{A}=170-1\,{\bar {x}}_{1}&\quad {\text{(zu Basisvariable }}y_{A}{\text{)}}\\[2pt]0\leq {\bar {y}}_{B}=150-1\,{\bar {x}}_{1}&\quad {\text{(zu Basisvariable }}y_{B}{\text{)}}\\[2pt]\end{matrix}}

In anderen Worten,

{\bar {x}}_{1}\leq {\frac {170}{1}},\quad {\bar {x}}_{1}\leq {\frac {150}{1}}

oder

{\bar {x}}_{1}\leq \min {\Bigl \{}{\frac {170}{1}},\ {\frac {150}{1}}{\Bigr \}}=\min\{170,150\}=150

Die erste der Basisvariablen, die in diesem Fall auf Null stößt, erhält man über den Quotienten $150/1\,$ und ist $y_{B}\,$ . Diese ist die Variable, die gegebenenfalls gegen $x_{1}\,$ ausgetauscht werden müsste. Der neue Wert der Zielfunktion wäre dann ${\bar {z}}=300\cdot (150/1)=45000$ .

Auch Variable $x_{2}\,$ hat mit 500 einen positiven Zielfunktionskoeffizienten, kommt also ebenfalls als eintretende Nichtbasisvariable in Frage. Nach der obigen Vorgehensweise erhalten wir

{\begin{matrix}0\leq {\bar {y}}_{A}=170-2\,{\bar {x}}_{2}&\quad {\text{(zu Basisvariable }}y_{A}{\text{)}}\\[2pt]0\leq {\bar {y}}_{B}=150-1\,{\bar {x}}_{2}&\quad {\text{(zu Basisvariable }}y_{B}{\text{)}}\\[2pt]0\leq {\bar {y}}_{C}=180-3\,{\bar {x}}_{2}&\quad {\text{(zu Basisvariable }}y_{C}{\text{)}}\\[2pt]\end{matrix}}

und somit

{\bar {x}}_{2}\leq \min {\Bigl \{}{\frac {170}{2}},\ {\frac {150}{1}},\ {\frac {180}{3}}{\Bigr \}}=\min\{85,150,60\}=60

Der minimale Quotient $(180/3)\,$ gehört zur Basisvariable $y_{C}\,$ . Der neue Wert der Zielfunktion wäre ${\bar {z}}=500\cdot (180/3)=30000$ .

Für den Zuwachs der Zielfunktion in diesem Schritt ist es also am günstigsten, den ersten Fall zu wählen und die unabhängige Variable $x_{1}\,$ anstelle der Basisvariablen $y_{B}\,$ freizulegen.

Durchführung eines Austauschschrittes

Mit dem Austauschschritt wird die Basisvariable $y_{B}\,$ gegen die Nichtbasisvariable $x_{1}\,$ ausgetauscht. Zuerst legen wir in der Gleichung für $y_{B}\,$ die unabhängige Unbekannte $x_{1}\,$ frei,

{\begin{matrix}y_{B}~=~150-1\,x_{1}-1\,x_{2}\qquad \qquad \qquad \qquad \qquad \\[3pt]\Longrightarrow \quad x_{1}~=~150-1\,y_{B}-1\,x_{2}\end{matrix}}

und anschließend ersetzen wir $x_{1}\,$ in den restlichen Gleichungen für den so erhaltenen Ausdruck:

{\begin{matrix}z&~=~&~~~~0&+~300\,(150-1\,y_{B}-1\,x_{2})&+~500\,x_{2}\\[2pt]y_{A}&~=~&~170&-~~~~1\,(150-1\,y_{B}-1\,x_{2})&-~~~~2\,x_{2}\\[2pt]y_{C}&~=~&~180&+~~~~0\,(150-1\,y_{B}-1\,x_{2})&-~~~~3\,x_{2}\end{matrix}}

Das führt zu den oben beschriebenen Verwandlungsregeln für das Simplex-Tableau nach dem Pivotelement $a_{21}=1$ . Wenn $x_{1}\,$ die Zeile von $y_{B}\,$ besetzt und $y_{B}\,$ die Spalte von $x_{1}\,$ , dann ist das neue Gleichungssystem

{\begin{matrix}z&=&45000&-~300\,y_{B}&+~200\,x_{2}\\[2pt]y_{A}&=&~~~~20&+~~~~1\,y_{B}&-~~~~1\,x_{2}\\[2pt]x_{1}&=&~~~150&-~~~~1\,y_{B}&-~~~~1\,x_{2}\\[2pt]y_{C}&=&~~~180&+~~~~0\,y_{B}&-~~~~3\,x_{2}\end{matrix}}

Die Unbekannte $x_{1}\,$ ist in die Basis gerückt, die jetzt unabhängige Unbekannte $y_{B}\,$ ist eine Nichtbasisvariable und erscheint in der Kopfzeile.

Diese Lösung bedeutet: Es werden $150\,$ ME von Produkt 1 (Gleichung mit freigelegtem $x_{1}\,$ ) produziert. Von Produkt 2 wird nichts gefertigt ( $x_{2}=0\,$ ist Nichtbasisvariable). Damit erzielt die Firma einen Gesamtdeckungsbeitrag von 45.000 Euro. Maschine A steht $20\,$ Stunden pro Monat still (sie läuft nur 150 der 170 möglichen Stunden). Maschine B hat keine Leerlaufzeit. Maschine C steht $180\,$ Stunden still, das heißt, sie wird überhaupt nicht benötigt. Dies ergibt sich auch direkt aus der Aufgabenstellung: Maschine C wird nur bei der Herstellung von Produkt 2 benötigt. Da dieses nicht gefertigt wird, braucht man Maschine C noch nicht.

Das zum obigen Gleichungssystem gehörende neue Simplex-Tableau ist

      -----------------------------
      |  y_B     x₂   | rechte Seite
  ---------------------------------
  -z  |  -300   200  |      -45000
  ---------------------------------
  y_A  |  -1      1   |       20  = b₁
  x₁  |   1      1   |      150  = b₂
  y_C  |   0      3   |      180  = b₃

Die Einträge des neuen Simplex-Tableaus können anhand der oben angeführten Formeln errechnet werden.

Wiederholung der Simplexschritte

Da die Zielfunktion im entstandenen Simplex-Tableau noch einen positiven Koeffizienten enthält, kann man die Lösung noch verbessern. Dies geschieht mittels einer weiteren Simplex-Iteration. Bei der Auswahl des Pivotelementes kommt nur die Unbekannte $x_{2}\,$ in Frage, da nur hier der Zielfunktionskoeffizient positiv ist. Die Basisvariable des Pivots ergibt sich aus

{\begin{matrix}0\leq {\bar {y}}_{A}=~20-1\,{\bar {x}}_{2}&\quad {\text{(zu Basisvariable }}y_{A}{\text{)}}\\[2pt]0\leq {\bar {x}}_{1}=150-1\,{\bar {x}}_{2}&\quad {\text{(zu Basisvariable }}x_{1}{\text{)}}\\[2pt]0\leq {\bar {y}}_{C}=180-3\,{\bar {x}}_{2}&\quad {\text{(zu Basisvariable }}y_{C}{\text{)}}\\[2pt]\end{matrix}}

und somit

{\bar {x}}_{2}\leq \min \left\{{\frac {20}{1}},\ {\frac {150}{1}},\ {\frac {180}{3}}\right\}=\min\{20,150,60\}=20

Damit ist Zeile $y_{A}\,$ die einzige Basisunbekannte, die für einen Pivot in Frage kommt. Die Basisvariable $y_{A}\,$ wird gegen die Nichtbasisvariable $x_{2}\,$ ausgetauscht; das Pivotelement ist $1\,$ . Mit den gleichen Umrechnungen wie oben erhält man als neues Gleichungssystem

{\begin{matrix}z&=&49000&-~100\,y_{B}&-~200\,y_{A}\\[2pt]x_{2}&=&~~~~20&+~~~~1\,y_{B}&-~~~~1\,y_{A}\\[2pt]x_{1}&=&~~~130&-~~~~2\,y_{B}&+~~~~1\,y_{A}\\[2pt]y_{C}&=&~~~120&-~~~~3\,y_{B}&+~~~~3\,y_{A}\end{matrix}}

beziehungsweise ein neues Simplex-Tableau

      -----------------------------
      |  y_B     y_A   | rechte Seite
  ---------------------------------
  -z  | -100   -200  |   -49000
  ---------------------------------
  x₂  |  -1      1   |       20
  x₁  |   2     -1   |      130
  y_C  |   3     -3   |      120

Da die Zielfunktion nun keine positiven Koeffizienten mehr enthält, ist eine optimale Lösung erreicht. Es werden $130\,$ ME von Produkt 1 und $20\,$ ME von Produkt 2 hergestellt. Damit erzielt die Firma einen Gesamtdeckungsbeitrag von 49.000 Euro. Maschine A und Maschine B sind voll ausgelastet. Maschine C läuft 60 Stunden und hat daher noch eine ungenutzte Kapazität von $y_{C}=120\,$ Stunden.

Einträge in Bruchzahlform

Das obige Beispiel wurde in algebraischer Notation gelöst, indem man im Gleichungssystem die Basisvariablen bezüglich der restlichen, unabhängigen Variablen freilegt. Um Rundungsfehler zu vermeiden, kann man mit Bruchzahlen arbeiten und einen gemeinsamen Nenner für das gesamte Gleichungssystem wählen (dass dieser Nenner oben immer $1\,$ war, ist Zufall). Um in jedem Schritt den gemeinsamen Nenner für das Gesamtsystem zu finden, müssen wir die Einträge nicht zusätzlich analysieren. Falls das Startsystem ganzzahlig ist (was sich normalerweise durch Erweiterung erreichen lässt), gilt die Regel:

Der Zähler des gewählten Pivotelements ist ein gemeinsamer Nenner für das darauffolgende System

Wenn wir die neuen Tableau-Einträge mit diesem gemeinsamen Nenner multiplizieren, erhalten wir stets ganzzahlige Zähler. Bei der Berechnung dieser Zähler für die neuen Tableau-Einträge wird dann ungeprüft durch den alten Nenner geteilt, wobei das Ergebnis ganzzahlig sein muss.

Als Beispiel für diese Vorgehensweise lösen wir dieselbe Aufgabe wie oben noch einmal mit Dantzigs Pivotauswahl; hierbei wird als eingehende Pivotvariable diejenige mit größtem Zielfunktionskoeffizienten gewählt:

{\begin{matrix}z&=&(&~~~~~~~0&+~300\,x_{1}&+~500\,x_{2}&)~/~1\\[2pt]y_{A}&=&(&~~~~170&-~~~~~\,x_{1}&-~~~~2\,x_{2}&)~/~1\\[2pt]y_{B}&=&(&~~~~150&-~~~~~\,x_{1}&-~~~~~\,x_{2}&)~/~1\\[2pt]y_{C}&=&(&~~~~180&+~~~~0\,x_{1}&-~~~~\mathbf {3\,x_{2}} &)~/~1\end{matrix}}

Durch Erhöhung der unabhängigen Variable $x_{2}\,$ lässt sich die Zielfunktion $z\,$ vergrößern; die erste der Basisvariablen, die in diesem Fall auf Null stößt, ist $y_{C}\,$ . Folglich kann man $x_{2}\,$ anstelle von $y_{C}\,$ freilegen und erhält folgendes System mit ${\bar {z}}=30000$ :

{\begin{matrix}z&=&(&~90000&+~900\,x_{1}&-~500\,y_{C}&)~/~3\\[2pt]y_{A}&=&(&~~~~150&-~~~~\mathbf {3\,x_{1}} &+~~~~2\,y_{C}&)~/~3\\[2pt]y_{B}&=&(&~~~~270&-~~~~3\,x_{1}&+~~~~~\,y_{C}&)~/~3\\[2pt]x_{2}&=&(&~~~~180&+~~~~0\,x_{1}&-~~~~~\,y_{C}&)~/~3\end{matrix}}

Wenn man die unabhängige Variable $x_{1}\,$ erhöht, vergrößert man die Zielfunktion; die erste der Basisvariablen, die dann auf Null stößt, ist $y_{A}\,$ . Folglich legt man $x_{1}\,$ anstelle von $y_{A}\,$ frei und erhält folgendes System mit ${\bar {z}}=45000$ :

{\begin{matrix}z&=&(&135000&-~900\,y_{A}&+~100\,y_{C}&)~/~3\\[2pt]x_{1}&=&(&~~~~150&-~~~~3\,y_{A}&+~~~~2\,y_{C}&)~/~3\\[2pt]y_{B}&=&(&~~~~120&+~~~~3\,y_{A}&-~~~~~\mathbf {\,y_{C}} &)~/~3\\[2pt]x_{2}&=&(&~~~~180&+~~~~0\,y_{A}&-~~~~~\,y_{C}&)~/~3\end{matrix}}

Wenn man die unabhängige Variable $y_{C}\,$ erhöht, vergrößert man die Zielfunktion; die erste der Basisvariablen, die dann auf Null stößt, ist $y_{B}\,$ . Folglich legt man ${y_{C}\,}$ anstelle von $y_{B}\,$ frei und erhält folgendes System mit ${\bar {z}}=49000$ :

{\begin{matrix}z&=&(&~49000&-~200\,y_{A}&-~100\,y_{B}&)~/~1\\[2pt]x_{1}&=&(&~~~~130&+~~~~~\,y_{A}&-~~~~2\,y_{B}&)~/~1\\[2pt]y_{C}&=&(&~~~~120&+~~~~3\,y_{A}&-~~~~3\,y_{B}&)~/~1\\[2pt]x_{2}&=&(&~~~~~20&-~~~~~\,y_{A}&+~~~~~\,y_{B}&)~/~1\end{matrix}}

Die Zielfunktion hat Wert ${\bar {z}}=49000\,$ und lässt sich nicht mehr erhöhen; die Lösung ist wie oben ${\bar {x}}_{1}=130,\,{\bar {x}}_{2}=20$ . Wir beobachten nebenher, dass Dantzigs Pivotauswahl im Vergleich zur anfangs gewählten Alternative einen Schritt mehr gebraucht hat, um zur Lösung zu gelangen.

Beispielhafte Lösung in Java

Das Simplex-Verfahren steht bereits als Software-Implementierung in zahlreichen Software-Bibliotheken zur Verfügung. Ein Beispiel ist z. B. das Java-Package org.apache.commons.math3.optim von Apache Commons™. Die zu maximierende Funktion wird als LinearObjectiveFunction (Zeile 22) definiert und entspricht dem Deckungsbeitrag aus dem obigen Beispiel. Die Bedingungen werden als LinearConstraint (Zeilen 24–26) angegeben. Der SimplexSolver (Zeile 28) benötigt zur Lösung die Anzahl an maximalen Iterationen, die zu maximierende Funktion, die Bedingungen und die Information, ob ein Maximum bzw. Minimum gesucht wird (Zeile 29). Zusätzlich erhält der SimplexSolver mit dem NonNegativeConstraint die Information, dass für die Koordinaten $x_{1},x_{2}$ Werte größer 0 gesucht werden.

package SimplexAlgorithmExample;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collection;

import org.apache.commons.math3.optim.MaxIter;
import org.apache.commons.math3.optim.PointValuePair;
import org.apache.commons.math3.optim.linear.LinearConstraint;
import org.apache.commons.math3.optim.linear.LinearConstraintSet;
import org.apache.commons.math3.optim.linear.LinearObjectiveFunction;
import org.apache.commons.math3.optim.linear.NonNegativeConstraint;
import org.apache.commons.math3.optim.linear.Relationship;
import org.apache.commons.math3.optim.linear.SimplexSolver;
import org.apache.commons.math3.optim.nonlinear.scalar.GoalType;


public class SimplexAlgorithmExample
{
    public static void main(String[] args)
    {
        LinearObjectiveFunction oFunc = new LinearObjectiveFunction(new double[] {300, 500}, 0);
        Collection<LinearConstraint> constraints = new ArrayList<LinearConstraint>();
        constraints.add(new LinearConstraint(new double[] {1, 2}, Relationship.LEQ, 170));
        constraints.add(new LinearConstraint(new double[] {1, 1}, Relationship.LEQ, 150));
        constraints.add(new LinearConstraint(new double[] {0, 3}, Relationship.LEQ, 180));

        SimplexSolver solver = new SimplexSolver();
        PointValuePair solution = solver.optimize(new MaxIter(100), oFunc, new LinearConstraintSet(constraints), GoalType.MAXIMIZE, new NonNegativeConstraint(true));
        System.out.println(Arrays.toString(solution.getPoint()) + " : " + solution.getSecond());
    }
}

Duale Information im Tableau

Aus dem Simplextableau lässt sich auch die Information zur Lösung des zu dem linearen Programm (LP) gehörigen dualen linearen Programms entnehmen. Zu einer gegebenen Basis $B$ kann man neben der zugehörigen Primallösung $x={\bar {b}}=A_{B}^{-1}b$ , die in der rechten Spalte des Tableaus steht, auch eine Duallösung $\pi ^{T}=c_{B}^{T}A_{B}^{-1}$ berechnen. Diese beiden Vektoren $x$ und $\pi$ erfüllen immer die Bedingung

\pi ^{T}b=c^{T}x

,

die für Optimallösungen notwendig ist. Der Vektor $x$ bleibt nach Konstruktion der einzelnen Simplexiterationen immer zulässig für das primale LP, während der Vektor $\pi$ Bedingungen des dualen LPs verletzen kann. Sind zu einer Basis sowohl die zugehörige Primallösung $x$ als auch die entsprechende Duallösung $\pi$ zulässig (man spricht dann von einer primal und dual zulässigen Basis), dann sind beide optimal für das primale bzw. duale lineare Programm. Man kann zeigen, dass dies genau dann der Fall ist, wenn der reduzierte Kostenvektor ${\bar {c}}$ nichtpositiv ist. Obwohl das Ziel des Simplex-Verfahrens eigentlich nur die Berechnung einer optimalen Primallösung ist, fällt also am Ende auch eine optimale Duallösung nebenbei mit ab.

Eine Beispielrechnung zur Dualität befindet sich im Artikel Pivotverfahren.

Varianten und Verbesserungen

In der hier vorgestellten Form, die im Wesentlichen der ursprünglichen Version von Dantzig entspricht, wird der Simplex-Algorithmus in praktischen Implementierungen heute nicht mehr verwendet. Im Laufe der Zeit sind einige Varianten des Simplex-Verfahrens entwickelt worden, die die Rechenzeit und den Speicherbedarf beim Lösen linearer Programme gegenüber dem Standardverfahren deutlich verkürzen und numerisch deutlich stabiler sind. Die wichtigsten Verbesserungen, die heute zum Standard in guten LP-Lösern gehören, sollen hier kurz vorgestellt werden.

Auswahl des Pivotelementes

Bei der Auswahl des Pivotelements hat man in der Regel einige Freiheiten. Die Pivotspalte $s$ und die Pivotzeile $r$ können beliebig gewählt werden, unter den Bedingungen, dass

die Pivotspalte positive reduzierte Kosten hat und
die Pivotzeile wieder zu einer zulässigen Basislösung führt.

Die Wahl des Pivotelementes hat oft großen Einfluss auf die Anzahl der Iterationen und auf die numerische Stabilität des Verfahrens, insbesondere bei degenerierten Problemen. Die Entwicklung besserer Pivotstrategien, insbesondere zur Spaltenauswahl, haben im Laufe der Zeit große Fortschritte bei der Beschleunigung des Lösungsprozesses bewirkt.

Spaltenauswahl

Für die Auswahl der Pivotspalte (engl. pricing) gibt es verschiedene Strategien, die unterschiedlichen Rechenaufwand erfordern und je nach Eingabedaten unterschiedlich gut funktionieren:[5][6]

Wähle die erste geeignete Spalte. Dies ist die einfachste Variante, die aber oft zu sehr vielen Iterationen führt und daher in der Praxis nicht verwendet wird.
Die ursprünglich von Dantzig vorgeschlagene Methode wählt eine der Spalten mit dem größten reduzierten Kostenwert. Diese Variante kann bei vielen Variablen viel Rechenzeit beanspruchen.
Das steepest-edge pricing ist eine Kombination aus Spalten- und Zeilenwahl, die zusammen den größten Fortschritt für die Zielfunktion bringen. Diese Variante ist in jeder Iteration sehr aufwändig, führt aber oft zu wenigen Iterationen.
Das devex pricing ist eine 1974 von Paula Harris vorgeschlagene Approximation von steepest-edge pricing und eines der Standardverfahren in heutigen LP-Lösern. Hierbei werden die Spalten der Matrix und die reduzierten Kosten vor der Auswahl auf eine einheitliche Norm skaliert, um die Aussagekraft der reduzierten Kosten zu erhöhen.
Beim partial pricing wird die Variablenmenge in Blöcke unterteilt und eines der obigen vorherigen Verfahren auf einen Block angewendet. Erst wenn dort keine geeignete Variable gefunden wird, wird überhaupt der nächste Block betrachtet.
Das multiple pricing sucht einmal eine Menge von geeigneten Variablen heraus, die dann in den nächsten Iterationen bevorzugt als Kandidaten betrachtet werden. Erst wenn keiner dieser Kandidaten mehr positive reduzierte Kosten besitzt, werden die anderen Variablen betrachtet.
Das partial multiple pricing ist eine Kombination der letzten beiden Varianten, die neue Kandidaten immer nur aus einem Teil aller zur Verfügung stehenden Variablen bestimmt. Diese Strategie gehört neben devex pricing heute zu den Standardstrategien.
Beim hybrid pricing werden mehrere Strategien je nach Situation abwechselnd verwendet. Einige LP-Löser wenden zusätzlich noch numerische Kriterien bei der Spaltenauswahl an, um die Probleme durch Rundungsfehler in Grenzen zu halten.
Die Regel von R. G. Bland[7] wählt zunächst die Spalte mit kleinstem Index unter allen in Frage kommenden Spalten. Das ist sinnvoll, wenn danach bei mehreren zur Auswahl stehenden Zeilen ebenfalls diejenige mit kleinstem Index gewählt wird. Ein Beweis, dass diese Regel Zyklen verhindert, ist zum Beispiel in[8] enthalten.

Zeilenauswahl

Gibt es mehrere geeignete Pivotzeilen, hat man die Wahl zwischen mehreren Varianten:

Wähle die erste geeignete Zeile. Diese Variante ist zwar pro Iteration sehr schnell, führt aber insgesamt oft zu vielen Iterationen und ist numerisch instabil.
Die lexikographische Auswahlregel wählt unter allen in Frage kommenden Zeilen die (eindeutige) lexikographisch kleinste Zeile aus. Diese Regel ist unter dem Gesichtspunkt der Geschwindigkeit nicht besonders gut, verhindert aber, dass Tableaus mehrfach besucht werden und der Algorithmus ins Zykeln gerät. Aus diesem Grund kann sie beispielsweise für einige Iterationen verwendet werden, um von einer Basislösung wegzukommen, bevor wieder auf andere Auswahlverfahren umgestellt wird.
Der 1973 von Paula Harris vorgeschlagene Harris-Quotiententest, der heute zu den Standardverfahren zählt, erlaubt aus Gründen der numerischen Stabilität eine leichte Unzulässigkeit der neuen Lösung.
Wähle unter den geeigneten Zeilen zufällig. Zyklen werden so sehr unwahrscheinlich, aber nicht unmöglich.

Variablenschranken

In der Praxis müssen häufig obere und untere Schranken für die Variablen berücksichtigt werden. Dies gilt insbesondere dann, wenn lineare Programme beispielsweise im Rahmen eines Branch-and-Cut-Prozesses als Unterproblem gelöst werden. Für solche einfachen Arten von Ungleichungen wie Variablenschranken gibt es das sogenannte Bounded-Simplex-Verfahren, bei dem die Schranken direkt in den einzelnen Simplex-Schritten berücksichtigt werden. Im Gegensatz zur Standardversion, bei dem eine Nichtbasisvariable immer den Wert 0 hat, kann sie jetzt auch den Wert einer ihrer Schranken annehmen. Diese Mitführung der Schranken in den einzelnen Schritten bewirkt eine kleinere Anzahl der Zeilen und damit eine kleinere Basis gegenüber der offensichtlichen Variante, Variablenschranken als Ungleichungen in das LP zu schreiben.

Duales Simplex-Verfahren

Neben einer optimalen Primallösung, also einer Lösung für das gegebene lineare Programm, berechnet das oben beschriebene primale Simplex-Verfahren auch eine optimale Duallösung, also eine Lösung des zugehörigen dualen linearen Programms. Da das duale LP aus dem primalen im Wesentlichen durch Vertauschung von Zeilen und Spalten entsteht, lässt sich mit dem Simplex-Verfahren auch das duale Problem lösen, indem man das gegenüber der obigen Variante leicht modifizierte Tucker-Tableau verwendet und im beschriebenen Algorithmus Zeilen und Spalten vertauscht. Diese Variante heißt dann duales Simplex-Verfahren. Es wurde erstmals 1954 von Carlton Lemke und E. M. L. Beale beschrieben, ist aber erst seit Anfang der 1990er Jahre fester Bestandteil kommerzieller LP-Löser, als erfolgreiche Pivotstrategien dafür entwickelt wurden, wie das dual steepest-edge pricing in der Version von Forrest und Goldfarb aus dem Jahre 1992.

In der Praxis hängt die Laufzeit des Simplex-Verfahrens oft im Wesentlichen von der Anzahl der Zeilen im LP ab. Dies gilt insbesondere für dünnbesetzte Matrizen, wie sie in der Praxis normalerweise auftreten. Wenn ein lineares Programm sehr viele Bedingungen, aber nur wenige Variablen hat, kann es sich daher lohnen, stattdessen das duale LP zu lösen, bei dem Zeilen- und Spaltenzahl vertauscht sind, und sich dabei eine optimale Primallösung mitliefern zu lassen, die nebenbei mitberechnet wird.

Ein weiterer großer Vorteil der primal-dualen Betrachtungsweise ist es, dass primale und duale Simplexschritte abwechselnd im selben Tableau durchgeführt werden können. Anstatt das Tableau explizit zu transponieren, werden einfach im Algorithmus Zeilen- und Spaltenoperationen vertauscht, je nachdem, ob gerade der primale oder der duale Algorithmus benutzt wird. Im Gegensatz zum primalen Simplex-Verfahren, das immer eine zulässige Primallösung behält und erst am Ende eine zulässige Duallösung erreicht, ist es beim dualen Simplex-Verfahren umgekehrt. Wenn also die Primallösung zu einer Basis unzulässig, die zugehörige Duallösung aber zulässig ist, kann man durch duale Simplexschritte versuchen, wieder zu einer primal zulässigen Lösung zu kommen. Dies kann man in mehreren Zusammenhängen ausnutzen, die hier kurz beschrieben werden sollen.

Im Verlauf von Schnittebenenverfahren oder Branch-and-Cut-Verfahren wird sehr oft in einem gerade gelösten LP eine Variablenschranke verändert oder eine Ungleichung hinzugefügt, die von der alten Lösung nicht erfüllt wird, und anschließend das LP neu gelöst. Da die alte Basislösung jetzt nicht mehr zulässig ist, ist eine der Grundbedingungen des primalen Simplextableaus verletzt, so dass das primale Simplexverfahren von vorne starten muss, um das neue LP zu lösen. Wenn an der Zielfunktion nichts verändert wurde, ist aber die alte Duallösung weiter zulässig, so dass mit einigen dualen Simplexschritten von der alten Startbasis aus meist nach wenigen Iterationen eine Optimallösung für das modifizierte LP gefunden wird. Dieser Unterschied schlägt sich bei großen LPs oft sehr deutlich in der Gesamtlaufzeit nieder.
Wenn im Verlauf des Algorithmus numerische Schwierigkeiten auftreten oder es sehr lange keinen Fortschritt in der Zielfunktion gibt, kann es sinnvoll sein, vorübergehend eine leichte Verletzung von Variablenschranken zu erlauben, um sich aus einer kritischen Ecke des Polytops hinauszubewegen. Dies kann anschließend mit einigen dualen Simplexschritten wieder behoben werden.
Wenn das lineare Programm bestimmte Strukturen aufweist, kann man direkt eine primal unzulässige, aber dual zulässige Startbasis angeben, ohne dafür rechnen zu müssen. In solch einem Fall kann man von dieser Basis aus direkt in Phase II mit dualen Simplexschritten starten und kann sich die Phase I sparen.

Revidiertes Simplex-Verfahren

Obwohl praktisch auftretende lineare Programme mehrere hunderttausend Variablen haben können, arbeitet das Simplex-Verfahren immer nur mit einem kleinen Teil davon, nämlich den Basisvariablen. Lediglich bei der Spaltenauswahl müssen die Nichtbasisspalten betrachtet werden, wobei es – je nach Pivotstrategie – oft ausreicht, nur einen Teil davon zu berücksichtigen. Diese Tatsache macht sich das revidierte Simplex-Verfahren zunutze, das immer nur die aktuelle Basismatrix $A_{B}$ oder deren Inverse speichert, zusammen mit etwas Zusatzinformationen, aus der die aktuelle Basismatrix bzw. deren Inverse berechnet werden kann. Dadurch kommt es mit wesentlich weniger Speicherplatz aus als das ursprüngliche Tableauverfahren. Dieses Verfahren bildet heute die Grundlage mehrerer guter LP-Löser.

In der ersten kommerziellen Implementierung dieses Verfahrens von William Orchard Hays im Jahre 1954 wurde die Basisinverse noch in jedem Schritt komplett neu berechnet, was mit den damaligen Lochkartenrechnern eine Herausforderung darstellte. Wenig später implementierte er die sogenannte Produktform der Inversen nach einer Idee von A. Orden. Dabei wurde nur die erste Basisinverse gespeichert, zusammen mit Update-Vektoren, aus denen die aktuelle Inverse in jedem Schritt berechnet werden konnte. Der damalige Rekord lag bei einem linearen Programm mit 71 Variablen und 26 Ungleichungen, das innerhalb von acht Stunden optimal gelöst wurde. In heute verwendeten Implementierungen wird eher die Basismatrix selbst mit Hilfe einer speziellen Form der LR-Zerlegung gespeichert, da die Inverse einer dünnbesetzten Matrix in der Regel nicht dünnbesetzt ist.

LR-Zerlegungen

Im Verlauf des Simplex-Verfahrens werden sehr viele ähnliche lineare Gleichungssysteme gelöst. Da große lineare Gleichungssysteme auch in anderen Zusammenhängen (beispielsweise bei der Lösung von Differentialgleichungen) häufig auftreten, wurden in den 1970er Jahren in der numerischen linearen Algebra Verfahren zur LR-Zerlegung einer Matrix entwickelt. Dabei wird die Matrix in eine untere und eine obere Dreiecksmatrix zerlegt, was es anschließend erlaubt, viele Gleichungssysteme mit derselben Matrix, aber unterschiedlichen rechten Seiten effizient zu lösen.

Im Falle des Simplex-Verfahrens wird diese Methode auf die Basismatrix $A_{B}$ angewandt. Da diese sich im Laufe des Simplex-Algorithmus ständig ändert, muss ihre LR-Zerlegung bei jedem Simplexschritt angepasst werden, beispielsweise mit Hilfe des nach seinen Erfindern benannten Forest-Tomlin-Updates. Diese Anpassung erfordert nur sehr geringen Aufwand im Vergleich zur Berechnung einer komplett neuen LR-Zerlegung, weil sich die Basismatrix in jeder Iteration nur in einer Spalte ändert. In praktischen Implementierungen wird meist aus numerischen Gründen trotzdem alle paar hundert Iterationen eine komplett neue LR-Zerlegung der aktuellen Matrix berechnet. Oft kann die Matrix schon durch geschickte Umsortierung der Zeilen und Spalten größtenteils in Dreiecksform gebracht werden, so dass nur noch ein kleiner Teil der Basismatrix, der sogenannte Nucleus, tatsächlich faktorisiert werden muss. Für die Berechnung der LR-Zerlegung selbst gibt es wieder verschiedene Varianten, von denen sich in der Praxis vor allem die LR-Zerlegung mit dynamischer Markowitz-Pivotisierung durchgesetzt hat, da diese die Dünnbesetztheit von Matrizen bei der Zerlegung weitgehend erhält. Dieses Verfahren hat vor allem für große lineare Programme, die fast immer dünnbesetzt sind, zu starken Reduktionen der Rechenzeit geführt.

Preprocessing

In den letzten zehn Jahren sind durch verbessertes Preprocessing sehr große Fortschritte in den Lösungszeiten erzielt worden. Beispielsweise gibt es oft numerische Probleme, wenn in einem linearen Gleichungssystem sowohl sehr große als auch sehr kleine Zahlen auftreten. In einigen Fällen lässt sich dies durch Vorkonditionierung, also z. B. Äquilibrierung des Gleichungssystems, vor dem Start des eigentlichen Algorithmus vermeiden.

Eine andere Klasse von Methoden des Preprocessing versucht, Redundanzen im linearen Gleichungssystem zu erkennen oder Variablenschranken zu verschärfen, um die Anzahl der Zeilen und Spalten zu reduzieren:

Wenn eine Zeile linear abhängig von anderen Zeilen ist, ist sie überflüssig und kann entfernt werden. Dies ist allerdings – bis auf den Spezialfall, dass eine Zeile ein skalares Vielfaches einer anderen Zeile ist – im Allgemeinen schwierig mit vertretbarem Aufwand zu erkennen.
Sehr oft sind Variablen aufgrund von Bedingungen auf einen bestimmten Wertebereich beschränkt oder durch andere Variablen festgelegt. Beispielsweise sind durch die Gleichung $x_{1}+x_{2}=1$ und die Nichtnegativitätsbedingungen beide Variablen auf den Bereich $[0,1]$ beschränkt. Die Kenntnis dieser Schranke kann den Lösungsprozess beschleunigen. Darüber hinaus ist der Wert von $x_{2}$ durch den Wert von $x_{1}$ festgelegt. Dadurch kann man in allen Bedingungen, in denen $x_{2}$ vorkommt, diese Variable durch $1-x_{1}$ ersetzen und $x_{2}$ aus dem linearen Programm entfernen.
Wenn mehrere Variablen auf einen bestimmten Wertebereich fixiert wurden, kann es sein, dass einige Ungleichungen immer erfüllt sind oder nicht mehr erfüllt werden können. Im ersten Fall kann die Ungleichung entfernt werden, im zweiten Fall ist sofort die Unzulässigkeit des linearen Programms gezeigt, und man kann aufhören.

Mit Hilfe solcher Methoden kann gerade bei sehr großen linearen Programmen die Anzahl der Zeilen und Spalten manchmal deutlich reduziert werden, was sich in sehr viel kürzeren Lösungszeiten widerspiegelt.

Literatur

George B. Dantzig: Lineare Programmierung und Erweiterungen. Springer-Verlag, 1966 (Originalausgabe: Linear Programming and Extensions, Princeton University Press, ISBN 0-691-05913-6).
V. Klee, G.J. Minty: How Good is the Simplex Algorithm? In: O. Shisha (editor): Inequalities III. Academic Press, New York 1972, S. 159–175.
Vašek Chvátal: Linear Programming. W. H. Freeman and Company, New York 1983, ISBN 0-7167-1587-2.
Alexander Schrijver: Theory of Linear and Integer Programming. John Wiley and Sons, 1998, ISBN 0-471-98232-6.
Wolfgang Domschke, Andreas Drexl: Einführung in Operations Research. 7. Auflage. Springer, Berlin 2007, ISBN 978-3-540-70948-0.
Michael Sauer: Operations Research kompakt 1. Auflage. Oldenbourg, München 2009, ISBN 978-3-486-59082-1.
Winfried Hochstättler: Algorithmische Mathematik. Springer, Berlin / Heidelberg 2010, ISBN 978-3-642-05421-1.

Weblinks

Hilfreiche OR-Zusammenfassung der TU Kaiserslautern
simplex me – the simple simplex solver. (Lineare Optimierungsprobleme mit Simplex-Algorithmus lösen – mehrsprachig, PDF Export)
Simplex Applet mit textueller Eingabe des Programms
Rechner Simplexalgorithmus zeigt alle Zwischenschritte mit Erläuterung
GNU Scientific Library enthält simplex code
nonlinear optimization (Memento vom 29. Dezember 2008 im Internet Archive)

Einzelnachweise

John A. Nelder, R. Mead: A simplex method for function minimization. In: Computer Journal. 7, 1965, S. 308–313. doi:10.1093/comjnl/7.4.308.
Robert Bixby: Solving real-world linear programs: A decade and more of progress. In: Operations Research, Band 50, Nr. 1, 2002, S. 3–15.
Harvey J. Greenberg: Klee-Minty Polytope Shows Exponential Time Complexity of Simplex Method. (PDF) University of Colorado at Denver, 1997.
Martin Grötschel: Algorithmische Diskrete Mathematik II: Lineare Optimierung, Vorlesungsskript (PDF; 947 kB).
István Maros: A General Pricing Scheme for the Simplex Method. (PDF) Technical Report 2001/3, Department of Computing, Imperial College, London 2001, ISSN 1469-4174.
Roland Wunderling: Paralleler und Objektorientierter Simplex-Algorithmus. (Memento vom 25. September 2006 im Internet Archive) Dissertation, TU Berlin, 1996.
R. Sedgewick: Algorithmen. Addison-Wesley Publishing Company, 1992, ISBN 3-89319-301-4, S. 697.
M. Padberg: Linear Optimization and Extensions. Springer, Berlin/Heidelberg 1995.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] John A. Nelder, R. Mead: A simplex method for function minimization. In: Computer Journal. 7, 1965, S. 308–313. doi:10.1093/comjnl/7.4.308.

[2] Robert Bixby: Solving real-world linear programs: A decade and more of progress. In: Operations Research, Band 50, Nr. 1, 2002, S. 3–15.

[3] Harvey J. Greenberg: Klee-Minty Polytope Shows Exponential Time Complexity of Simplex Method. (PDF) University of Colorado at Denver, 1997.

[4] Martin Grötschel: Algorithmische Diskrete Mathematik II: Lineare Optimierung, Vorlesungsskript (PDF; 947 kB).

[5] István Maros: A General Pricing Scheme for the Simplex Method. (PDF) Technical Report 2001/3, Department of Computing, Imperial College, London 2001, ISSN 1469-4174.

[6] Roland Wunderling: Paralleler und Objektorientierter Simplex-Algorithmus. (Memento vom 25. September 2006 im Internet Archive) Dissertation, TU Berlin, 1996.

[7] R. Sedgewick: Algorithmen. Addison-Wesley Publishing Company, 1992, ISBN 3-89319-301-4, S. 697.

[8] M. Padberg: Linear Optimization and Extensions. Springer, Berlin/Heidelberg 1995.