Ganzzahlige lineare Optimierung

Die ganzzahlige lineare Optimierung (auch ganzzahlige Optimierung) ist ein Teilgebiet der angewandten Mathematik. Wie die lineare Optimierung beschäftigt sie sich mit der Optimierung linearer Zielfunktionen über einer Menge, die durch lineare Gleichungen und Ungleichungen eingeschränkt ist. Der Unterschied liegt darin, dass in der ganzzahligen Optimierung einige oder alle Variablen nur ganzzahlige Werte annehmen dürfen und nicht beliebige reelle Werte wie in der linearen Optimierung. Die ganzzahlige Optimierung lässt sich geometrisch als Optimierung über einem konvexen Polyeder (einem höherdimensionalen Vieleck) auffassen und ist damit ein Spezialfall der konvexen Optimierung. Im Unterschied zur linearen Programmierung ist allerdings das zugrundeliegende Polyeder meist nicht genau bekannt, was das Problem aus komplexitätstheoretischer Sicht NP-schwer macht.

Da mindestens eine Variable diskret, also nicht kontinuierlich ist, ist auch der Begriff diskrete Optimierung gebräuchlich. Eine weitere häufige Bezeichnung ist ganzzahlige (lineare) Programmierung (von engl. integer (linear) programming), wobei der Begriff Programm im Sinne von Planung zu verstehen ist und nicht im Sinne eines Computerprogramms. Er wurde schon in den 1940er Jahren von George Dantzig geprägt, bevor Computer zur Lösung von Optimierungsproblemen eingesetzt wurden.

Noch stärker als die lineare hat sich die ganzzahlige Optimierung seit ihren Anfängen in den 1950er Jahren zu einem Modellierungs- und Optimierungswerkzeug für viele praktische Probleme entwickelt, für die keine speziellen Algorithmen bekannt sind. Durch bedeutende Fortschritte in der Entwicklung der Lösungsverfahren in den 1980er und 1990er Jahren hat die ganzzahlige Optimierung heute viele Anwendungen, beispielsweise in der Produktion, in der Planung von Telekommunikations- und Nahverkehrsnetzen und in der Tourenplanung.

Zur Lösung ganzzahliger Optimierungsprobleme gibt es einerseits exakte Lösungsverfahren wie beispielsweise Branch-and-Bound und Schnittebenenverfahren, die auf der Lösung vieler ähnlicher linearer Programme basieren, und andererseits eine Vielzahl von Heuristiken. Trotzdem ist die Lösung ganzzahliger linearer Programme in der Praxis immer noch eine schwere Aufgabe, die je nach Größe und Struktur des zu lösenden Problems eine geschickte Modellierung und mehr oder weniger speziell entwickelte oder angepasste Algorithmen erfordert. Oft werden daher mehrere Lösungsverfahren kombiniert.

Problemdefinition

Mathematische Formulierung

Ein ganzzahliges Programm (englisch integer program, IP) hat die gleiche Form wie ein lineares Programm (LP), mit dem Unterschied, dass die Variablen ganzzahlig sein müssen:

\max _{x\in \mathbb {Z} ^{n}}\left\{c^{T}x\;|\;Ax\leq b,x\geq 0\right\}

Dabei ist $A$ eine reelle Matrix und $b$ und $c$ sind Vektoren passender Dimension. Die Bedingung $Ax\leq b$ ist komponentenweise zu verstehen, also als

a_{i}\cdot x=\sum _{j=1}^{n}a_{ij}x_{j}\leq b_{i}

für alle Zeilen $i$ der Matrix $A$ . Genauso bedeutet die Bedingung $x\geq 0$ , dass alle Einträge des Vektors $x$ nichtnegativ sein müssen. Gelten die Ganzzahligkeitsbedingungen nur für einen Teil der Variablen, spricht man auch von einem gemischt-ganzzahligen Programm (engl. mixed-integer program, MIP). Auch die Präzisierung ganzzahliges lineares Programm (engl. integer linear program, ILP) ist gebräuchlich. Wie auch in der linearen Optimierung gibt es mehrere äquivalente Formulierungen, die sich ineinander transformieren lassen (siehe Lineare Optimierung: Problemdefinition).

Geometrische Interpretation

Die ganzzahlige Optimierung lässt sich, wie die lineare Variante, zu einem großen Teil geometrisch interpretieren. Die Menge

P:=\{x\in \mathbb {R} ^{n}\;|\;Ax\leq b,x\geq 0\},

die durch Weglassen der Ganzzahligkeitsbedingungen entsteht, bildet ein konvexes Polyeder im $n$ -dimensionalen Raum, dessen beschränkende Hyperebenen den Zeilen des Ungleichungssystems entsprechen. $P$ enthält u. a. alle zulässigen Punkte des Ausgangssystems, also alle ganzzahligen Punkte, die die Bedingungen $Ax\leq b$ erfüllen, aber im Unterschied zur linearen Optimierung sind nicht alle Punkte in $P$ zulässig. Das lineare Programm

\max \,\{c^{T}x\;|\;x\in P\}

wird als LP-Relaxierung des ganzzahligen Problems bezeichnet und spielt eine bedeutende Rolle für einige Lösungsverfahren (siehe unten).

Wie lineare Programme können auch ganzzahlige Programme unlösbar oder unbeschränkt sein. In allen anderen Fällen gibt es mindestens eine Optimallösung, sofern das Ungleichssystem nur rationale Einträge hat. Es ist im Gegensatz zur reellen linearen Optimierung möglich, Probleme zu konstruieren, die keine Optimallösung haben, obwohl Lösungen existieren und die Zielfunktion beschränkt ist. Im Unterschied zu LPs ist die Menge der Optimallösungen eines IPs keine Seitenfläche des Polyeders $P$ , so dass es neben genau einer oder unendlich vielen optimalen Lösungen auch eine andere endliche Anzahl (größer als 1) davon geben kann.

Beispiele

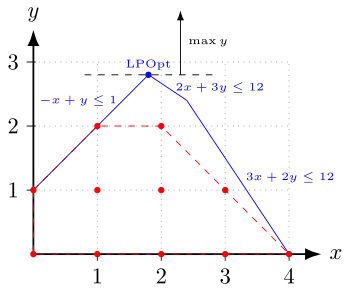
Polytop der zulässigen ganzzahligen Punkte (rot) mit LP-Relaxierung (blau)

Im nebenstehenden Bild ist das ganzzahlige lineare Programm

{\begin{matrix}\max &&y\\&-x&+y&\leq 1\\&3x&+2y&\leq 12\\&2x&+3y&\leq 12\\&&x,y\in \mathbb {Z} _{\geq 0}\end{matrix}}

dargestellt. Die zulässigen ganzzahligen Punkte sind rot eingezeichnet, und die rot gestrichelten Linien kennzeichnen ihre konvexe Hülle, also das kleinste Polyeder, das alle diese Punkte enthält. Über diesem Polyeder soll eigentlich optimiert werden, aber es ist meist nicht genau bekannt. Die blauen Linien zusammen mit den Koordinatenachsen begrenzen das Polyeder $P$ der LP-Relaxierung, das durch das Ungleichungssystem ohne Ganzzahligkeitsbedingungen gegeben ist. Ziel der Optimierung ist es, die schwarz gestrichelte Linie so weit parallel nach oben (in Richtung des Vektors $c=(0;1)$ ) zu verschieben, dass sie das jeweilige Polyeder gerade noch berührt. Die Optimallösungen des ganzzahligen Problems sind also die Punkte $(1;2)$ und $(2;2)$ mit dem Zielfunktionswert $c^{T}x=(0;1)^{T}(1;2)=(0;1)^{T}(2;2)=2$ . Die – in diesem Fall eindeutige – optimale Lösung der LP-Relaxierung mit dem Zielfunktionswert 2,8 ist der blau markierte Punkt $LP_{opt}=(1{,}8;2{,}8)$ , der nicht ganzzahlig und damit auch nicht zulässig für das IP ist.

Das folgende IP ist ein Beispiel für den oben erwähnten Spezialfall:

{\begin{matrix}\max &-{\sqrt {2}}x&+y\\&-{\sqrt {2}}x&+y&\leq 0\\&&x&\geq 1\\&&y&\geq 0\\&&x,y\in \mathbb {Z} \end{matrix}}

Die zulässigen Lösungen wie z. B. $(10;14)$ stellen rationale Approximationen für ${\sqrt {2}}$ in der Form ${\frac {y}{x}}$ dar. Da ${\sqrt {2}}$ irrational ist und daher beliebig genau approximiert werden kann, gibt es keine Optimallösung, obwohl die Zielfunktion durch die erste Bedingung nach oben beschränkt ist.

Anwendungen

Die Ganzzahligkeitsbedingungen erweitern die Modellierungsmöglichkeiten für praktische Probleme gegenüber der linearen Optimierung beträchtlich. Es gibt zwei Hauptgründe für ganzzahlige Variablen:

Die Variablen müssen aus praktischen Gründen ganzzahlig sein. Beispielsweise können nicht 3,7 Flugzeuge gebaut werden, sondern nur eine ganze Anzahl.
Die ganzzahligen Variablen sind auf die Werte 0 oder 1 beschränkt (sogenannte Binärvariablen) und repräsentieren Entscheidungen. Beispielsweise kann ein Bus nicht zu einem Drittel fahren, sondern nur entweder ganz oder gar nicht.

Oft treten auch beide Fälle zusammen auf. Die ganzzahlige Optimierung kann in vielen praktischen Anwendungsfeldern eingesetzt werden, von denen nachfolgend einige kurz beschrieben werden sollen.

Produktionsplanung

In der Produktionsplanung taucht oft das Problem auf, Produktionsmengen für mehrere Produkte zu bestimmen, die sich gemeinsame Ressourcen (Maschinen, Arbeitszeit, Lagerkapazitäten …) teilen. Ziel ist beispielsweise die Maximierung des gesamten Deckungsbeitrags, ohne die vorhandenen Ressourcen zu überschreiten. In einigen Fällen lässt sich dies mit Hilfe eines linearen Programms ausdrücken, aber oft müssen die Variablen aus praktischen Gründen ganzzahlig sein (s. o.).

Öffentlicher Nahverkehr

Bei der Dienst- und Umlaufplanung im öffentlichen Nahverkehr geht es darum, beispielsweise Busse oder U-Bahnen so auf die einzelnen Linien zu verteilen, dass der Fahrplan erfüllt werden kann, und sie mit Fahrern auszustatten. Hier spielen binäre Entscheidungsvariablen eine große Rolle, die z. B. ausdrücken, ob ein bestimmter Bustyp eine Linie befährt oder nicht, oder ob ein U-Bahn-Fahrer einem bestimmten Zug zugewiesen wird oder nicht.

Telekommunikationsnetze

Ziel der Kapazitäts- und Routing-Planung in landesweiten Telekommunikationsnetzen ist es, Kapazität auf den Knoten und Leitungen eines Netzes so zu installieren und Kommunikationsbedarfe darin so zu routen, dass alle Bedarfe erfüllt werden und die Gesamtkosten des Netzes minimal sind. Die Kapazität kann in der Regel nicht in beliebigen Anteilen installiert werden, sondern nur in bestimmten ganzzahligen Einheiten. Meist gibt es, abhängig von der verwendeten Technologie, noch weitere Beschränkungen, die sich als lineare Ungleichungen mit ganzzahligen oder binären Variablen modellieren lassen.

Mobilfunknetze

Die Aufgabe der Frequenzplanung in GSM-Mobilfunknetzen besteht darin, die verfügbaren Frequenzen so auf die Antennen zu verteilen, dass alle Nutzer bedient werden können und die störende Interferenz zwischen den Antennen minimiert wird. Dieses Problem lässt sich als ganzzahliges lineares Programm formulieren, bei dem u. a. Binärvariablen repräsentieren, ob eine Frequenz einer bestimmten Antenne zugewiesen wird oder nicht.

Tourenplanung

Die Tourenplanung, speziell das Problem des Handlungsreisenden, ist ein klassisches Beispiel der ganzzahligen Optimierung, dessen Untersuchung viel zur Entwicklung allgemeiner Lösungsverfahren beigetragen hat. Anschaulich geht es darum, eine kürzeste Rundreise zwischen einer gegebenen Menge von Städten zu finden. Dieses Problem kann als ganzzahliges lineares Programm mit exponentiell vielen Ungleichungen modelliert werden. Verschiedene erweiterte Varianten der Tourenplanung tauchen in der Praxis beispielsweise beim Bohren von Leiterplatten auf, oder auch bei der Planung der Fahrtrouten für Außendienstmitarbeiter (z. B. eines technischen Kundendienstes oder einer Versicherung), die alle ihre Kunden mit möglichst kurzen Wegen bedienen wollen.

0/1-Programmierung

Ein besonders wichtiger Spezialfall der ganzzahligen Optimierung ist die Optimierung, bei der die Variablen nicht nur ganzzahlige Werte annehmen dürfen, sondern auf die binären Werte 0 oder 1 beschränkt sind. Dadurch lässt sich die Suche nach Lösungen für Boolesche Funktionen in die Geometrie übertragen: Das Finden einer Belegung einer solchen Funktion wird äquivalent zum Finden von 0/1-Punkten in Schnitt und der Vereinigung von hochdimensionalen Polytopen. Diese Methode wird disjunktive Programmierung genannt und wurde Ende der 1960er Jahre von Egon Balas entwickelt. 0/1-Programmierung ist ein kombinatorisch schwieriges Problem und gehört zu Karps 21 NP-vollständigen Problemen.

Geschichte

Der Beginn der ganzzahligen Optimierung hängt eng mit der Entwicklung der linearen Optimierung Mitte der 1940er Jahre zusammen. Im Jahre 1947 veröffentlichte George Dantzig mehrere entscheidende Arbeiten zur linearen Optimierung und zum Simplex-Verfahren, die er in den darauffolgenden Jahren zusammen mit John von Neumann und anderen weiterentwickelte.

Als mit dem Aufkommen von Computern in den 1950er Jahren die ersten praktisch einsetzbaren Computerprogramme zur Lösung linearer Programme entwickelt wurden, rückte auch die Lösbarkeit ganzzahliger Optimierungsprobleme in erreichbare Nähe. Mitte der 1950er Jahre arbeiteten D. R. Fulkerson, G. Dantzig, und S. Johnson an ersten Schnittebenen für das Problem des Handlungsreisenden. Ohne Kenntnis dieser Arbeiten und motiviert durch ehemalige Kollegen der US Navy, die an ganzzahligen Lösungen interessiert waren, entwickelte Ralph Gomory im Jahre 1958 während seines Aufenthaltes in Princeton das erste allgemein einsetzbare Schnittebenenverfahren, das (zumindest theoretisch) die vollständige Lösbarkeit beliebiger ganzzahliger Programme erlaubte. Auch wenn sich dies praktisch nur teilweise umsetzen ließ, stellte dieses Verfahren einen entscheidenden algorithmischen Fortschritt dar.

Kurz danach, im Jahre 1960, stellten Ailsa Land und Alison Doig (später Alison Harcourt) das Branch-and-Bound-Verfahren vor, das auf einer geschickten Enumeration des Suchraumes basiert. 1965 gab R. J. Dakin einen einfach implementierbaren Algorithmus dazu an. Später wurde maßgeblich von Egon Balas Branch-and-Bound mit Schnittebenenverfahren zu Branch-and-Cut kombiniert, was die Lösung deutlich größerer ganzzahliger linearer Programme erlaubte.

Ende der 1960er Jahre entwickelte unter anderem Egon Balas eine allgemeine Methode, um lineare Beschreibungen zu finden, die von vorneherein nur ganzzahlige Ecken enthalten. Dieses sogenannte Lift-and-Project beruht auf der Idee, die Optimierung in einen hochdimensionalen Raum zu verlagern und die gefundene Lösung in niedrigere Dimensionen zu projizieren.

In den 1980er Jahren arbeiteten Manfred Padberg und andere an Schnittebenen für oft auftauchende Teilstrukturen wie Rucksackprobleme, die oft auch in allgemeinerem Kontext eingesetzt werden können. Die enormen algorithmischen Fortschritte in der linearen Optimierung in den 1990er Jahren schlugen sich auch in einer deutlich besseren Lösbarkeit ganzzahliger Programme nieder, da beispielsweise bei der Anwendung von Schnittebenenverfahren und Branch-and-Bound-Algorithmen sehr viele lineare Programme gelöst werden müssen. Neben besseren Modellierungen und Lösungstechniken für häufig auftauchende Teilprobleme, wie beispielsweise Netzwerkflüsse, wurden parallel dazu viele Heuristiken, also Näherungsverfahren, entwickelt, die meist in kurzer Zeit zulässige Lösungen berechnen. Sie können u. a. auch als Teil von Branch-and-Cut-Verfahren eingesetzt werden, um diese zu beschleunigen. All diese Verfahren sind noch Gegenstand aktueller Forschung.

Komplexität und Lösungsverfahren

Im Unterschied zu linearen Programmen, die beispielsweise mit Innere-Punkte-Verfahren in Polynomialzeit optimal gelöst werden können, ist das Finden einer beweisbaren Optimallösung für ganzzahlige Programme ein NP-schweres Problem. Dies macht sich auch in der Praxis bemerkbar. Während selbst große lineare Programme heute weitgehend mit Standardmethoden gelöst werden können, hängt die Lösbarkeit ganzzahliger Programme sehr viel stärker von den spezifischen Eigenheiten des jeweiligen Planungsproblems und von der gewählten Modellierung ab. Ein Optimierungsproblem mit hundert ganzzahligen Variablen kann aus praktischer Sicht unlösbar sein, während andere Probleme mit tausenden ganzzahliger Variablen innerhalb weniger Sekunden gelöst werden. Es gibt zwar auch in der ganzzahligen Optimierung Standardmethoden, mit denen durch große algorithmische Fortschritte innerhalb der letzten zehn Jahre mittlerweile viele praktische Planungsprobleme als IP gelöst werden können, aber gerade die Lösung großer ganzzahliger Programme in annehmbarer Zeit erfordert oft eine geschickte Modellierung und eine Kombination mehrerer Lösungsverfahren mit problemspezifischen Anpassungen.

Exakte und heuristische Verfahren

Bei der Klassifizierung der Algorithmen ist zu unterscheiden zwischen exakten und heuristischen Lösungsverfahren.

Heuristische Verfahren liefern typischerweise zulässige Lösungen in relativ kurzer Zeit, aber keine Information darüber, wie gut diese im Vergleich zu einer Optimallösung sind. Wenn eine Heuristik keine Lösung findet, ist nicht bekannt, ob dies am Algorithmus liegt oder ob das betrachtete Optimierungsproblem prinzipiell unlösbar ist. Heuristische Verfahren sind meist an das zu lösende Problem angepasst, wie beispielsweise die k-Opt-Heuristiken für das Problem des Handlungsreisenden. Bei Metaheuristiken wie Tabu-Suche ist zwar der grundsätzliche Ablauf generisch, aber die einzelnen Schritte des Algorithmus müssen abhängig vom betrachteten Problem definiert werden.

Exakte Verfahren finden beweisbar stets eine optimale Lösung oder stellen fest, dass das Problem unlösbar oder unbeschränkt ist, vorausgesetzt, man lässt den Algorithmus beliebig lange laufen. Beispiele hierfür sind Branch-and-Bound, Schnittebenenverfahren sowie deren Kombination Branch-and-Cut. In der Praxis kann man diese Verfahren durch Anpassung an das zu lösende Problem und durch Kombination mit Heuristiken oft deutlich beschleunigen. Ein eleganter Weg, schnell eine exakte Lösung zu finden, besteht darin, den Suchraum – das konvexe Polyeder im n-dimensionalen Raum, das alle möglichen Lösungen enthält – von vornherein so zu modellieren, dass er nur ganzzahlige Extremalpunkte enthält. Dies ist beispielsweise für total unimodulare Matrizen der Fall. Das Polyeder wird also nicht nachträglich mit Schnittebenen verkleinert. Gelingt das – zum Beispiel durch Lift-and-Project –, dann kann man die Optimierungsaufgabe einfach zum Beispiel durch Ausführen des Simplex-Algorithmus lösen.

Duale Schranken und Optimalitätsbeweis

Obere und untere Schranken

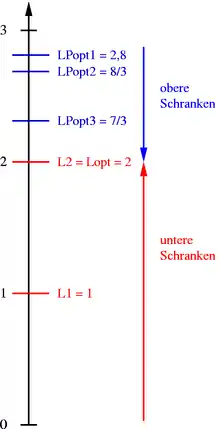
Alle praktisch relevanten exakten Verfahren beruhen auf der iterativen Lösung und Modifikation einer Relaxierung, also eines einfacheren Problems, dessen Lösungsmenge alle Lösungen des Ursprungsproblems enthält. Beispielsweise verwenden Branch-and-Bound und Schnittebenenverfahren die LP-Relaxierung, lassen also zunächst die Ganzzahligkeitsbedingungen weg. Dies lässt sich auch geometrisch interpretieren: Eigentlich ist eine optimale Ecke des IP-Polyeders $P_{I}$ (im obigen Bild rot gestrichelt) gesucht, das von allen zulässigen ganzzahligen Punkten aufgespannt wird. Da dieses Polyeder meist nicht genau bekannt ist, wird stattdessen eine optimale Ecke des Polyeders $P$ der LP-Relaxierung gesucht, das $P_{I}$ enthält (im obigen Beispiel blau umrandet). Dies geht verhältnismäßig einfach, z. B. mit dem Simplex-Verfahren.

Da in der Relaxierung mehr Lösungen zugelassen sind als im Ausgangsproblem, ist ihr Optimalwert mindestens so hoch (bei einem Maximierungsproblem) wie der – unbekannte – Optimalwert des IPs, liefert also für diesen eine obere (allgemein: duale) Schranke. Gleichzeitig definiert der Wert jeder zulässigen ganzzahligen Lösung $L$ eine untere (allgemein: primale) Schranke für den Wert einer Optimallösung, da diese ja per Definition mindestens so gut ist wie $L$ . Durch Vergleich der oberen und unteren Schranken kann ein maximaler relativer Abstand, der sogenannte Optimalitätsgap, zwischen dem Wert einer gefundenen Lösung und dem Optimalwert angegeben werden, ohne diesen genau zu kennen.

Im obigen Beispiel beträgt der optimale Wert der LP-Relaxierung 2,8. Der Optimalwert des ganzzahligen Problems kann nicht höher sein, da dort weniger Lösungen zugelassen sind als in der LP-Relaxierung. Der Punkt $(1;1)$ , den man beispielsweise durch Raten oder über eine Heuristik gefunden haben kann, ist eine zulässige Lösung des ganzzahligen Problems und hat den Zielfunktionswert 1. Eine optimale Lösung ist per Definition mindestens genauso gut wie die gefundene Lösung. Der Optimalwert des ganzzahligen Problems muss also zwischen 1 und 2,8 liegen. Der absolute Optimalitätsgap ist die Differenz zwischen der oberen und unteren Schranke, hier also $(2{,}8-1)=1{,}8.$ Der häufiger angegebene relative Optimalitätsgap ergibt sich durch Normierung dieses Wertes mit der unteren Schranke, in diesem Fall also als $1{,}8/1=1{,}8=180\,\%.$ Er besagt, dass der Optimalwert des ganzzahligen Programms um höchstens 180 % höher liegt als der Wert der Lösung $(1;1)$ . Dies erlaubt eine (in diesem Fall nicht besonders gute) Qualitätsabschätzung der Lösung. Der tatsächliche Unterschied beträgt $(2-1)/1=1=100\,\%$ , d. h. der Optimalwert ist doppelt so hoch wie der Wert der gefundenen Lösung.

Im Laufe des Algorithmus wird die Relaxierung schrittweise verschärft (beispielsweise durch Hinzufügen zusätzlicher Ungleichungen), so dass die sich daraus ergebende obere Schranke immer kleiner wird. Gleichzeitig wird versucht, bessere zulässige Lösungen zu finden, um die untere Schranke anzuheben. Dies ist in der nebenstehenden Abbildung illustriert. Sind der Wert einer gefundenen Lösung und die duale Schranke gleich (im Beispiel beim Wert 2), ist dies der Beweis, dass die gefundene Lösung optimal ist.

Im Folgenden werden einige wichtige exakte und heuristische Lösungsverfahren etwas genauer vorgestellt.

Schnittebenenverfahren

Hinzufügen einer Schnittebene (grün)

Schnittebenenverfahren (englisch cutting plane algorithm) berechnen zunächst eine Lösung der LP-Relaxierung. Diese ist meist nicht ganzzahlig, liefert aber eine duale Schranke für den Optimalwert des IPs. Diese duale Schranke wird anschließend durch schrittweises Hinzufügen sogenannter Schnittebenen verschärft. Eine Schnittebene ist eine zusätzliche Ungleichung, die von allen zulässigen Punkten des IPs erfüllt wird, aber nicht von der aktuellen LP-Lösung. Wird die Ungleichung dem LP hinzugefügt, muss daher beim erneuten Lösen eine andere Lösung herauskommen. Dies wird solange fortgeführt, bis eine ganzzahlige Lösung gefunden wird (die dann automatisch auch optimal für das ganzzahlige Programm ist) oder keine geeigneten Ungleichungen mehr gefunden werden.

Geometrisch entspricht dieses Vorgehen dem Hinzufügen einer Hyperebene, welche die optimale Ecke des LP-Polyeders $P$ von dem (unbekannten) Polyeder abschneidet, das von den ganzzahligen Lösungen aufgespannt wird. Beim erneuten Lösen wird eine optimale Ecke des beschnittenen Polyeders bestimmt. Ist diese ganzzahlig, so hat man eine zulässige und optimale Lösung des ganzzahligen linearen Programms gefunden. Andernfalls wird wieder nach einer neuen Schnittebene gesucht.

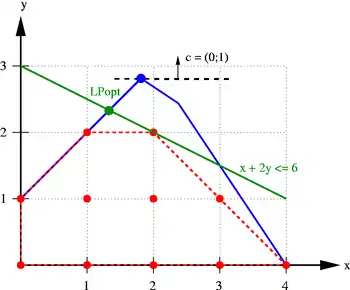
Im nebenstehenden Bild ist die Schnittebene $x+2y\leq 6$ (grün) dargestellt, die das bisherige LP-Optimum (blau) vom IP-Polyeder trennt (separiert). Alle zulässigen Punkte liegen auf einer Seite der Hyperebene, die LP-Lösung auf der anderen Seite. Erneutes Lösen des LPs mit dieser zusätzlichen Ungleichung liefert den grün markierten Punkt (4/3;7/3). Dieser Punkt ist immer noch nicht zulässig, hat aber den kleineren Zielfunktionswert 7/3, wodurch sich beispielsweise der relative Optimalitätsgap für die Lösung (1;1) von 180 % auf $(7/3-1)/1=4/3\approx 133\,\%$ verringert.

In der praktischen Anwendung sind Schnittebenenverfahren ein wichtiges Hilfsmittel, reichen aber allein meist nicht aus und können bei unvorsichtiger Anwendung zu numerischen Problemen führen. Stattdessen werden sie häufig mit Branch-and-Bound kombiniert. Wie gut das funktioniert, hängt stark von der Struktur des zu lösenden Problems ab. Die besten Schnittebenen, die man finden kann, sind Facetten des IP-Polyeders. Im obigen Beispiel sind das die Ungleichungen $y\leq 2$ und $x+y\leq 4$ , die den rot gestrichelten Linien entsprechen. Um solche Ungleichungen zu identifizieren, ist meist eine genauere mathematische Untersuchung der zugrundeliegenden Polyeder notwendig.

Branch-and-Bound bzw. Branch-and-Cut

Branching auf der Variablen x

Auch Branch-and-Bound beginnt mit dem Lösen der LP-Relaxierung. Ist die erhaltene Lösung nicht ganzzahlig, wird das Problem so in zwei oder mehr Teilprobleme zerlegt, dass jede zulässige Lösung in einem dieser Teilprobleme enthalten ist. Auf diese Art wird ein Verzweigungsbaum mit der LP-Relaxierung als Wurzelknoten aufgebaut. An jeder Verzweigung (englisch branch) wird der Wertebereich einer oder mehrerer Variablen eingeschränkt. Dies wird solange durchgeführt, bis eine beste ganzzahlige Lösung gefunden wurde.

In dieser reinen Form entspricht das Verfahren einer vollständigen Enumeration aller möglichen Lösungen. Mit Hilfe der dualen Schranken, die man durch die Lösung der Relaxierungen an jedem Knoten des Verzweigungsbaums erhält, können aber Teilbäume abgeschnitten werden (engl. bound), wenn sich erweist, dass sie keine Optimallösung enthalten können. Als alleiniger Algorithmus reicht Branch-and-Bound meist nicht aus, weil zu wenig vom Suchbaum abgeschnitten werden kann. Gute IP-Löser kombinieren dieses Verfahren daher zur Verbesserung der dualen Schranke mit Schnittebenenverfahren. Dieser Ansatz heißt dann Branch-and-Cut.

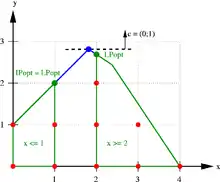
Im nebenstehenden Beispiel werden, ausgehend von der gebrochenen LP-Lösung $(1{,}8;2{,}8)$ , die beiden Teilprobleme betrachtet, die durch Hinzufügen der zusätzlichen Bedingung $x\leq 1$ bzw. $x\geq 2$ entstehen. Jede zulässige Lösung ist in genau einem der beiden Teilpolyeder (grün umrandet) enthalten. Das Lösen der LP-Relaxierung mit den zusätzlichen Bedingungen liefert im rechten Teilproblem die gebrochene Lösung $(2;8/3)$ mit dem Zielfunktionswert $8/3$ und im linken Teilproblem die ganzzahlige Lösung $(1;2)$ mit dem Wert 2. Dadurch verbessert sich die untere Schranke für den optimalen IP-Wert auf 2 (der Wert der besten bekannten zulässigen Lösung), während sich die obere Schranke auf $8/3$ verringert (der höhere LP-Wert der beiden Teilprobleme). Der Optimalitätsgap reduziert sich damit auf $(8/3-2)/2=1/3$ , d. h. der Optimalwert ist höchstens $(1+1/3)$ mal so hoch wie der Wert der Lösung $(1;2)$ . Tatsächlich ist diese Lösung bereits optimal, da sie eine ganzzahlige Lösung einer Relaxierung des ursprünglichen Problems ist.

Lagrange-Relaxierung

Die Lagrange-Relaxierung ist ein Verfahren aus der nichtlinearen Optimierung, das auch auf die ganzzahlige Optimierung angewandt werden kann. Die Grundidee besteht darin, „störende“ Ungleichungen wegzulassen, so dass das verbleibende Problem (mit Ganzzahligkeitsbedingungen) leicht lösbar ist, und stattdessen die Verletzung dieser Ungleichungen, gewichtet mit sogenannten Lagrange-Multiplikatoren, in der Zielfunktion zu bestrafen.

Eine Lösung dieses einfacheren Problems wird in den meisten Fällen die in die Zielfunktion relaxierten Bedingungen nicht erfüllen. Um dies zu ändern, werden die Lagrange-Multiplikatoren mit Hilfe eines Subgradientenverfahrens abhängig von der aktuellen (unzulässigen) Lösung so angepasst, dass ein erneutes Lösen mit den neuen Gewichten eine etwas „zulässigere“ Lösung erzeugt, welche die relaxierten Ungleichungen weniger stark verletzt. Dieser Prozess wird iterativ wiederholt, bis alle Bedingungen erfüllt sind. Man kann zeigen, dass jede Lösung einer Lagrange-Relaxierung eine duale Schranke für das ursprüngliche IP liefert, und dass dieses Verfahren bei geeigneter Anpassung der Multiplikatoren konvergiert.

Heuristiken

Für fast jedes Optimierungsproblem lassen sich leicht eine Vielzahl von Heuristiken finden, die für dieses spezielle Problem schnell zulässige Lösungen finden. Dagegen ist die Entwicklung heuristischer Verfahren, die zuverlässig gute Lösungen finden, und das möglichst auch noch für eine ganze Klasse verwandter Optimierungsprobleme und nicht nur für ein spezielles Problem, eine nicht triviale Aufgabe.

Beispiele für problemspezifische Heuristiken beim Problem des Handlungsreisenden sind die Minimum-Spanning-Tree-Heuristik zur Konstruktion einer zulässigen Tour mit Hilfe eines minimal aufspannenden Baumes und die k-Opt-Heuristiken zur Verbesserung einer bereits gefundenen Tour. Dieses Optimierungsproblem ist auch eines der wenigen Beispiele, bei denen sich leicht heuristische duale Schranken angeben lassen. Beispielsweise enthält jede Tour durch $n$ Knoten auch genau $n$ Kanten, so dass eine kürzeste Tour mindestens so lang sein muss wie die Summe der $n$ kürzesten Kantenlängen. Im Allgemeinen ist es deutlich schwieriger, gute duale Schranken anzugeben.

Neben solchen speziell für ein Problem entwickelten Verfahren gibt es sogenannte Metaheuristiken, die auf problemunabhängige Weise Strategien zur Suche zulässiger Lösungen beschreiben. Die einzelnen Schritte dieser Algorithmen müssen allerdings speziell auf das zu lösende Problem angepasst werden. Beispiele hierfür sind das Runden von LP-Lösungen, lokale Suche, Tabu-Suche, Evolutionäre Algorithmen, Simulated Annealing, Variable Nachbarschaftssuche und Ameisenalgorithmen. Einige dieser Verfahren haben Prozesse wie die natürliche Selektion oder das Verhalten von Ameisen auf der Suche nach Futter zum Vorbild; inwieweit das für die Lösungsqualität und die Lösungszeiten in der Praxis von Vorteil ist, ist umstritten.

Als alleiniges Lösungsverfahren haben all diese Algorithmen den Nachteil, dass sie erstens nicht immer eine Lösung finden, und zweitens meistens nichts über die Qualität gefundener Lösungen im Vergleich zu einer Optimallösung bekannt ist. Sie können aber beispielsweise sehr sinnvoll im Rahmen eines Branch and Cut-Ansatzes eingesetzt werden, um an verschiedenen Knoten des Suchbaumes beispielsweise aus der aktuellen LP-Lösung gute zulässige Lösungen zu generieren und so evtl. Teile des Baumes abschneiden zu können.

Literatur

Bücher

Wolfgang Domschke, Andreas Drexl, Robert Klein, Armin Scholl: Einführung in Operations Research. 9. Auflage. Springer, Berlin 2015, ISBN 978-3-662-48215-5 (speziell Kap. 6).
Josef Kallrath: Gemischt-Ganzzahlige Optimierung. Modellierung in der Praxis. Vieweg, Wiesbaden 2002, ISBN 3-528-03141-7.
Richard K. Martin: Large Scale Linear and Integer Optimization. A Unified Approach. Kluwer Academic Publishers, Boston, Mass. 2004, ISBN 0-7923-8202-1.
George Nemhauser, Laurence Wolsey: Integer and Combinatorial Optimization. Wiley Interscience, New York 1999, ISBN 0-471-35943-2.
Leena Suhl, Taieb Mellouli: Optimierungssysteme. Modelle, Verfahren, Software, Anwendungen. Springer, Berlin 2006, ISBN 3-540-26119-2.

Aufsätze

Robert J. Dakin: A tree-search algorithm for mixed integer programming problems. In: The Computer Journal, Bd. 8 (1965), S. 250–255.
Ralph Gomory: Early Integer Programming. In: Operations Research, Bd. 50 (2002), Nummer 1, S. 78–81.
Ailsa H. Land, Alison G. Doig: An automatic method of solving discrete programming problems. In: Econometrica, Bd. 28 (1960), S. 497–520.

Weblinks

Linear Programming FAQ, Abschnitt über Integer Programming (englisch)
Vergleich nichtkommerzieller Codes zum Lösen von MIPs (englisch) von Hans Mittelmann, Arizona State University, mit Links zu den Codes
Optimierung in der Praxis (englisch)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.