Schnittebenenverfahren

Ein Schnittebenenverfahren (engl. cutting plane algorithm) ist in der angewandten Mathematik ein Algorithmus zur Lösung ganzzahliger linearer Optimierungsprobleme. Die Grundidee besteht darin, statt eines ganzzahligen linearen Programms seine LP-Relaxation (also ohne Ganzzahligkeitsbedingungen) zu betrachten und diese durch Hinzufügung weiterer Ungleichungen schrittweise zu verschärfen, bis (im Idealfall) eine ganzzahlige Lösung gefunden wird.

Das in den 1950er Jahren u. a. von Delbert Ray Fulkerson, George Dantzig und später von Egon Balas und Ralph Gomory entwickelte Verfahren ist mit seinen Weiterentwicklungen heute eine der Standardmethoden in der ganzzahligen Optimierung und weiterhin Gegenstand aktueller Forschung. Als alleiniges Lösungsverfahren ist es meist nicht ausreichend, liefert aber gute duale Schranken für die zu lösenden Optimierungsprobleme. Daher wird es oft mit Branch-and-Bound zum sogenannten Branch-and-Cut-Verfahren kombiniert.

Problemdefinition

Ein Schnittebenenverfahren dient zur Lösung ganzzahliger Programme (engl. integer program, IP) in der Normalform

\max\{c^{T}x\;|\;Ax\leq b,x\geq 0,x\in \mathbb {Z} ^{n}\}.

Dabei ist $A$ eine reelle Matrix und $b$ und $c$ sind Vektoren passender Dimension. Die Bedingung $Ax\leq b$ ist komponentenweise zu verstehen, also als

a_{i}\cdot x=\sum _{j=1}^{n}a_{ij}x_{j}\leq b_{i}

für alle Zeilen $i$ der Matrix $A$ . Genauso bedeutet die Bedingung $x\geq 0$ , dass alle Einträge des Vektors $x$ nichtnegativ sein müssen.

Polytop der zulässigen ganzzahligen Punkte (rot) mit LP-Relaxierung (blau)

Dies kann wie folgt geometrisch interpretiert werden: die Menge

P:=\{x\;|\;Ax\leq b,x\geq 0\},

die durch Weglassen der Ganzzahligkeitsbedingungen entsteht, bildet ein konvexes Polyeder im $n$ -dimensionalen Raum, dessen beschränkende Hyperebenen den Zeilen des Ungleichungssystems entsprechen. $P$ enthält u. a. alle zulässigen Punkte des Ausgangssystems, also alle ganzzahligen Punkte, die die Bedingungen $Ax\leq b$ erfüllen, aber im Unterschied zur linearen Optimierung sind nicht alle Punkte in $P$ zulässig. Das lineare Programm

\max \,\{c^{T}x\;|\;x\in P\}

wird als LP-Relaxierung des ganzzahligen Problems bezeichnet.

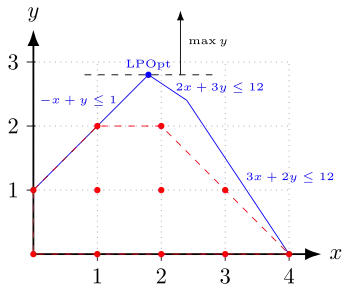
Im nebenstehenden Bild ist das ganzzahlige lineare Programm (IP)

{\begin{matrix}\max &&y\\&-x&+y&\leq 1\\&3x&+2y&\leq 12\\&2x&+3y&\leq 12\\&x,y\in \mathbb {Z} _{+}\end{matrix}}

dargestellt. Die zulässigen ganzzahligen Punkte sind rot eingezeichnet, und die rot gestrichelten Linien kennzeichnen ihre konvexe Hülle, also das kleinste Polyeder, das alle diese Punkte enthält. Über diesem Polyeder soll eigentlich optimiert werden, aber es ist meist nicht genau bekannt. Die blauen Linien zusammen mit den Koordinatenachsen begrenzen das Polyeder $P$ der LP-Relaxierung, das durch das Ungleichungssystem ohne Ganzzahligkeitsbedingungen gegeben ist. Ziel der Optimierung ist es, die schwarz gestrichelte Linie so weit parallel nach oben (in Richtung des Vektors $c=(0;1)$ ) zu verschieben, dass sie das jeweilige Polyeder gerade noch berührt. Die Optimallösungen des ganzzahligen Problems sind also die Punkte $(1;2)$ und $(2;2)$ mit dem Zielfunktionswert $c^{T}x=(0;1)^{T}(1;2)=2$ . Die – in diesem Fall eindeutige – optimale Lösung der LP-Relaxierung mit dem Zielfunktionswert 2,8 ist der blau markierte Punkt $LP_{opt}=(1,8;2,8)$ , der nicht ganzzahlig und damit auch nicht zulässig für das IP ist.

Grundidee des Algorithmus am Beispiel

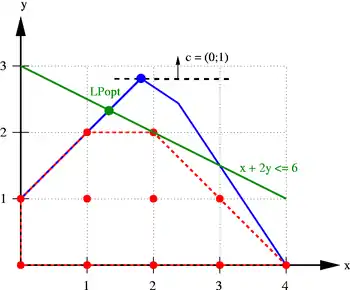
Hinzufügen einer Schnittebene (grün)

Schnittebenenverfahren berechnen zunächst eine Lösung der LP-Relaxierung. Diese ist meist nicht ganzzahlig (wie der Punkt $LP_{opt}=(1{,}8;2{,}8)$ ), liefert aber eine obere (allgemein: duale) Schranke für den Optimalwert des IPs, da jede Lösung des ganzzahligen Programms auch eine Lösung der LP-Relaxierung ist und deshalb der Optimalwert des ganzzahligen Programms (im Beispiel 2) höchstens so hoch sein kann wie der Optimalwert der LP-Relaxierung (im Beispiel 2,8). Dies kann zur Abschätzung der Qualität einer Lösung des IPs genutzt werden.

Diese duale Schranke wird anschließend durch schrittweises Hinzufügen sogenannter Schnittebenen verschärft. Eine Schnittebene ist eine zusätzliche Ungleichung, die von allen zulässigen Punkten des IPs erfüllt wird, aber nicht von der aktuellen LP-Lösung. Wird die Ungleichung dem LP hinzugefügt, muss daher beim erneuten Lösen eine andere Lösung herauskommen. Dies wird solange fortgeführt, bis eine ganzzahlige Lösung gefunden wird (die dann automatisch auch optimal für das ganzzahlige Programm ist) oder keine geeigneten Ungleichungen mehr gefunden werden.

Im nebenstehenden Bild ist die Schnittebene $x+2y\leq 6$ (grün) dargestellt, die das bisherige LP-Optimum (blau) vom IP-Polyeder trennt (separiert). Alle zulässigen Punkte liegen auf einer Seite der Hyperebene, die LP-Lösung auf der anderen Seite. Erneutes Lösen des LPs mit dieser zusätzlichen Ungleichung liefert den grün markierten Punkt (4/3;7/3). Dieser Punkt ist immer noch nicht zulässig, hat aber den kleineren Zielfunktionswert $7/3\approx 2{,}333$ , was die obere Schranke auf diesen Wert verbessert.

Die besten Schnittebenen, die man finden kann, sind Facetten des IP-Polyeders, also $(n-1)$ -dimensionale Seitenflächen bei $n$ Variablen. Im obigen Beispiel sind das die Ungleichungen $y\leq 2$ und $x+y\leq 4$ , die den rot gestrichelten Linien entsprechen.

Einsatz in der Praxis

Für eine ganze Reihe von Planungsproblemen, vor allem solchen mit praktischen Anwendungshintergrund (z. B. Routingprobleme oder Zuordnungsprobleme), sind mehrere Klassen von Ungleichungen bekannt, die von allen ganzzahligen Punkten des Polyeders erfüllt werden (also für dieses Polyeder gültig sind). Dies können problemunabhängige IP-Schnittebenen wie Gomory-Cuts sein, die auch ohne Kenntnis des praktischen Hintergrunds von Standardlösern gefunden werden können, oder problemspezifische Schnittebenen, die die spezielle Struktur der Matrix $A$ ausnutzen. Beispiele für letztere sind die Kurzzyklusungleichungen beim Problem des Handlungsreisenden. Da es im Verhältnis zur Anzahl der Knoten des Graphen exponentiell viele Kurzzyklusungleichungen gibt, kann man sie zunächst weglassen und stattdessen nach und nach separieren.

Solche Klassen gültiger Ungleichungen für bestimmte Arten oder Teilstrukturen von ganzzahligen Programmen zu finden und Aussagen über die Qualität dieser Schnittebenen zu treffen, ist ein nicht triviales Problem. Insbesondere die Information, unter welchen Bedingungen eine Schnittebene eine Facette des zugrundeliegenden Polyeders definiert, erfordert in der Regel eine genauere mathematische Untersuchung. Dies ist ein wichtiger Gegenstand aktueller Forschung in der ganzzahligen linearen Optimierung.

Sind einige Klassen gültiger Ungleichungen bekannt, wird meist folgender Algorithmus angewendet:

Löse die LP-Relaxierung; sei $x^{*}$ die Optimallösung des LPs.
Wenn $x^{*}$ ganzzahlig ist, ist es auch optimal. STOP.
Teste für alle bekannten Klassen von Ungleichungen, ob sie eine oder mehrere von $x^{*}$ verletzte Schnittebenen enthält.
Falls ja, füge sie zum LP hinzu und gehe zu 1. Sonst STOP.

Wird am Ende keine verletzte Schnittebene mehr gefunden, ohne dass die LP-Lösung ganzzahlig ist, kann man versuchen, heuristisch eine ganzzahlige Lösung zu bestimmen oder Branch-and-Bound zu starten (diese Kombination heißt dann Branch-and-Cut). Dies funktioniert in der Praxis je nach Problem und verwendetem Modell mal mehr und mal weniger gut.

Wie man in Schritt (3) die Ungleichungen auf Verletzung testet, hängt von den Ungleichungen ab. In einigen Fällen kann man die Schnittebenen exakt separieren, d. h. wenn man keine verletzte Ungleichung dieser Klasse findet, gibt es auch keine. Dies ist zum Beispiel dann der Fall, wenn eine Klasse so wenige Ungleichungen enthält, dass man sie einfach alle durchtesten kann. Aber auch die exponentiell vielen Kurzzyklusungleichungen im Falle des TSP können durch Berechnung eines minimalen Schnittes im zugrundeliegenden Graphen in Polynomialzeit auf Verletzung getestet werden. In anderen Fällen, wo die Separierung in annehmbarer Zeit nur heuristisch möglich ist (beispielsweise bei allgemeinen Mixed-Integer Rounding Cuts), ist am Ende nicht klar, ob es keine verletzten Ungleichungen mehr gibt oder ob man sie nur nicht gefunden hat.

Geschichte

Die ersten Schnittebenen wurden Mitte der 1950er Jahre von D.R. Fulkerson, G. Dantzig und S. Johnson für das Problem des Handlungsreisenden entwickelt. Ohne Kenntnis dieser Arbeiten und motiviert durch ehemalige Kollegen der US Navy, die an ganzzahligen Lösungen interessiert waren, entwickelte R. Gomory im Jahre 1958 während seines Aufenthaltes in Princeton das erste allgemein einsetzbare Schnittebenenverfahren. Er zeigte, dass theoretisch allein mit diesem Verfahren beliebige ganzzahlige Programme gelöst werden können. In der Praxis hat dieser Ansatz allerdings zwei Probleme: einerseits führen viele Schnittebenen irgendwann zu sehr großen linearen Programmen und entsprechend langen Lösungszeiten in jeder Iteration, und andererseits enthalten die von Gomory vorgeschlagenen Schnittungleichungen (Gomory fractional cuts) oft sehr viele Nicht-Null-Koeffizienten, was zu numerischen Instabilitäten bei der Lösung der linearen Programme führt. Trotzdem stellte dieses Verfahren einen entscheidenden algorithmischen Fortschritt dar.

In den 1980er Jahren arbeiteten M. Padberg und andere an Schnittebenen für oft auftauchende Teilstrukturen wie Rucksackprobleme, die oft auch in allgemeinerem Kontext eingesetzt werden können. In den letzten zehn Jahren wurden viele Schnittebenen für spezielle Anwendungsprobleme entdeckt, etwa für Routingprobleme, die im Zusammenhang mit der Planung öffentlicher Nahverkehrsnetze oder beim Design von Telekommunikationsnetzen auftreten.

Literatur

George Nemhauser und Laurence Wolsey: Integer and Combinatorial Optimization. Wiley Interscience, 1988, ISBN 0-471-35943-2.
Ralph Gomory: Early Integer Programming. In: Operations Research, Volume 50, Nummer 1, S. 78–81, 2002.

Weblinks

Beschreibung von Schnittebenen für das Problem des Handlungsreisenden (engl.)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.