Gaußsches Eliminationsverfahren

Das gaußsche Eliminationsverfahren oder einfach Gauß-Verfahren (nach Carl Friedrich Gauß) ist ein Algorithmus aus den mathematischen Teilgebieten der linearen Algebra und der Numerik. Es ist ein wichtiges Verfahren zum Lösen von linearen Gleichungssystemen und beruht darauf, dass elementare Umformungen zwar das Gleichungssystem ändern, aber die Lösung erhalten. Dies erlaubt es, jedes eindeutig lösbare Gleichungssystem auf Stufenform zu bringen, an der die Lösung durch sukzessive Elimination der Unbekannten leicht ermittelt oder die Lösungsmenge abgelesen werden kann.

Die Anzahl der benötigten Operationen ist bei einer $n\times n$ -Matrix von der Größenordnung $n^{3}$ . In seiner Grundform ist der Algorithmus aus numerischer Sicht anfällig für Rundungsfehler, aber mit kleinen Modifikationen (Pivotisierung) stellt er für allgemeine lineare Gleichungssysteme das Standardlösungsverfahren dar und ist Teil aller wesentlichen Programmbibliotheken für numerische lineare Algebra wie NAG, IMSL und LAPACK.

Erklärung

Ein lineares Gleichungssystem $Ax=b$ mit drei Gleichungen und drei Unbekannten $x=(x_{1},~x_{2},~x_{3})^{T}$ und rechter Seite $b=(b_{1},~b_{2},~b_{3})^{T}$ hat die Form:

{\begin{array}{rcrcrcl}a_{11}x_{1}&+&a_{12}x_{2}&+&a_{13}x_{3}&=&b_{1},\\a_{21}x_{1}&+&a_{22}x_{2}&+&a_{23}x_{3}&=&b_{2},\\a_{31}x_{1}&+&a_{32}x_{2}&+&a_{33}x_{3}&=&b_{3}.\end{array}}

Der Algorithmus zur Berechnung der Variablen $x_{1}$ , $x_{2}$ und $x_{3}$ lässt sich in zwei Etappen einteilen:

Vorwärtselimination,
Rückwärtseinsetzen (Rücksubstitution).

Im ersten Schritt wird das Gleichungssystem auf Stufenform gebracht. Stufenform heißt, dass pro Zeile mindestens eine Variable weniger auftritt, also mindestens eine Variable eliminiert wird. Im obigen Gleichungssystem würde man $a_{21}$ , $a_{31}$ und $a_{32}$ eliminieren, in der dritten Zeile ist dann nur noch die Variable $x_{3}$ :

{\begin{array}{rcrcrcl}{\tilde {a}}_{11}x_{1}&+&{\tilde {a}}_{12}x_{2}&+&{\tilde {a}}_{13}x_{3}&=&{\tilde {b}}_{1}\\&&{\tilde {a}}_{22}x_{2}&+&{\tilde {a}}_{23}x_{3}&=&{\tilde {b}}_{2}\\&&&&{\tilde {a}}_{33}x_{3}&=&{\tilde {b}}_{3}.\end{array}}

Zum Erreichen der Stufenform werden elementare Zeilenumformungen benutzt, mit Hilfe derer das Gleichungssystem in ein neues transformiert wird, welches aber dieselbe Lösungsmenge besitzt. Ausreichend sind zwei Arten von elementaren Zeilenumformungen:

Eine Zeile oder das Vielfache einer Zeile zu einer anderen Zeile addieren.
Zwei Zeilen vertauschen.

Das Verfahren besteht dann darin, angefangen in der ersten Spalte mit Umformungen der ersten Art durch geschicktes Dazuaddieren der ersten Zeile alle Einträge bis auf den ersten zu Null zu machen. Dies wird dann in der so modifizierten zweiten Spalte fortgesetzt, wobei diesmal Vielfache der zweiten Zeile zu den folgenden Zeilen addiert werden und so weiter. Dieser Schritt funktioniert nur, wenn das Diagonalelement der aktuellen Spalte nicht Null ist. In so einem Fall ist die zweite Art der Zeilenumformung nötig, da durch eine Zeilenvertauschung ein Nichtnulleintrag auf der Diagonale erzeugt werden kann. Mit Hilfe dieser beiden Arten von Umformungen ist es möglich, jedes lineare Gleichungssystem auf Stufenform zu bringen.

Eine weitere Art der elementaren Umformung ist das Vertauschen von Spalten. Diese wird zur Durchführung des Algorithmus nicht benötigt, aber manchmal in Computerprogrammen aus Stabilitätsgründen eingesetzt. Dabei wird die Position der Variablen im Gleichungssystem geändert. Beim Rechnen per Kopf ist manchmal noch die Multiplikation einer Zeile mit einer Zahl nützlich, etwa um komplizierte Brüche zu vermeiden. Dies verursacht zusätzlichen Rechenaufwand und ist deswegen in Computerprogrammen keine Option und ändert ferner die Determinante der Koeffizientenmatrix, was theoretische Nachteile mit sich bringt.

Im zweiten Schritt des Verfahrens, dem Rückwärtseinsetzen, werden ausgehend von der letzten Zeile, in der nur noch eine Variable auftaucht, die Variablen ausgerechnet und in die darüberliegende Zeile eingesetzt.

Eine Alternative hierzu ist der Gauß-Jordan-Algorithmus, bei dem nicht nur die unteren Teile eliminiert werden, sondern auch die oberen, so dass eine Diagonalform entsteht, bei der dann der oben genannte zweite Schritt entfällt.

Eine weitere Möglichkeit ist die Benutzung einer erweiterten Matrix mit drei Untermatrizen, in denen mit fortschreitender Rechnung die Permutationsmatrix für die Zeilenvertauschungen zwecks #Pivotisierung und die Dreiecksmatrizen für die #LR-Zerlegung entstehen, siehe Äquivalenztransformation#Gauß’sches Eliminationsverfahren.

Beispiel

$x_{1}+2x_{2}+3x_{3}=2$ , hier: $a_{11}=1$ , $a_{12}=2$ , $a_{13}=3$ und $b_{1}=2$
$x_{1}+x_{2}+x_{3}=2$
$3x_{1}+3x_{2}+x_{3}=0$

Zur besseren Übersichtlichkeit werden die Koeffizienten $a_{ij}$ des linearen Gleichungssystems in die mit $b$ erweiterte Koeffizientenmatrix geschrieben:

\left({\begin{array}{c c c | c}1&2&3&2\\1&1&1&2\\3&3&1&0\end{array}}\right)

Jetzt wird so umgeformt, dass $a_{21}$ und $a_{31}$ Null werden, indem man geeignete Vielfache der ersten Gleichung zur zweiten und dritten Gleichung addiert. Den entsprechenden Multiplikator erhält man, indem man das zu eliminierende Element (als erstes $a_{21}=1$ ) durch das Pivotelement $a_{11}$ teilt (hier: ${\tfrac {1}{1}}=1$ und ${\tfrac {3}{1}}=3$ ). Da die beiden Elemente $a_{21}$ und $a_{31}$ Null werden sollen, werden die beiden Multiplikatoren jeweils mit $(-1)$ multipliziert.

Zur zweiten Zeile wird also das $(-1)$ -fache und zur dritten Zeile das $(-3)$ -fache der ersten Zeile addiert. Damit $a_{32}$ Null wird, wird ein Vielfaches der zweiten Zeile zur dritten Zeile addiert, in diesem Fall das $(-3)$ -fache:

Falls die Zahl, durch die zur Berechnung des Multiplikators dividiert wird (hier für die ersten beiden Zeilen die Zahl $1$ , beim dritten Mal die Zahl $-1$ ), Null ist, wird diese Zeile mit einer weiter unten liegenden vertauscht. Die letzte Zeile bedeutet

-2x_{3}=-6

.

Diese Gleichung ist einfach lösbar und liefert $x_{3}=3$ . Damit ergibt sich für die zweite Zeile

-1x_{2}-2x_{3}=0

, mit

x_{3}=3

also

x_{2}=-6

und weiter $x_{1}=5$ . Damit sind alle Variablen berechnet:

x_{1}=5

,

x_{2}=-6

und

x_{3}=3

.

Kontrolle durch Zeilensumme

Die Umformungen können durch das Berechnen der Zeilensumme kontrolliert werden.

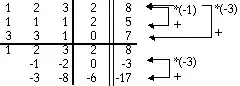
Hier wurde in der letzten Spalte die Summe aller Elemente der jeweiligen Zeile angeschrieben. Für die erste Zeile ist die Zeilensumme $1+2+3+2=8$ . Da an der ersten Zeile keine Umformungen durchgeführt werden, ändert sich ihre Zeilensumme nicht. Bei der ersten Umformung dieses Gleichungssystems wird zur zweiten Zeile das $(-1)$ -fache der ersten addiert. Macht man das auch für die Zeilensumme, so gilt $5+(-1)\cdot 8=-3$ . Dieses Ergebnis ist die Zeilensumme der umgeformten zweiten Zeile $-1-2+0=-3$ . Zur Überprüfung der Rechnungen kann man also die Umformungen an der Zeilensumme durchführen. Sind alle Rechnungen korrekt, muss sich die Zeilensumme der umgeformten Zeile ergeben.

Pivotisierung

Das gaußsche Eliminationsverfahren ist im Allgemeinen nicht ohne Zeilenvertauschungen durchführbar. Ersetzt man im obigen Beispiel $a_{11}=1$ durch $a_{11}=0$ , so kann der Algorithmus ohne Zeilenvertauschung gar nicht starten. Zur Abhilfe wählt man ein Element der ersten Spalte der Koeffizientenmatrix, das sogenannte Pivotelement, welches ungleich 0 ist.

Wahl des Pivot
$x_{1}$	$x_{2}$	$x_{3}$	$b$
0	2	3	4
1	1	1	2
3	3	1	0

Danach vertauscht man die erste Zeile mit der Pivotzeile:

Zeilenvertauschung
$x_{1}$	$x_{2}$	$x_{3}$	$b$
1	1	1	2
0	2	3	4
3	3	1	0

Für die Rechnung per Hand ist es hilfreich, eine 1 oder minus 1 als Pivotelement zu wählen, damit im weiteren Verlauf des Verfahrens keine Brüche entstehen. Für die Berechnung mit Hilfe eines Computers ist es sinnvoll, das betragsgrößte Element zu wählen, um einen möglichst stabilen Algorithmus zu erhalten. Wählt man das Pivotelement in der aktuellen Spalte, spricht man von Spaltenpivotisierung. Alternativ kann man das Pivot auch in der aktuellen Zeile wählen.

Wahl des Pivot
$x_{1}$	$x_{2}$	$x_{3}$	$b$
0	2	3	4
1	1	1	2
3	3	1	0

In diesem Fall werden entsprechend die Spalten getauscht.

Spaltenvertauschung
$x_{2}$	$x_{1}$	$x_{3}$	$b$
2	0	3	4
1	1	1	2
3	3	1	0

Beim Rückwärtseinsetzen ist dabei zu beachten, dass die Variablen ihre Position im Gleichungssystem geändert haben. Wählt man als Pivot das betragsgrößte Element der gesamten Restmatrix, so spricht man von vollständiger Pivotisierung beziehungsweise Totalpivotisierung. Dafür sind im Allgemeinen sowohl Zeilen- als auch Spaltenvertauschungen notwendig.

Pivotisierung ist ohne nennenswerten Zusatzaufwand durchführbar, wenn nicht die Einträge der Matrix und der rechten Seite vertauscht, sondern die Vertauschungen in einem Indexvektor gespeichert werden.

LR-Zerlegung

Einführendes Beispiel

Will man das Lösen eines quadratischen eindeutig lösbaren Gleichungssystems $Ax=b$ als Computerprogramm umsetzen, bietet es sich an, den Gaußalgorithmus als LR-Zerlegung (auch LU-Zerlegung oder Dreieckszerlegung genannt) zu interpretieren. Dies ist eine Zerlegung der regulären Matrix $A$ in das Produkt einer linken unteren, normierten Dreiecksmatrix $L$ (links, bzw. Englisch „left“, oder auch „lower“) und einer rechten oberen Dreiecksmatrix $R$ (rechts, bzw. Englisch „right“, oder auch „upper“, und dann mit $U$ bezeichnet). Das folgende Beispiel zeigt dies:

A={\begin{pmatrix}1&2&3\\1&1&1\\3&3&1\\\end{pmatrix}}={\begin{pmatrix}1&0&0\\1&1&0\\3&3&1\\\end{pmatrix}}\cdot {\begin{pmatrix}1&2&3\\0&-1&-2\\0&0&-2\\\end{pmatrix}}=L\cdot R

Dabei dient die Matrix $L$ dem Speichern der benötigten Umformungsschritte, die Multiplikationen mit Frobeniusmatrizen entsprechen, und $R$ hat die oben erwähnte Stufenform. Das zeigt die Existenz der Zerlegung. Um Eindeutigkeit zu erreichen, werden die Diagonalelemente der Matrix $L$ als 1 festgelegt. Die Umformungsschritte zu speichern hat den Vorteil, dass für verschiedene „rechte Seiten“ $b$ das Gleichungssystem effizient durch Vorwärts- und Rückwärtseinsetzen gelöst werden kann.

Die im Allgemeinen benötigten Zeilenvertauschungen können durch eine Permutationsmatrix $P$ beschrieben werden:

P\cdot A=L\cdot R.

Existenzsatz

Für jede reguläre Matrix $A\in \mathbb {R} ^{n\times n}$ existiert eine Permutationsmatrix $P\in \mathbb {R} ^{n\times n}$ , eine untere, normierte Dreiecksmatrix $L\in \mathbb {R} ^{n\times n}$ und eine obere Dreiecksmatrix $R\in \mathbb {R} ^{n\times n}$ , sodass gilt:

P\cdot A=L\cdot R

.

Eine Permutationsmatrix $P$ ist eine Matrix, die aus der Einheitsmatrix durch eine beliebige Anzahl an Zeilenvertauschungen entsteht und somit weiterhin nur aus Nullen und Einsen besteht.

Algorithmus

Der Algorithmus zur Berechnung der Matrizen $P,L,R$ für ein vorgegebenes $A\in \mathbb {R} ^{n\times n}$ lautet wie folgt.

Es werden $n$ Matrixumformungen vollzogen ( $k=0,\ldots ,n-1$ ). Dabei führt man die Umformungsmatrizen $A^{(k)}$ ein:

A^{(k)}=\left(a_{ij}^{(k)}\right)={\begin{cases}A&,\quad k=0\\(I-L^{(k)})P^{(k-1)}A^{(k-1)}&,\quad k=1,\ldots ,n-1.\end{cases}}

Dabei wurden neue Hilfsmatrizen $L^{(k)},P^{(k)}$ eingeführt:

{\begin{aligned}\left(L^{(k)}\right)_{ij}&={\begin{cases}{\frac {a_{ik}^{(k-1)}}{a_{kk}^{(k-1)}}}&,\quad j=k\;\wedge \;i>k\\0&,\quad {\text{sonst}}\end{cases}}\\P^{(k)}&=(e_{1},\ldots ,e_{k-1},e_{\hat {k}},e_{k+1},\ldots ,e_{{\hat {k}}-1},e_{k},e_{{\hat {k}}+1},\ldots ,e_{n})\\{\hat {k}}&\in \{k,\ldots ,n\}\quad {\text{sodass gilt}}\quad \left|a_{{\hat {k}}k}^{(k)}\right|=\max {\left\lbrace \left|a_{ik}^{(k)}\right|\colon i=k,\ldots ,n\right\rbrace }.\end{aligned}}

Beachte:

$e_{i}\in \mathbb {R} ^{n}$ stellt den $i$ -ten Basisvektor dar
in $P^{(k)}$ wurde nur eine Zeile der Einheitsmatrix mit einer anderen vertauscht
${\hat {k}}$ muss so gewählt werden, dass $a_{{\hat {k}}k}^{(k)}$ den betragsmäßig größten Wert für alle Elemente aus der Teilspalte $k$ hat

Man benötigt noch weitere Hilfsmatrizen $Q^{(k)}$ :

Q^{(k)}={\begin{cases}I&,\quad k=n\\P^{(n-1)}\cdot \ldots \cdot P^{(k)}&,\quad k<n.\end{cases}}

Nun können die gewünschten Matrizen angegeben werden:

{\begin{aligned}R&=A^{(n)}\\P&=Q^{(1)}\\L&=\left(I+\sum _{k=1}^{n-1}Q^{(k+1)}L^{(k)}\right).\end{aligned}}

Ohne Pivotisierung, $L,R$ out-of-place

Der folgende Algorithmus führt eine LR-Zerlegung der Matrix A ohne Pivotisierung aus, indem er simultan L und R außerhalb (out-of-place) von A erzeugt:

   Eingabe: Matrix A

   // Initialisierung
   R := A
   L := E_n

   // n-1 Iterationsschritte
   for i := 1 to n-1
     // Zeilen der Restmatrix werden durchlaufen
     for k := i+1 to n
       // Berechnung von L
       L(k,i) := R(k,i) / R(i,i) // Achtung: vorher Prüfung auf Nullwerte notwendig
       // Spalten der Restmatrix werden durchlaufen
       for j := i to n
         // Berechnung von R
         R(k,j) := R(k,j) - L(k,i) * R(i,j)

   Ausgabe: Matrix L, Matrix R

Ohne Pivotisierung, $L,R$ in-place

Alternativ ist (aus möglichem Interesse an Speichereffizienz) eine simultane Entwicklung von L und R direkt in A möglich (in-place), welcher durch folgenden Algorithmus beschrieben wird:

   Eingabe: Matrix A

   // n-1 Iterationsschritte
   for i := 1 to n-1
     // Zeilen der Restmatrix werden durchlaufen
     for k := i+1 to n
       // Berechnung von L
       A(k,i) := A(k,i) / A(i,i) // Achtung: vorher Prüfung auf Nullwerte notwendig
       // Spalten der Restmatrix werden durchlaufen
       for j := i+1 to n
         // Berechnung von R
         A(k,j) := A(k,j) - A(k,i) * A(i,j)

   Ausgabe: Matrix A (in modifizierter Form)

Mit Pivotisierung

Der folgende Algorithmus führt eine LR-Zerlegung der Matrix $A$ mit Pivotisierung aus. Er unterscheidet sich von den Algorithmen ohne Pivotisierung nur durch mögliche Zeilenvertauschung:

   Eingabe: Matrix  $A$

   // n-1 Iterationsschritte
   for k := 1 to n-1
     // Pivotisierung
     // finde betragsmäßig größtes Element in k-ter Spalte
      ${\hat {k}}$  = k
      ${\hat {a}}=|a_{{\hat {k}}k}^{(k-1)}|$ 
     for i := k+1 to n
       if <  $\left(|a_{ik}^{(k-1)}|>{\hat {a}}\right)$  >
          ${\hat {k}}$  = i
          ${\hat {a}}=|a_{ik}^{(k-1)}|$ 
     // vertausche Zeilen
     <Erstelle  $P^{(k)}$ >
     <Vertausche Zeilen k, ${\hat {k}}$ >
     // Rest analog zu obigen Algorithmen
     <Rest  $\ldots$ >
    $P=P^{(n)}\cdots P^{(1)}$

   Ausgabe: Matrix L, Matrix R, Matrix P

Lösen eines LGS

Das ursprüngliche LGS $Ax=b$ wird mittels der LR-Zerlegung nun wie folgt vereinfacht:

{\begin{aligned}Ax=b\quad &{\text{und}}\quad PA=LR\\\Rightarrow PAx&=Pb\\\Leftrightarrow LRx&=Pb.\end{aligned}}

Nun definiert man die folgenden Hilfsvariablen

y:=Rx\quad {\text{und}}\quad {\hat {b}}:=Pb.

Folglich hat sich das LGS $Ax=b$ in eine vereinfachte Struktur gewandelt:

Ly={\hat {b}}\quad {\text{und}}\quad Rx=y.

Diese können leicht durch Vorwärts- bzw. Rückwärtseinsetzen gelöst werden.

Vorwärtseinsetzen

Beim Vorwärtseinsetzen berechnet man eine Lösung $y$ des linearen Gleichungssystems $Ly=b$ , beziehungsweise bei Rechnung mit Pivotisierung von $Ly=Pb={\hat {b}}$ . Diese steht über die Gleichung $y=Rx$ mit der Lösung $x$ des ursprünglichen Gleichungssystems in Beziehung.

Ausgeschrieben hat das Gleichungssystem $Ly=b$ folgende Gestalt:

{\begin{pmatrix}l_{11}&0&0&\ldots &0\\l_{21}&l_{22}&0&&\vdots \\l_{31}&l_{32}&l_{33}&\ddots &\vdots \\\vdots &\vdots &\vdots &\ddots &0\\l_{n1}&l_{n2}&l_{n3}&\ldots &l_{n,n}\end{pmatrix}}\cdot {\begin{pmatrix}y_{1}\\y_{2}\\y_{3}\\\vdots \\y_{n}\end{pmatrix}}={\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\\\vdots \\b_{n}\end{pmatrix}}

Für die Komponenten $y_{i}$ gilt dann die folgende Formel:

y_{i}={\frac {1}{l_{ii}}}\left(b_{i}-\sum _{k=1}^{i-1}l_{ik}\cdot y_{k}\right).

Beginnend mit $y_{1}={\frac {b_{1}}{l_{11}}}$ können nacheinander $y_{1},y_{2},\ldots ,y_{n}$ ausgerechnet werden, indem jeweils die schon bekannten $y_{i}$ eingesetzt werden.

Rückwärtseinsetzen

Beim Rückwärtseinsetzen berechnet man die Lösung $x$ des ursprünglichen Gleichungssystems, indem man $Rx=y$ ähnlich wie beim Vorwärtseinsetzen löst. Der Unterschied besteht darin, dass man bei $x_{n}={\frac {y_{n}}{r_{nn}}}$ beginnt und dann nacheinander die Werte von $x_{n-1},x_{n-2},\ldots ,x_{1}$ berechnet. Die entsprechende Formel lautet

x_{i}={\frac {1}{r_{ii}}}\left(y_{i}-\sum _{k=i+1}^{n}r_{ik}\cdot x_{k}\right).

Unvollständige Zerlegungen

Die LR-Zerlegung hat den Nachteil, dass sie auch bei dünnbesetzten Matrizen häufig vollbesetzt ist. Werden dann statt aller Einträge nur jene in einem vorgegebenen Besetzungsmuster berechnet, spricht man von einer unvollständigen LU-Zerlegung. Diese liefert eine günstige Approximation an die Matrix $A$ und kann somit als Vorkonditionierer bei der iterativen Lösung linearer Gleichungssysteme eingesetzt werden. Im Fall symmetrisch positiv definiter Matrizen spricht man von einer unvollständigen Cholesky-Zerlegung.

Eigenschaften des Verfahrens

Rechenaufwand und Speicherplatzbedarf

Die Anzahl arithmetischer Operationen für die LR-Zerlegung ist bei einer $n\times n$ -Matrix ca. ${\tfrac {2}{3}}n^{3}$ . Der Aufwand für das Vorwärts- und Rückwärtseinsetzen ist quadratisch ( ${\mathcal {O}}(n^{2})$ ) und daher insgesamt vernachlässigbar. Das gaußsche Eliminationsverfahren ist ein schnelles direktes Verfahren zur Lösung linearer Gleichungssysteme, für eine QR-Zerlegung benötigt man mindestens doppelt so viele Rechenoperationen. Dennoch sollte der Algorithmus nur für Gleichungssysteme kleiner bis mittlerer Dimension verwendet werden (bis etwa $n=10000$ ). Für Matrizen höherer Dimension sind iterative Verfahren oft besser. Diese nähern die Lösung schrittweise an und benötigen in jedem Schritt für eine vollbesetzte Matrix ${\mathcal {O}}(n^{2})$ Rechenoperationen. Die Konvergenzgeschwindigkeit solcher Verfahren hängt stark von den Eigenschaften der Matrix ab und man kann die konkret benötigte Rechenzeit nur schwer vorhersagen.

Die Rechnung kann auf dem Speicher der Matrix $A$ durchgeführt werden, so dass außer der Speicherung von $A$ selbst kein zusätzlicher Speicherbedarf entsteht. Für eine vollbesetzte Matrix der Dimension $n=1000$ müsste man eine Million Koeffizienten abspeichern. Dies entspricht im IEEE-754-Format double in etwa 8 Megabyte. Bei iterativen Verfahren, die mit Matrix-Vektor-Multiplikationen arbeiten, kann allerdings eine explizite Speicherung von $A$ selbst nicht nötig sein, so dass diese Verfahren ggf. vorzuziehen sind.

Für Spezialfälle lassen sich Aufwand und Speicherplatz deutlich reduzieren, indem spezielle Eigenschaften der Matrix und ihrer LR-Zerlegung ausgenutzt werden können. So benötigt die Cholesky-Zerlegung für symmetrische positiv definite Matrizen nur die Hälfte an Rechenoperationen und Speicher. Ein anderes Beispiel sind Bandmatrizen mit fester Bandbreite $m$ , da hier die LR-Zerlegung die Bandstruktur erhält und sich so der Aufwand auf ${\mathcal {O}}(nm^{2})$ reduziert. Für wenige spezielle dünnbesetzte Matrizen ist es möglich, die Besetzungsstruktur auszunutzen, so dass die LR-Zerlegung ebenfalls dünnbesetzt bleibt. Beides geht einher mit einem verringerten Speicherbedarf.

Voraussetzungen der Genauigkeit – Verfahren

Damit die Berechnung von $x$ ausreichend genau ist, darf zum einen die Kondition der Matrix nicht zu schlecht und die verwendete Maschinengenauigkeit nicht zu gering sein. Zum anderen benötigt man ein Lösungsverfahren, das ausreichend stabil ist. Ein guter Algorithmus zeichnet sich also durch eine hohe Stabilität aus.

Im Allgemeinen ist das Verfahren ohne Pivotisierung instabil. Daher wird meist Spaltenpivotisierung zur Lösung verwendet. Damit ist das Verfahren für die meisten Matrizen stabil durchführbar, wie insbesondere durch die Arbeiten von James H. Wilkinson nach dem Zweiten Weltkrieg klar wurde. Es lassen sich allerdings Matrizen angeben, für welche die Stabilitätskonstante exponentiell mit der Dimension der Matrix wächst. Mit vollständiger Pivotisierung lässt sich die Stabilität noch verbessern, allerdings steigt dann auch der Aufwand für die Pivotsuche auf ${\mathcal {O}}(n^{3})$ , daher wird diese selten verwendet. Generell bessere Stabilität haben QR-Zerlegungen, die allerdings auch aufwändiger zu berechnen sind.

Bei strikt diagonaldominanten oder positiv definiten Matrizen (siehe auch Cholesky-Zerlegung) ist das Gauß-Verfahren stabil und ohne Pivotisierung durchführbar, es treten also keine Nullen auf der Diagonale auf.

Nachiteration

Ein praktischer Ansatz zum Ausgleich dieser Rechenungenauigkeiten besteht aus einer Nachiteration mittels Splitting-Verfahren, da über die LR-Zerlegung eine gute Näherung der Matrix A zur Verfügung steht, die leicht invertierbar ist. Dazu startet man mit der berechneten Lösung $x_{0}=x$ und berechnet in jedem Schritt das Residuum

r_{k}=b-Ax_{k}.

Danach berechnet man unter Verwendung der LR-Zerlegung die Lösung $z_{k}$ des Gleichungssystems

Az_{k}=r_{k}

und setzt

x_{k+1}=x_{k}+z_{k}.

Da es meistens nur um kleine Korrekturen geht, reichen oft wenige Iterationsschritte. Im Allgemeinen ist für die Berechnung des Residuums $r_{k}$ allerdings eine höhere Genauigkeit notwendig. Reicht auch die Nachiteration nicht aus, um auf die gewünschte Genauigkeit zu kommen, bleibt nur die Wahl eines anderen Verfahrens oder eine Umformung des Problems, um eine günstigere Matrix zu erhalten, etwa eine mit kleinerer Kondition.

Die Nachiteration wird beispielsweise in der LAPACK-Routine DSGESV angewandt. In dieser Routine wird die LR-Zerlegung in einfacher Genauigkeit ermittelt und die doppelte Genauigkeit der Lösung durch Nachiteration mit doppeltgenau berechnetem Residuum erreicht.

Das Gauß-Verfahren als theoretisches Hilfsmittel

Das Gauß-Verfahren ist neben seiner Bedeutung zur numerischen Behandlung von eindeutig lösbaren linearen Gleichungssystemen auch ein wichtiges Hilfsmittel in der theoretischen linearen Algebra.

Aussagen zur Lösbarkeit des linearen Gleichungssystems

Ein lineares Gleichungssystem kann keine Lösung (unlösbar), genau eine Lösung (eindeutig lösbar) oder unendlich viele Lösungen haben. Bei Verwendung von vollständiger Pivotisierung bringt das Gauß-Verfahren jede Koeffizientenmatrix auf eine reduzierte Stufenform. Der Rang der (ursprünglich gegebenen) Koeffizientenmatrix ist gleich der Anzahl der Nichtnullzeilen der in reduzierte Stufenform gebrachten Matrix. Die Lösbarkeit ergibt sich dann aus dem Zusammenspiel mit der rechten Seite: Gehören zu den Nullzeilen der in reduzierte Stufenform gebrachten Matrix Nichtnulleinträge der rechten Seite, ist das Gleichungssystem unlösbar, ansonsten lösbar. Die Anzahl der freien Parameter in der Lösungsmenge ist gleich der Anzahl der Unbekannten minus dem Rang. Das alles ergibt sich aus dem Satz von Kronecker-Capelli.

Beispiel: ${\begin{array}{rcrcl}x&+&4y&=&8,\\3x&+&12y&=&24.\end{array}}$

Da die zweite Gleichung ein Vielfaches der ersten Gleichung ist, hat das Gleichungssystem unendlich viele Lösungen. Bei der Elimination von x in der zweiten Gleichung verschwindet diese vollständig, übrig bleibt nur die erste Gleichung. Löst man diese nach x auf, kann man die Lösungsmenge in Abhängigkeit von y, der dann die Rolle eines freien Parameters spielt, angeben:

{\begin{array}{rcl}x&=&8-4y\\L&=&\{(8-4y,y)^{T}|y\}\end{array}}

Determinante

Ferner liefert das Gauß-Verfahren eine Möglichkeit, die Determinante einer Matrix zu berechnen. Da die elementaren Zeilenumformungen die Determinante 1 haben, bis auf Zeilenvertauschungen, deren Determinante −1 ist (dies ändert jedoch nur das Vorzeichen und lässt sich daher leicht korrigieren), hat die sich ergebende obere Dreiecksmatrix dieselbe Determinante wie die ursprüngliche Matrix, kann aber wesentlich einfacher berechnet werden: Sie ist das Produkt der Diagonalelemente.

Berechnung der Inversen

Eine weitere Möglichkeit der Anwendung des Gauß-Verfahrens besteht in der Berechnung der Inversen der Matrix. Hierzu wird der Algorithmus auf ein von rechts durch eine Einheitsmatrix erweitertes Schema angewandt und nach der ersten Phase fortgesetzt, bis links eine Einheitsmatrix erreicht ist. Im rechten Teil steht dann die inverse Matrix. Dieses Verfahren ist numerisch nicht zu empfehlen und die explizite Berechnung der Inversen kann meist umgangen werden.

Geschichte

Bereits im chinesischen Mathematikbuch Jiu Zhang Suanshu (dt. Neun Bücher arithmetischer Technik), das zwischen 200 vor und 100 nach Christus verfasst wurde, findet sich eine beispielhafte, aber klare Demonstration des Algorithmus anhand der Lösung eines Systems mit drei Unbekannten. 263 veröffentlichte Liu Hui einen umfassenden Kommentar zu dem Buch, der daraufhin in das Textkorpus einging. Das Jiu Zhang Suanshu war bis ins 16. Jahrhundert eine wesentliche Quelle der mathematischen Bildung in China und umliegenden Ländern.

In Europa wurde erst 1759 von Joseph-Louis Lagrange ein Verfahren publiziert, das die grundlegenden Elemente enthält. Carl Friedrich Gauß beschäftigte sich im Rahmen seiner Entwicklung und Anwendung der Methode der kleinsten Quadrate mit linearen Gleichungssystemen, den dort auftretenden Normalgleichungen. Seine erste Veröffentlichung zu dem Thema stammt von 1810 (Disquisitio de elementis ellipticis Palladis), allerdings erwähnt er bereits 1798 in seinen Tagebüchern kryptisch, er habe das Problem der Elimination gelöst. Sicher ist, dass er das Verfahren zur Berechnung der Bahn des Asteroiden Pallas zwischen 1803 und 1809 nutzte. In den 1820ern beschrieb er das erste Mal etwas wie eine LR-Zerlegung. Das Eliminationsverfahren wurde in der Folgezeit vor allem in der Geodäsie eingesetzt (siehe bei Gauß' Leistungen), und so ist der zweite Namensgeber des Gauß-Jordan-Verfahrens nicht etwa der Mathematiker Camille Jordan, sondern der Geodät Wilhelm Jordan.

Im und nach dem Zweiten Weltkrieg gewann die Untersuchung numerischer Verfahren an Bedeutung und das Gauß-Verfahren wurde nun auch vermehrt auf Probleme unabhängig von der Methode der kleinsten Quadrate angewandt. John von Neumann und Alan Turing definierten die LR-Zerlegung in der heute üblichen Form und untersuchten das Phänomen der Rundungsfehler. Befriedigend gelöst wurden diese Fragen erst in den 1960ern durch James Hardy Wilkinson, der zeigte, dass das Verfahren mit Pivotisierung rückwärtsstabil ist.

Literatur

Gerd Fischer: Lineare Algebra, Vieweg-Verlag, ISBN 3-528-97217-3.
Gene Golub und Charles van Loan: Matrix computations. 3. Auflage. Johns Hopkins University Press, Baltimore 1996, ISBN 0-8018-5414-8 (englisch).
Andrzej Kielbasiński, Hubert Schwetlick: Numerische lineare Algebra. Eine computerorientierte Einführung. Deutscher Verlag der Wissenschaften, Berlin 1988, ISBN 3-326-00194-0.
Andreas Meister: Numerik linearer Gleichungssysteme. Eine Einführung in moderne Verfahren. 2. Auflage, Vieweg, Wiesbaden 2005, ISBN 3-528-13135-7.
Martin Hermann: Numerische Mathematik, Band 1: Algebraische Probleme. 4., überarbeitete und erweiterte Auflage. Walter de Gruyter Verlag, Berlin und Boston 2020. ISBN 978-3-11-065665-7.

Weblinks

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.