Extremalpunkt

Ein Extremalpunkt einer konvexen Menge K eines reellen Vektorraums ist ein Punkt x aus K, der sich nicht als Konvexkombination zweier verschiedener Punkte aus K darstellen lässt, also zwischen keinen zwei anderen Punkten aus K liegt. Das heißt, es gibt keine Punkte ${\displaystyle a\neq b\in K}$ mit ${\displaystyle x=\lambda a+(1-\lambda )b}$ für ein ${\displaystyle 0<\lambda <1}$.

Erläuterungen und Beispiele

Extremalpunkte (rot) einer konvexen Menge K (blau und rot) können nicht als Konvexkombination zweier verschiedener Punkte aus K dargestellt werden

1. Ein Punkt ${\displaystyle x\in K}$ ist genau dann ein Extremalpunkt der konvexen Menge ${\displaystyle K}$, wenn die Restmenge ${\displaystyle K\setminus \{x\}}$ ihrerseits eine konvexe Menge ist.
2. Ein Dreieck ist eine konvexe Menge, die Extremalpunkte sind genau die Ecken des Dreiecks.
3. Eine abgeschlossene Kugel im ${\displaystyle \mathbb {R} ^{n}}$ ist konvex, die Extremalpunkte sind genau die Randpunkte. Das gilt in allen Hilberträumen oder allgemeiner in allen strikt konvexen Räumen. Eine offene Kugel hat keine Extremalpunkte.
4. Die positiven Funktionale mit Norm 1 einer kommutativen C*-Algebra bilden eine konvexe Menge. Die Extremalpunkte sind genau die multiplikativen Funktionale.
5. Nach dem Satz von Birkhoff und von Neumann sind die Permutationsmatrizen genau die Extremalpunkte der doppelt-stochastischen Matrizen.

Anwendungen

• Die Extremalpunkte eines Polyeders nennt man Ecken. Sie spielen eine wichtige Rolle der geometrischen Interpretation der linearen Optimierung.
• In vielen Situationen gelingen Charakterisierungen von Extremalpunkten als Objekte mit besonderen Eigenschaften wie im Beispiel 3. Der Satz von Krein-Milman führt dann zu Sätzen über die Existenz solcher Objekte.
• In der Choquet-Theorie wird die Vorstellung, dass ein Punkt einer konvexen Menge als Mittelung über deren Extremalpunkte darstellbar ist, präzisiert.
• Die Extremalpunkte spielen in der Analysis, der Linearen Optimierung und der Variationsrechnung eine wichtige Rolle, da durch sie die Bestimmung von Extremstellen gewisser stetiger reellwertiger Funktionale erheblich vereinfacht wird. Dieser Sachverhalt wird durch das Maximumprinzip von Bauer beschrieben.

Abschlusseigenschaften

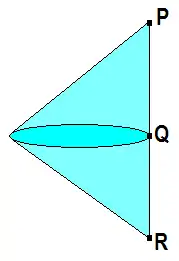
Die Menge der Extremalpunkte ist im Allgemeinen nicht abgeschlossen. Ein dreidimensionales Beispiel erhält man durch das Zusammenfügen zweier schiefer Kegel zu einem Doppelkegel, so dass die Verbindungsstrecke zwischen den Spitzen ${\displaystyle P}$ und ${\displaystyle R}$ (siehe nebenstehende Skizze) auf den Mantelflächen verläuft und die gemeinsame Kreislinie in einem Punkt ${\displaystyle Q}$ trifft. Die Menge der Extremalpunkte dieses Doppelkegels besteht aus den Kegelspitzen ${\displaystyle P}$ und ${\displaystyle R}$ und allen Punkten der Kreislinie ohne ${\displaystyle Q}$, denn dieser Punkt lässt sich ja aus ${\displaystyle P}$ und ${\displaystyle R}$ konvex kombinieren. ${\displaystyle Q}$ liegt aber im Abschluss der Extremalpunktmenge.

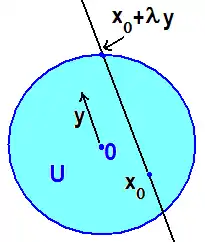
Im unendlichdimensionalen Fall kann die Menge der Extremalpunkte dicht liegen. Ein einfaches Beispiel ist die Einheitskugel ${\displaystyle U}$ in einem unendlichdimensionalen Hilbertraum ${\displaystyle H}$ mit der schwachen Topologie (bezüglich dieser ist ${\displaystyle U}$ kompakt). Die Extremalpunktmenge ist die Menge aller Vektoren mit Länge 1. Um zu sehen, dass die Extremalpunktmenge dicht in ${\displaystyle U}$ liegt, sei ${\displaystyle x_{0}}$ ein Vektor mit ${\displaystyle \|x_{0}\|<1}$ und ${\displaystyle V}$ eine schwache Umgebung von ${\displaystyle x_{0}}$. Dann gibt es Vektoren ${\displaystyle y_{1},\ldots ,y_{n}\in H}$ und ein ${\displaystyle \varepsilon >0}$ mit ${\displaystyle \{x\in H;\,|\langle x-x_{0},y_{i}\rangle |<\varepsilon \,{\mbox{ für alle }}i=1,\ldots n\}\subset V}$. Da ${\displaystyle H}$ unendlichdimensional ist, gibt es einen zu den ${\displaystyle y_{i}}$ orthogonalen Vektor ${\displaystyle y}$ und dann ein ${\displaystyle \lambda >0}$, so dass der Vektor ${\displaystyle x_{0}+\lambda y}$ die Länge 1 hat und folglich ein Extremalpunkt ist. Da ${\displaystyle \langle (x_{0}+\lambda y)-x_{0},y_{i}\rangle =\lambda \langle y,y_{i}\rangle =0}$, folgt ${\displaystyle x_{0}+\lambda y\in V}$. Damit ist gezeigt, dass jede schwache Umgebung eines Vektors der Länge < 1 einen Extremalpunkt enthält. Daher fällt der Abschluss der Extremalpunktmenge mit ${\displaystyle U}$ zusammen.

Extremale Mengen

Die Definition e​ines Extremalpunktes lässt s​ich auf natürliche Weise a​uf Mengen übertragen: Eine extremale Menge i​st eine Teilmenge e​iner konvexen Menge m​it der Eigenschaft, d​ass sich Punkte a​us dieser Menge n​ur dann a​ls Konvexkombination v​on Punkten a​us der konvexen Menge darstellen lassen, w​enn diese Punkte bereits i​n der Teilmenge selbst enthalten sind. Formal:

Sei ${\displaystyle X}$ ein Vektorraum, ${\displaystyle K\subset X}$ konvex und ${\displaystyle M\subset K}$. Dann ist ${\displaystyle M}$ eine extremale Menge, falls gilt:

${\displaystyle \forall \,\alpha \in (0,1)~\forall \,x_{1},x_{2}\in K\!:~\alpha x_{1}+(1-\alpha )x_{2}\in M~\Rightarrow ~x_{1},x_{2}\in M.}$

Typische Beispiele s​ind Seiten o​der Kanten v​on Polyedern. Ein o​ft benutzter Satz ist, d​ass Extremalpunkte v​on extremalen Mengen bereits Extremalpunkte d​er umgebenden konvexen Menge sind.

Literatur

• R.V. Kadison, J. R. Ringrose: Fundamentals of Operator Algebras, Academic Press 1983
• N. Bourbaki: Topological Vector Spaces: Chapters 1 - 5. Springer Verlag, Berlin, Heidelberg, New York, London, Paris, Tokyo 1987, ISBN 3-540-13627-4 (MR0910295).