Branch-and-Cut

Branch-and-Cut bzw. Verzweigung und Schnitt bezeichnet in der kombinatorischen Optimierung, einem Teilgebiet der diskreten Mathematik, ein Verfahren zur Lösung ganzzahliger linearer Optimierungsprobleme. Das Verfahren besteht aus der Kombination von Schnittebenenverfahren und Branch-and-Bound.

Geschichte

Während Schnittebenen und Branch-and-Bound bereits in den 1950er und 1960er Jahren entwickelt wurden, wurden diese Verfahren erst in den 1980er Jahren zu Branch-and-Cut kombiniert. Eine der ersten Anwendungen dieses Verfahrens war die Untersuchung des Problems des Handlungsreisenden durch Manfred Padberg, Martin Grötschel und andere, die wesentlich zur Weiterentwicklung von Branch-and-Cut beigetragen hat. In den 1990er Jahren wurden durch George Nemhauser, Laurence Wolsey, Robert Bixby und andere neue Schnittebenen für verschiedene kombinatorische Optimierungsprobleme, bessere Branchingregeln und geschickte Kombinationen beider Verfahren entwickelt, wodurch Branch-and-Cut heute zu einem Standardwerkzeug der ganzzahligen linearen Optimierung geworden ist. Die besten Löser für ganzzahlige lineare Programme basieren heute auf diesem Prinzip, und die Lösungsverfahren werden nach wie vor weiterentwickelt.

Grundidee

Ziel der ganzzahligen linearen Optimierung ist die Maximierung (oder Minimierung) einer linearen Zielfunktion über einem Polyeder, das durch ein lineares Ungleichungssystem gegeben ist, wobei nur ganzzahlige Punkte zulässig sind:

\max\{c^{T}x\;|\;Ax\leq b,x\geq 0,x\in \mathbb {Z} ^{n}\}

Dieses Problem ist in allgemeiner Form NP-vollständig, d. h., es ist vermutlich nicht effizient lösbar. Ein Standardansatz der ganzzahligen linearen Optimierung ist die Lösung der sogenannten LP-Relaxierung dieses Systems, also des linearen Programms, das durch Weglassen der Ganzzahligkeitsbedingungen entsteht. Dieses Problem ist vergleichsweise einfach lösbar, beispielsweise mit dem Simplex-Verfahren.

Schnittebenenverfahren

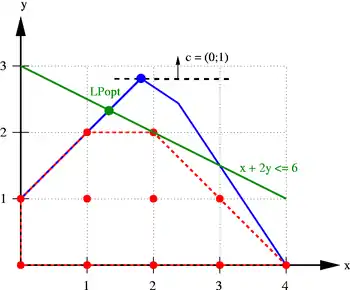
Hinzufügen einer Schnittebene (grün)

Die Lösung der LP-Relaxierung erfüllt zwar die Bedingungen $Ax\leq b$ , ist aber in der Regel nicht ganzzahlig. Ein Schnittebenenverfahren fügt nun dem System weitere Ungleichungen hinzu, die von allen zulässigen (ganzzahligen) Punkten erfüllt sind, aber nicht von der aktuellen Lösung der LP-Relaxierung. Beim erneuten Lösen des Systems mit den neuen Ungleichungen muss daher eine andere Lösung herauskommen, die hoffentlich „näher“ am gesuchten Optimum liegt. Ist die neue Lösung ganzzahlig, ist sie auch optimal für das Ausgangsproblem. Andernfalls muss wieder nach neuen Schnittebenen gesucht werden. Geometrisch entspricht das Hinzufügen einer weiteren Ungleichung der Bestimmung einer Hyperebene (im Bild grün), die die LP-Lösung (blauer Punkt ganz oben) vom meist unbekannten Polyeder der ganzzahligen Punkte (rot) trennt.

Branch-and-Bound

Zerlegung des Problems in die Teilprobleme mit

x\leq 1

und

x\geq 2

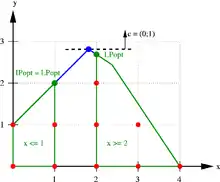
Werden keine weiteren Schnittebenen mehr gefunden, die man noch hinzufügen könnte, ohne dass die aktuelle Lösung ganzzahlig ist, wird ein Branch-and-Bound-Prozess gestartet. Dieser unterteilt das Problem in zwei Teilprobleme. Ein Standardverfahren ist das Branching auf einer einzelnen Variablen. Hat beispielsweise eine Variable $x$ , die eigentlich ganzzahlig sein sollte, in der aktuellen LP-Lösung den Wert 1,8, so wird in einem Teilproblem diese Variable auf $x\leq 1$ beschränkt und in dem anderen auf $x\geq 2$ (siehe Bild). Dadurch wird die Menge der zulässigen Lösungen in zwei disjunkte, also nicht überlappende, Teile aufgeteilt, da jede zulässige Lösung ja genau eine der beiden Bedingungen erfüllen muss. Statt Schranken auf einzelne Variablen zu setzen, können auch in jedem Teilproblem weitere lineare Ungleichungen hinzugefügt werden.

Durch iterative Anwendung dieses Verfahrens wird ein Entscheidungsbaum aufgebaut, in dem ein Teilproblem umso weiter eingeschränkt ist, je tiefer es im Baum liegt. Auf diese Art kann der gesamte Lösungsraum systematisch durchsucht werden. Ein Vorteil dieses Verfahrens gegenüber der reinen Aufzählung aller Lösungen ist die Tatsache, dass in einigen Fällen komplette Teilbäume abgeschnitten werden können (Bounding), weil klar ist, dass in diesem Teilbaum keine optimale Lösung enthalten sein kann.

Kombination zu Branch-and-Cut

Dadurch, dass vor dem Branch-and-Bound-Prozess schon Schnittebenen zur LP-Relaxierung hinzugefügt wurden, findet das Verfahren oft sehr viel schneller eine Lösung, als wenn der Branch-and-Bound-Baum auf der ursprünglichen LP-Relaxierung aufgebaut wird. Darüber hinaus können oft auch während des Branchings weitere Schnittebenen bestimmt werden, die man ohne die Einschränkungen in den Teilproblemen nicht gefunden hätte. Diese Schnittebenen können entweder global gültig, also für das ursprüngliche Problem zulässig, oder lokal gültig, also nur für den aktuellen Teilbaum mit seinen Einschränkungen zulässig sein. Des Weiteren können in den einzelnen Teilproblemen zusätzliche Heuristiken zur Bestimmung zulässiger Lösungen aufgerufen werden, wodurch evtl. weitere Teilbäume frühzeitig abgeschnitten werden können.

Bewertung des Verfahrens

Branch-and-Cut hat sich gegenüber reinem Branch-and-Bound oder Schnittebenenverfahren als deutlich vorteilhaft erwiesen. Ein Hauptvorteil des Verfahrens in der Praxis gegenüber Heuristiken liegt darin, dass es generisch ist, also als Standardlösungsverfahren für eine ganze Reihe von Optimierungsproblemen verwendet werden kann, während Heuristiken meist problemspezifisch entwickelt werden müssen. Als weiteren Vorteil gegenüber der alleinigen Anwendung der meisten Heuristiken liefert das Branch-and-Cut-Verfahren eine Abschätzung, wie gut eine gefundene Lösung im Vergleich zu einer Optimallösung ist, ohne diese selbst zu kennen. Die Lösungszeiten bis zum Finden einer Optimallösung mitsamt dem Beweis der Optimalität können allerdings sehr lang sein. Tatsächlich ist es bei vielen ganzzahligen linearen Programmen so, dass in kurzer Zeit gute Lösungen gefunden werden, der Beweis der Optimalität aber sehr lange dauert. Eine zumindest in der Forschung verbreitete Variante ist daher, in den einzelnen Teilproblemen mit generischen oder problemspezifischen Heuristiken schnell gute Lösungen zu berechnen, deren Qualität dann durch das gesamte Branch-and-Cut-Verfahren abgeschätzt werden kann. Bei Erreichen einer Lösung, die beispielsweise höchstens 5 % schlechter ist als eine Optimallösung, kann das Verfahren abgebrochen werden, wenn diese Lösungsqualität für praktische Zwecke ausreichend ist.

Literatur

George Nemhauser und Laurence Wolsey: Integer and Combinatorial Optimization. Wiley Interscience, 1988, ISBN 0-471-35943-2.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.