Optimierung (Mathematik)

Das Gebiet der Optimierung in der angewandten Mathematik beschäftigt sich damit, optimale Parameter eines – meist komplexen – Systems zu finden. „Optimal“ bedeutet, dass eine Zielfunktion minimiert oder maximiert wird. Optimierungsprobleme stellen sich in der Wirtschaftsmathematik, Statistik, Operations Research und generell in allen wissenschaftlichen Disziplinen, in denen mit unbekannten Parametern gearbeitet wird, wie beispielsweise in der Physik, der Chemie sowie der Meteorologie. Häufig ist eine analytische Lösung von Optimierungsproblemen nicht möglich und es müssen numerische Verfahren eingesetzt werden.

Beispiel einer lokalen Optimierungsaufgabe

Beispiel eines einfachen Optimierungsproblems

Das einfachste Optimierungsproblem ist das Auffinden eines Minimums oder Maximums einer differenzierbaren eindimensionalen Funktion $f(x)$ , was in der Regel durch Auffinden der Nullstellen der ersten Ableitung gelingt.

Beispiele für Optimierungsprobleme

Beispiel einer globalen Optimierungsaufgabe

Wirtschaftsmathematik: Die Zielfunktion stellt hier meist den Gewinn oder den Umsatz einer Firma dar; Parameter sind Rohstoffe, Personal-, Maschineneinsatz, Preise usw. Die Zielfunktion soll maximiert werden. Im Grunde genommen handelt es sich um eine vereinfachte Formalisierung eines grundlegenden Managementproblems. Seine systematische Fundierung erhält es in der Operations Research.
Statistik, Data-Mining: Statistische Modelle enthalten offene Parameter, die geschätzt werden. Ein Parametersatz ist optimal, wenn die zugehörige Modellinstanz die Datenbeziehungen optimal darstellt, d. h. die Abweichungen der modellierten Daten (im Sinne einer passenden Gütefunktion) von den empirischen Daten so gering wie möglich, also optimal sind. Die Zielfunktion kann hier unterschiedlich gewählt werden, zum Beispiel als Fehlerquadratsumme oder als Likelihood-Funktion.
Klimaforschung: Klimamodelle stellen vereinfachte numerische Systeme der eigentlichen hydrodynamischen Prozesse in der Atmosphäre dar. Innerhalb der Gitterzellen müssen die Wechselwirkungen durch Gleichungen approximiert werden. Die Gleichungen können dabei entweder aus grundlegenden hydrodynamischen Gesetzen abgeleitet werden oder es werden empirische Gleichungen verwendet, also im Grunde statistische Modelle, deren Parameter so optimiert werden müssen, dass die Klimamodelle die tatsächlichen Prozesse möglichst gut darstellen.
Spieltheorie: Erreicht eine Spielerpopulation in einem Superspiel ein Populationsoptimum? Oder wenigstens ein Pareto-Optimum? Ist dieses Gleichgewicht stabil?
Physik: Auswertung von Messkurven, indem Parameterwerte einer Theoriefunktion so variiert werden („Optimierung im Parameterraum“, s. a. Ausgleichsrechnung („Fitten“)), dass die Theoriefunktion bestmöglich mit der Messkurve übereinstimmt. Physikalische Systeme streben stets ein Energie-Minimum an; viele Problemstellungen bestehen gerade darin, dieses Energie-Minimum zu finden.

Abgrenzung

Verwandt mit der Optimierung ist das Gebiet der Approximation in der Numerik. Man kann umgekehrt sagen: Ein Approximationsproblem ist das Problem, den Abstand (die Metrik) zweier Funktionen zu minimieren.

Begriffe: Zielfunktion, Nebenbedingungen, zulässige Menge, lokale und globale Optimierung

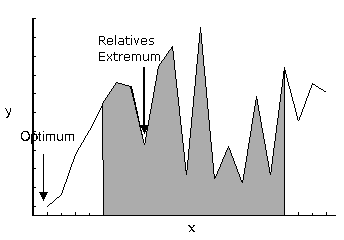
Es sei im Folgenden eine Minimierungsaufgabe angenommen. Das, was optimiert werden soll, zum Beispiel ein Abstand, nennt man Zielfunktion. Das, was variiert wird, sind die Parameter oder Variablen der Zielfunktion. Bei einer zweidimensionalen Optimierungsaufgabe (also zwei unabhängige Parameter) kann man sich die Zielfunktion räumlich vorstellen, indem die Parameter die Längen- und Tiefenachse aufspannen. Die Höhe ist dann der Zielfunktionswert. In der reinen Anschauung entsteht so (zumindest bei stetigen Funktionen) ein „Gebirge“ mit Bergen und Tälern.

Falls es sich bei der Optimierungsaufgabe tatsächlich um ein Approximationsproblem handelt, dann spricht man bei dem „Gebirge“ mitunter auch von der Fittopologie. In diesem Fall wird als Zielfunktion in den allermeisten Fällen die Fehlerquadratsumme eingesetzt, siehe Details im Artikel Methode der kleinsten Quadrate.

Da die Zielfunktion ein „Gebirge“ darstellt, ist das Optimierungsproblem damit gleichzusetzen, in diesem Gebirge das tiefste Tal (Minimierung) oder den höchsten Gipfel (Maximum) zu finden. Der Aufwand zur Lösung der Aufgabe hängt entscheidend von der Form des „Gebirges“ ab. Extrembeispiel für eine Minimierungsaufgabe wäre eine absolut flache Ebene, aus der an zufälligen Punkten einzelne nadelförmige Spitzen herausragen. In diesem Fall hilft keinerlei Suchalgorithmus, man kann nur zufällig suchen (Monte-Carlo-Methode) oder systematisch die gesamte Fläche abrastern. Einer der einfachsten Fälle einer zweidimensionalen Optimierungsaufgabe liegt vor, wenn das Gebirge die Form einer um die Höhenachse symmetrischen Parabel hat, deren Scheitelpunkt zu finden ist.

Besteht die Optimierungsaufgabe darin, von einem gegebenen Punkt im Gebirge aus das nächste relative (lokale) Minimum oder Maximum in der Nachbarschaft zu finden, dann spricht man von lokaler Optimierung. Besteht die Aufgabe darin, das absolute Minimum oder Maximum im gesamten Gebirge zu finden, dann spricht man von globaler Optimierung. Die beiden Aufgaben haben einen stark unterschiedlichen Schwierigkeitsgrad: Für die lokale Optimierung gibt es zahlreiche Methoden, die alle mehr oder weniger schnell in allen nicht allzu schwierigen Fällen mit großer Sicherheit zum Ziel führen. Bei der globalen Optimierung hängt die Lösbarkeit der Aufgabe im Rahmen eines gegebenen oder realisierbaren Rechenbudgets sehr stark von der Zielfunktionstopologie ab.

Häufig ist man nur an solchen Werten für die Parameter interessiert, die zusätzliche Nebenbedingungen (NB) erfüllen. (Gelten diese Nebenbedingungen nur am Rande des Definitionsbereichs der Funktion, heißen sie auch Randbedingungen.) Sie können in Form von Gleichungen oder Ungleichungen gegeben sein, oder explizit eine Menge beschreiben (zum Beispiel nur ganzzahlige Lösungen). Die Menge aller Parameterwerte, die alle NB erfüllen, bezeichnet man als zulässige Menge. Bei dem Gebirge würden die NB das Gebiet, in dem gesucht wird, eingrenzen. Das betrachtete Optimierungsproblem nennt man zulässig, wenn die zulässige Menge, also das abzusuchende Gebiet, nicht leer ist. Man unterscheidet aktive und passive Nebenbedingungen: Eine NB der Form $g(x)\leq 0$ ist aktiv, wenn das Optimum auf dem Rand des zulässigen Bereiches liegt und daher Gleichheit $g(x)=0$ vorliegt. Wäre die NB passiv, würde sie im Optimum keine Einschränkung darstellen, das Optimum liegt also im Gebiet und nicht auf dem Rand. Eine NB der Form $h(x)=0$ ist immer aktiv.

Klassifikation

Skalare Optimierungsprobleme

Ein skalares Optimierungsproblem lässt sich mathematisch als

„Minimiere/maximiere

f(x)

unter der Nebenbedingung

x\in X

“

darstellen; hierbei ist $f\colon V\to \mathbb {R}$ eine reellwertige Funktion und $X\subseteq V$ . Häufig ist die zulässige Menge $X$ indirekt durch eine Funktion gegeben, gewöhnlich standardisiert in der Form

X=\{x\in V:g(x)\leq 0\}

mit einer vektorwertigen Funktion

g\colon V\to \mathbb {R} ^{m}

(der Vergleich bedeutet: keine Komponente von

g(x)

darf positiv sein).

Je nach Form von $V,X,f,g$ lassen sich skalare Optimierungsprobleme wie folgt klassifizieren:

Variationsproblem: $V$ ist unendlichdimensional, speziell ein Funktionenraum.
Optimales Steuerungsproblem: Klassisches Variationsproblem mit Differentialgleichungsnebenbedingung
Lineares Programm (LP): $V=\mathbb {R} ^{n},g=Ax-b$ wobei $A\in \mathbb {R} ^{m\times n}$ ist affin, $f=c^{T}x$ ist linear.
Quadratisches Programm (QP): wie oben, nur ist $f$ eine quadratische Funktion.
Quadratisches Programm mit quadratischen Nebenbedingungen (QCQP)
Nichtlineares Programm: $f,g$ sind beliebige Funktionen (meist stetig differenzierbar angenommen; in der engeren Umgebung eines Optimums kann oft eine quadratische Näherung verwendet werden, was zu einigen der praktischen Verfahren führt.)
Ganzzahliges Programm (auch diskretes Programm): Zusätzlich sind die zulässigen $x$ auf ganzzahlige oder allgemeiner diskrete Werte beschränkt.
Stochastisches Programm: Einige Parameter in der Beschreibung von $f,g$ sind unbekannt (aber ihre Zufallsverteilung ist bekannt).
Konvexes Programm: $X$ $\text{[math]}$ ist konvex und $f$ $\text{[math]}$ ist konvex (konkav), falls minimiert (maximiert) wird. Konvexe Programme enthalten als Spezialfall
- Konische Programme: Es werden verallgemeinerte Ungleichungen verwendet, ansonsten sind alle Funktionen affin. Konische Programme haben wiederum drei Teilgebiete:
  - Semidefinite Programme verwenden den Kegel der positiv semidefiniten Matrizen, haben also als Variable eine Matrix.
  - Die SOCPs (Second Order Cone Program) verwenden den second-order cone, der auch Lorentz-Kegel genannt wird.
  - Auch lineare Optimierungsprobleme lassen sich als konische Programme formulieren.
- Unter gewissen Voraussetzungen fallen auch Quadratische Programme und Quadratische Programme mit quadratischen Nebenbedingungen unter die konvexe Optimierung.
- Geometrische Programme sind an sich nicht konvex, lassen sich aber in ein konvexes Problem überführen.

Jedes dieser Teilgebiete der Optimierung hat speziell auf die Struktur des Problems abgestimmte Lösungsverfahren.

Hinweis zur Terminologie: „Programm“ ist als Synonym zu „Optimierungsproblem“ zu verstehen (und nicht als „Computerprogramm“). Die Verwendung des Begriffes „Programm“ ist historisch begründet: Die ersten Anwendungen der Optimierung waren militärische Probleme, bei denen ein Aktionsplan (engl.: program of actions) zu finden war.[1]

Vektoroptimierungsprobleme

Ein Optimierungsproblem aus der Vektoroptimierung (auch Pareto-Optimierung genannt) ist dagegen ein Problem, bei dem die Werte mehrerer Zielfunktionen gleichzeitig zu optimieren sind. Dies lässt sich formalisieren, indem eine vektorwertige Zielfunktion $f\colon V\to \mathbb {R} ^{n}$ optimiert wird. Lösungen, die alle Komponenten der Zielfunktion gleichzeitig zu einem Optimum führen, sind in der Regel nicht vorhanden; vielmehr ergibt sich im Allgemeinen eine größere Lösungsmenge, aus der zum Beispiel durch eine Skalarisierung (Gewichtung der Einzelkomponenten der Zielfunktion) ein einzelner Optimalpunkt selektiert werden kann.

Lineare und ganzzahlige Optimierung

Ein wichtiger Spezialfall ist die lineare Optimierung. Hierbei ist die Zielfunktion linear, und die Nebenbedingungen sind durch ein System linearer Gleichungen und Ungleichungen darstellbar. Jedes lokale Optimum ist automatisch auch globales Optimum, da der zulässige Bereich konvex ist. Es gibt Pivotverfahren, um das globale Optimum im Prinzip exakt zu berechnen, wovon die bekanntesten die Simplex-Verfahren sind (nicht zu verwechseln mit dem Downhill-Simplex-Verfahren weiter unten). Seit den 1990er Jahren gibt es allerdings auch effiziente Innere-Punkte-Verfahren, die bei bestimmten Arten von Optimierungsproblemen konkurrenzfähig zum Simplex-Verfahren sein können.

Eine Beschränkung auf ganzzahlige Variablen macht das Problem deutlich schwerer, erweitert aber gleichzeitig die Anwendungsmöglichkeiten. Diese sogenannte ganzzahlige lineare Optimierung wird beispielsweise in der Produktionsplanung, im Scheduling, in der Tourenplanung oder in der Planung von Telekommunikations- oder Verkehrsnetzen eingesetzt.

Nichtlineare Optimierung

Methoden der lokalen nichtlinearen Optimierung mit Nebenbedingungen

Schwieriger als die lineare Optimierung ist der Fall der nichtlinearen Optimierung, bei der die Zielfunktion, die Nebenbedingungen (NB) oder beide nichtlinear vorliegen. Die Lösung wird erreicht, indem das Problem auf die Optimierung einer Hilfsfunktion ohne NB zurückgeführt wird. Auf dieses neue Problem können dann die Methoden der nichtlinearen Optimierung ohne NB unten angewendet werden. Das Vorgehen soll anhand eines Kontaktproblems erläutert werden: Zwei Kugeln in einer Mulde versuchen den tiefstmöglichen Punkt einzunehmen, dürfen sich dabei aber nicht durchdringen. Die Zielfunktion ist also die Lageenergie der Kugeln und nimmt im Gleichgewicht ein Minimum an. Die Nebenbedingung $g(x,y)\leq 0$ würde hier die Durchdringung der Kugeln $x$ und $y$ bezeichnen, wobei mit negativer Durchdringung ein positiver Abstand gemeint wird. Für die Konstruktion der Hilfsfunktion liegen fünf Methoden vor:

Lagrange-Multiplikatoren: Die NB werden mit reellen Faktoren, den Lagrange-Multiplikatoren, multipliziert und zur Zielfunktion hinzuaddiert. Die Faktoren werden als Unbekannte in das Problem eingeführt und müssen (unter Einhaltung der Karush-Kuhn-Tucker-Bedingungen) ebenfalls bestimmt werden. Bei den Kugeln sind die Lagrange-Multiplikatoren gerade die Kontaktkräfte, die die Kugeln bei Berührung aufeinander ausüben, so dass sie sich nicht durchdringen.
Straffunktionen: Die NB werden mit Straffunktionen dargestellt, die im Definitionsbereich verschwinden und bei Verletzung der NB negativ sind. Die Straffunktionen werden mit Strafparametern multipliziert und zur Zielfunktion addiert (bei Maximierung, ansonsten Subtraktion), so dass die Verletzung der NB also bestraft wird, daher der Name. Hier werden aktive NB evtl. verletzt und die Zulässigkeit der Lösung muss geprüft werden. Im Kugel-Bild entspricht die Straffunktion der echten Durchdringung $\min(0,g(x,y))$ , die also bei positivem Abstand verschwindet, und der Strafparameter entspricht einer Federsteifigkeit. Die Feder versucht eindringende Punkte wieder an die Oberfläche zu ziehen. Je steifer die Feder ausfällt, desto geringer wird die Eindringung sein.
Barrierefunktionen: Die Barrierefunktionen werden wie die Straffunktionen eingesetzt. Allerdings haben sie bereits bei Annäherung an die Grenze des Definitionsbereiches negative Werte und wachsen auf der Grenze ins Unendliche. Im Kugelbild bekämen die Kugeln einen mehr oder weniger dicken Mantel, der immer steifer wird, je stärker er bei Berührung zusammengedrückt wird. Eine Verletzung der NB wird so verhindert zu dem Preis, dass bereits die Annäherung an den Rand bestraft wird.
Erweiterte Lagrange-Methode (engl. augmented lagrange method): Dies ist eine Kombination der vorhergehenden Methoden. Der Lagrange-Multiplikator wird iterativ anhand der Verletzung der NB bestimmt.
Trivial, aber doch zu erwähnen ist, dass aktive NB dazu genutzt werden können, Parameter der Zielfunktion zu eliminieren. Die Parameter werden auf Werte festgelegt, derart dass eine Verletzung der NB nunmehr unmöglich ist. Im Kugel-Bild würde man Berührungspunkte der Kugeln aneinanderkoppeln (ihre Koordinaten gleichsetzen), so dass eine Durchdringung (dort) nicht mehr stattfinden kann.

Methoden der lokalen nichtlinearen Optimierung ohne Nebenbedingungen

Bei der lokalen Optimierung hängt die Wahl der Methode von der genauen Problemstellung ab: Handelt es sich um eine beliebig exakt bestimmte Zielfunktion? (Das ist bei stochastischen Zielfunktionen oft nicht der Fall.) Ist die Zielfunktion in der Umgebung streng monoton, nur monoton oder könnte es „unterwegs“ sogar kleine relative Extrema geben? Wie hoch sind die Kosten, einen Gradienten zu bestimmen?

Beispiele für Methoden:

Ableitungsfreie Methoden

Intervallhalbierungsverfahren, Verfahren des goldenen Schnitts und andere Verfahren zur Optimierung eindimensionaler Funktionen oder zur Liniensuche (sequentiellen Suche) bei mehrdimensionalen Funktionen.
Downhill-Simplex-Verfahren
Trust-Region-Verfahren

Diese Methoden kosten viele Iterationen, sind aber (teilweise) relativ robust gegenüber Problemen in der Zielfunktion, zum Beispiel kleine relative Extrema und sie verlangen nicht die Berechnung eines Gradienten. Letzteres kann sehr kostspielig sein, wenn lediglich ein relativ ungenaues Ergebnis angestrebt wird.

Verfahren, für die die 1. Ableitung benötigt wird

Sekantenverfahren (zum Bestimmen der Nullstelle der 1. Ableitung)
Gradientenverfahren und Konjugierte-Gradienten-Verfahren.
Quasi-Newton-Verfahren

Diese Methoden sind schneller als die ableitungsfreien Methoden, sofern ein Gradient schnell berechnet werden kann, und sie sind ähnlich robust wie die ableitungsfreien Methoden.

Verfahren, für die die 2. Ableitung benötigt wird

Newton-Verfahren, bzw. Newton-Raphson-Verfahren.

Gemeinhin ist das Newton-Verfahren als Verfahren zur Bestimmung einer Nullstelle bekannt und benötigt die erste Ableitung. Dementsprechend lässt es sich auch auf die Ableitung einer Zielfunktion anwenden, da die Optimierungsaufgabe auf die Bestimmung der Nullstellen der 1. Ableitung hinausläuft. Das Newton-Verfahren ist sehr schnell, aber sehr wenig robust. Wenn man sich der „Gutartigkeit“ seines Optimierungsproblems nicht sicher ist, muss man zusätzlich Globalisierungsstrategien wie Schrittweitensuche oder Trust-Region-Verfahren verwenden.

Für die in der Praxis häufig auftretenden Probleme, in denen die zu minimierende Zielfunktion die spezielle Gestalt des Normquadrates einer vektorwertigen Funktion hat (Methode der kleinsten Quadrate, „least squares“), steht das Gauß-Newton-Verfahren zur Verfügung, das sich im Prinzip zu Nutze macht, dass für Funktionen dieser Form unter bestimmten Zusatzannahmen die teure 2. Ableitung (Hesse-Matrix) sehr gut ohne ihre explizite Berechnung als Funktion der Jacobi-Matrix angenähert werden kann. So wird in Zielnähe eine dem Newton-Verfahren ähnliche super-lineare Konvergenzgeschwindigkeit erreicht. Da dieses Verfahren die Stabilitätsprobleme des Newton-Verfahrens geerbt hat, sind auch hier sog. Globalisierungs- und Stabilisierungsstrategien erforderlich, um die Konvergenz zumindest zum nächsten lokalen Minimum garantieren zu können. Eine populäre Variante ist hier der Levenberg-Marquardt-Algorithmus.

Methoden der globalen nichtlinearen Optimierung

Im Gegensatz zur lokalen Optimierung ist die globale Optimierung ein quasi ungelöstes Problem der Mathematik: Es gibt praktisch keinerlei Methoden, bei deren Anwendung man in den meisten Fällen als Ergebnis einen Punkt erhält, der mit Sicherheit oder auch nur großer Wahrscheinlichkeit das absolute Extremum darstellt.

Allen Methoden zur globalen Optimierung gemein ist, dass sie wiederholt nach einem bestimmten System lokale Minima/Maxima aufsuchen.

Am häufigsten werden hier Evolutionäre Algorithmen angewandt. Diese liefern besonders dann ein gutes Ergebnis, wenn die Anordnung der relativen Minima und Maxima eine gewisse Gesetzmäßigkeit aufweisen, deren Kenntnis vererbt werden kann. Eine ganz gute Methode kann auch sein, die Ausgangspunkte für die Suche nach lokalen Minima/Maxima zufällig zu wählen, um dann mittels statistischer Methoden die Suchergebnisse nach Regelmäßigkeiten zu untersuchen.

Oft wird allerdings in der Praxis das eigentliche Suchkriterium nicht genügend reflektiert. So ist es oft viel wichtiger, nicht das globale Optimum zu finden, sondern ein Parametergebiet, innerhalb dessen sich möglichst viele relative Minima befinden. Hier eignen sich dann Methoden der Clusteranalyse oder neuronale Netze.

Weitere Methoden der nichtlinearen globalen Optimierung:

Naturanaloge Optimierungsverfahren
- Sintflutalgorithmus (great deluge algorithm)
- Simulierte Abkühlung (simulated annealing)
- Metropolisalgorithmus
- Schwellenakzeptanz (threshold accepting)
- Ameisenalgorithmus (ant colony optimization)
- Partikelschwarmoptimierung
Sonstige Verfahren
- Bergsteigeralgorithmus (hill climbing)
- Stochastisches Tunneln (Stochastic tunneling)
- RANSAC-Algorithmus zur besseren Handhabung von Messdaten mit Ausreißern
- Primal-Dual-Active-Set-Algorithmus zur Lösung eines quadratischen Optimierungsproblems über einer konvexen Teilmenge $S$ eines Hilbertraumes $V$ über der Menge $\Omega$

Die Performance von Optimierungsalgorithmen wird oft anhand von Testproblemen mit komplexer Struktur der Minima oder Maxima analysiert, bei denen die exakte Lösung bekannt ist. Ein Beispiel für eine solche Testfunktion ist die Rastrigin-Funktion.

Theoretische Aussagen

Bei der Optimierung einer (differenzierbaren) Funktion $f(x)$ ohne Nebenbedingungen ist bekannt, dass Minima/Maxima nur an Stellen mit $\nabla f(x)=0$ sein können. Diese Bedingung wird bei der Konstruktion vieler Lösungsverfahren ausgenutzt. In dem Fall der Optimierung mit Nebenbedingungen gibt es analoge theoretische Aussagen: Dualität und Lagrange-Multiplikatoren.

Konvexe Probleme

Bei konvexen Problemen ist das abzusuchende Gebiet und die Zielfunktion konvex. Bei einem konvexen Gebiet liegen alle Punkte auf der Verbindungslinie zweier beliebiger Punkte im Gebiet ebenfalls vollständig im Gebiet. Mathematisch:

\lambda \in [0,1]\Rightarrow x+\lambda (y-x)\in X\quad \forall x,y\in X

Beispiele für konvexe Gebiete sind Kreise, Ellipsen, Dreiecke und Quadrate.

Die Zielfunktion ist konvex, wenn alle Werte der Zielfunktion von Punkten auf der Geraden, die zwei Punkte im Gebiet verbinden, unter dieser Geraden liegen. Mathematisch:

\lambda \in [0,1]\Rightarrow f(x+\lambda (y-x))\leq f(x)+\lambda (f(y)-f(x))\quad \forall x,y\in X

.

Die zu Beginn dieses Artikels gezeigte parabelförmige Optimierungsaufgabe hat eine konvexe Zielfunktion.

Bei konvexen Problemen ist jedes lokale Minimum auch globales Minimum. Sind die Punkte $x_{i}\,,\;i=1,\dotsc ,n$ optimal, dann sind alle Punkte „zwischen“ diesen Punkten optimal. Mathematisch:

\alpha _{1},\alpha _{2},\dotsc ,\alpha _{n}\in [0,1]\;\wedge \;\sum _{i=1}^{n}\alpha _{i}=1\quad \Rightarrow \quad f\left(\sum _{i=1}^{n}\alpha _{i}x_{i}\right)=f_{\text{opt}}

.

Dualität

Das einem Optimierungsproblem $\min \;f(x):\;g(x)=0$ zugeordnete (Lagrange-)duale Problem ist

\max _{\lambda }\min _{x}{\mathcal {L}}(x,\lambda )

wobei ${\mathcal {L}}(x,\lambda )=f(x)+\lambda ^{T}g(x)$ die zugehörige Lagrange-Funktion ist. Die $\lambda$ heißen hierbei Lagrange-Multiplikatoren, oder auch duale Variablen oder Schattenpreise. Anschaulich erlaubt man eine Verletzung der Nebenbedingungen, bestraft sie aber in der Zielfunktion durch Zusatzkosten $\lambda$ pro verletzter Einheit. Eine Lösung $\lambda$ , für die es sich nicht lohnt, die Nebenbedingungen zu verletzen, löst das duale Problem. Für konvexe (insbesondere lineare) Probleme ist der Wert des dualen Problems gleich dem Wert des Ursprungsproblems. Für lineare und konvexe quadratische Probleme lässt sich die innere Minimierung geschlossen lösen und das duale Problem ist wieder ein lineares oder konvexes quadratisches Problem.

Lagrange-Multiplikatoren

Der Lagrange-Multiplikatorsatz besagt, dass Lösungen des eingeschränkten Optimierungsproblems $\min _{x}\,f(x):\,g(x)=0$ nur an Stellen $x$ zu finden sind, an denen es Lagrange-Multiplikatoren $\lambda _{i}$ gibt, die die Bedingung

\nabla _{x}{\mathcal {L}}(x,\lambda )=\nabla f(x)+\sum _{i}\lambda _{i}\nabla g_{i}(x)=0

erfüllen. Diese Bedingung ist die direkte Verallgemeinerung der obigen Ableitungsbedingung. Wie diese gibt der Lagrange-Multiplikatorensatz eine notwendige Bedingung für ein Minimum bzw. Maximum. Eine hinreichende Bedingung kann durch Betrachtung der zweiten Ableitungen gewonnen werden.

Der Lagrange-Multiplikatorensatz gilt nur für den Fall, dass die Nebenbedingungen durch Gleichungen gegeben sind. Die Verallgemeinerung auf Ungleichungen $\min _{x}\{f(x):g(x)\leq 0\}$ gibt der Satz von Karush-Kuhn-Tucker.

Straffunktionen

Im Grenzwert der gegen unendlich gehenden Strafparameter geht die mit Straffunktionen gefundene Lösung in die mit den Lagrange-Multiplikatoren gefundene Lösung über.

Erweiterte Lagrange-Methode

Im Grenzwert unendlich vieler Iterationen strebt die mit der erweiterten Lagrange-Methode gefundene Lösung auch gegen die mit den Lagrange-Multiplikatoren gefundene Lösung.

Einzelnachweise

Father of linear programming (Memento vom 11. November 2009 im Internet Archive) In: informs.org

Literatur

Walter Alt: Nichtlineare Optimierung – Eine Einführung in Theorie, Verfahren und Anwendungen. Vieweg, 2002, ISBN 3-528-03193-X.
Yonathan Bard: Nonlinear Parameter Estimation. Academic Press, New York 1974, ISBN 0-12-078250-2.
Hans Benker: Mathematische Optimierung mit Computeralgebrasystemen. Springer-Verlag, Berlin/ Heidelberg/ New York 2003.
S. Boyd, L. Vandenberghe: Convex Optimization. Cambridge University Press, 2004. (online)
W. Domschke, A. Drexl: Einführung in Operations Research. 7. Auflage. Springer, Berlin 2007, ISBN 978-3-540-70948-0.
R. Fletcher: Practical Methods of Optimization. Wiley, 1987, ISBN 0-471-91547-5.
U. Hoffmann, H. Hofmann: Einführung in die Optimierung: mit Anwendungsbeispielen aus dem Chemie-Ingenieur-Wesen. Verlag Chemie, Weinheim 1971, ISBN 3-527-25340-8.
R. Horst, P. M. Pardalos (Hrsg.): Handbook of Global Optimization. Kluwer, Dordrecht 1995, ISBN 0-7923-3120-6.
F. Jarre, J. Stoer: Optimierung. Springer, 2004, ISBN 3-540-43575-1. eingeschränkte Vorschau in der Google-Buchsuche
J. Nocedal, S. J. Wright: Numerical Optimization. Springer, Berlin 1999, ISBN 0-387-98793-2.
C. Geiger, C. Kanzow: Theorie und Numerik restringierter Optimierungsaufgaben. Springer, 2002, ISBN 3-540-42790-2. eingeschränkte Vorschau in der Google-Buchsuche
C. Grossmann, J. Terno: Numerik der Optimierung. Teubner Studienbücher, 1997, ISBN 3-519-12090-9. eingeschränkte Vorschau in der Google-Buchsuche

Weblinks

Commons: Optimization – Sammlung von Bildern, Videos und Audiodateien

Literatur zur Optimierung im Katalog der Deutschen Nationalbibliothek
Allgemeine Link-Seite zur globalen Optimierung (engl.)
Einführung in die numerische Optimierung
NEOS Optimization Guide (engl.)
Entscheidungsbaum für Optimierungssoftware (engl.)
Global Optimization Algorithms - Theory and Application (engl.; PDF-Datei; 13,14 MB)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Father of linear programming (Memento vom 11. November 2009 im Internet Archive) In: informs.org