Molekülorbitaltheorie

Die Molekülorbitaltheorie (kurz MO-Theorie) ist neben der Valenzbindungstheorie (VB-Theorie) eine von zwei komplementären Möglichkeiten, die Elektronenstruktur von Molekülen zu beschreiben. Beim MO-Verfahren werden über das Molekül delokalisierte Molekülorbitale durch eine Linearkombination der Atomorbitale aller Atome eines Moleküls gebildet. Dabei wird zwischen bindenden und antibindenden Molekülorbitalen unterschieden.[1] Das Verfahren wurde (etwas später als das VB-Verfahren) von Friedrich Hund und Robert S. Mulliken entwickelt und wird heute für die meisten quantenchemischen Rechnungen verwendet.

Physikalische Erklärung

Eine zeitunabhängige $n$ -Elektronen-Wellenfunktion hat, wenn der Spin nicht beachtet wird, die allgemeine Form $\Psi ({\vec {r}}_{1},\ldots {\vec {r}}_{n})$ . Das Produkt mit der komplex konjugierten Funktion $\Psi ^{*}({\vec {r}}_{1},\ldots {\vec {r}}_{n})\cdot \Psi ({\vec {r}}_{1},\ldots {\vec {r}}_{n})$ ist reell und gibt die Wahrscheinlichkeitsdichte wieder, das erste Elektron an der Stelle ${\vec {r}}_{1}$ , das 2-te an der Stelle ${\vec {r}}_{2}$ usw. zu finden.

Die exakte Wellenfunktion lässt sich für Mehrelektronensysteme analytisch nicht finden. Eine zielführende Vereinfachung ist es, die Elektronen als stochastisch unabhängig anzusehen. Mathematisch bedeutet das, einen Produktansatz zu verwenden $\Psi ({\vec {r}}_{1},\ldots {\vec {r}}_{n})=\prod _{i=1}^{n}\Psi _{i}({\vec {r}}_{i})$ . Dieser Ansatz ist auch als Hartree-Produkt bekannt. Die $\Psi _{i}({\vec {r}}_{i})$ geben die Aufenthaltsbereiche für die einzelnen Elektronen an. Sie werden als Molekülorbitale bezeichnet. Um das Pauli-Prinzip einzuhalten, wird die Wellenfunktion als Slater-Determinante (ein antisymmetrisierter Produktansatz) angesetzt. Dabei ist gewährleistet, dass die Wellenfunktion antisymmetrisch unter Vertauschung zweier ununterscheidbarer Elektronen ist, wie es für Fermionen gelten muss.

Abgesehen davon, dass MO-Schemata eine vereinfachte, modellhafte Beschreibung darstellen, ist zu beachten, dass sie in der MO-Theorie nicht eindeutig bestimmt sind. Entscheidend ist nur die Summe über alle quadrierten Orbitale, die Elektronendichte (das ist auch die Grundlage für die Dichtefunktionaltheorie). Mathematisch gesprochen ist die Wellenfunktion gegenüber einer unitären Lineartransformation invariant. So lassen sich neben den oft als kanonische MOs bezeichneten Orbitale verschieden andere Darstellungen finden, z. B. Localized Molecular Orbitals (LMOs).[2]

Mathematische Grundlagen

Gesucht werden Lösungen der zeitunabhängigen Schrödinger-Gleichung eines Moleküls. Die Rechnungen sind aber wesentlich schwieriger auszuführen als bei einem isolierten Atom. Im Normalfall, wenn mehr als ein Elektron betrachtet wird, gibt es im Sinne eines Dreikörperproblems keine analytisch angebbaren exakten Lösungen. Daher müssen Näherungsmethoden herangezogen werden. Dafür eignen sich das VB- und das MO-Verfahren, die zu ähnlichen Ergebnissen führen.

Wichtig ist die Born-Oppenheimer-Näherung, nach der die Elektronen- und Kernbewegung näherungsweise entkoppelt betrachtet werden können. Vereinfacht ausgedrückt, ist die in der Tatsache begründet, dass sich die Elektronen im Vergleich zum Kern viel schneller bewegen. Somit können Elektronenverteilung und Schwingung getrennt behandelt werden.

Zur näherungsweisen Bestimmung der Molekülorbitale dient das Rayleigh-Ritz-Prinzip. Das besagt, dass, wenn man mit einer beliebigen Funktion den Erwartungswert des Hamiltonoperators bildet, der Erwartungswert größer gleich dem Erwartungswert der Eigenfunktion des Hamiltonoperators mit dem geringsten Eigenwert ist. Man muss also in einer Extremwertaufgabe die Funktion mit dem tiefsten Energieerwartungswert auswählen. Diese ist dann wahrscheinlich die beste Näherung.

Einfach einen vollständigen Satz von Basisfunktionen auszuwählen, den Erwartungswert für eine allgemeine lineare Kombination dieser zu bilden und anschließend den Erwartungswert zu minimieren ist eine zu komplizierte Aufgabe. Man reduziert zur Vereinfachung des Problems das nach Born-Oppenheimer-Näherung erhaltene Mehrelektronenproblem auf ein Einelektronenproblem. Eine Möglichkeit hierfür ist die Hartree-Fock-Self-Consistent-Field-Methode, die, da es sich um ein nichtlineares Problem handelt, iterativ gelöst werden muss. Die Lösungen dieser Gleichung sind Einelektronenwellenfunktionen, sogenannte Orbitale. Das Prinzip ist, dass auf jedes Elektron das gemittelte Potential aller anderen Elektronen wirkt. Die anderen Elektronen wiederum befinden sich in den Orbitalen, die die Hartree-Fock-Gleichung beschreibt, weshalb man die Methode auch Self-Consistent-Field-Methode nennt.

MO-Verfahren

MO-Verfahren (von engl. molecular orbital) nach Friedrich Hund und Robert Sanderson Mulliken ordnen alle Elektronen des Moleküls einem Satz Molekülorbitalen zu. Die Orbitale können durch Darstellung ihrer Isoflächen veranschaulicht werden. Die Visualisierung erinnert dann mitunter an Elektronenwolken.

Molekülorbitale können als Linearkombinationen zu einer endlichen Basis angesetzt werden. Dann werden in einem erweiterten Eigenwertproblem die Molekülorbitale bestimmt. Als Basis können, wie von Lennard-Jones vorgeschlagen, die Atomorbitale der isolierten Atome im Sinne der LCAO-Näherung (von engl. Linear Combination of Atomic Orbitals) verwendet werden.

Grundsätzlich könnten beliebige Funktionen als Basis herangezogen werden. Gute Lösungen mit wenig Rechenaufwand werden erhalten, wenn physikalisch sinnvolle Funktionen verwendet werden. Dafür eignen sich, wie Lennard-Jones als erster feststellte, die Atomorbitale, die in isolierten Atomen die Elektronen richtig beschreiben. Man spricht dann von LCAO. Zur Verbesserung können auch die Atomorbitale variiert oder weitere Funktionen in den Basissatz eingeschlossen werden.

MO-Verfahren können bei kleinen symmetrischen Molekülen intuitiv verstanden werden. Aus Symmetriegründen ergeben sich die Molekülorbitale aus Addition bzw. Subtraktion der Atomorbitale. Bei konjugierten π-Systemen stellt die Hückel-Näherung eine Methode zur groben Bestimmung von π-MOs dar.

Das einfachste allgemeine MO-Verfahren ist die Hartree-Fock-Methode (HF). Ein grundsätzlicher Fehler dieser Methode ist, dass die Elektronen (bis auf Einhaltung des Pauli-Prinzips) als statistisch unabhängig voneinander gesehen werden. Auf der HF-Methode aufbauende korrelierte Rechnungen, v. a. CI (engl. für configuration interaction), beachten auch die Elektronen-Korrelation.

Zeichnen von LCAO-MO-Diagrammen

Qualitative LCAO-MO-Diagramme können auch ohne Rechnung gezeichnet werden. Zu beachten ist, dass bei der Linearkombination zweier AOs ein bindendes MO mit tieferer Energie als das tieferliegende AO und ein antibindendes MO mit höherliegender Energie als das höherliegende AO gebildet werden. Die Aufspaltung wird in erster Näherung vom Überlappintegral der zu kombinierenden Atomorbitale bestimmt. So kann man z. B. vorhersagen, dass eine σ-Bindung stärker aufspaltet als eine π-Bindung.

σ-Orbital

σ-Orbital
Molekülorbital von H₂
s-p-MO (z. B. Fluorwasserstoff)

Als σ-Orbital wird ein Orbital bezeichnet, das rotationssymmetrisch zur Bindungsachse ist. Es tritt demnach nur in Systemen mit 2 Atomen auf. Das σ-Orbital bildet sich als Kombination von Orbitalen mit der magnetischen Quantenzahl m_l = 0, d. h. s-, p- und d_z²-Orbitale.

Beispiele:

Das Wasserstoff-Molekülorbital entsteht durch Überlappung der 1s-Orbitale der Wasserstoffatome.
Im Fluorwasserstoff verbindet sich das kugelige 1s-Orbital des Wasserstoffatoms mit dem hantelförmigen 2p_x-Orbital des Fluoratoms zu einem Molekülorbital mit ungleichen Orbitalhälften. In der Realität hat auch das nicht eingezeichnete 2s-Orbital des Fluoratoms einen signifikanten Anteil am Bindungsorbital. (Die nichtbindenden 2p_y- und 2p_z-Orbitale sind ebenfalls nicht eingezeichnet.)

Beispiele in chemischen Verbindungen

Wasserstoff

Wasserstoff
bindend	antibindend
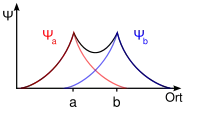Additive Überlagerung der Wellenfunktion, wobei a und b die Positionen der Protonen sind	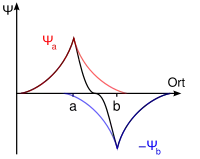Subtraktive Überlagerung der Wellenfunktion
Bindendes Molekülorbital	Antibindendes Molekülorbital
Besetzung der Molekülorbitale von Wasserstoff und Helium
Wasserstoff	Helium
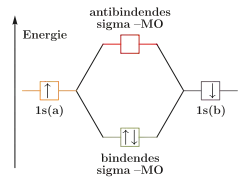Besetzung beim Wasserstoff	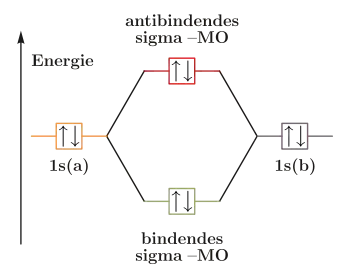Besetzung beim Helium

Die zur Bindung notwendigen vereinzelten Elektronen befinden sich jeweils im 1s-Orbital der beiden Atome H_a und H_b, das durch die Eigenfunktionen ψ_a(1s) und Ψ_b(1s) beschrieben wird.

Die Addition der Wellenfunktionen ψ_a(1s) + ψ_b(1s) ergibt ein rotationssymmetrisches bindendes Molekülorbital ( σ(1s) ) mit erhöhter Ladungsdichte zwischen den Kernen der Bindungspartner. Durch die Anziehung der Kerne durch die Ladung hält das Molekül zusammen.

Die Subtraktion der Wellenfunktionen ψ_a(1s) − ψ_b(1s) ergibt ein antibindendes Molekülorbital ( σ*(1s) ) mit einer Knotenebene zwischen den Kernen der Bindungspartner. Durch die resultierende geringe Elektronendichte zwischen den Kernen kommt es zu einer Abstoßung der Atome.

Die Molekülorbitale können (wie die Atomorbitale) mit maximal zwei Elektronen entgegengesetzten Spins besetzt werden. Da jedes Wasserstoffatom jeweils ein Elektron zur Verfügung stellt, wird das bindende Molekülorbital im energieärmsten Grundzustand mit einem Elektronenpaar besetzt, während das antibindende leer bleibt. (Im angeregten Zustand sind das bindende und das antibindende Molekülorbital mit je einem Elektron besetzt.)

Ein anderes Beispiel ist Helium. Hier ist jedes 1s-Orbital bereits mit einem Elektronenpaar besetzt. Bei der Kombination dieser Atomorbitale müsste sowohl das bindende als auch das antibindende Molekülorbital mit je einem Elektronenpaar besetzt werden. Ihre Wirkungen würden sich gegenseitig aufheben, es kommt keine Bindung zustande.

Sauerstoff

LCAO-MO-Schema von Triplett-Sauerstoff: Besetzung der Energieniveaus

Das LCAO-MO-Schema kann wie oben beschrieben qualitativ abgeleitet werden. Jedes Sauerstoff-Atom hat im Grundzustand sechs Valenzelektronen auf dem zweiten Hauptenergieniveau. Die zwölf Valenzelektronen eines O₂-Sauerstoffmoleküls werden auf die vier bindenden (σ_s, σ_x, π_y und π_z) und drei der vier antibindenden Molekülorbitale (σ_s^*, π_y^*, π_z^*) verteilt. Da zwei antibindende Orbitale mit nur einem Elektron besetzt sind (eine „halbe Bindung“), resultiert eine Doppelbindung.

Di-Sauerstoff hat im Grundzustand, einem Triplettzustand, gemäß der Hund’schen Regel zwei ungepaarte Elektronen parallelen Spins. Durch diese Elektronenverteilung lässt sich der Paramagnetismus und der diradikalische Charakter des Sauerstoffs erklären. Interessanterweise senkt der Diradikalcharakter die Reaktionsfähigkeit, da eine konzertierte Reaktion der Spinerhaltung widersprechen würde. Besonders reaktionsfähig ist der angeregte Singulett-Sauerstoff.

Eine weitere Folge der MO-Besetzung ist, dass es für O₂ schwierig ist, eine korrekte Lewis-Formel anzugeben. Entweder wird der Diradikalcharakter vernachlässigt oder die Doppelbindung.

1,3-Butadien

π-System des Butadiens

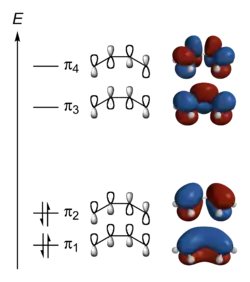
Das π-System des Butadiens setzt sich zusammen aus 4 p_z-Orbitalen, die am Anfang mit je einem Elektron besetzt sind. Diese 4 Atomorbitale werden nun zu vier Molekülorbitalen linear kombiniert. Die Koeffizienten erhält man durch variationelle Minimierung der Energie mit dem Rayleigh-Ritz-Prinzip z. B. mit der Hückel- oder der Hartree-Fock-Methode, oder durch symmetrieadaptierte Linearkombination (SALK). Dabei entstehen die rechts gezeichneten Orbitale. Die rot/blaue Färbung gibt an, ob das Orbital vor dem Quadrieren ein negatives oder positives Vorzeichen hatte. Physikalisch hat sie keine Relevanz.

Jedes dieser Orbitale kann mit 2 Elektronen besetzt werden. Es werden also die beiden unteren Orbitale voll aufgefüllt und die beiden oberen bleiben leer. Energetisch besonders günstig ist das Orbital, bei dem die Koeffizienten der p_z-Orbitale das gleiche Vorzeichen haben und sich daher die Elektronen fast frei über das ganze Molekül bewegen können.

Man erkennt die von SALK geforderte Eigenschaft, dass in jedem Molekülorbital alle Symmetrieelemente des Moleküls erhalten bleiben. Weiterhin sieht man, wie mit zunehmender Energie die Anzahl an Knotenebenen steigt.

Bindungsordnung

Die Bindungsordnung bezeichnet die Zahl der effektiven Bindungen zwischen zwei Atomen. Sie ist die Hälfte der Differenz der Zahl der bindenden und der antibindenden Valenzelektronen. Wenn keine Mesomerie auftritt, d. h. nur in einfachen Fällen, ist sie gleich der Anzahl der Bindungsstriche der Lewis-Schreibweise der Verbindung.

Geschichte

Die MO-Theorie geht auf die Arbeiten von Friedrich Hund, Robert S. Mulliken, John C. Slater und John Lennard-Jones zurück.[3] Die MO-Theorie wurde ursprünglich als Hund-Mulliken-Theorie bezeichnet.[4] Laut Erich Hückel wurde die erste quantitative Anwendung der MO-Theorie 1929 durch John Lennard-Jones entwickelt.[5][6] Die Veröffentlichung sagte einen Triplettzustand im Grundzustand des Sauerstoff-Moleküls voraus, wodurch sein Paramagnetismus erklärt wurde.[7] Zwei Jahre später wurde das Phänomen auch durch die VB-Theorie erklärt.[8] Im Jahr 1933 war die MO-Theorie bereits als valide anerkannt.[9]

Erich Hückel wandte 1931 die MO-Theorie zur Bestimmung der MO-Energien von π-Elektronen-Systemen auf ungesättigte Kohlenwasserstoffe an und beschrieb die Hückel-Molekülorbitale,[10][11] wodurch Aromatizität erklärt werden konnte. Die erste exakte Berechnung der MO-Wellenfunktion des Wasserstoffs erfolgte 1938 durch Charles Coulson.[12] Ab etwa 1950 wurden Molekülorbitale als Eigenfunktion behandelt (Hartree-Fock-Methode).[13] Die Hartree-Fock-Näherung wurde ursprünglich für einzelne Atome entwickelt und mit Basissätzen erweitert, was als Roothaan-Hall-Gleichungen beschrieben wurde.[14] In Folge wurden sowohl verschiedene Ab-initio-Berechnungen als auch semi-empirische Verfahren entwickelt.[14] In den 1930er Jahren wurde die Ligandenfeld-Theorie als Alternative zur Kristallfeld-Theorie entwickelt.

Siehe auch

Literatur

Thomas Engel: Physikalische Chemie. Pearson Deutschland GmbH, 2006, ISBN 978-3-8273-7200-0, S. 632.
Joachim Reinhold: Quantentheorie der Moleküle. Springer-Verlag, 2015, ISBN 978-3-658-09410-2, S. 127.

Weblinks

Commons: Molekülorbitale – Sammlung von Bildern, Videos und Audiodateien

MolecuLab, ein Flashprogramm mit Animationen zu Molekülorbitalen und ihrer Entstehung
Eintrag zu MO-Theorie. In: Römpp Online. Georg Thieme Verlag, abgerufen am 12. September 2017.

Einzelnachweise

Ian Fleming, Ian Fleming, Podlech, Joachim: Molekülorbitale und Reaktionen organischer Verbindungen. 1. Auflage. Wiley-VCH-Verl, Weinheim 2012, ISBN 978-3-527-33069-0, S. 1–11.
Frank Jensen: Introduction to Computational Chemistry. Wiley, 2007, ISBN 978-0-470-05804-6, S. 304–308.
Charles, A. Coulson: Valence. Oxford at the Clarendon Press, 1952.
Mulliken, Robert S.: Spectroscopy, Molecular Orbitals, and Chemical Bonding. (pdf) In: Elsevier Publishing Company (Hrsg.): Nobel Lectures, Chemistry 1963–1970. , Amsterdam1972.
Erich Hückel: Theory of free radicals of organic chemistry. In: Trans. Faraday Soc. 30, 1934, S. 40–52. doi:10.1039/TF9343000040.
J.E. Lennard-Jones: The electronic structure of some diatomic molecules. In: Trans. Faraday Soc. 25, 1929, S. 668–686. doi:10.1039/TF9292500668.
Coulson, C.A. Valence (2nd ed., Oxford University Press 1961), S. 103.
Linus Pauling: The Nature of the Chemical Bond. II. The One-Electron Bond and the Three-Electron Bond. In: J. Am. Chem. Soc.. 53, 1931, S. 3225–3237. doi:10.1021/ja01360a004.
George G Hall: Lennard-Jones Paper of 1929 Foundations of Molecular Orbital Theory. In: Advances in Quantum Chemistry. 22, Februar, ISSN 0065-3276. bibcode:1991AdQC...22....1H. doi:10.1016/S0065-3276(08)60361-5.
Erich Hückel: Quantentheoretische Beiträge zum Benzolproblem. I. Die Elektronenkonfiguration des Benzols und verwandter Verbindungen. In: Zeitschrift für Physik. Band 70, Nr. 3, 1. März 1931, S. 204–286, doi:10.1007/BF01339530.
Erich Hückel: Quanstentheoretische Beiträge zum Benzolproblem. II Quantentheorie der induzierten Polaritäten. In: Zeitschrift für Physik. Band 72, Nr. 5, 1. Mai 1931, S. 310–337, doi:10.1007/BF01341953.
Erich Hückel: Quantentheoretische Beiträge zum Problem der aromatischen und ungesättigten Verbindungen. III. In: Zeitschrift für Physik. Band 76, Nr. 9, 1. September 1932, S. 628–648, doi:10.1007/BF01341936.
Erich Hückel: Quantentheoretische Beiträge zum Problem der aromatischen und ungesättigten Verbindungen. IV Die freien Radikale der organischen Chemie. In: Zeitschrift für Physik. Band 83, Nr. 9, 1. September 1933, S. 632–668, doi:10.1007/BF01330865.
Hückel Theory for Organic Chemists, C. A. Coulson, B. O'Leary and R. B. Mallion, Academic Press, 1978.
C.A. Coulson: Self-consistent field for molecular hydrogen. In: Mathematical Proceedings of the Cambridge Philosophical Society. 34, Nr. 2, 1938, S. 204–212. bibcode:1938PCPS...34..204C. doi:10.1017/S0305004100020089.
G.G. Hall: The Molecular Orbital Theory of Chemical Valency. VI. Properties of Equivalent Orbitals. In: Proc. Roy. Soc. A. 202, Nr. 1070, 7. August 1950, S. 336–344. bibcode:1950RSPSA.202..336H. doi:10.1098/rspa.1950.0104.
Frank Jensen: Introduction to Computational Chemistry. John Wiley and Sons, 1999, ISBN 978-0-471-98425-2.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Ian Fleming, Ian Fleming, Podlech, Joachim: Molekülorbitale und Reaktionen organischer Verbindungen. 1. Auflage. Wiley-VCH-Verl, Weinheim 2012, ISBN 978-3-527-33069-0, S. 1–11.

[2] Frank Jensen: Introduction to Computational Chemistry. Wiley, 2007, ISBN 978-0-470-05804-6, S. 304–308.

[3] Charles, A. Coulson: Valence. Oxford at the Clarendon Press, 1952.

[Mulliken-4] Mulliken, Robert S.: Spectroscopy, Molecular Orbitals, and Chemical Bonding. (pdf) In: Elsevier Publishing Company (Hrsg.): Nobel Lectures, Chemistry 1963–1970. , Amsterdam1972.

[5] Erich Hückel: Theory of free radicals of organic chemistry. In: Trans. Faraday Soc. 30, 1934, S. 40–52. doi:10.1039/TF9343000040.

[6] J.E. Lennard-Jones: The electronic structure of some diatomic molecules. In: Trans. Faraday Soc. 25, 1929, S. 668–686. doi:10.1039/TF9292500668.

[7] Coulson, C.A. Valence (2nd ed., Oxford University Press 1961), S. 103.

[8] Linus Pauling: The Nature of the Chemical Bond. II. The One-Electron Bond and the Three-Electron Bond. In: J. Am. Chem. Soc.. 53, 1931, S. 3225–3237. doi:10.1021/ja01360a004.

[9] George G Hall: Lennard-Jones Paper of 1929 Foundations of Molecular Orbital Theory. In: Advances in Quantum Chemistry. 22, Februar, ISSN 0065-3276. bibcode:1991AdQC...22....1H. doi:10.1016/S0065-3276(08)60361-5.

[10] Erich Hückel: Quantentheoretische Beiträge zum Benzolproblem. I. Die Elektronenkonfiguration des Benzols und verwandter Verbindungen. In: Zeitschrift für Physik. Band 70, Nr. 3, 1. März 1931, S. 204–286, doi:10.1007/BF01339530.
Erich Hückel: Quanstentheoretische Beiträge zum Benzolproblem. II Quantentheorie der induzierten Polaritäten. In: Zeitschrift für Physik. Band 72, Nr. 5, 1. Mai 1931, S. 310–337, doi:10.1007/BF01341953.
Erich Hückel: Quantentheoretische Beiträge zum Problem der aromatischen und ungesättigten Verbindungen. III. In: Zeitschrift für Physik. Band 76, Nr. 9, 1. September 1932, S. 628–648, doi:10.1007/BF01341936.
Erich Hückel: Quantentheoretische Beiträge zum Problem der aromatischen und ungesättigten Verbindungen. IV Die freien Radikale der organischen Chemie. In: Zeitschrift für Physik. Band 83, Nr. 9, 1. September 1933, S. 632–668, doi:10.1007/BF01330865.

[11] Hückel Theory for Organic Chemists, C. A. Coulson, B. O'Leary and R. B. Mallion, Academic Press, 1978.

[12] C.A. Coulson: Self-consistent field for molecular hydrogen. In: Mathematical Proceedings of the Cambridge Philosophical Society. 34, Nr. 2, 1938, S. 204–212. bibcode:1938PCPS...34..204C. doi:10.1017/S0305004100020089.

[13] G.G. Hall: The Molecular Orbital Theory of Chemical Valency. VI. Properties of Equivalent Orbitals. In: Proc. Roy. Soc. A. 202, Nr. 1070, 7. August 1950, S. 336–344. bibcode:1950RSPSA.202..336H. doi:10.1098/rspa.1950.0104.

[Frank-14] Frank Jensen: Introduction to Computational Chemistry. John Wiley and Sons, 1999, ISBN 978-0-471-98425-2.