Hückel-Näherung
Die von Erich Hückel vorgeschlagene Hückel-Näherung, auch: Hückel-Molekülorbital-Modell/Methode (HMO-Modell/Methode), ist eine Methode der semiempirischen Quantenchemie. Ihre häufigste Anwendung ist es, Molekülorbitale in konjugierten π-Systemen zu approximieren. Hierbei liefert sie mit wenig Rechenaufwand erstaunlich gute Resultate. Die beiden wichtigsten Folgerungen sind die Hückel-Regel und die Woodward-Hoffmann-Regeln.
Anwendung
Die Näherung leitet sich vom Ritz'schen Verfahren unter Verwendung einer Basis von atomaren p-Orbitalen ab. Dabei wird formal das Eigenwertproblem reduziert auf . Im ersten Fall ist eine Eigenfunktion des Molekül-Hamiltonoperators . Um sie genau zu bestimmen, müsste bei einem n-atomigen Molekül eine 6n-dimensionale partielle Differentialgleichung gelöst werden, was analytisch i. Allg. nicht möglich ist. Im zweiten Fall ist der n-dimensionale Vektor, der die Koeffizienten zur Linearkombination enthält.
Nachdem berechnet wurde, kann das Molekülorbital als entsprechende Linearkombination der einzelnen pz-Orbitale angegeben werden. Der Wert E gibt die Energie des Orbitals wieder.
Im Ritz'schen Verfahren wird nach der Hartree-Fock-Methode iterativ eine möglichst gute Lösung gefunden. Dafür müssen in jedem Schritt eine große Zahl von Integralen gelöst werden, was hohen Rechenaufwand bedeutet. Die Vereinfachung der Hückelnäherung ist, dass alle Integrale parametrisiert werden.
Die n konjugierten Atome im Molekül werden durchnummeriert. Die Matrix ist eine n×n-Matrix. Man setzt:
hii = αi
hij = β, falls die beiden Atome benachbart sind (und über Konjugation verknüpft), und
hij = 0 sonst.
αi ist dabei das Coulombintegral des Atoms i im Molekül (αi<0)
(* ist dabei die komplexe Konjugation, V bezeichnet das ganze Volumen)
β das Resonanzintegral zwischen zwei Atomen i,j (wird für alle Atompaare als gleich angenommen) (β<0)
Der Sinn der Näherung ist, dass diese beiden Integrale nicht berechnet werden. Sie können zum Beispiel anhand von empirischen Daten geschätzt werden. Für zwei Atome von derselben Art werden die Coulombintegrale gleichgesetzt. Besonders einfach kann man daher reine Kohlenwasserstoffe berechnen. Es bleiben nur zwei Konstante α und β übrig. Die Eigenvektoren sind unabhängig von deren Wert.
Ableitung der Hückel-Regel
Der Frost-Kreis bietet eine einfache Möglichkeit, die Stabilität zyklisch-konjugierter ebener Moleküle abzuschätzen. Sie basiert auf der überraschenden Tatsache, dass das Energieniveauschema eines zyklisch-konjugierten ebenen n-atomaren Moleküls als regelmäßiges n-Eck dargestellt werden kann (unter der Voraussetzung, dass das ebene Molekül eine n-zählige Hauptdrehachse aufweist).
Die zu einem n-Ring gehörige n×n-Matrix wird gebildet, indem man in die Hauptdiagonale α schreibt, in die beiden Nebendiagonalen β und in die linke untere sowie die rechte obere Ecke ebenfalls β:
Die Eigenwerte dieser Matrix ergeben sich zu . Trägt man nun die Energie entlang der y-Achse auf, beachtet, dass β negativ ist und hält entsprechende Abstände in x-Richtung ein, so erhält man ein auf der Spitze stehendes n-Eck.
- Beispiele für aromatische Verbindungen
_with_MO_diagram.png.webp)
_with_MO_diagram.png.webp)
_with_MO_diagram.png.webp)
Dieses n-Eck kann nun mit einer ungeraden Zahl von Elektronenpaaren (4n+2 π-Elektronen) unter hohem Energiegewinn besetzt werden. Diese Moleküle werden als „Aromaten“ bezeichnet. Bei einer geraden Zahl von Elektronenpaaren (4n π-Elektronen) wären die beiden obersten Niveaus gemäß der Hundschen Regel halbbesetzt, das Molekül paramagnetisch und der gesamte Energiegewinn gering. Diese Verbindungen sind instabil und heißen „Antiaromaten“.
- Beispiele für antiaromatische Verbindungen
_with_MO_diagram.png.webp)
_with_MO_diagram.png.webp)
Beispiel
Benzol
Die Hückelmatrix lautet:
Die Eigenwerte ergeben sich zu:
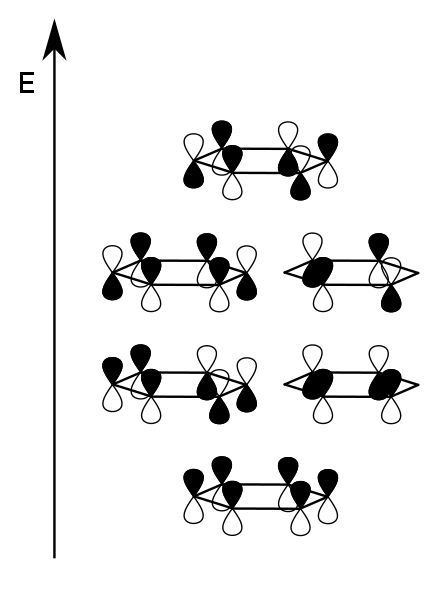
Die Eigenvektoren zu den jeweiligen Eigenwerten:
((1, 1, 1, 1, 1, 1), (1, 0, -1, -1, 0, 1), (-1, -1, 0, 1, 1, 0), (-1, 1, 0, -1, 1, 0), (-1, 0, 1, -1, 0, 1), (-1, 1, -1, 1, -1, 1))
Ein Schnitt (parallel zur xy-Ebene in 75 pm Entfernung) durch die entsprechenden Orbitale ist rechts gezeichnet. Die Koordinaten der Vektoren bedeuten jeweils das Vorzeichen der pz-Wellenfunktionen. Diese sind angefangen von rechts gegen den Uhrzeigersinn durchgezählt.
Gemäß einem auf der Spitze stehenden 6-Eck gibt es 3 stabilisierte und drei destabilisierte Orbitale. 6 Elektronen können also unter hohem Energiegewinn die unteren drei Orbitale besetzen. Die Gesamtbindungsenergie ist 2·2 β + 4 β = 8 β. Dieser Wert ist deutlich höher als 6 β für drei isolierte π-Bindungen.
Quellen
- Peter W. Atkins: Physikalische Chemie. Weinheim [u. a.] : VCH-Verl.-Ges.
- Dietmar Dorninger: Mathematische Grundlagen für Chemiker. Eisenstadt : Prugg
Literatur
G. Frenking: Perspective on „Quantentheoretische Beiträge zum Benzolproblem. I. Die Elektronenkonfiguration des Benzols und verwandter Beziehungen“. In: Theoretical Chemistry Accounts. Band 103, 2000, S. 187–189, doi:10.1007/s002149900023.