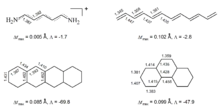Aromatizität

Aromatizität[1][2] ist ein Konzept aus dem Bereich der chemischen Bindung, das eingeführt wurde, um die auffallenden Eigenschaften der Stoffklasse der Aromaten zu erklären. Es beschreibt das Phänomen, dass cyclische Delokalisation von 4n + 2 π-Elektronen (Hückel-Regel) in einem planaren Molekül zu einer energetischen Stabilisierung führt, die mit dem Auftreten von diamagnetischen Ringstromeffekten, Anisotropie der magnetischen Suszeptibilität, magnetic susceptibility exaltation[3] sowie einer Tendenz zum Bindungslängenausgleich einhergeht. Das Phänomen der Aromatizität ist keine summarische Observable, hingegen sind die einzelnen Kriterien messbar. Jedoch sind für die einzelnen Kriterien keine festen oder klaren Grenzwerte zur Abgrenzung aromatisch – nichtaromatisch - antiaromatisch festgelegt. Üblicherweise erfolgt die Diskussion über das Ausmaß der Aromatizität einzelner Verbindungen unter Bezug auf eine Referenz. Hierbei gilt Benzol unumstritten als Paradebeispiel für ein aromatisches System.

Während sich ursprünglich die Diskussion der Aromatizität auf cyclisch konjugierte π-Systeme beschränkt hat, ist der Aromatizitätsbegriff heute deutlich weiter gefasst und um Homoaromatizität, σ-Aromatizität,[4][5] σ-Homoaromatizität, räumliche Aromatizität,[6] Superaromatizität etc. ergänzt. Insbesondere die Entwicklung quantenchemischer Methoden hat dabei die Erweiterung des theoretischen Verständnisses signifikant unterstützt.

Sind in einem Molekül statt 4n + 2 Elektronen 4n Elektronen cyclisch delokalisiert, so beobachtet man das Phänomen der Antiaromatizität. In diesem Fall erfolgt eine Destabilisierung des Systems. Antiaromatische Systeme werden somit versuchen, der ungünstigen Situation zu entgehen und durch geometrische Veränderung (Verzerrung, Jahn-Teller-Effekt) die cyclische Delokalisation zu verringern. Ein Paradebeispiel hierfür ist Cyclobutadien.

Eine Übersicht der Charakteristika von aromatischen und antiaromatischen Systemen im Vergleich zu linear-konjugierten Referenzen fasst die nachfolgende Tabelle zusammen:[7]

Eigenschaft	Aromat	Referenz (Olefin)	Antiaromat
Delokalisation / Konjugation	cyclisch	linear	cyclisch
Zahl der π-Elektronen	4n + 2	2n	4n
Energetischer Effekt der Konjugation	Stabilisierung	= Referenz	Destabilisierung
Ausmaß der Delokalisation	erhöht	= Referenz	erniedrigt
Bindungslängen	Tendenz zum Bindungslängenausgleich	alternierend	alternierend
Diamagnetische Anisotropie	erhöht	-	klein
magnetic susceptibility exaltation[3]	hoch	-	niedrig
Ringstrom	diamagnetisch	-	paramagnetisch
NICS-Werte	deutlich negativ	-	deutlich positiv
Chemische Reaktivität	elektrophile Substitution	Addition	Addition
HOMO-LUMO-Differenz	erhöht	= Referenz	erniedrigt
Typische Vertreter	Benzol	Butadien	Cyclobutadien

Entwicklung des Aromatizitätsbegriffs

Aromatizität wurde zunächst im Sinne olfaktorischer und chemischer Eigenschaften beschrieben: besonders „aromatisch“ riechende Verbindungen zeigten für ungesättigte Verbindungen verblüffend geringe Reaktivität. So wird z. B. Brom nicht spontan an die Doppelbindungen von Benzol addiert. Benzol und seine Derivate reagieren zudem bevorzugt nach dem Muster der elektrophilen aromatischen Substitution (Additions-Eliminierungsmechanismus, der zur Aufrechterhaltung der cyclischen Delokalisation führt) und nicht unter einfacher Addition an eine der (formalen) Doppelbindungen. Während sich frühe Arbeiten auf synthetische Methoden stützten – z. B. Versuche, über die Zahl an Isomeren die cyclische Struktur von Benzol nachzuweisen und die Frage zu klären, ob Alternanz von Doppel- und Einfachbindungen vorliegt – wurden im Zuge der Entwicklung der (Elektronen-)Theorie der chemischen Bindung mehr und mehr physikalische Aspekte in die Untersuchungen einbezogen. Eine erschöpfende Zusammenstellung wichtiger Meilensteine der Entwicklung des Aromatizitätsbegriffs und der Kriterien zur Definition von Aromatizität findet sich bei Schleyer et al.[8] – einige Kernaspekte können der nachfolgenden Tabelle entnommen werden:[1]

Jahr	Aspekt
1865	Kekulé: Benzolstruktur[9]
1866	Erlenmeyer: Vorherrschen von elektrophiler Substitution statt Addition[10]
1910	Pascal: Aromaten haben erhöhte diamagnetische Suszeptibilität[11]
1925	Armit & Robinson: Elektronensextett und Heteroaromatizität[12]
1931	Hückel: Stabilisierung der 4n + 2-, Destabilisierung der 4n-Elektronensysteme (Hückel-Regel)[13]
1936 / 1937	London, Pauling: Theorie der Ringstromeffekte[14][15]
1956	Pople: Einfluss von Ringstromeffekten auf NMR-Verschiebungen[16]
1969 / 1970	Dauben / Benson & Flygare: magnetische Suszeptibilität (Erhöhung und Anisotropie) als Aromatizitätskriterien[3][17]
1979	Aihara: Dreidimensionale Aromatizität[18]
1980	Kutzelnigg: Quantenchemische Berechnung (IGLO) von NMR- und magnetischen Moleküleigenschaften[19]
1984	Dewar: σ-Aromatizität von Cyclopropan[4]
1996	Schleyer: Einführung von NICS als einfache quantenchemische Methode zur Untersuchung der Aromatizität[20]

Für eine Übersicht der frühen Geschichte der Untersuchung der Aromaten vgl. z. B. unter Benzol.

Arten der Aromatizität

π-Aromatizität

Beim archetypischen Fall von Aromatizität findet cyclische Delokalisation durch Konjugation von π-Orbitalen entlang eines geschlossenen Perimeters statt, der von σ-Bindungen definiert wird.

Hetero-Aromatizität

Ausgehend von benzoiden Aromaten werden einzelne Kohlenstoff-Atome durch Heteroatome ersetzt. Pyridin, Thiophen, Furan, Pyrrol sind typische Beispiele.

σ-Aromatizität

Bei kleinen Ringen (insbesondere bei Cyclopropanen) wird cyclische Delokalisation in der σ-Ebene beobachtet. Wie bei der π-Aromatizität werden energetische Stabilisierung und die für diamagnetische Ringströme typischen magnetischen Eigenschaften beobachtet. Bei rein anorganischen Systemen gilt das cyclische Ion H₃⁺ als Paradebeispiel für σ-Aromatizität. Auch für trigonale Metallcluster von Zn und Au wird σ-Aromatizität diskutiert.[21]

Homoaromatizität[22]

Wird im Falle der π-Aromaten der geschlossene Perimeter aus σ-Bindungen an einer Stelle unterbrochen, z. B. durch Einführung einer Methylen-Gruppe, so kann an dieser Position bei ausreichenden geometrischen Bedingungen die π-Konjugation durch den Raum (through space) aufrechterhalten werden. Paradebeispiel für dieses Phänomen ist das Homotropylium-Kation. Ist der Perimeter an mehreren Stellen unterbrochen, spricht man von Bishomo-, Trishomo-Aromatizität usw.

σ-Homoaromatizität

Wie bei den π-Aromaten kann bei kleinen Ringen die σ-Konjugation durch den Raum erfolgen (through space). Beispiele für σ-Bishomoaromatizität in 2- und 6-Elektronensystemen sind beschrieben.

Sphärische Aromatizität (Räumliche Aromatizität, 3D-Aromatizität)[23]

Aromatizität in drei Dimensionen ist beschrieben für Cluster-Verbindungen wie Borane und Fullerene.

Aromatische Stabilisierungsenergie

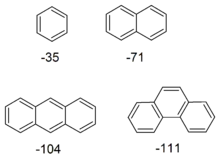
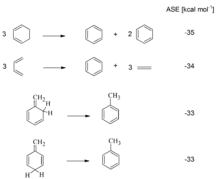
ASE [kcal mol⁻¹] aus thermochemischen Messungen[24]

ASE von Benzol abgeschätzt aus homodesmotischen Reaktionsschemata und ISE-Rechnungen nach Schleyer et al.[8]

Eine früh bekannte Auffälligkeit von Benzol war die Tatsache, dass sich Benzol – im Gegensatz zu anderen ungesättigten Verbindungen – nur vergleichsweise schwer hydrieren lässt. Bei thermochemischen Messungen fiel zudem auf, dass die im Falle von Benzol freiwerdende Hydrierwärme gegenüber einem hypothetischen nichtaromatischen Cyclohexatrien signifikant reduziert ist. Aus dieser Differenz wurde eine aromatische Stabilisierungsenergie des Benzols (ASE) von −150 kJ/mol (−36 kcal/mol) abgeleitet.[25] (Die Vorzeichenkonvention der ASE wird in der Literatur leider nicht immer stringent eingehalten. In diesem Artikel wird für aromatische Verbindungen eine negative ASE (Stabilisierung!) und eine positive ASE (Destabilisierung!) für antiaromatische Verbindungen verwendet.)

Neben thermochemischen Messungen stehen heute eine Vielzahl von quantenchemischen Methoden zur Verfügung, um aromatische Stabilisierungsenergien abzuschätzen.[26] Üblicherweise geschieht dies anhand von homodesmotischen Reaktionen.[27][28] Durch Verwendung von homodesmotischen Reaktionsgleichungen sollen sich dabei Ungenauigkeiten, die sich aus der Qualität der verwendeten Rechenmethoden ergeben, herausmitteln, so dass die interessierende Größe in hoher Genauigkeit erhalten wird. Unabhängig davon, ob die Abschätzung der aromatischen Stabilisierungsenergie nun über thermochemische Messungen oder Berechnungen erfolgt, muss stets beachtet werden, dass die aromatische Stabilisierungsenergie keine Observable ist. Die ASE hängt damit von den gewählten Referenzverbindungen ab und ist zudem nicht leicht von anderen Effekten – etwa Ringspannungen – zu trennen. Auch müssen Stabilisierungseffekte durch Resonanz herausgerechnet werden, die nicht auf der cyclischen Delokalisation beruhen und somit zwar zur gesamten Resonanzenergie aber nicht zur ASE beitragen. Diese Probleme zeigen sich bereits deutlich bei der Berechnung der ASE von Benzol: selbst bei sorgfältiger Auswahl der Referenzstrukturen für homodesmotische Reaktionen schwanken die berechneten Werte leicht um 10 kcal mol⁻¹, wie eine Zusammenstellung von Cyrański zeigt.[26] Um das Problem zu umgehen, schlugen Schleyer et al. vor, Isomerisierungsreaktionen anstelle von homodesmotischen Reaktionsschemata zur Ermittlung der ASE heranzuziehen.[29] Die berechneten isomerization stabilization energies (ISE) sind dabei in guter Übereinstimmung mit Vergleichswerten aus sorgfältig ausgewählten homodesmotischen Reaktionsschemata.

Eine Reihe von Schleyer et al. anhand einer "homodesmotischen"[30] Reaktion berechneten ASEs für 5-gliedrige Ringverbindungen belegen sowohl die Hückel-Regel als auch das schon früh bekannte Phänomen der Heteroaromatizität:[31]

	ASE [kcal mol⁻¹]
X	CH	CH₂	SiH	BH	NH	O	S
Name von C₄H₄X		Cyclopentadien		Borol	Pyrrol	Furan	Thiophen
Kation	57		24
Neutralverbindung		−4[32]		19	−26	−20	−22
Anion	−29		−14

Aromatizität und Antiaromatizität in Cyclopropenyl- und Cyclopentadienyl-Ionen. Enthalpien berechnet auf G2-Niveau.[33]

Das Kriterium der aromatischen Stabilisierungsenergie folgt der "praktischen Erfahrung" der Chemiker, dass sich aromatische Verbindungen durch besondere Stabilität auszeichnen (negativer Wert für die ASE). Die oben angeführten Werte für antiaromatische Systeme (Tabelle, 5-Ring-Systeme mit 4n π-Elektronen) sind hiermit in Einklang (Destabilisierung durch Antiaromatizität). Cyclobutadien, ein Paradefall für Antiaromatizität, erfährt nach der Abschätzung

Cyclobutadien + Cyclobutan → 2 Cyclobuten

eine Destabilisierung von +36 kcal/mol.[1]

Eindrückliche Beispiele dafür, dass cyclische Konjugation von 4n + 2 Elektronen zu einer Stabilisierung, cyclische Konjugation von 4n Elektronen dagegen zu einer Destabilisierung führt, liefern isodesmische Reaktionen von Cyclopropen bzw. Cyclopentadien mit Cyclopropyl- bzw. Cyclopentyl-Anionen und -Kationen (vgl. nebenstehende Abbildung). Die Bildung von aromatischen Ionen wird dabei durch hohe Exothermie, die Bildung von antiaromatischen Ionen durch deutliche Endothermie angezeigt.

NMR-Effekte, NICS

Protonenresonanzen (NMR) von Benzol, Cyclohexan, Vogel-Aromat (Methano[10]annulen) und [18]Annulen nach Schleyer et al.[8]

In NMR-Experimenten lässt sich der Effekt der cyclischen Elektronendelokalisation in aromatischen Verbindungen durch die damit einhergehenden magnetischen Effekte (Ringstromeffekt) nachweisen: das durch den Ringstrom induzierte magnetische Feld führt bei Benzol zu einer Protonenresonanz bei 7,3 ppm (Entschirmung), wohingegen vergleichbare vinylische Protonen in Cyclohexen bei 5,6 ppm erscheinen. Protonen, welche sich oberhalb oder im inneren Bereich eines aromatischen π-Systems befinden, erfahren dagegen eine Abschirmung. Lehrbuchbeispiele für diesen Effekt sind z. B. die Methylenprotonen im Methano[10]annulen (Vogel-Aromat) oder die inneren Protonen im [18]Annulen.[8]

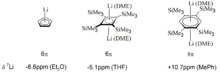
Li-NMR-Verschiebungen von aromatischen und antiaromatischen Verbindungen[8]

Neben den Protonenresonanzen wurden auch die chemischen Verschiebungen von Li⁺ häufig zum Studium der aromatischen Eigenschaften anionischer π-Systeme herangezogen, da Lithium in der Regel in zentraler Position oberhalb des π-Systems elektrostatisch bindet und somit eine wenig störanfällige Probe für die magnetischen Eigenschaften der zu untersuchenden Spezies darstellt. Typische Beispiele für diese Herangehensweise finden sich in den Li-Salzen der (Di)Anionen von Cyclopentadien, Tetrakis-trimethylsilyl-cyclobutadien und dem antiaromatischen Dianion von Tetrakis-trimethylsilyl-benzol (vgl. Abbildung).[8]

NICS(0)-Werte berechnet auf B3LYP/6-311+G**-Niveau nach Schleyer et al.[8]

Mit der Einführung quantenchemischer Methoden wurde es möglich, chemische Verschiebungen (Abschirmungen) an einer beliebigen Stelle im Raum zu berechnen und somit Ringstromeffekte unabhängig von einzelnen Atomkernen zu evaluieren. Die Methode wurde von ihren Protagonisten Nucleus Independent Chemical Shifts (NICS) benannt.[8] Zum Studium aromatischer Verbindungen werden NICS-Werte in der Regel im geometrischen Mittelpunkt der Schweratome (d. h. der nicht-Wasserstoffatome, nicht massengemittelt) berechnet. Wie im Falle von Protonen gewohnt, zeigen negative NICS-Werte im inneren von cyclisch delokalisierten Systemen eine diamagnetischen Ringstrom und somit Aromatizität an. Positive NICS-Werte indizieren dagegen Antiaromatizität.

Obwohl die cyclische Elektronendelokalisation die magnetischen Eigenschaften (anti)aromatischer Moleküle dominiert, zeigen auch lokalisierte Bindungen und lone pairs zumindest kurzreichweitige magnetische Effekte, welche die berechneten NICS-Werte beeinflussen können. Um diesen Störfaktor auszuschalten, können bei planaren Molekülen NICS-Werte oberhalb der π-Ebene berechnet werden. Aufwändigere Methoden erlauben es ferner, NICS-Beiträge von σ- und π-Bindungen oder auch von einzelnen Molekülorbitalen zu berechnen und somit zu separieren.

Magnetische Suszeptibilität

Die magnetische Suszeptibilität χ ist eine aus der Physik bekannte Größe und beschreibt, wie stark sich ein Stoff beim Einbringen in ein Magnetfeld magnetisieren lässt. Die magnetische Suszeptibilität lässt sich auf Beiträge entlang der drei Raumrichtungen (x, y, z) zurückführen und wird in der Chemie meist als molare Größe verwendet. Für ungeordnete Flüssigkeiten ergibt sich dabei die beobachtbare Suszeptibilität als Mittelwert aus den drei Suszeptibilitäten der Moleküle entlang der Raumrichtungen:

χ_M = 1/3 (χ_x + χ_z + χ_z)

Orientiert man benzoide Aromaten derart, dass das Molekül in der xy-Ebene zu liegen kommt, so ist die magnetische Suszeptibilität in z-Richtung deutlich größer als innerhalb der Molekülebene. Dieses Phänomen wird als erhöhte diamagnetische Anisotropie bezeichnet und durch folgende Gleichung beschrieben:

Δχ = χ_z − 1/2 (χ_x + χ_y) >> 0

Da die experimentelle Bestimmung der anisotropen Eigenschaften schwierig ist[34] und nur an Einkristallen vorgenommen werden kann, wurden einfachere Kriterien zur Beschreibung der magnetischen Eigenschaften von organischen Molekülen zu Studium der Aromatizität gesucht. Einen eleganten Ansatz schlugen Dauben, Wilson und Laity vor:[3] ähnlich wie sich thermodynamische Größen für Moleküle aus entsprechenden Inkrementen für die enthaltenen Bindungen abschätzen lassen, können magnetische Suszeptibilitäten auf Bindungs-spezifische Beiträge zurückgeführt werden. Im Falle von aromatischen Verbindungen stellt man dabei fest, dass die gemessenen Suszeptibilitäten gegenüber den aus Inkrementen abgeschätzten Werten erhöht sind. Dieser Effekt wird auf die besonderen magnetischen Effekte durch die cyclische Delokalisation zurückgeführt. Für den Effekt wurde die Bezeichnung magnetic susceptibility exaltation eingeführt gemäß der Gleichung

Λ-Werte für Kohlenwasserstoffe in −10⁻⁶ cm³ mol⁻¹ nach Dauben et al.[3]

Λ = χ_M (gemessen) − χ_M (Inkrement)

Für aromatische Moleküle gilt Λ >> 0, nicht-aromatische Moleküle zeigen Λ ~ 0. Da antiaromatische Moleküle versuchen, die cyclische Delokalisation durch geometrische Veränderung zu minimieren, werden keine signifikant negativen Λ-Werte ermittelt (vgl. Cyclooctatetraen).

Anhand der in der nebenstehenden Abbildung aufgeführten Werte für "klassische" Aromaten lässt sich ableiten, dass diese sich durch Λ > 12 auszeichnen und die Größe von Λ mit der Größe der π-Systeme korreliert. Die Reihe Cyclooctan → Cyclooctatetraen belegt, dass die einfache Einführung von Doppelbindungen sowie deren nicht-cyclische Konjugation nur vernachlässigbaren Einfluss auf die Größe von Λ haben. Cyclooctatetraen schließlich weicht dem energetisch ungünstigen antiaromatischen Zustand durch geometrische Verzerrung weitgehend aus, so dass zwar ein negativer Wert für Λ ermittelt wird, dieser fällt jedoch mit −0,9 überraschend gering aus. Interessante Sonderfälle werden bei Cyclopentadien und 5,5-Dimethylcyclopentadien sowie bei Cycloheptatrien angetroffen. Die auffallend hohen Werte der magnetischen Suszeptibilitätserhöhung wurden bei den Cyclopentadienen als Hinweis auf aromatischen Charakter durch Einbeziehung von zwei Elektronen aus den CH/CC-Bindungen der Methyleneinheit interpretiert, der hohe Λ-Wert von Cycloheptatrien ist in Einklang mit dem Effekt der Homoaromatizität.

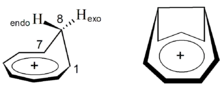
Homotropylium-Kation und das von Cremer et al. untersuchte Bishomotropylium-Kation[35]

Eine zeitweilige Renaissance hat die Betrachtung magnetischer Suszeptibilitäten durch Einführung leistungsfähiger quantenmechanischer Methoden erfahren. So nutzten Cremer et al. berechnete magnetische Suszeptibilitäten zum Nachweis der homoaromatischen Natur des Homotropylium-Kations.[36] Bei Variation der C1-C7-Bindungslänge zeigt das Kation in seiner Gleichgewichtsgeometrie die höchste magnetische Suszeptibilität. Der Effekt geht einher mit der größten Differenz der chemischen Verschiebungen von H8-endo und H8-exo, der größten Angleichung der C1–C7 ¹³C-Resonanzen sowie dem stärksten Bindungslängenausgleich zwischen den an der cyclischen Delokalisation beteiligten Kohlenstoff-Atomen. Diese Untersuchungen wurden unter anderem auf ein bishomoaromatisches 1,4-Bishomotropylium-Kation ausgedehnt.[35]

Herges und Schleyer nutzten quantenchemisch berechnete magnetische Suszeptibilitäten und deren Anisotropien, um den aromatischen Charakter von Übergangszuständen von pericyclischen Reaktionen wie z. B. der Diels-Alder-Reaktion nachzuweisen.[37] Die Berechnung von magnetischen Suszeptibilitäten und ihren Anisotropien ist heute jedoch von anderen Methoden wie der Berechnung von NICS-Werten oder auch der Visualisierung und Quantifizierung von induzierten Ringströmen abgelöst worden, die einen detaillierteren Einblick in das Phänomen der Aromatizität geben.

Geometrische Effekte

CC-Bindungslängen und Λ-Werte für Tetracen und Phenanthren verglichen mit linear-konjugierten Systemen nach Schleyer et al.[1][8]

Als charakteristisches Merkmal der cyclischen Elektronendelokalisation wird immer wieder – ausgehend vom "klassischen" Fall der π-Aromatizität – der Bindungslängenausgleich zwischen Einfach- und Doppelbindungen herausgestellt. Benzol, als Archetypus der Aromaten, zeigt dieses Phänomen in Perfektion, ebenso wie Borazin, das allenfalls als Grenzfall für Aromatizität gelten kann (starke Lokalisation der Elektronen an den Stickstoffatomen, geringer Ringstrom). Schleyer et al. weisen darauf hin, dass die Bindungslängendifferenzen in polycyclischen Aromaten sich nicht signifikant von denen linear konjugierter Polyene unterscheiden müssen und unter Umständen sogar in den linearen Systemen kleiner ausfallen können (vgl. Abbildung). Bindungslängenausgleich ist somit für sich allein genommen kein hinreichendes Kriterium für aromatischen Charakter.[1][8]

Einzelnachweise

P. von Ragué-Schleyer, Haijun Jiao: What is aromaticity?. In: Pure and Applied Chemistry. 68, 1996, S. 209, doi:10.1351/pac199668020209.
Eintrag zu aromaticity. In: IUPAC (Hrsg.): Compendium of Chemical Terminology. The “Gold Book”. doi:10.1351/goldbook.A00442 – Version: 2.3.3.
Hyp J. Dauben, James Dennis. Wilson, John L. Laity: Diamagnetic susceptibility exaltation as a criterion of aromaticity. In: Journal of the American Chemical Society. 90, 1968, S. 811, doi:10.1021/ja01005a059.
Michael J. S. Dewar: Chemical implications of σ conjugation. In: Journal of the American Chemical Society. 106, 1984, S. 669, doi:10.1021/ja00315a036.
Dieter Cremer: Pros and cons of σ-aromaticity. In: Tetrahedron. 44, 1988, S. 7427, doi:10.1016/S0040-4020(01)86238-4.
Z. Chen, R. B. King: Spherical Aromaticity: Recent Work on Fullerenes, Polyhedral Boranes, and Related Structures. In: Chem. Rev., 2005, 105, S. 3613–3642.
Eine Übersicht der aktuellen Diskussion zum Thema Aromatizität und Antiaromatizität findet sich in Chemical Reviews Vol. 101, Heft 5, 2001 sowie Vol. 105, Heft 10, 2005.
Z. Chen, C.S. Wannere, C. Corminboeuf, R. Puchta, P. v. R. Schleyer: Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion. In: Chemical Reviews, 2005, 105, S. 3842, doi:10.1021/cr030088+
A. Kekulé: Sur la constitution des substances aromatique. In: Bull. Soc. Chim. Paris, 1865, 3, S. 98–111. pdf
E. Erlenmeyer: Studien über die s. g. aromatischen Säuren. In: Ann., 1866, 137, S. 327–359.
P. Pascal: Recherches Magnétochimiques. In: Ann. Chim. Phys., 1910, 19 (8), S. 5–70. pdf
J. W. Armit, R. Robinson: CCXI.—Polynuclear heterocyclic aromatic types. Part II. Some anhydronium bases. In: J. Chem. Soc., Trans., 1925, 127, S. 1604–1618.
E. Hückel: Quantentheoretische Beiträge zum Benzolproblem. In: Z. Physik, 1931, 70, 204–286 und 72, S. 310–337.
L. Pauling: The Diamagnetic Anisotropy of Aromatic Molecules. In: J. Chem. Phys., 1936, 4, S. 673–677.
F. London: Théorie quantique des courants interatomiques dans les combinaisons aromatiques. In: J. Phys. Radium 1937, 8, S. 397–409.
J. A. Pople: Proton Magnetic Resonance of Hydrocarbons. In: J. Chem. Phys., 1956, 24, S. 1111.
R. C. Benson, W. H. Flygare: Molecular Zeeman effect of cyclopentadiene and isoprene and comparison of the magnetic susceptibility anisotropies. In: J. Am. Chem. Soc., 1970, 92, S. 7523–7529.
J. Aihara: Three-dimensional aromaticity of polyhedral boranes. In: J. Am. Chem. Soc., 1978, 100, S. 3339–3342.
W. Kutzelnigg: Theory of Magnetic Susceptibilities and NMR Chemical Shifts in Terms of Localized Quantities. In: Isr. J. Chem., 1980, 19, S. 193–200.
P. v. Ragué-Schleyer, C. Maerker, A. Dransfeld, H. Jiao, N. J. R. v. E. Hommes: Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. In: J. Am. Chem. Soc., 1996, 118, S. 6317–6318.
K. Freitag, C. Gemel, P. Jarabek, I. M. Oppel, R. W. Seidel, G. Frenking, H. Banh, K. Dilchert, R. A. Fischer: The σ-Aromatic Clusters [Zn₃]⁺ and [Zn₂Cu]: Embryonic Brass. In: Angew. Chem. Int. Ed., 2015, 54, S. 4370–4374.
R. V. Williams: Homoaromaticity. In: Chem. Rev., 2001, 101, S. 1185–1204.
Z. Chen, R. B. King: Spherical Aromaticity: Recent Work on Fullerenes, Polyhedral Boranes, and Related Structures. In: Chem. Rev., 2005, 105, S. 3613–3642.
J. D. Roberts, M. C. Caserio: Basic Principles of Organic Chemistry, W. A. Benjamin Inc., New York, Amsterdam, 1965.
Alan R. Katritzky, Karl Jug, Daniela C. Oniciu: Quantitative Measures of Aromaticity for Mono-, Bi-, and Tricyclic Penta- and Hexaatomic Heteroaromatic Ring Systems and Their Interrelationships. In: Chem. Rev., 2001 101, S. 1421–1449, doi:10.1021/cr990327m und dort zitierte Literatur.
Michał Ksawery Cyrański: Energetic Aspects of Cyclic Pi-Electron Delocalization: Evaluation of the Methods of Estimating Aromatic Stabilization Energies. In: Chem. Rev. 2005, 105, S. 3773–3811, doi:10.1021/cr0300845.
Eintrag zu homodesmotic reaction. In: IUPAC (Hrsg.): Compendium of Chemical Terminology. The “Gold Book”. doi:10.1351/goldbook.HT07048 – Version: 2.3.3.
Der Begriff "homodesmotisch" wird in der Literatur nicht immer einheitlich verwendet. Ein kritischer Kommentar und ein Vorschlag zur Vereinheitlichung findet sich in S. E. Wheeler, K. N. Houk, P. v. R. Schleyer, W. D. Allen: A Hierarchy of Homodesmotic Reactions for Thermochemistry. In: J. Am. Chem. Soc., 2009, 131, S. 2547–2560.
Schleyer et al. in Chem. Rev., 2005, 105, S. 3842–3888 und dort zitierte Literatur.
Die verwendete Reaktion wird von den Autoren zwar als homodesmotisch bezeichnet, erfüllt die Begriffsdefinition jedoch nicht, vgl. die Diskussion durch Cyrański in Chem. Rev., 2005, 105, S. 3773–3811.
P. v. Ragué-Schleyer, P. Freeman, H. Jiao, B. Goldfuss: Aromaticity and Antiaromaticity in Five-Membered C₄H₄X Ring Systems: “Classical” and “Magnetic” Concepts May Not Be “Orthogonal”. In: Angew. Chem. Int. Ed., 1995, 34, S. 337–340.
Cyclopentadien wird von den Autoren als Grenzfall eines aromatischen Systems diskutiert, wobei die cyclische Delokalisation durch Einbeziehen von zwei Elektronen der CH2-Gruppe erreicht wird. Vgl. hierzu auch die im Artikel zitierte Literatur.
Kenneth B. Wiberg: Antiaromaticity in Monocyclic Conjugated Carbon Rings. In: Chemical Reviews. 101, 2001, S. 1317, doi:10.1021/cr990367q.
Moderne quantenchemische Rechenmethoden erlauben es heute, die magnetischen Eigenschaften von Molekülen zu berechnen. Derartige Methoden standen nicht zur Verfügung als das Kriterium der diamagnetischen Anisotropie zum Studium aromatischer Verbindungen eingeführt wurde.
D. Cremer, P. Svensson, E. Kraka, Z. Konkoli, P. Ahlberg: Exploration of the Potential Energy Surface of C₉H₉⁺ by ab Initio Methods. 2. Is the 1,4-Bishomotropylium Cation a Bishomoaromatic Prototype?. In: J. Am. Chem. Soc., 1993, 115, S. 7457–7464.
D. Cremer, F. Reichel, E. Kraka: Homotropenylium Cation: Structure, Stability, Magnetic Properties. In: J. Am. Chem. Soc., 1991, 113, S. 9459–9446.
R. Herges, H. Jiao, P. v. R. Schleyer: Magnetic Properties of Aromatic Transition States: The Diels-Alder Reactions. In: Angew. Chem. Int. Ed. Engl., 1994, 33, S. 1376–1378.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[DOI10.1351/pac199668020209-1] P. von Ragué-Schleyer, Haijun Jiao: What is aromaticity?. In: Pure and Applied Chemistry. 68, 1996, S. 209, doi:10.1351/pac199668020209.

[2] Eintrag zu aromaticity. In: IUPAC (Hrsg.): Compendium of Chemical Terminology. The “Gold Book”. doi:10.1351/goldbook.A00442 – Version: 2.3.3.

[DOI10.1021/ja01005a059-3] Hyp J. Dauben, James Dennis. Wilson, John L. Laity: Diamagnetic susceptibility exaltation as a criterion of aromaticity. In: Journal of the American Chemical Society. 90, 1968, S. 811, doi:10.1021/ja01005a059.

[DOI10.1021/ja00315a036-4] Michael J. S. Dewar: Chemical implications of σ conjugation. In: Journal of the American Chemical Society. 106, 1984, S. 669, doi:10.1021/ja00315a036.

[DOI10.1016/S0040-4020(01)86238-4-5] Dieter Cremer: Pros and cons of σ-aromaticity. In: Tetrahedron. 44, 1988, S. 7427, doi:10.1016/S0040-4020(01)86238-4.

[King-6] Z. Chen, R. B. King: Spherical Aromaticity: Recent Work on Fullerenes, Polyhedral Boranes, and Related Structures. In: Chem. Rev., 2005, 105, S. 3613–3642.

[7] Eine Übersicht der aktuellen Diskussion zum Thema Aromatizität und Antiaromatizität findet sich in Chemical Reviews Vol. 101, Heft 5, 2001 sowie Vol. 105, Heft 10, 2005.

[NICS-8] Z. Chen, C.S. Wannere, C. Corminboeuf, R. Puchta, P. v. R. Schleyer: Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion. In: Chemical Reviews, 2005, 105, S. 3842, doi:10.1021/cr030088+

[9] A. Kekulé: Sur la constitution des substances aromatique. In: Bull. Soc. Chim. Paris, 1865, 3, S. 98–111. pdf

[10] E. Erlenmeyer: Studien über die s. g. aromatischen Säuren. In: Ann., 1866, 137, S. 327–359.

[11] P. Pascal: Recherches Magnétochimiques. In: Ann. Chim. Phys., 1910, 19 (8), S. 5–70. pdf

[12] J. W. Armit, R. Robinson: CCXI.—Polynuclear heterocyclic aromatic types. Part II. Some anhydronium bases. In: J. Chem. Soc., Trans., 1925, 127, S. 1604–1618.

[13] E. Hückel: Quantentheoretische Beiträge zum Benzolproblem. In: Z. Physik, 1931, 70, 204–286 und 72, S. 310–337.

[14] L. Pauling: The Diamagnetic Anisotropy of Aromatic Molecules. In: J. Chem. Phys., 1936, 4, S. 673–677.

[15] F. London: Théorie quantique des courants interatomiques dans les combinaisons aromatiques. In: J. Phys. Radium 1937, 8, S. 397–409.

[16] J. A. Pople: Proton Magnetic Resonance of Hydrocarbons. In: J. Chem. Phys., 1956, 24, S. 1111.

[17] R. C. Benson, W. H. Flygare: Molecular Zeeman effect of cyclopentadiene and isoprene and comparison of the magnetic susceptibility anisotropies. In: J. Am. Chem. Soc., 1970, 92, S. 7523–7529.

[18] J. Aihara: Three-dimensional aromaticity of polyhedral boranes. In: J. Am. Chem. Soc., 1978, 100, S. 3339–3342.

[19] W. Kutzelnigg: Theory of Magnetic Susceptibilities and NMR Chemical Shifts in Terms of Localized Quantities. In: Isr. J. Chem., 1980, 19, S. 193–200.

[Schleyer_NICS-20] P. v. Ragué-Schleyer, C. Maerker, A. Dransfeld, H. Jiao, N. J. R. v. E. Hommes: Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. In: J. Am. Chem. Soc., 1996, 118, S. 6317–6318.

[21] K. Freitag, C. Gemel, P. Jarabek, I. M. Oppel, R. W. Seidel, G. Frenking, H. Banh, K. Dilchert, R. A. Fischer: The σ-Aromatic Clusters [Zn₃]⁺ and [Zn₂Cu]: Embryonic Brass. In: Angew. Chem. Int. Ed., 2015, 54, S. 4370–4374.

[22] R. V. Williams: Homoaromaticity. In: Chem. Rev., 2001, 101, S. 1185–1204.

[23] Z. Chen, R. B. King: Spherical Aromaticity: Recent Work on Fullerenes, Polyhedral Boranes, and Related Structures. In: Chem. Rev., 2005, 105, S. 3613–3642.

[24] J. D. Roberts, M. C. Caserio: Basic Principles of Organic Chemistry, W. A. Benjamin Inc., New York, Amsterdam, 1965.

[25] Alan R. Katritzky, Karl Jug, Daniela C. Oniciu: Quantitative Measures of Aromaticity for Mono-, Bi-, and Tricyclic Penta- and Hexaatomic Heteroaromatic Ring Systems and Their Interrelationships. In: Chem. Rev., 2001 101, S. 1421–1449, doi:10.1021/cr990327m und dort zitierte Literatur.

[Cyrański-26] Michał Ksawery Cyrański: Energetic Aspects of Cyclic Pi-Electron Delocalization: Evaluation of the Methods of Estimating Aromatic Stabilization Energies. In: Chem. Rev. 2005, 105, S. 3773–3811, doi:10.1021/cr0300845.

[27] Eintrag zu homodesmotic reaction. In: IUPAC (Hrsg.): Compendium of Chemical Terminology. The “Gold Book”. doi:10.1351/goldbook.HT07048 – Version: 2.3.3.

[28] Der Begriff "homodesmotisch" wird in der Literatur nicht immer einheitlich verwendet. Ein kritischer Kommentar und ein Vorschlag zur Vereinheitlichung findet sich in S. E. Wheeler, K. N. Houk, P. v. R. Schleyer, W. D. Allen: A Hierarchy of Homodesmotic Reactions for Thermochemistry. In: J. Am. Chem. Soc., 2009, 131, S. 2547–2560.

[29] Schleyer et al. in Chem. Rev., 2005, 105, S. 3842–3888 und dort zitierte Literatur.

[30] Die verwendete Reaktion wird von den Autoren zwar als homodesmotisch bezeichnet, erfüllt die Begriffsdefinition jedoch nicht, vgl. die Diskussion durch Cyrański in Chem. Rev., 2005, 105, S. 3773–3811.

[Schleyer_5_Ringe-31] P. v. Ragué-Schleyer, P. Freeman, H. Jiao, B. Goldfuss: Aromaticity and Antiaromaticity in Five-Membered C₄H₄X Ring Systems: “Classical” and “Magnetic” Concepts May Not Be “Orthogonal”. In: Angew. Chem. Int. Ed., 1995, 34, S. 337–340.

[32] Cyclopentadien wird von den Autoren als Grenzfall eines aromatischen Systems diskutiert, wobei die cyclische Delokalisation durch Einbeziehen von zwei Elektronen der CH2-Gruppe erreicht wird. Vgl. hierzu auch die im Artikel zitierte Literatur.

[DOI10.1021/cr990367q-33] Kenneth B. Wiberg: Antiaromaticity in Monocyclic Conjugated Carbon Rings. In: Chemical Reviews. 101, 2001, S. 1317, doi:10.1021/cr990367q.

[34] Moderne quantenchemische Rechenmethoden erlauben es heute, die magnetischen Eigenschaften von Molekülen zu berechnen. Derartige Methoden standen nicht zur Verfügung als das Kriterium der diamagnetischen Anisotropie zum Studium aromatischer Verbindungen eingeführt wurde.

[Cremer_bishomotropylium-35] D. Cremer, P. Svensson, E. Kraka, Z. Konkoli, P. Ahlberg: Exploration of the Potential Energy Surface of C₉H₉⁺ by ab Initio Methods. 2. Is the 1,4-Bishomotropylium Cation a Bishomoaromatic Prototype?. In: J. Am. Chem. Soc., 1993, 115, S. 7457–7464.

[Cremer_homotropylium-36] D. Cremer, F. Reichel, E. Kraka: Homotropenylium Cation: Structure, Stability, Magnetic Properties. In: J. Am. Chem. Soc., 1991, 113, S. 9459–9446.

[37] R. Herges, H. Jiao, P. v. R. Schleyer: Magnetic Properties of Aromatic Transition States: The Diels-Alder Reactions. In: Angew. Chem. Int. Ed. Engl., 1994, 33, S. 1376–1378.